某型航空发动机扭矩曲线故障原因分析与排故

丁 琪，邹 闰，马洪亮，唐家茂，陈蔚兴，罗 岸，韩奉林

（1.陆军装备部航空军事代表局驻株洲地区航空军事代表室，湖南 株洲 412002；2.中南大学机电工程学院，湖南 长沙 410012；3.中国航发南方工业有限公司，湖南 株洲 412002）

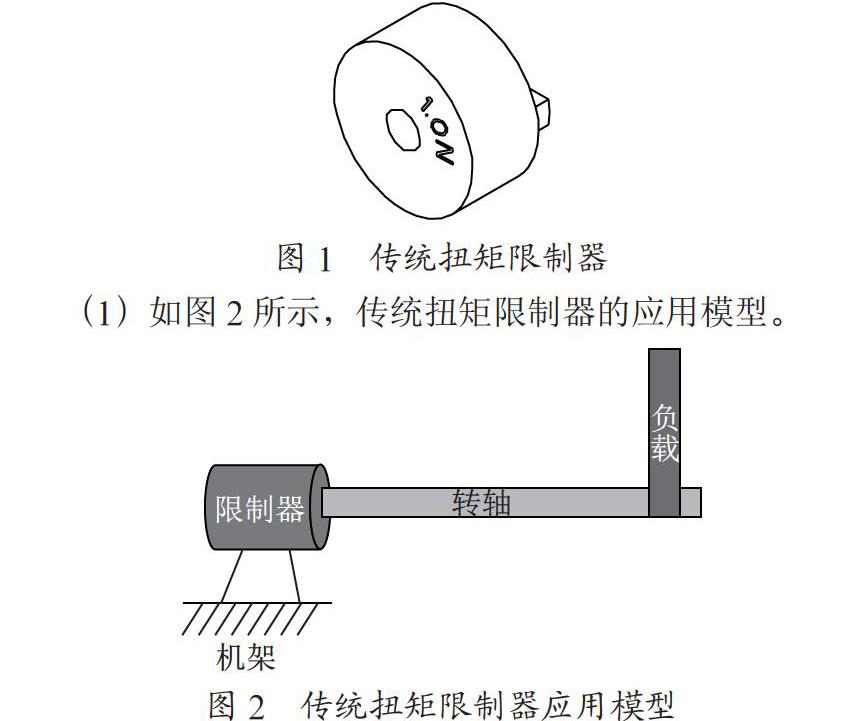
航空发动机是飞机飞行的直接动力来源，其中输出功率是发动机的基本参数之一，用于指示发动机工作状态，对保证飞机飞行安全有着重要作用。在某款航空发动机中，测扭结构位于减速单元体中，通过测量内部滑油压力间接获得发动机输出扭矩。在发动机生产出厂时，需对其进行试车，并绘制扭矩曲线。但在实际生产实践中，经常出现扭矩曲线不合格故障，且故障来源不明确，排故检修困难，严重影响了发动机交付进度，造成较大经济损失。

本文以某型航空发动机测扭机构为研究对象，对测量过程进行力学建模与分析，分析扭矩曲线故障产生的主要因素，分析不同温度下扭矩曲线故障的产生原因。并据此提出相应的工程改进措施。

在某款航空发动机中，测扭结构位于减速单元体中，如图1所示。减速器工作过程中，中间齿轮受到向左的轴向力（由主动齿轮和输出齿轮共同作用），轴向力的大小与发动机的功率近似成正比，并通过三联轴承传递到测扭柱塞上。滑油经调节压力进入柱塞腔，向右推动柱塞，在测量过程中，柱塞在左端油压及斜齿轮轴向力作用下动态平衡，通过测量柱塞腔中滑油压力即可实时测量真实输出扭矩。

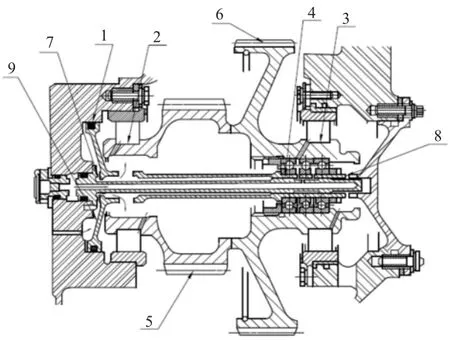
图1 测扭机构

在对发动机进行试车时，通过水力测功机对输出扭矩进行测量，并控制润滑油温度为60℃和90℃，滑 油 压 力 为100 kPa、150 kPa、200 kPa、250 kPa、300 kPa和350 kPa时，记录滑油压力与输出扭矩值，并绘制扭矩特性曲线图，如下页图2所示。要求两条曲线在上下控制线内，并且偏差不超过10 N·m。在发动机进行试车时，扭矩曲线的主要故障情况为两条曲线超差，故障发动机需下车排故，严重影响了发动机交付进度。

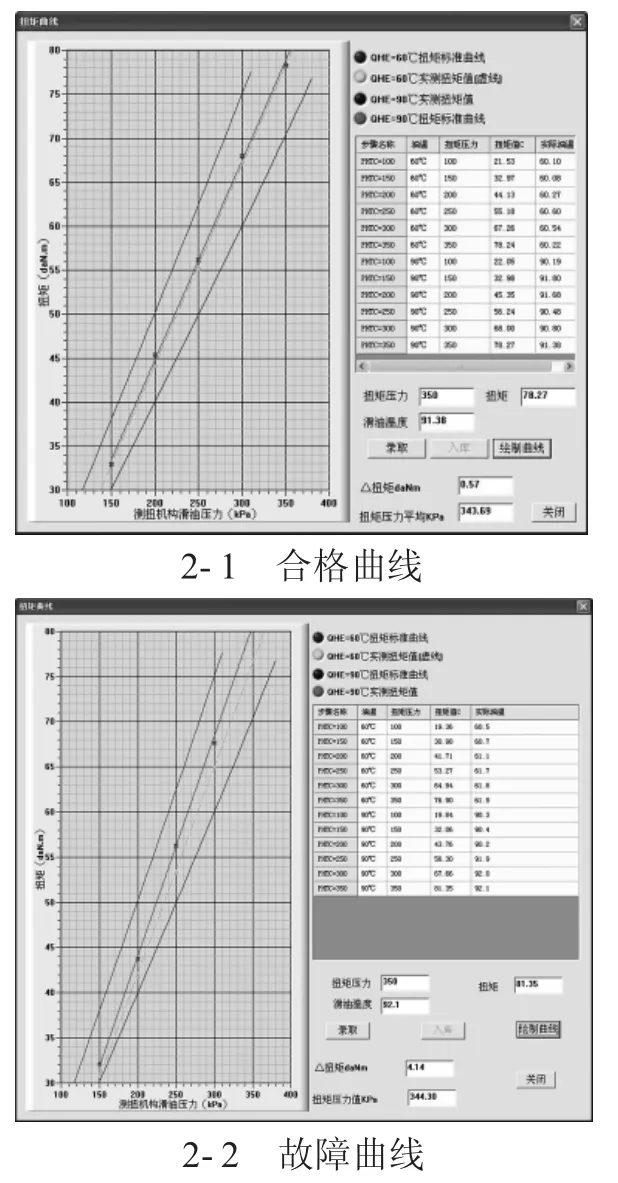
图2 扭矩曲线

由于扭矩曲线线性度较好，因此，可将扭矩曲线模型简化为T=kP+b形式的线性模型，忽略分段函数、高次函数等，扭矩T关于滑油压力P的非线性项。基于此简化原则，可忽略以下非线性因素：

1）柱塞组件与润滑导管之间的间断性碰摩。

2）中间齿轮及其他零件的受力变形。

3）各运动副之间的非线性摩擦力（考虑线性摩擦）。

4）各运动件的振动等动力学效应。

将柱塞、中间齿轮和三联轴承视为一个整体，对柱塞轴向载荷产生影响的因素主要包括以下方面。

2.2.1 齿轮啮合

减速单元体为两级斜齿轮减速，在斜齿轮啮合过程中，影响柱塞轴向受力的主要有中间齿轮所受的轴向分力Fa和沿齿面切向的摩擦力。Fa如式（1）所示：

式中：Tg为中间齿轮传递的扭矩，N·m；d1、d2为大、小齿轮的实际啮合半径，mm；β1、β2为大、小齿轮的螺旋角。

由于轮齿在开始啮合到完全脱开这一周期内，沿齿面切向的滑移摩擦力在轴向分力方向会发生变化。在一个周期内，滑移摩擦力对柱塞的冲量积分为零，并且齿轮啮合频率较高，因此，齿面摩擦力并不会影响柱塞稳定的轴向受力。

2.2.2 滑油压力

在测量过程中，柱塞处于动态平衡状态。泄油口处虽有滑油流出，但泄油量较小，因此，可将油腔内滑油压力视为静压。

滑油压力对柱塞的轴向力F0为：

式中：p为滑油压力，kPa；A为油腔截面积，mm2。

2.2.3 中间轴承的轴向摩擦力

中间齿轮前后轴承处于弹流润滑状态，其摩擦阻力Fb较为复杂。但根据模型假设，可将其简化为Fb=μN形式，因此，前后轴承对柱塞的轴向阻力为：

式中：μb为轴承润滑油膜的摩擦系数；R1、R2为前后轴承支反力，N。

2.2.4 柱塞与油腔之间的摩擦力

柱塞与油腔间摩擦力与载荷无关，主要受衬套与油腔之间配合关系的影响。因此，在柱塞整体受力模型中，柱塞与油膜之间的摩擦力可以认为是独立于载荷的常数，主要影响模型常数项。柱塞与油腔之间的摩擦力Fp为：

式中：μp为衬套与油腔之间的摩擦系数；Np为柱塞与油腔之间正压力，N。

2.2.5 柱塞与润滑导管之间的阻力

柱塞与润滑导管间阻力的存在取决于中间齿轮轴系安装质量。当两者处于接触状态时，中间齿轮处于静不定结构状态，两者间的正压力难以直接求得。但此正压力与载荷呈正相关，根据历史数据分析得到的线性结果，可假设正压力Nl为：

式中：kl为与中间齿轮轴系安装质量相关的系数。柱塞与润滑导管之间的阻力Fl为：

式中：μl为阻塞与润滑导管之间的摩擦系数。

2.2.6 中间齿轮传递扭矩与测功机示值之间的关系

发动机试车采用水力测功机测量，Po为输出功率，no为输出转速，To为输出扭矩。

结合中间齿轮与输出齿轮减速比以及传动系统的效率βo，可得到中间齿轮传递扭矩Tg与测量输出扭矩To的关系，如下式所示：

基于对柱塞的受力分析，可以建立起单元体扭矩测量模型。由于在进行数据采集时柱塞运动状态未知，因此，在理论上无法判断摩擦阻力方向。按照阻塞组件的运动状态或运动趋势，可将模型分为三种情况。

2.3.1 柱塞向左运动

由受力平衡，有：

代入表达式，并整理：

2.3.2 柱塞向右运动

同理，由受力平衡有：

代入具体表达式并整理后有：

2.3.3 柱塞静止状态

当柱塞处于静止状态时，上述摩擦力大小均无法确定，因此将Fb、Fp、Fl合并记为Ff，Ff的方向取决于代入具体表达式并整理后有：

因此，可获得调制滑油压力与输出扭矩的总体模型：

从上述力学模型可知，前后轴承的轴向摩擦力是影响T-P曲线斜率的重要因素，受轴承微观表面及润滑状态的影响，处于典型的弹流润滑状态。弹流润滑受润滑油黏度的影响，因此，轴承滚子与滚道间润滑油膜的润滑性能随温度变化，符合扭矩曲线在不同温度下轴承斜率发生变化的实际情况。

19世纪初，Stribeck通过对径向推力轴承进行研究，提出了着名的Stribeck曲线[1]，如图3所示。从图中可以看出，当润滑状态处于全膜润滑状态时，摩擦系数很小且较稳定。处于边界润滑状态时，摩擦系数较大但变化不大。但处于混合润滑状态时，摩擦系数会发生突变。因此，需计算中间齿轮前后轴承的最小油膜厚度，判断摩擦系数是否为影响扭矩测量的主要因素。

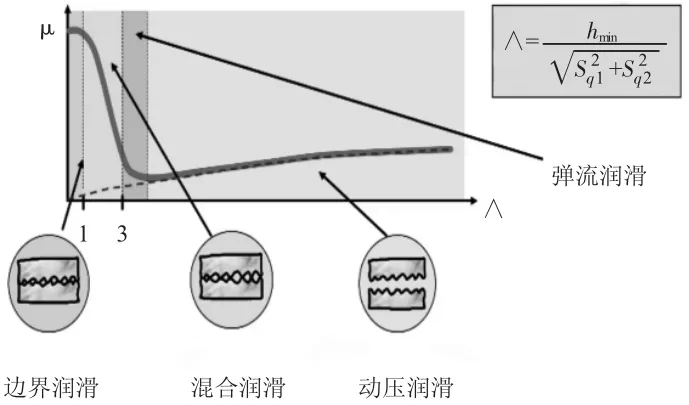
图3 润滑状态分类

中间轴承为圆柱滚子轴承，为典型的线接触弹流润滑状态，许多研究者针对线接触弹流润滑方程进行了研究，建立了用于估算最小油膜厚度hmin的方程，其中应用较为广泛的是Hamrock-Dowson公式[2]：

式中：η0为润滑油动力黏度，N·s/m2；R为当量柱体半径，m；E” 为综合弹性模量，为单位接触长度上的最大载荷，为平均搅油速度，为润滑油黏压系数，

Hamrock-Dowson公式应用于等温、光滑表面，分别代入60℃和90℃时润滑油的动力黏度进行计算，可得滚动体与轴颈、滚动体与外圈间在不同温度下的最小油膜厚度，如表1所示。

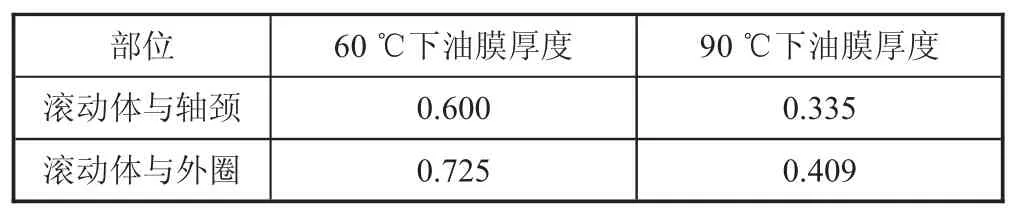
表1 最小油膜厚度 μm

从Stribeck曲线可以看出，比油膜厚度∧是判断润滑状态的重要参数，其计算公式如下：

式中：sq1、sq2为轮廓的均方根偏差，μm。代入最小油膜厚度以及相关部位表面粗糙度，可得滚动体与轴颈、滚动体与外圈间在不同温度下的∧值，如表2所示。

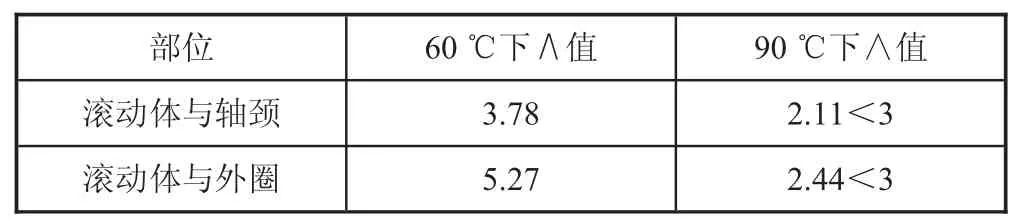
表2 比油膜厚度

可以看出，在60℃时，内外圈比油膜厚度＞3，处于全膜润滑状态。而在90℃时，内外圈比油膜厚度＜3，处于混合摩擦状态。在此状态下，系统摩擦系数会出现较大的突变，对扭矩数据的稳定测量造成较大的影响。

在60℃时，内外圈均处于全膜润滑状态，摩擦系数极低且稳定。但在90℃时，由于润滑油黏度降低，最小油膜厚度也随之减小，轴承内外圈处于混合摩擦状态，摩擦系数明显升高且不稳定。同时结合力学建模方程可以看出，90℃时摩擦系数增大将导致扭矩曲线斜率产生偏移，使扭矩曲线远离正常润滑时扭矩曲线，造成曲线超差故障。

针对此故障原因，需严格控制中间齿轮前后轴承内跑道的表面粗糙度，将工况数据代入Hamrock-Dowson公式中，可以得到滚子与外圈之间60℃下中间齿轮的油膜厚度为0.606 μm。90℃下中间齿轮的最小油膜厚度为0.342 μm。为达到全膜润滑，比油膜厚度需要达到3以上。因此，滚子与外圈跑道间的综合表面均方根偏差不能大于0.085 5 μm（∧=4）。当前技术水平下，滚子的表面粗糙度一般在Ra0.05 μm。因此，需要将中间齿轮前后轴承内跑道的表面粗糙度控制在Ra0.07 μm以下。

表3为措施实施前后故障率对比，可以看出，将改进措施应用于实际生产后，扭矩曲线故障率相比实施前有了很大的改善。

表3 故障率统计

基于测扭原理建立测扭机构力学模型，分析滑油压力与输出扭矩的总体模型，可知中间轴承在工作时的摩擦系数对扭矩测量有着重要影响。为此，通过计算中间轴承最小油膜厚度和比油膜厚度对轴承润滑状态进行了评判，结果表明，90℃时比油膜厚度∧＜3，轴承处于混合摩擦状态，摩擦系数较大且不稳定，对扭矩曲线的测量有着较大的影响。针对故障原因，提出了将中间齿轮前后轴承内跑道的表面粗糙度控制在Ra0.07 μm以下的解决措施，并通过试车验证。实践证明，采取此措施后，大大减小了由发动机下车、拆解、返修、重新装配带来的时间和经济上的损失，效果显着。