李志刚,秦林林,孙 婷
(1.华北理工大学人工智能学院,河北 唐山 063210;2.河北省工业智能感知重点实验室,河北 唐山 063210)
引言构建合理的空气质量数据分析与预测模型对我国经济发展具有重要意义。一般情况下,PM2.5被视为我国大部分地区的最重要的大气污染物之一,且受到时空尺度的影响[1-2]。因此,本文重点关注多站点协同下的PM2.5分析与建模问题,进而构建了TS-TDBN-ELM模型。
1 理论基础1.1 CRQA分析CRQA能够探究两个非线性信号间相似动力学行为[3]。首先,将两组空气质量数据重构至高维相空间,观察其在相空间中的运动轨迹距离。然后,采用递归率(Recurrence Rate,RR)、确定性(Determinism,DET)、层流性(Laminarity,LAM)和平均对角线长度(Mean Diagonal length,MDL)四个指标对二者之间的动力学特性进行定量测度,筛选出影响PM2.5的主要因素,作为后续预测模型的输入。
1.2 TDBN-ELM模型此部分采用DBN-ELM模型对PM2.5进行多输入单输出预测。其中,采用DBN对CRQA筛选出的因素进行关键特征提取,将提取后的数据特征输入ELM中,完成最终PM2.5预测。为进一步提升预测性能,引入了TLBO算法,对DBN-ELM中各个隐藏层神经元的学习率进行优化。
2 实验仿真2.1 数据来源与评估指标实验选取目标站点天坛(Tiantan,TT)、临近站点万寿西宫(Wangshouxi,WSX)与临近站点官园(Guanyuan,GY)[4]。数据包含12种因素,分别为PM2.5、PM10、SO2、NO2、CO、O3、温 度(Temperature,T)、气 压(Pressure,P)、露点温度(Dew Point Temperature,DT)、雨量(Rain,R)、风向(Wind Direction,WD)与风速(Wind Speed,WS)。为验证模型的有效性,采用归一化均方根误差(Normalized Root Mean Squared Error,NRMSE)、平均绝对误差(Mean Absolute Error,MAE)、决定系数(Coefficient of Determination,CD)评估模型性能。
2.2 CRQA分析下页表1给出了多站点中因素对TTPM2.5的相似性度量指标值,与TTPM2.5相似性最强的因素已加粗显示。RR值越高,表明当前因素与TTPM2.5出现的相似性概率越高。可以看到,在该指标下,三个站点中的R与TTPM2.5间相似性最强。DET越高,表明各个因素与TTPM2.5之间相似动态的确定性越强。由下页表1可知,T与TTPM2.5间相似状态具有更高的规律性和可预测性。LAM度量了PM2.5与各个影响因素之间的同步性,其值越高,表示运动状态的同步时间就越长。在三个站点中,CO、T、T分别与TTPM2.5之间的同步性最高。MDL是度量不同因素与PM2.5之间相似性的重要指标。可以看到R、T与TTPM2.5保持着较高的相似性。综合四种指标,确定影响TTPM2.5的主要因素,分别为TT,SO2、CO、T、P、DT与R;WSX,O3、T、DT与R;GY,CO、T、DT与R。上述因素与TTPM2.5共同作为预测模型输入。
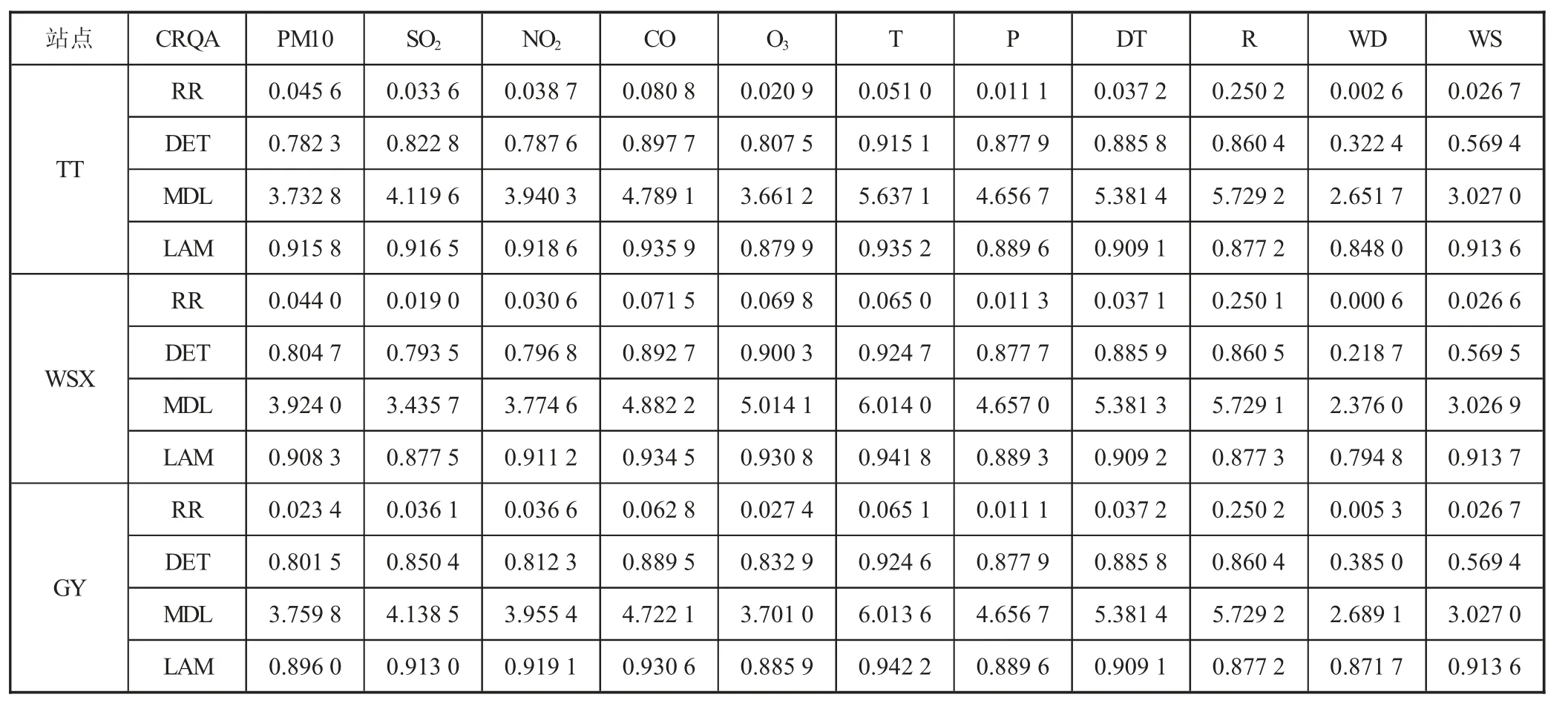
表1 TT中PM2.5与其他站点其他影响因素CRQA测度
下页图1给出了时空尺度下基于PM2.5序列的预测曲线与实际曲线对比结果。可以看出,SVM与ELM模型的PM2.5预测曲线与实际PM2.5曲线的拟合度较差。从下页图1可以看到,DBN-ELM与TS-TDBN-ELM模型在相应时间步上的PM2.5预测曲线与实际PM2.5曲线的变化趋势较为一致。下页表2给出了时空尺度下多种模型的预测性能对比结果。由下页表2可得,TS-TDBN-ELM预测算法的NRMSE、MAE指标的值分别为0.2436、0.0146,这比其他五种对比模型相应误差指标值更小,即该模型预测所得PM2.5与实际PM2.5间的偏差更小、精度更高。此外,还可以看出,TS-TDBN-ELM预测模型的CD值为0.9963,这说明该模型具有良好的非线性拟合能力。
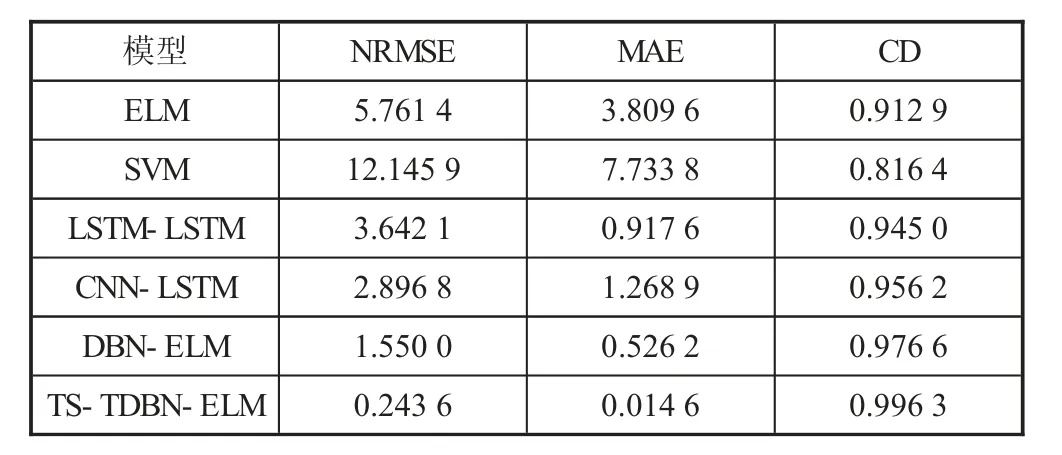
表2 预测模型相应评估指标值对比
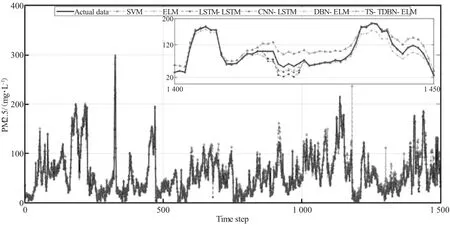
图1 模型预测PM2.5曲线与实际PM2.5曲线对比
3 结论提出了一种多站点协同PM2.5的预测架构TSTDBN-ELM,主要包含CRQA分析与TDBN-ELM预测组成。其中,CRQA能够挖掘多站点模式下多种因素与目标站点PM2.5的动态相关性,确定影响PM2.5的主要因素,为后续预测提供优质输入条件。在预测部分,采用TLBO优化DBN-ELM各隐层神经元学习率,进一步提升了它的预测性能。实验结果表明,TS-TDBN-ELM具有最优的预测性能。