摘 要:本文以长江经济带中游地区的三大港口城市——武汉市、九江市和岳阳市为研究对象,基于其港口物流数据,运用平稳性检验、协整分析等方法,构建向量误差修正模型(VECM),并结合格兰杰因果检验和脉冲响应分析,深入探究港口货物吞吐量、集装箱吞吐量与区域经济增长(以GDP衡量)之间的动态关联,旨在实证分析港口物流活动与区域经济增长之间的长期均衡关系。研究结果表明,港口物流活动与区域经济增长之间存在长期均衡关系和动态因果关系,其对区域经济增长的影响较为显著,从长期来看,港口物流活动对区域经济增长具有正向推动作用。
关键词:港口物流;区域经济;协整分析;VECM 模型;格兰杰因果检验
中图分类号:F592.7 文献标识码:A 文章编号:2096-0298(2025)05(a)--04
1 引言
长江中游城市群作为长江经济带的重要组成部分,具有承东启西、连接南北的独特区位优势,是我国区域经济发展的重要战略支点[1]。近年来,随着《长江中游城市群发展规划》深入实施,推动长江中游城市群的经济发展已成为国家区域发展战略的重要方向。在此背景下,分析长江中游城市群与港口之间的联系、深入探讨港口城市群的物流活动与区域经济增长的驱动机制,对进一步优化当地区域经济布局和提升当地经济竞争力具有重要的现实意义。
本文选择协整理论(Engle amp; Granger, 1987)、向量误差修正模型(Johansen, 1991)[2]和VECM模型[3],对长江中游地区的岳阳、九江和武汉三座港口城市展开研究。这三座城市分别位于湖南、江西和湖北,代表了长江中游地区不同省份的港口经济发展模式,能够为研究提供多样化的数据支持,而且三座城市的港口数据相对完整且易于获取,确保了研究的科学性与可靠性,有助于更全面地揭示港口物流与区域经济增长的关系。
2 理论基础、研究设计与数据来源
2.1 理论基础
2.1.1 经济增长理论[4]
经济增长理论是研究经济增长动因及其影响机制的核心理论框架。该理论着重强调生产要素的积累及配置效率对经济增长的关键驱动作用。港口物流活动借助贸易促进效应、资源配置优化等途径,对区域经济增长产生深刻影响。具体而言,港口物流活动能够通过以下几点推动经济增长:
贸易促进效应:港口作为国际贸易的重要节点,其物流活动能够显著提升区域与外部经济体的贸易规模,从而增强区域经济的开放性和竞争力。
资源配置优化:港口物流活动通过高效的运输和仓储体系,能够降低生产要素的流动成本,提升资源配置效率,促进区域经济集约化发展。
2.1.2 新经济地理学理论[5]
新经济地理学理论关注地理位置、空间集聚和经济增长之间的关系。该理论指出,区域之间的交通基础设施及物流活动对产业集聚、区域经济增长具有显著影响[6]。其核心观点如下:
交通基础设施的集聚效应:港口作为重要的交通基础设施,能够吸引相关产业在周边区域集聚,形成产业集群,提升区域经济的规模效应和竞争力。
区域经济联系的强化和空间溢出效应:港口物流活动能够加强区域间的经济联系,促进区域间的分工与合作,能通过空间溢出效应推动区域经济一体化发展。
2.2 研究设计与数据来源
2.2.1 基于上述理论基础,本文提出以下两个研究假设:
假设1:基于经济增长理论,三座城市港口的货物吞吐量、集装箱吞吐量与区域经济增长之间存在长期均衡关系。
假设2:基于新经济地理学理论,港口物流活动与区域经济增长之间具有显著的动态因果关系。
2.2.2 数据来源与变量选择
本文选取2002—2023年武汉市、九江市和岳阳市的港口货物吞吐量(万吨)、集装箱吞吐量(万TEU)和GDP(亿元)作为研究对象。数据来源于《武汉市统计年鉴》《九江市统计年鉴》《岳阳市统计年鉴》和数据汇聚网站。为消除数据的异方差性,本文对所有变量均取自然对数处理。
2.2.3 对数据进行平稳性检验
时间序列分析要求数据平稳,否则可能导致伪回归问题。本文采用ADF检验方法对各变量的平稳性进行检验。ADF检验的基本原理是通过检验时间序列的单位根判断其平稳性——如果时间序列存在单位根,则该序列是非平稳的。
2.2.4 对数据进行协整分析
协整分析用于判断非平稳时间序列之间是否存在长期均衡关系,要求所有变量必须是同阶单整。本文采用Johansen协整检验方法,基本原理是通过检验变量之间的协整秩来判断是否存在协整关系——如果协整秩大于零,则说明变量之间存在长期均衡关系。具体公式如下:
ΔYt=∏Yt-1+Γ1ΔYt-1+…+Γk-1ΔYt-(k-1)+εt
其中,Yt是包含港口货物吞吐量、集装箱吞吐量和GDP的向量,Δ是差分算子,∏是协整矩阵,Γi是短期参数矩阵,k是滞后阶数,εt是误差项。同时,协整矩阵∏可以进一步分解为:
∏=αβT
其中,α是调整参数矩阵,β是协整向量矩阵。Johansen检验通过特征值和迹统计量确定协整关系的数量,即β的秩。
迹统计量(Trace Statistic)用于检验至少存在r个协整关系,其计算公式为:
Trace Statistic=
其中,T是样本容量,n是变量的个数,是特征值。
最大特征值统计量(Max-Eigen Statistic)用于检验恰好存在r个协整关系,公式为:Max-Eigen Statistic=-Tln ln(1-)
这些统计量会与相关的临界值进行比较,从而判断协整关系的存在性和数量。
2.2.5 向量误差修正模型(VECM)
当变量之间存在协整关系时,可以构建向量误差修正模型(VECM),分析变量之间的短期动态调整机制。VECM模型的基本形式为:
其中,Yt为变量向量,α和β分别为调整参数和协整向量,Γi为短期动态参数,εt为误差项。VECM模型能够同时捕捉变量之间的长期均衡关系和短期动态调整机制。
2.2.6 格兰杰因果检验
格兰杰因果检验用于判断变量之间的因果关系。在VECM框架下,格兰杰因果检验通过对差分序列进行回归分析,判断变量之间是否存在因果关系——如果滞后项的系数显著,则说明存在格兰杰因果关系。
3 实证结果分析
3.1 平稳性检验
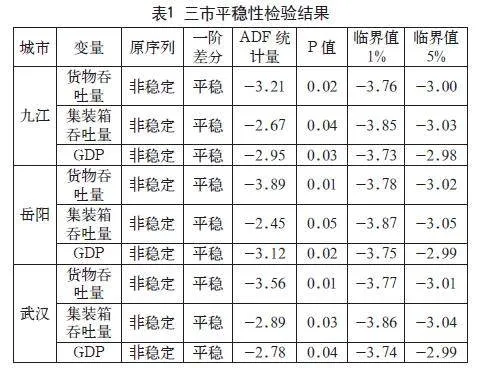
本文首先对九江市、岳阳市和武汉市的港口货物吞吐量、集装箱吞吐量及其GDP进行ADF检验。检验结果显示,各变量在经过一阶或二阶差分后均达到平稳状态。具体结果如表1所示。
以上平稳性检验结果表明,三市的货物吞吐量、集装箱吞吐量和其GDP在一阶差分后都是平稳的。因此,本文采用协整分析和VECM模型进一步分析可能存在协整关系的变量。
3.2 协整分析
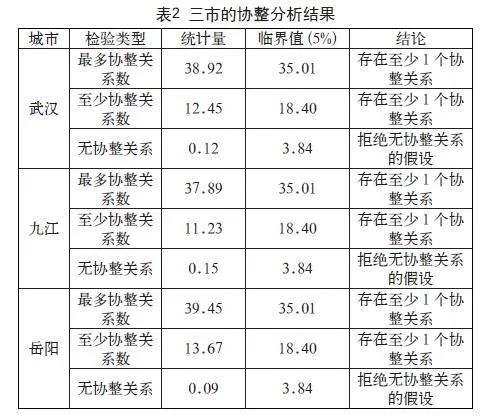
本文采用Johansen协整检验分析港口货物吞吐量、集装箱吞吐量与GDP之间的长期均衡关系。检验结果显示,变量之间存在协整关系,协整秩为1。具体结果如表2所示。
3.3 VECM模型构建
基于协整分析结果,本文构建向量误差修正模型(VECM),VECM模型的误差修正项反映了变量偏离长期均衡的调整速度。结合模型的长期弹性系数,协整方程结果如下:
(1)武汉市: GDP=7.87/12.34⋅货物吞吐量+4.21/12.34⋅集装箱吞吐量+ECM
标准方程:GDP=0.638⋅货物吞吐量+0.341⋅集装箱吞吐量+ECM(2=0.917)
(2)九江市: GDP=6.121/1.23⋅货物吞吐量+3.15/11.23⋅集装箱吞吐量+ECM
标准方程:GDP=0.545⋅货物吞吐量+0.281⋅集装箱吞吐量+ECM(2=0.885)
(3)岳阳市: GDP=7.36/13.56⋅货物吞吐量+4.13/13.56⋅集装箱吞吐量+ECM
标准方程:GDP=0.543⋅货物吞吐量+0.305⋅集装箱吞吐量+ECM(2=0.902)
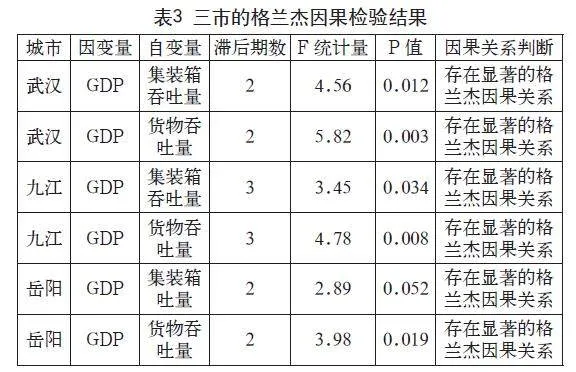
3.4 格兰杰因果检验
在VECM模型的基础上,本文对港口货物吞吐量、集装箱吞吐量与GDP之间的格兰杰因果关系进行了检验。检验结果显示,三个城市集装箱吞吐量和货物吞吐量对GDP存在显著的格兰杰因果关系。具体结果如表3所示。
3.5 脉冲响应和方差分解
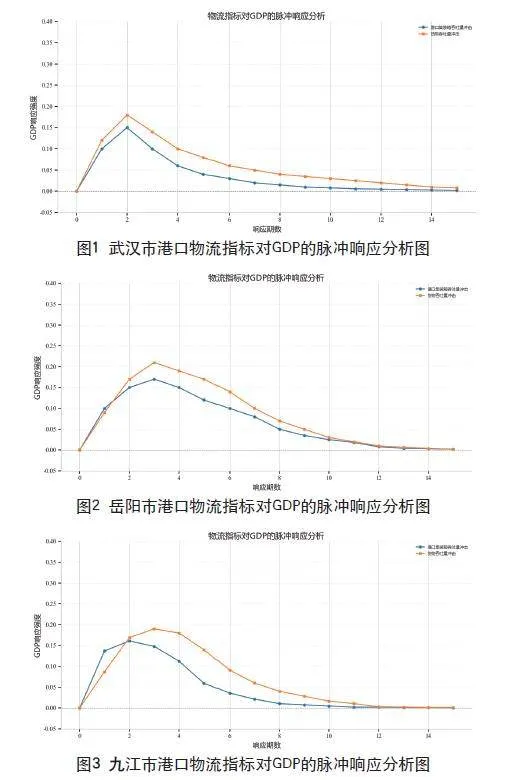
3.5.1 武汉市脉冲响应特征
货物吞吐量冲击:GDP在第1期出现正向响应(1.2%),第2期达到峰值(1.8%),随后缓慢衰减,至第10期仍保持0.4%的持续影响。
集装箱吞吐量冲击:响应滞后1期,第2期达到峰值(1.5%),衰减速度略快于货物吞吐量,反映集装箱运输对高附加值产业的短期促进作用更明显,长期需配套产业升级支撑。
3.5.2 岳阳市脉冲响应特征
货物吞吐量冲击:响应周期短且波动剧烈,第3期峰值高达2.1%,但第10期后迅速衰减至0.3%,揭示其对基建投资的高度依赖特征。
集装箱吞吐量冲击:响应曲线与货物吞吐量同步,第3期峰值1.7%,第10期衰减至0.25%,说明集装箱业务可能尚未形成独立产业生态。
货物吞吐量冲击:GDP在第2期响应达到(1.7%),第3期达到峰值(1.9%),但第10期后衰减至(0.2%)。
集装箱吞吐量冲击:呈现典型“陡升缓降”模式,第2期快速冲高至1.6%峰值,衰减周期短于货物吞吐量。
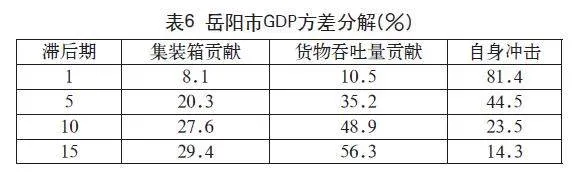
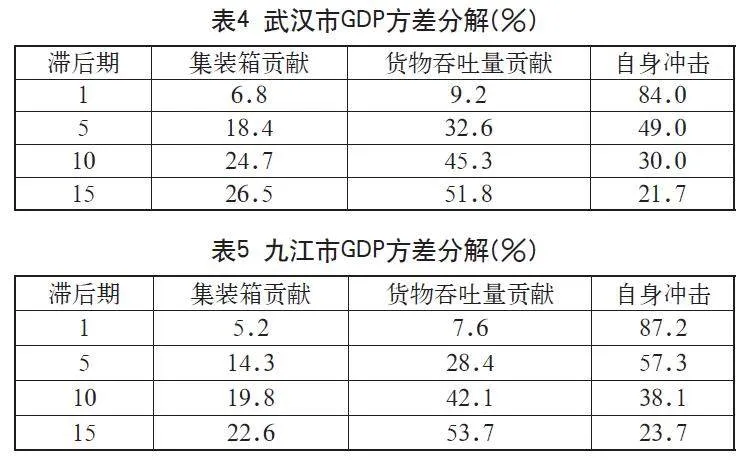
本研究通过方差分解方法对武汉、九江、岳阳三市的经济发展驱动力进行动态比较分析,揭示出不同时间维度下区域经济增长动力机制的差异化特征。实证结果如表4至表6所示。
在短期经济波动(1-5预测期)中,三市GDP变动的方差分解结果显示区域经济内生增长机制的初始主导性,其解释度分别为武汉市(84%-49%)、九江市(87.2%-57.3%)、岳阳市(81.4%-44.5%)。该动态演变趋势揭示出区域经济系统具有显著的内生增长惯性,特别是在经济冲击的初始传导阶段;相较之下,在长期经济演进(10-15预测期)过程中,港口物流要素的贡献率呈现显著上升趋势。其中,货物吞吐量对区域经济发展的贡献占比超越集装箱吞吐量,具体表现为:武汉市(集装箱26.5%,货物51.8%)、九江市(集装箱22.6%,货物53.7%)、岳阳市(集装箱29.4%,货物56.3%)的差异化贡献格局,该验证出货物吞吐量对经济结构升级的长期驱动作用。
4 结论与对策建议
4.1 主要结论
研究结果表明,港口货物吞吐量与集装箱吞吐量均与区域GDP存在长期均衡关系,其中货物吞吐量对经济增长的推动作用更为显著。在动态因果关系中,货物吞吐量和集装箱吞吐量均与区域GDP之间存在显著的格兰杰因果关系。故优化货物吞吐量,能够有效促进区域经济增长,为区域经济高质量发展提供重要动力。同时,本研究仍存在一定局限性。一是,研究范围仅限于三市,样本数据单一可能影响结论的普适性。二是,研究未深入探讨港口物流活动对区域经济增长的具体作用机制,以及港物流活动的空间溢出效应。未来的研究可从以下几点进一步拓展:一是通过面板数据分析多个港口城市的数据,验证本文结论的普遍性;二是结合空间计量经济学方法,深入分析港口物流活动对区域经济的空间溢出效应;三是进一步探讨港口物流活动对区域经济增长的作用机制,为区域经济政策的精准制定提供更全面的理论依据。
4.2 对策建议
4.2.1 优化集装箱运输效率
(1)加大港口基础设施投入,引入先进的装卸设备与技术,提升装卸能力,缩短船舶在港停留时间。在优化物流服务流程中,构建智能化管理系统,实现货物信息实时跟踪与精准调度,提升物流服务水平。
(2)强化多式联运协同合作,进一步提高集装箱运输效率。
4.2.2 加强区域经济合作
(1)建立区域经济合作机制,优化资源配置,明确各方在产业布局、基础设施建设、市场准入等方面的权责与分工,推动港城协同发展。
(2)加强交通基础设施互联互通,构建高效便捷的区域交通网络,降低物流成本,提升区域经济运行效率;通过举办区域经济合作论坛、产业对接会等活动,促进区域内企业交流合作,推动产业协同发展。
4.2.3 推动产业升级
(1)加大物流技术创新投入,鼓励企业应用大数据、人工智能等技术提升物流智能化水平。
(2)加强产学研合作,构建协同创新机制,为产业升级提供技术支持与人才保障。同时,注重绿色物流发展,推动企业采用节能环保技术与设备,实现经济发展与环境保护的良性互动。
参考文献
贯彻落实长江经济带重大国家战略的重要举措: 国家发展改革委地区经济司负责人解读《长江中游城市群发展规划》[J].中国经贸导刊,2015(13):31-35.
孟魁,李成标,张晨.港口物流、产业结构与城市经济发展: 基于长江经济带的实证[J].统计与决策,2023,39(23):123-127.
黄承锋,雷洋,吴园.基于协整理论的内河航运发展与区域经济增长关系的实证分析[J].水运工程,2011(6):106-111.
邢志豪.国际贸易和经济增长理论在“一带一路”背景下的应用: 基于中国西部地区区域经济发展的分析[J].产业创新研究,2024(19):39-41.
范晓莉.数字金融发展、区域基础设施与地区经济增长: 基于新经济地理学视角的分析[J].西南民族大学学报(人文社会科学版),2023,44(9):94-103.
李俊,黄梅雪,杨瑞麒.产教融合型城市发展与建设的机制分析: 基于经济地理学的视角[J].教育发展研究,2024,44(5):70-76.

