黄勇超,邓发云
(广州南洋理工职业学院 智能工程学院,广东 广州 510900)
0 引 言Multisim是美国国家仪器NI公司推出的电子仿真与设计专业软件,利用虚拟信号、器件和仪器分析电路的动态过程十分方便。MATLAB是美国MathWorks公司出品的数学软件,集成数值分析、矩阵计算、科学数据可视化及非线性动态系统的建模和仿真,为科学研究、工程设计以及数值计算提供了全面的解决方案。
本文通过二阶运放电路实现控制理论中的二阶系统,用Multisim进行时域和频域仿真,并用MATLAB数值运算对二阶系统进行时域和频域分析,最后将MATLAB数值运算与Multisim仿真比较,找出各自的特点。
1 二阶系统中的数学模型建立一个二阶系统的数学模型如图1所示。
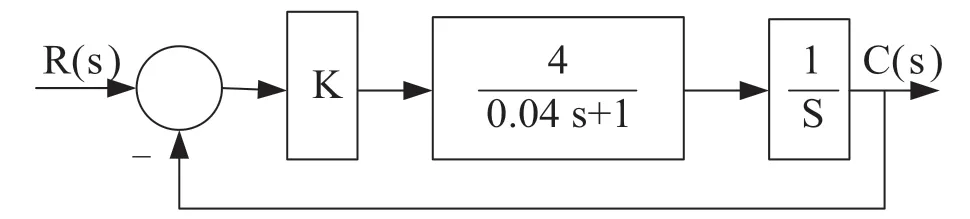
图1 二阶系统的数学模型

二阶系统的标准传递函数为:
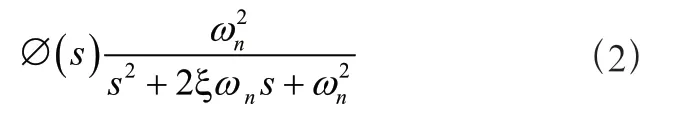
(2)式与(1)式对比,可求得阻尼比:
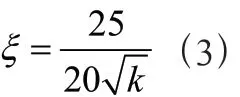
由(3)式可知,越小,二阶系统的阻尼比越大。当增益小于、等于、大于1.562 5时,二阶系统分别处于过阻尼、临界阻尼、欠阻尼状态;当增益→∞时,→0,二阶系统处于零阻尼状态。
2 二阶电路在Multisim中建模将图1所示二阶系统各控制环节进行转换,得到如图2所示的二阶运放电路。图中,直流电源提供1 V阶跃电压,运放U及各支路电阻构成比例环节,运放U及阻容构成惯性环节,运放U及阻容构成积分环节,运放U及电阻构成反相环节,反馈线从U引出形成电压并联负反馈,示波器观察输入输出信号。
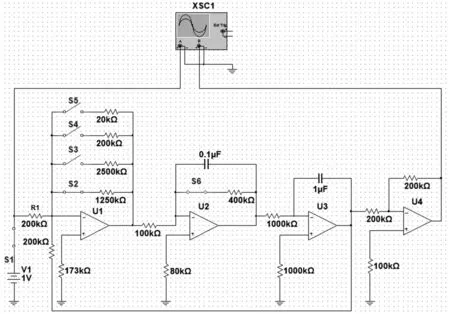
图2 二阶运放电路
3 二阶电路与二阶系统的时域仿真3.1 二阶电路时域的multisim仿真用multisim对二阶电路进行时域仿真,二阶无阻尼及过阻尼电路的时域响应曲线如图3所示。图2中,开关s6断开,开关s2~s5任一支接通,惯性环节变成积分环节,二阶电路特征方程无一次项,然后开关s1接通分别得到类似于图3(a)所示的二阶无阻尼电路响应曲线,电路处于不稳定状态。开关s4、s6接通,然后开关s1接通得到比例环节=1的二阶过阻尼电路单位阶跃响应曲线如图3(b)所示;开关s5、s6接通,然后开关s1接通得到比例环节=0.1的二阶过阻尼电路单位阶跃响应曲线如图3(c)所示。可见,二阶过阻尼电路增益越小,则阻尼比越大,调节时间越长。
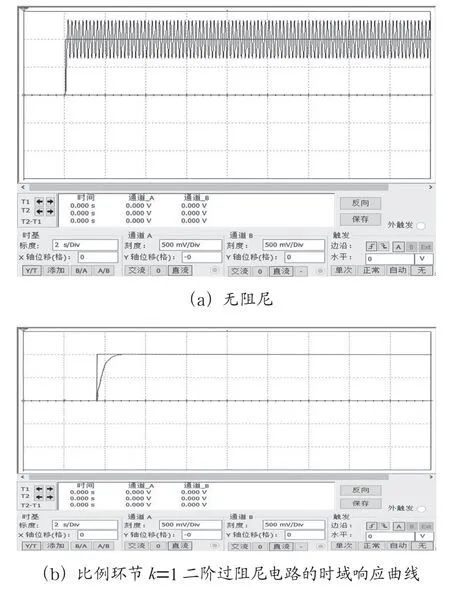
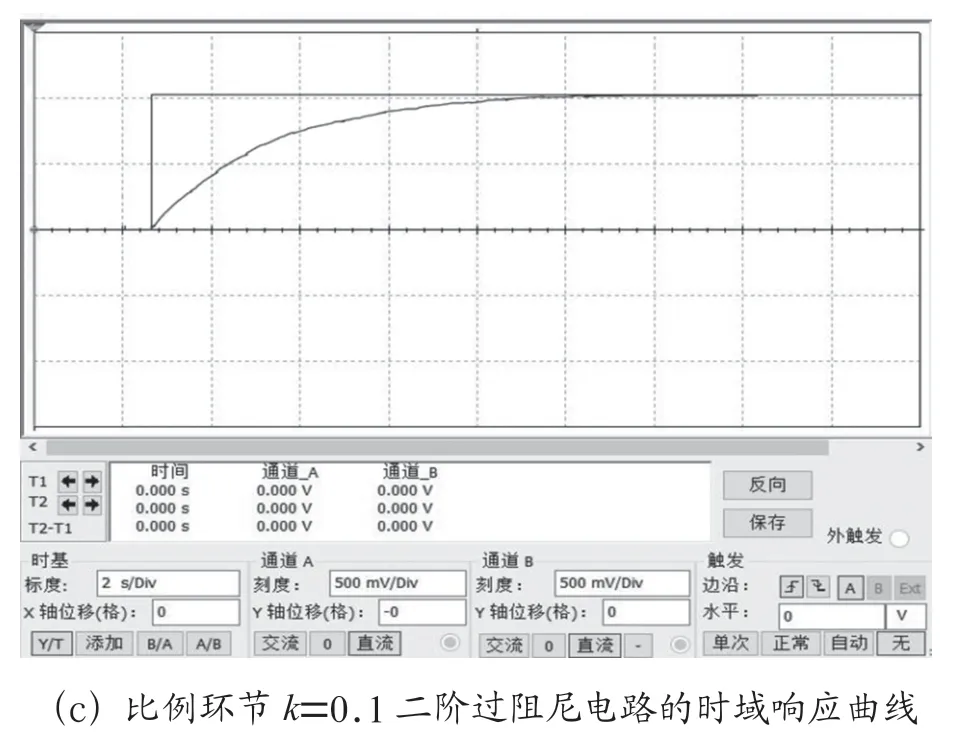
图3 二阶无阻尼及过阻尼电路的时域响应曲线
比例环节中支路s2或s3接通时二阶电路都处于欠阻尼状态,其时域响应曲线如图4所示。图2中,开关s1、s2、s6接通,比例环节=6.25,得到如图4(a) (b)所示的二阶欠阻尼电路单位阶跃响应曲线;开关s1、s3、s6接通,比例环节=12.5,得到如图4(c)(d)所示的二阶欠阻尼电路单位阶跃响应曲线。
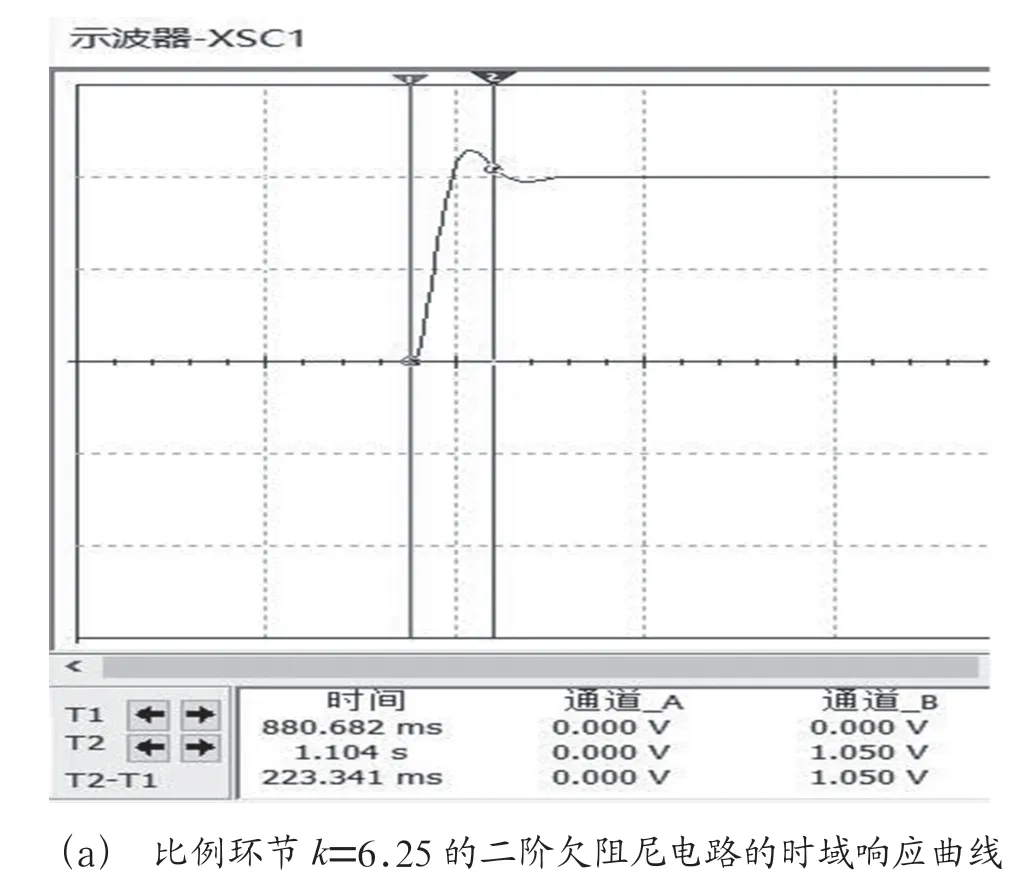
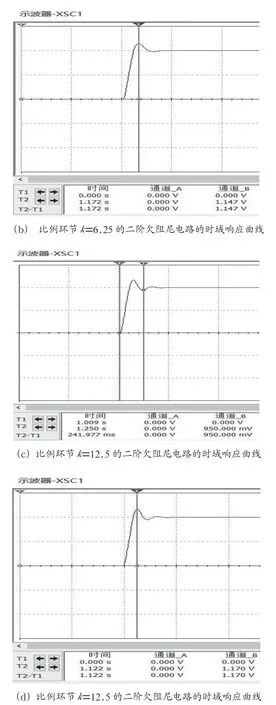
图4 二阶欠阻尼电路的时域响应曲线
图4中,二阶欠阻尼电路的稳态值等于输入电压1 V,游标T1在起始端与游标T2在稳定值正负5%处的时间差即电路的调节时间。比例环节=6.25的二阶欠阻尼电路的时域响应曲线中,图4(a)有一个波峰和波谷,调节时间223.3 ms,图4(b)波峰1.147 V。比例环节=12.5的二阶欠阻尼电路的时域响应曲线中,图4(c)有两个波峰和一个波谷,调节时间240.0 ms,图4(d)首个波峰1.17 V。可见,二阶欠阻尼电路增益越大,则阻尼比越小,电路振荡越厉害。
3.2 二阶欠阻尼系统的MATLAB程序仿真二阶过阻尼系统调节时间较长较少应用,下面对二阶欠阻尼系统利用公式(1)进行MATLAB编程。比例环节=6.25的二阶欠阻尼系统编写如下MATLAB程序。
num=625;den=[1 25 625];
t=0:0.01:2;
y=step(num,den,t); %求单位阶跃响应
ym=max(y) %求振幅
ys=y(length(t)) %求稳态响应值
disp([sgm=,num2str(100*(ym-ys)/ys),%]) %求最大超调量
for i=1:201
if y(i)==ym n=i;end %求振幅对应的点
end
i=201;while i>0 i=i-1;%倒求进入误差带的下标
if y(i)>= 1.05*ys; y(i)<y(i-1); m=i; break;
end%求误差上限进入误差带的下标
if y(i)<= 0.95*ys; y(i)>y(i-1); m=i;break;
end%求误差下限进入误差带的下标
end
ts=m*0.01 %求调节时间
运行MATLAB得到如图4(a)所示的二阶欠阻尼系统单位阶跃响应曲线:振幅y=1.161 9 v,稳态值y =1.000 0 V,最大超调量sgm=16.186 2%,调节时间t=0.22 s。与前面的multisim仿真比较,结果接近。
比例环节=12.5的二阶欠阻尼系统更改num、den参数得到如图5(b)所示的二阶欠阻尼系统单位阶跃响应曲线:振幅y=1.300 4 v,稳态值y=1.000 0v,最大超调量sgm=30.043 6%,调节时间t= 0.23s。与前面的multisim仿真比较,振幅略有误差,结果也是接近的。
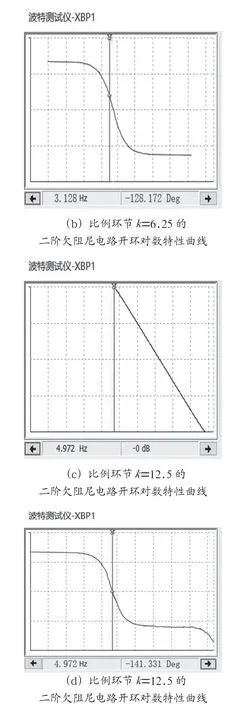
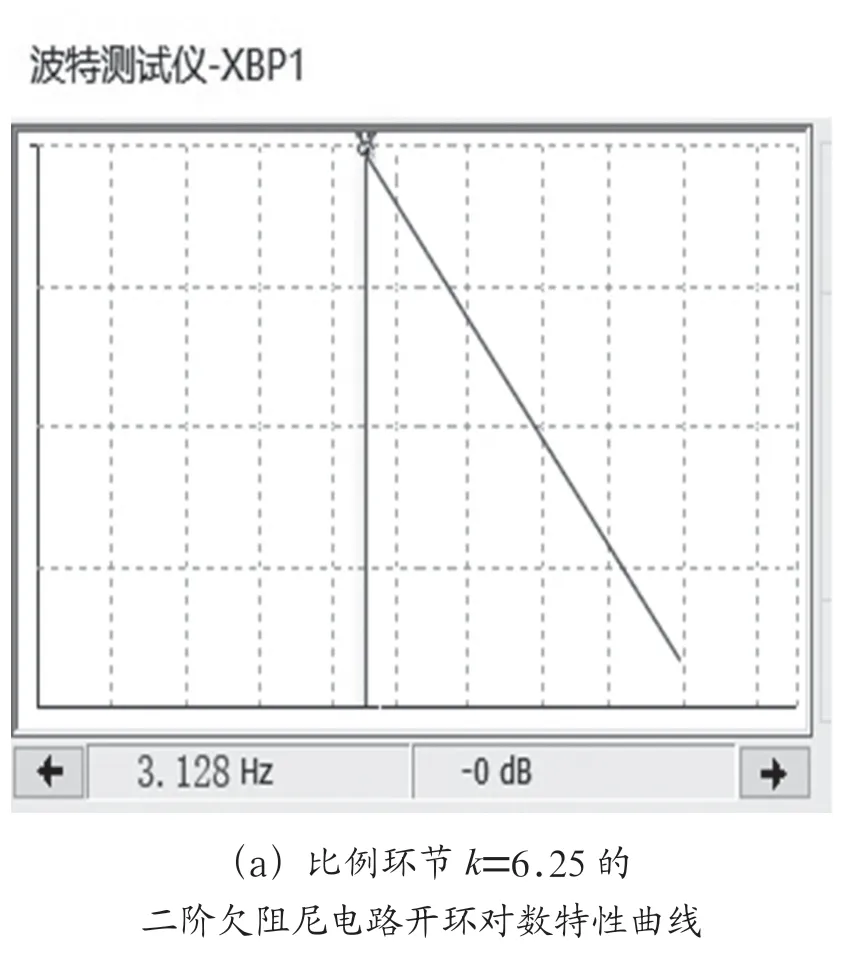
图5 二阶欠阻尼电路开环对数特性曲线
4 二阶欠阻尼电路及系统的频域仿真4.1 二阶欠阻尼电路的Multisim频域仿真图2中交流电源替代直流电源,去掉反馈线,用波特表代替示波器观察开环电路得到二阶欠阻尼电路开环对数特性曲线图5所示。在图5(a)所示的对数幅频特性曲线上,比例环节=6.25幅值穿越频率为3.128 Hz。在图5(c) 所示的对数幅频特性曲线上,比例环节=12.5的幅值穿越频率为4.972 Hz。在图5(b)的比例环节=6.25的对数相频特性曲线上,对应于幅值穿越频率3.128 Hz的穿越相位分别为-128.2°(相位裕度51.8°)。在图5(d)的比例环节=12.5的对数相频特性曲线上,对应于幅值穿越频率4.972 Hz的穿越相位分别为-128.2°(相位裕度51.8°)。
4.2 二阶欠阻尼系统的MATLAB频域仿真去掉反馈环节,如图1所示的二阶系统的开环传递函数为:
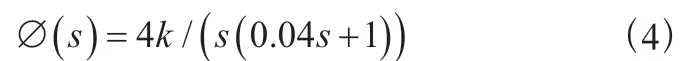
对于比例环节=6.25的二阶欠阻尼系统,根据公式(4)可编写如下MATLAB程序。
num=25; den=conv([0.04 1],[1 0]);
w=logspace(-1,4);
[mag,pha,w]=bode(num,den,w);
[gm,pm,wcg,wcp]=margin(mag,pha,w)
运行可得:相位裕度p=51.836 6,幅值穿越频率w=19.633 4/6.28 Hz=3.12 Hz。这与上述multisim频域仿真吻合得也很好。
更改num、den参数可得:相位裕度p=38.766 9,幅值穿越频率w=31.1781/6.28 Hz=4.96 Hz。这也与上述multisim频域仿真吻合得也很好。
5 结 论本文通过二阶运放电路实现二阶系统,并用Multisim进行时域和频域仿真,同时用MATLAB数值运算对二阶系统进行时域和频域分析,用Multisim电路进行仿真,比MATLAB的数值运算更简便、准确,大大减小了工作量。
Multisim仿真过程真实地反映了自动控制系统的电路工作过程,它打通了电路模型与控制理论的联系。用Multisim仿真去设计和分析控制系统,分析过程相当简便,可见Multisim仿真的分析方法确实值得我们学习和掌握。

