

收稿日期:2023-08-04
基金项目:南京医科大学康达学院科研发展项目(KD2023KYJJ025)
DOI:10.19850/j.cnki.2096-4706.2024.05.032
摘" 要:针对药房批量取药这一现实问题,在设计药房整体环境布局和引入路径规划算法的基础上,提出以重量加权的距离为目标的旅行商问题TSP(Traveling Salesman Problem)。建立一个混合整数规划模型,使用禁忌搜索算法进行模型求解,使用曼哈顿距离作为两点之间距离,在禁忌长度等参数设置上使用动态自适应方法,并在算法中加入扰动方法,避免算法陷入局部最优,增加搜索目标的多样性。最后使用JAVA进行了仿真模拟实验,可视化结果验证了算法的可行性和有效性。
关键词:医药物流;路径规划;药房批量取药;旅行商问题;禁忌搜索算法
中图分类号:TP18;R95" " 文献标识码:A" 文章编号:2096-4706(2024)05-0149-06
Research on Path Planning in Pharmacy Batch Picking Medicine Based on
Improved Tabu Search Algorithm
QIU Yuan, GONG Xingyu
(Kangda College of Nanjing Medical University, Lianyungang" 222000, China)
Abstract: Based on the design of the overall environment layout of pharmacies and the introduction of path planning algorithms, a Traveling Salesman Problem (TSP) with weight weighted distance as the objective is proposed to address the practical problem of pharmacy batch picking medicine. It establishes a mixed integer programming model, uses tabu search algorithm for model solving, uses Manhattan distance as the distance between two points, uses dynamic adaptive methods in setting parameters such as tabu length, and adds a shake method to the algorithm to avoid getting stuck in local optima and increase the diversity of search targets. Finally, simulation experiments are conducted using JAVA, and the visualization results have verified the feasibility and effectiveness of the algorithm.
Keywords: pharmaceutical logistics; path planning; pharmacy batch picking medicine; TSP; tabu search algorithm
0" 引" 言
目前国内药房的药品存储方式主要为固定式货架,平时药房大量简单重复的取药工作耗费了很多不必要的人力物力,且在效率和准确率方面也有待提高[1,2]。在此背景下,本文将路径规划算法应用到药房取药问题中,在国内大部分药房为固定式货架的基础上进行取药路径规划的研究,首先搭建药房环境模型并描述取药过程,将药房批量取药问题转换为一个考虑药品重量的TSP问题,使用曼哈顿距离作为两点之间距离,建立一个混合整数规划模型,然后使用禁忌搜索算法规划最优路线,基于传统的禁忌搜索算法在参数自适应设置和增加扰动方法上进行改进,最后使用JAVA进行仿真模拟实验,设计三类实验算例包括直线取药、同侧异路取药以及异侧异路取药,展示可视化结果并讨论路径规划效果。将路径规划运用到药房取药工作中去,既能提高药师的工作效率,减轻药房管理工作的负担,也能减少患者取药的等待时间,提高患者的就诊体验,对医疗机构整体质量的提升具有实际意义;另外也希望本文的研究结果能够为机器人自动取药的研究[3-8]奠定一定基础。
1" 药房批量取药问题描述与模型建立
1.1" 药房环境建模
本文以药房批量取药为研究对象,首先需要对药房环境进行建模。现如今普遍的药房布局分为垂直式布局、倾斜式布局以及区别于前两者的非传统布局[9],垂直式布局可细分为横列式、纵列式以及纵横式,特点是主副通道纵横交错,整体布局整齐美观,便于存取盘点;而倾斜式布局能够把存储空间划分为具有不同特点的区域,大致分为货架倾斜式和通道倾斜式;非传统布局的典型代表为V式货架,可以区分需大量储存和少量储存的不同部分以便综合利用,但这种布局形式复杂,路径较多不好计算[10]。本文基于国内大部分药房药品存储的固定式货架,并借鉴Kiva系统仓库模型[11],假定药房大小和药架位置固定不变,药架采用单侧开式格子类,一个格子仅存放一种药品,两个单侧药柜背靠式排放,药房通道采用传统的纵横式通道布局方法,由作为主通道的横向通道和作为副通道的纵向通道组成的十字交叉通道,存放药品的药柜与主通道相垂直,设定副通道可作为多种药品的取药点。
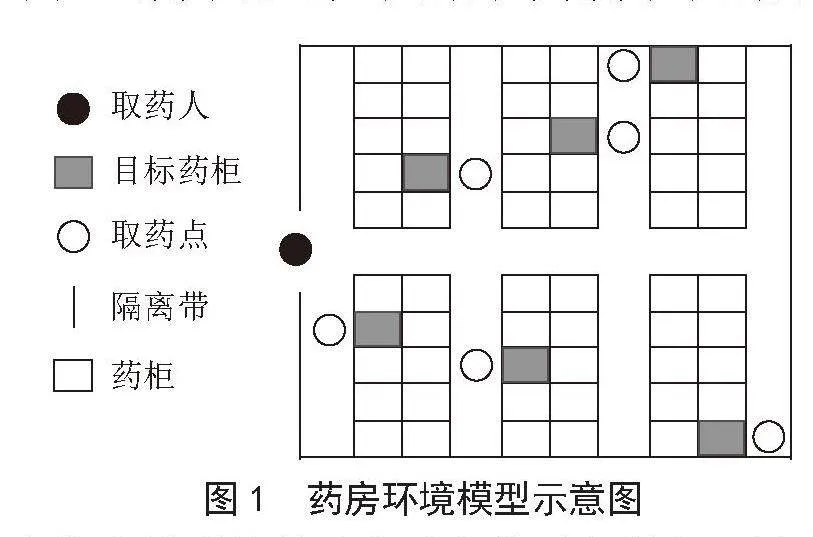
药房环境模型如图1所示。药房环境模型由药柜、取药人、取药点、通道及隔离带组成,其中黑点表示取药人,图1中黑点所在位置为取药过程的起点和终点,矩形表示药柜,药柜中标灰的部分代表目标药柜即所取药品的所在位置,白点代表取药点,实线表示隔离带,一般为墙壁不可通行,其余为可通行区域。
图1" 药房环境模型示意图
在药房模型的基础上对取药过程做如下设定:
1)取药过程中固定起点与终点,且起点和终点是同一个,一次完整的取药过程需要从起点出发并最终返回起点。
2)取药方式默认单侧仅可取该侧药品且只能在目标药柜正对面的取药点取药。
3)取药时在药房通道内只能进行直角转向。
4)每次取药可取多种药品,且每种药品数量确定,即在一次取药过程中取完所有种类药品的对应数量后再返回起点。
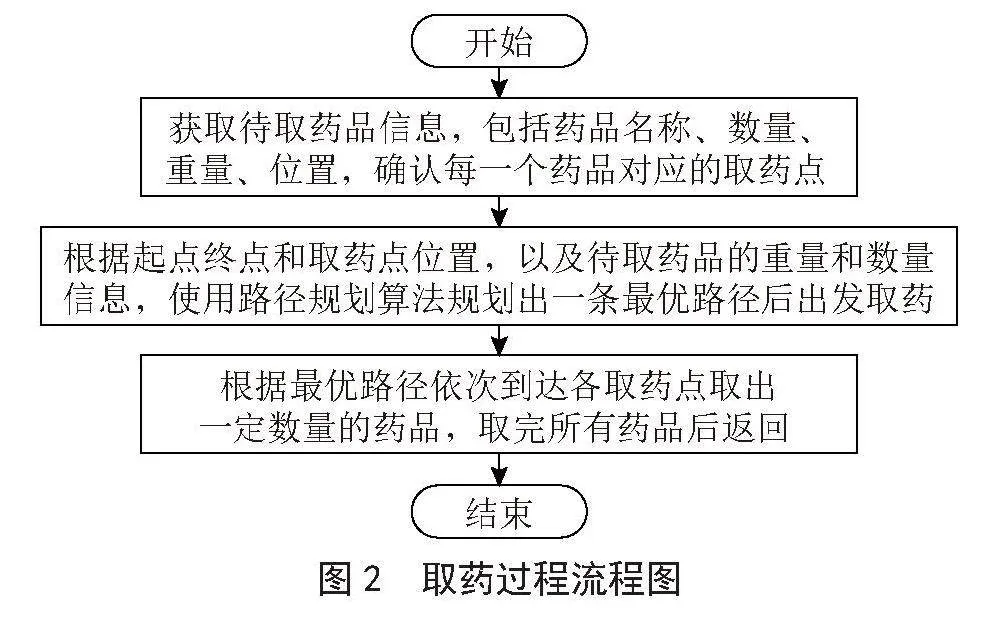
在本文建立的药房模型中,取药过程大致如图2所示。模型建立在二维坐标系上,取药人每次取药需要从起点出发经过所有目标药柜对应的取药点进行取药操作后再回到起点,思考如何规划考虑药品重量的取药最优路线。因此,可以将药房批量取药问题转换为起点终点固定、以重量加权的距离为目标的TSP问题。
1.2" 混合整数规划模型
数学模型定义在一个有向图G = (V,E),其中V = {0,1,2,…,n}是节点集合,包括起点{0}、终点{n}和取药点集合A,E表示两两节点间可能的有向边的集合。现要为每次取药过程规划出一条取药路径,目标是使重量加权距离之和最小。
图2" 取药过程流程图
1.2.1" 模型参数
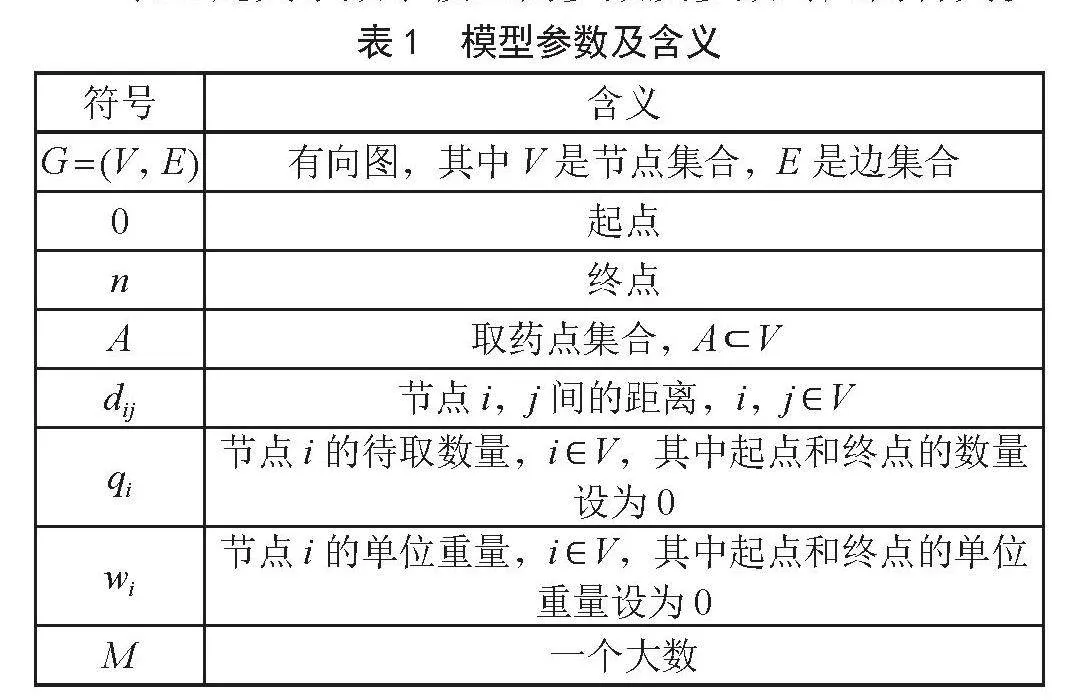
表1定义了数学模型的参数及参数对应的含义。
表1" 模型参数及含义
符号 含义
G = (V,E) 有向图,其中V是节点集合,E是边集合
0 起点
n 终点
A 取药点集合,A ⊂ V
dij 节点i,j间的距离,i,j ∈ V
qi 节点i的待取数量,i ∈ V,其中起点和终点的数量设为0
wi 节点i的单位重量,i ∈ V,其中起点和终点的单位重量设为0
M 一个大数
1.2.2" 模型决策变量
数学模型的决策变量有Xij、Yi,各变量对应的含义如表2所示。
表2" 模型决策变量及含义
决策变量 含义
Xij 0,1变量,1表示经过边(i,j),否则为0
Yi 到达节点i时已取药品的总重量(不包括节点i处的药品重量)
1.2.3" 数学模型
建立如式(1)至式(7)所示的混合整数规划模型:
min" " " " " " " " " " " "(1)
s.t." " " "(2)
(3)
(4)
(5)
(6)
(7)
式(1)为目标函数,表示最小化重量加权距离之和。式(2)至式(7)为约束条件,式(2)至式(4)为流平衡约束,式(2)表示如果到达某个取药点,取完药品后必须离开该点,式(3)(4)确保每个目标取药点均被访问且仅被访问一次;式(5)表示在两个连续节点的载重关系,即在到达取药点时已取药品的总重量等于到达上一个取药点时已取药品的总重量加上该取药点的待取药品重量;式(6)(7)为决策变量的定义域,Xij为0,1变量,Yi大于等于0。
2" 改进禁忌搜索算法的设计
2.1" 算法框架
禁忌搜索算法由美国科罗拉多大学教授Glover[12]提出,是一种全局搜索寻优算法,具有全局逐步寻优的能力,是局部搜索算法的优化与发展[13]。本文使用一种改进的禁忌搜索算法求解模型,基于传统的禁忌搜索算法,使用曼哈顿距离作为两点之间距离,在禁忌长度等参数设置上使用动态自适应方法,并在算法中加入扰动方法,避免算法陷入局部收敛,增加搜索多样性。
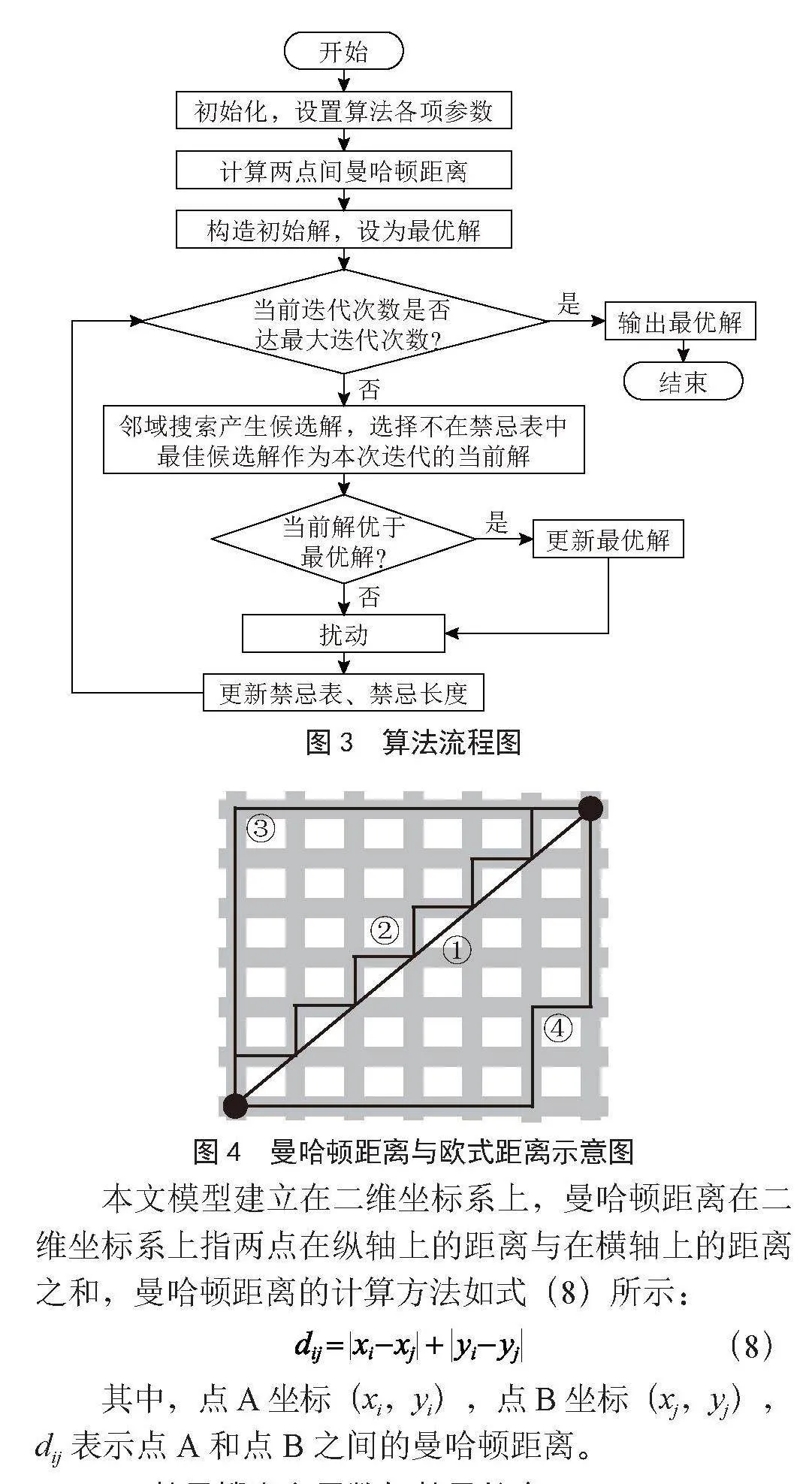
图3为改进禁忌搜索算法的算法流程图,算法的大致步骤为:
1)初始化算法的各项参数,包括禁忌表、禁忌长度、迭代次数等,计算曼哈顿距离作为两点之间距离,随机生成一个初始可行解,从初始解出发进行邻域搜索。
2)以当前解为一次迭代的起点进行邻域搜索,每次邻域搜索产生许多候选解,将不在禁忌表中的最优候选解记为本次邻域最优解。
3)将本次邻域最优解与全局最优解进行比较,若优于全局最优解则将全局最优解替换。然后进行扰动操作,随机选择邻域解以跳出局部最优,同时更新禁忌表和禁忌长度,即如果禁忌表中存放的解的禁忌次数达到禁忌长度,那么将这些解从禁忌表中解禁退出。
4)若达到算法终止条件,即迭代次数达最大迭代次数,则算法停止,输出最优解,否则回到Step2继续进行新一轮的邻域搜索。
2.2" 算法核心模块设计
2.2.1" 计算两点之间的距离——曼哈顿距离
曼哈顿距离(Manhattan Distance)是19世纪赫尔曼·闵可夫斯基所创词汇,大部分使用在几何度量空间中,表明两个点在标准坐标系上的绝对轴距总和[14]。曼哈顿距离可以被理解为投影后的距离,如图4所示,线①为欧氏距离即直线距离,线②为曼哈顿距离,线③和④代表等价的曼哈顿距离,这四条线虽然长短不一但理论上它们长度是等价的。毫无疑问两点之间直线距离最短,但在实际情况中往往两点之间会存在许多障碍物导致直线路线不可通行,此时则可以使用等价的曼哈顿距离。
图3" 算法流程图
图4" 曼哈顿距离与欧式距离示意图
本文模型建立在二维坐标系上,曼哈顿距离在二维坐标系上指两点在纵轴上的距离与在横轴上的距离之和,曼哈顿距离的计算方法如式(8)所示:
(8)
其中,点A坐标(xi,yi),点B坐标(xj,yj),dij表示点A和点B之间的曼哈顿距离。
2.2.2" 禁忌搜索主函数与禁忌长度
禁忌搜索中的主函数也称为评价函数,是用来评价邻域解优劣的衡量指标。本文研究的药房批量取药问题考虑药品重量,建立以重量加权距离之和为目标函数的数学模型,因此本算法采用重量加权距离进行评价,即重量加权距离之和越小则表示解越优。
禁忌表的两项主要指标分别为禁忌对象和禁忌长度,本算法以节点i为禁忌对象建立一维禁忌表;使用动态自适应方法设置禁忌长度,对每个节点i设置参数Fi来记录节点i在邻域搜索中被访问的次数,禁忌长度的具体计算方法如式(9)所示:
(9)
其中Ti表示节点i的禁忌长度,iter表示当前迭代次数,λ表示调整参数,需根据不同算例进行调整设置。该动态自适应的方法能够确保在邻域搜索过程中被频繁访问的节点的禁忌长度更大,防止出现由于禁忌长度过长导致计算量过大运算时间慢以及禁忌长度过短导致陷入局部收敛的问题。
2.2.3" 扰动方法
在算法中加入扰动方法,即一些随机移动和随机搜索,可以避免算法陷入局部最优以及陷入局部最优后能够快速跳出,同时也能增加搜索的多样性。扰动方法需设置扰动长度和扰动次数两个参数,在禁忌搜索的迭代过程中,当最优解未被更新的次数等于扰动长度时,触发算法进入扰动步骤,开始进行一定次数即扰动次数的随机搜索。
3" 仿真实验及可视化结果
3.1" 实验算例
基于图1搭建的药房模型并考虑实际取药场景,设计三类实验算例对模型和算法进行仿真实验,展示可视化结果并讨论路径规划效果,三类实验场景分别为:
1)直线取药,所有取药点位于同一直线副通道上。
2)同侧异路取药,取药点位于主干道一侧且跨越多条副通道。
3)异侧异路取药,取药点跨越主干道两侧且同时跨越多条副通道。
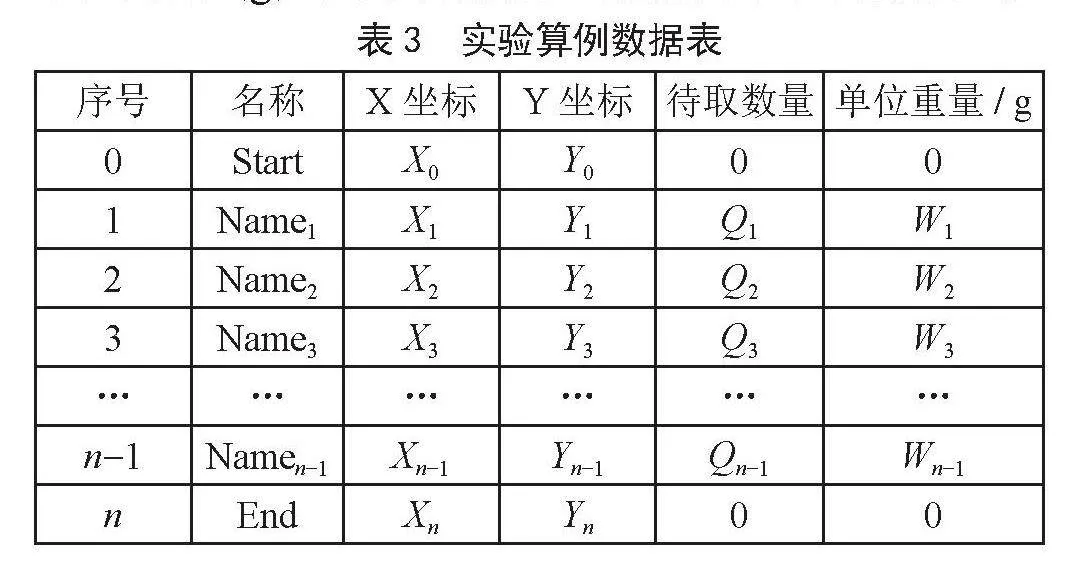
表3为实验算例数据表,提供算例包含的数据信息。“序号”表示起点终点和取药点的编号,其中序号0为起点,序号n为终点,序号1到n-1代表有n-1个取药点,算法实现的结果使用节点序号组成的一条路径来表示,举例说明,若算法得出的最佳路径表示为“0-gt;1-gt;n-1-gt;…-gt;2-gt;n”,则该条取药线路为从起点0(X0,Y0)出发,先到达取药点1(X1,Y1)拣取对应目标药柜的药品,接着去取药点n-1(Xn-1,Yn-1)取药,然后依次按照最佳路径的序号次序到达对应取药点,最后到达取药点2(X2,Y2),取完取药点2对应目标药柜的药品后,最终回到终点n(Xn,Yn);“名称”为药品名称,其中起点和终点的名称设定为Start和End;“X坐标”和“Y坐标”表示起点终点和取药点的位置信息,分别为坐标轴中各点的X、Y坐标,并根据X、Y坐标数据计算曼哈顿距离作为节点间的距离;“待取数量”表示药品需要拣取的数量,其中起点和终点的数量设为0;“单位重量”表示单个药品的重量,比如每盒重量、每瓶重量等,单位为克(g),其中起点和终点的单位重量设为0。
表3" 实验算例数据表
序号 名称 X坐标 Y坐标 待取数量 单位重量/ g
0 Start X0 Y0 0 0
1 Name1 X1 Y1 Q1 W1
2 Name2 X2 Y2 Q2 W2
3 Name3 X3 Y3 Q3 W3
… … … … … …
n-1 Namen-1 Xn-1 Yn-1 Qn-1 Wn-1
n End Xn Yn 0 0
3.2" 可视化结果展示及分析
仿真实验使用JAVA语言实现,基于Windows 10操作系统、IntelliJ IDEA开发平台,使用JavaFX实现可视化效果。对3.1中设计的三类实验场景分别构造多组不同规模的算例,进行仿真实验并分析实验结果,通过可视化展示取药路径轨迹来验证算法的有效性和可行性。本文分别对每类场景选取一组算例详细分析其实验结果。
3.2.1" 直线取药
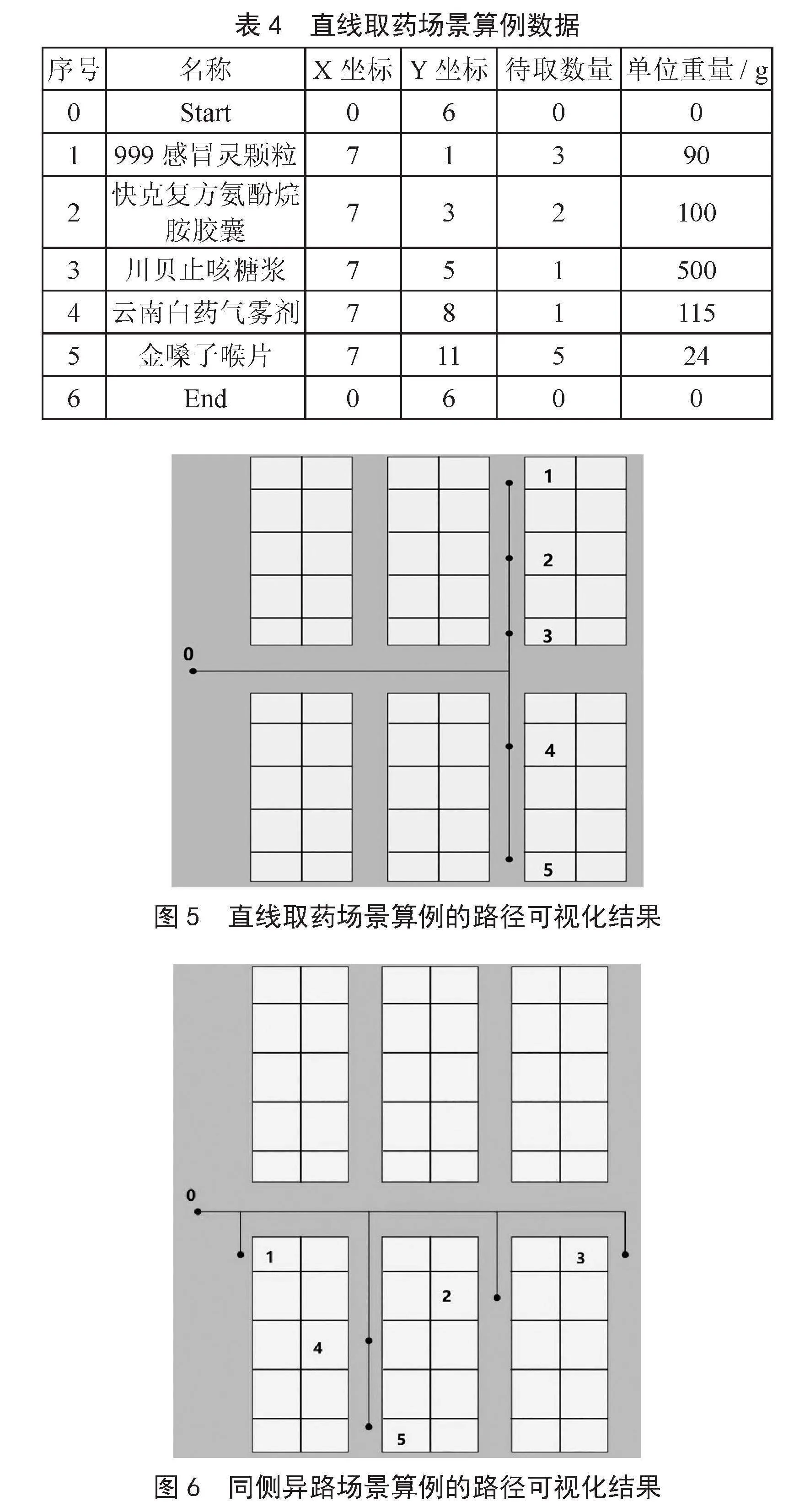
直线取药场景指所有取药点位于同一直线副通道上。表4给出直线取药场景其中一组算例的具体数据,该算例设置了5个取药点,取药点的位置如图5所示,5个取药点均在第三条副通道上且分布在主干道两侧,其中取药点1、取药点2、取药点3位于主干道左侧即图5中显示的主干道上方,取药点4和取药点5位于主干道右侧即图5中显示的主干道下方。图5为该算例的路径可视化结果,算法求得的最佳路径为0→5→4→1→2→3→6,可以看出该解准确且可行。观察和分析图5中最优路径轨迹可以发现,规划出的最佳路径优先到达取药点4和取药点5所在的主干道右侧药架,而且在同一药架的取药顺序以离主干道更远的取药点优先,比如主干道左侧药架的取药顺序为1→2→3而主干道右侧药架的取药顺序为5→4,这是因为药房批量取药问题考虑了药品的重量加权距离,而主干道右侧药架待取药品的总重量大于左侧药架待取药品的总重量,且先拣取远端的药品都能使得总的重量加权距离这一目标函数更小。
3.2.2" 同侧异路取药
同侧异路取药场景指取药点位于主干道一侧且跨越多条副通道。图6路径可视化结果中显示了该算例起点终点和取药点的位置分布,5个取药点均在主干道右侧且分布在四条不同的副通道上,其中取药点1在第一条副通道上、取药点2在第三条副通道上、取药点3在第四条副通道上,取药点4和取药点5在第二条副通道上。算法求得的最佳路径为0→3→2→5→4→1→6,同样能够发现规划后的取药路径是按照不同副通道之间由远至近、同一副通道之上先远后近的顺序。
表4" 直线取药场景算例数据
序号 名称 X坐标 Y坐标 待取数量 单位重量/ g
0 Start 0 6 0 0
1 999感冒灵颗粒 7 1 3 90
2 快克复方氨酚烷胺胶囊 7 3 2 100
3 川贝止咳糖浆 7 5 1 500
4 云南白药气雾剂 7 8 1 115
5 金嗓子喉片 7 11 5 24
6 End 0 6 0 0
图5" 直线取药场景算例的路径可视化结果
图6" 同侧异路场景算例的路径可视化结果
3.2.3" 异侧异路取药
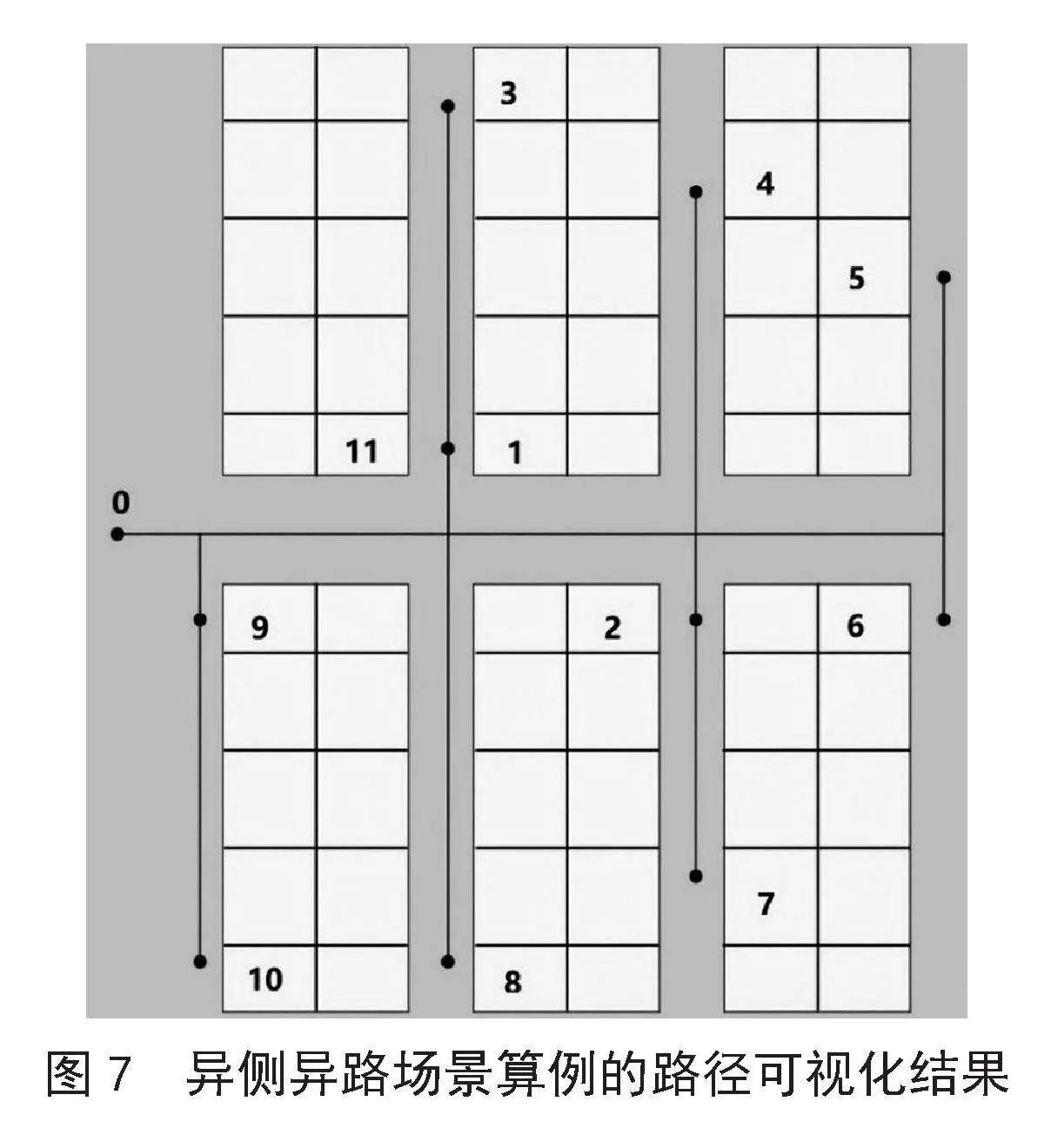
异侧异路取药场景指取药点跨越主干道两侧且同时跨越多条副通道。图7为异侧异路取药场景算例的路径可视化结果,11个取药点的位置分布在主干道两侧和不同的副通道上,其中取药点1和取药点11的位置相同实则为同一取药点,本文设定在同一副通道两侧呈水平的两个药柜可在同一取药点进行取药操作,这种设定符合实际的药房取药场景。算法求得的最佳路径为0→9→10→8→7→2→6→5→4→3→1→11→gt;12,由图7可以明显看出该路径合理且能够按照路径完成取药任务。
图7" 异侧异路场景算例的路径可视化结果
4" 结" 论
本文将路径规划算法运用到药房取药场景上,搭建了一个纵横式布局的药房环境模型,将药房批量取药问题转换为一个考虑药品重量的TSP问题,使用曼哈顿距离作为两点之间距离,建立了一个以重量加权距离之和为目标函数的混合整数规划模型,设计了一种改进的禁忌搜索算法方法求解该模型,最后通过三类实验场景的仿真实验,可视化展示并分析算法在取药路径上有较好的路径规划效果。本方法能够有效地解决药房批量取药问题,可以运用到中小药房和医院药房等医疗机构,但由于实际情况复杂,药房取药场景往往需要考虑更多现实要素,比如药品体积、取药的载重载容约束、以及多趟取药问题等,另外本文的研究结果也为机器人自动取药研究奠定了一定的基础。基于本文后续可进行更深入和完善的研究,进一步提升现实意义。
参考文献:
[1] 刘丽萍,韩晋,谢进,等.解放军302医院门诊药房自动化调剂新模式的实践 [J].药学服务与研究,2007(6):468-469.
[2] 金滔,任丹媛,孙洁,等.医院发热门诊智慧药房的构建与应用 [J].中国药业,2022,31(7):14-17.
[3] 王鹤静,王丽娜.机器人路径规划算法综述 [J].桂林理工大学学报,2023,43(1):137-147.
[4] 陈洋,林其岳,邓志华,等.AGV路径规划算法研究进展 [J].机电技术,2022(5):39-43.
[5] 陈键.无人快递机器人路径规划算法研究综述 [J].价值工程,2022,41(5):166-168.
[6] 林韩熙,向丹,欧阳剑,等.移动机器人路径规划算法的研究综述 [J].计算机工程与应用,2021,57(18):38-48.
[7] 巨雨亭.车间搬运AGV系统设计与路径规划研究 [D].太原:中北大学,2023.
[8] 吉红,赵忠义,王颖丽,等.复杂环境下多AGV路径规划与调度系统研究 [J].机械设计,2023,40(6):110-115.
[9] 熊宇.非传统布局仓储系统AGV调度研究与实现 [D].南昌:南昌大学,2021.
[10] 潘成浩.仓储物流机器人拣选路径规划仿真研究 [D].太原:中北大学,2017.
[11] 陈明智,钱同惠,张仕臻,等.仓储物流机器人集群避障及协同路径规划方法 [J].现代电子技术,2019,42(22):174-177+182.
[12] GLOVER F. Future paths for integer programming and links to articial intelligence [J].Computers amp; Operations Research,1986,13:533-549.
[13] CHANG W B,JI X P,XIAO Y Y,et al. Prediction of Hypertension Outcomes Based on Gain Sequence Forward Tabu Search Feature Selection and XGBoost [J].Diagnostics(Basel,Switzerland),2021,11(5):792-792.
[14] LIU X,LIU X M,ZHANG R L,et al. Securely Computing the Manhattan Distance under the Malicious Model and its Applications [J].Applied Sciences,2022,12(22):11705-11705.
作者简介:邱媛(1995—),女,汉族,江苏连云港人,助教,硕士,研究方向:车辆路径问题、运筹优化算法、医药物流;龚星雨(2001—),女,汉族,上海崇明人,学士,研究方向:路径规划、医学信息工程。

