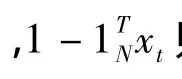



摘" 要:随着云存储和云计算的发展,大量数据被上传及存储在服务器端。针对传统霍夫曼编码设计存在码字长度分布不均匀、码方差偏大、“字符—概率—码字”唯一对应难,引起储存空间占用大、解码误码率高的问题,文章基于“极小量扰动”思想提出一种最小方差霍夫曼编码设计方法。仿真结果表明,该文设计的最小方差霍夫曼编码码字长度分布更均匀,码方差更小,且所得编码能与符号对应;进行文本压缩实验时,压缩率分别为69.6%、65.9%、49.3%,能有效提升编码质量,降低冗余度。
关键词:云存储;霍夫曼编码;最小方差;数据压缩
中图分类号:TN911.21" " 文献标识码:A" 文章编号:2096-4706(2024)09-0087-05
Research on Design and Application of Minimum Variance Huffman Coding
WANG Mengfan1, LI Xiaoyi2, FENG Ketao3, ZHU Gang3, WANG Bin3
(1.School of Computer and Information Science, Chongqing Normal University ,Chongqing" 401331, China;
2.Communication Sergeant School, The Army Engineering University of PLA, Chongqing" 400035, China;
3.Unit 31306 of PLA, Chengdu" 610036, China)
Abstract: With the development of cloud storage and cloud computing, a large amount of data is uploaded and stored on the server side. In response to the problems of uneven codeword length distribution, large code variance, and difficulty in unique correspondence between characters, probabilities, and codewords in traditional Huffman coding design, which lead to large storage space occupation and high decoding error rate, this paper proposes a minimum variance Huffman coding design method based on the concept of “minimal disturbance”. The simulation results show that the minimum variance Huffman coding designed in this paper has a more uniform codeword length distribution, smaller code variance, and the obtained code can correspond to the symbols. When conducting text compression experiments, the compression rates are 69.6%, 65.9%, and 49.3%, respectively, which can effectively improve coding quality and reduce redundancy.
Keywords: cloud storage; Hoffman coding; minimum variance; data compression
0" 引" 言
霍夫曼编码于1952年被David Huffman首次定义[1],它是基于无损压缩的最优前缀码[2],使用概率模型生成编码树[3]。其基本思想是:概率大的信源符号分配短码字,而概率小的信源符号分配长码字。霍夫曼编码是一种可变长度编码技术[4],压缩率通常在20%~90%之间[5],是已经被证明的一种有效紧致码。得益于霍夫曼编码的高效性,其广泛应用于计算机[6]、信息无损压缩[7]、密文可逆信息隐藏[8]、NAND闪存[9]、大容量文本隐写[10]等领域。
随着大数据时代的到来,海量数据的可靠存储成为一个亟待解决的重要问题,引起广泛的关注[11]。文献[12]提出一种基于双霍夫曼的最小方差编码方法,提升了文本信息的无损压缩性能;文献[13]提出一种联合定长编码和霍夫曼编码的密文域可逆信息隐藏算法,借助自然图像相邻像素间的相关性提升了嵌入率;文献[14]提出一种基于改进霍夫曼编码支持大规模动态图的可达查询处理方法,具有良好的可行性和有效性。同时,伴随仿真平台的多元化扩展,文献[15-20]分别使用Python、VC++、Verilog、C语言、MATLAB和FPGA等仿真平台对霍夫曼编码过程进行仿真实现及应用研究。
在云存储技术中,从节约空间资源和提高服务可靠性的角度出发,要求编码码字稳定(码方差越小越好)。然而,以上研究都缺乏对码字长度分布不均匀、码方差偏大、“字符—概率—码字”唯一对应难等问题的深入研究。为此,本文基于MATLAB仿真平台,在“极小量扰动”思想的指引下提出一种最小方差霍夫曼编码设计方法,显著降低了码方差,将其应用于文本信息压缩,有效提升了质量。
1" 传统霍夫曼编码存在不足
传统霍夫曼编码设计在构建霍夫曼树过程对信源进行缩减时,如果两个概率最小的符号合并后的概率与其他信源符号的概率相同,这两者在缩减信源中进行概率排序,其位置可以是任意的[21]。放置次序不同会产生不同的树结构。尽管最终这些树各自编码结果平均码长相等且同为最小,但码方差并不相等。此外,由于对权值相等的根节点排序未做严格区分,在对多个相同概率符号进行编码时容易造成编码结果不唯一,难以实现“字符—概率—码字”的唯一对应,当处理海量大数据时,译码过程更容易产生误码。如将这些码字实时输入到云存储系统,则容易引起系统稳定性下降的问题。
2" 最小方差霍夫曼编码的设计
在不同的编码结果中,只要每一次把根节点权值按升序排列,且将最小两个根节点权值合并后产生的新根节点放置在同权值根节点的最前面(尽可能地减少权值小根节点参与编码的次数,可以减小码长方差),该方式所得编码的码方差最小,可实现最小方差霍夫曼编码。本文基于“极小量扰动”思想的编码设计主要分为构建最小方差霍夫曼树和生成霍夫曼编码两个步骤。
2.1" 构建最小方差霍夫曼树
最小方差霍夫曼编码设计的关键是最小方差霍夫曼树的构建,构建思路如下:
1)N个元素的权值空间,构成含有N棵初始树的森林,设置无穷小量δ,当森林中出现n棵树的权值相同时,设其初始位置分别是i1,i2,…,in,将这n棵树对应加上(N - in) δ / 2N。
2)对森林中各树按权值进行降序排列,选出根节点概率权值最小和次小的两棵树(分别记作左子树、右子树)进行合并。
3)对二者求和后再加上δ建立新树并加入森林,记录两棵子树的位置,然后删除子树。
4)重复2)和3)两个步骤实现森林的更新,直至森林中只剩下一棵树,这棵二叉树即为最小方差霍夫曼二叉树,得到霍夫曼树矩阵。
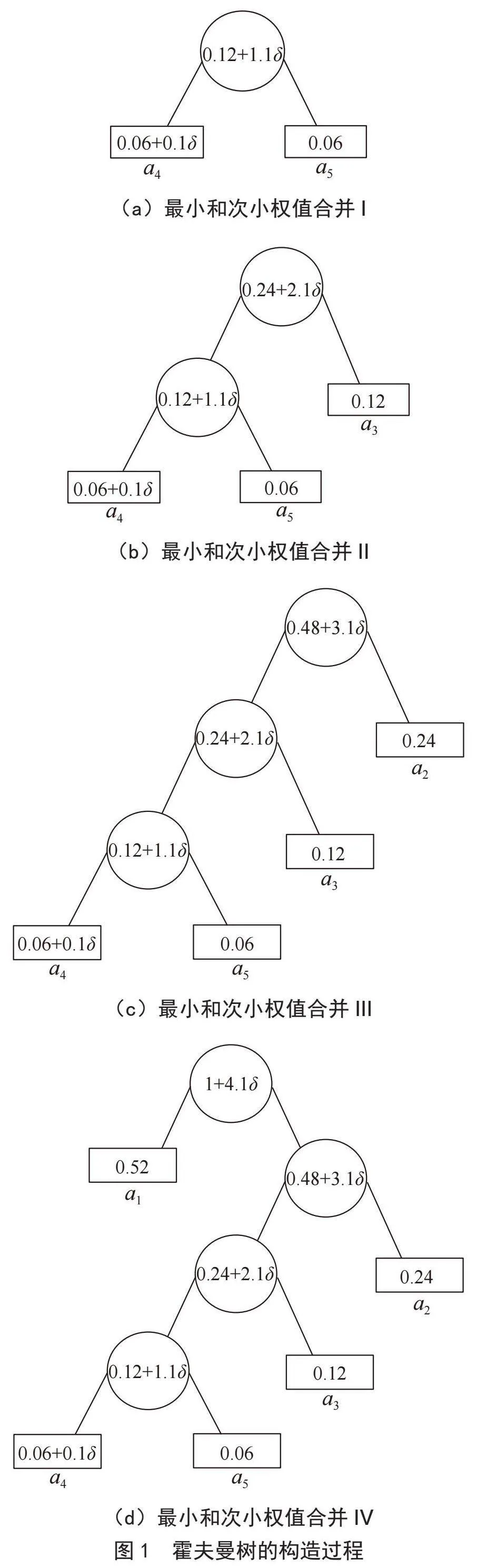
例如,给定的5个字符a1至a5,它们对应的权值集合为W = {0.52,0.24,0.12,0.06,0.06},由于a4 = a5 = 0.06,经过第一步更新后,则有:
构造霍夫曼树的过程如图1所示。
2.2" 生成霍夫曼编码
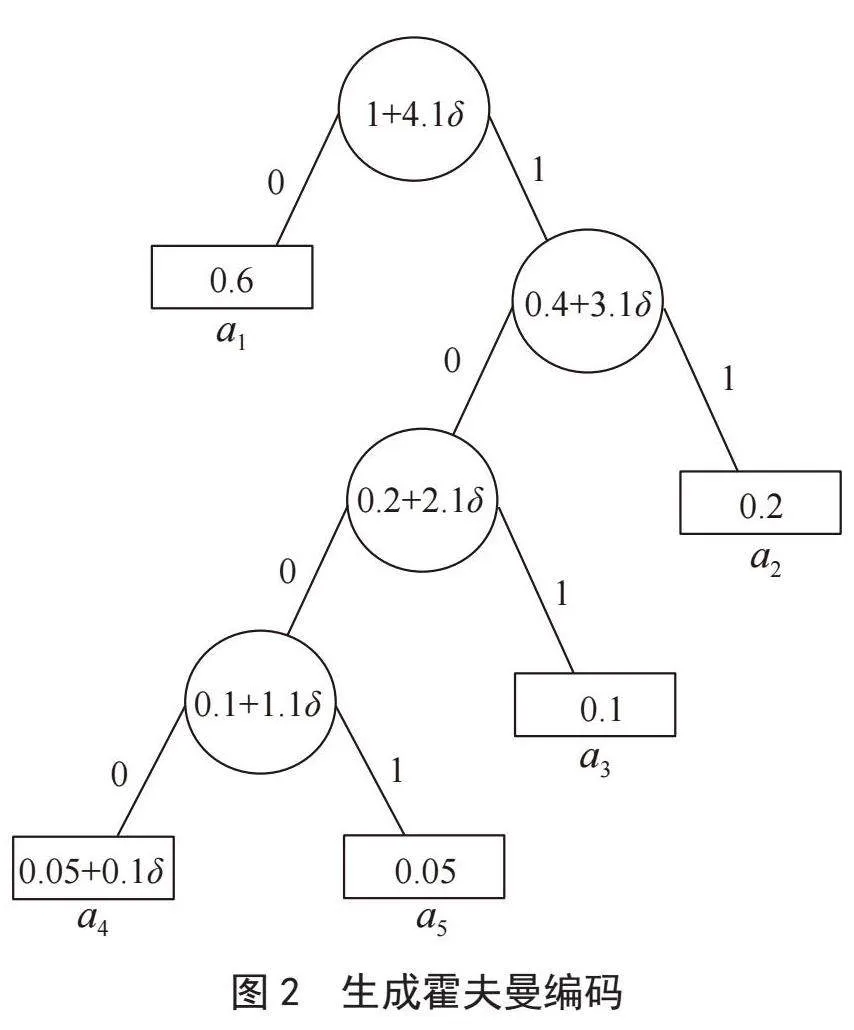
初始森林为最终霍夫曼二叉树的叶子,从每个叶子节点往上找到其父节点,根据霍夫曼树矩阵判断子节点为左子树还是右子树,并编为“1”和“0”存入矩阵。继续向上搜索寻找父节点,直至搜寻到树的根节点,最后将字符矩阵里的字符串按一定顺序输出,得到该叶子(字符)的霍夫曼码。
2.1节示例产生的霍夫曼编码如图2所示。编码结果为a1 = 0,a2 = 11,a3 = 101,a4 = 1000,a5 = 1001。
3" 编码质量评价
为评价霍夫曼编码的质量,使用平均码长、编码效率、码长方差和压缩率等指标进行定量分析。假设字符集合A = {a1,a2,…,aN}共包含N个字符,其对应的概率集合为P = { p1,p2,…,pN},编码码长为L = {l1,l2,…,lN},则A的信源熵为:
平均码长为:
编码效率为:
码长方差为:
码长方差体现的是字符ai的码长li相对于其平均码长的摆动程度,其幅度变化越小,表明其平稳性越好。
压缩率为[22]:
4" 仿真实验与分析
在表示计算机字符时,由于各字符的使用频率存在差异,若采用传统的8位ASCII码表示,存在较大冗余,增加存储空间占用负担。使用霍夫曼编码方法,依据字符频率高低分别用短、长码字表示可有效提升压缩率。
4.1" 实验一
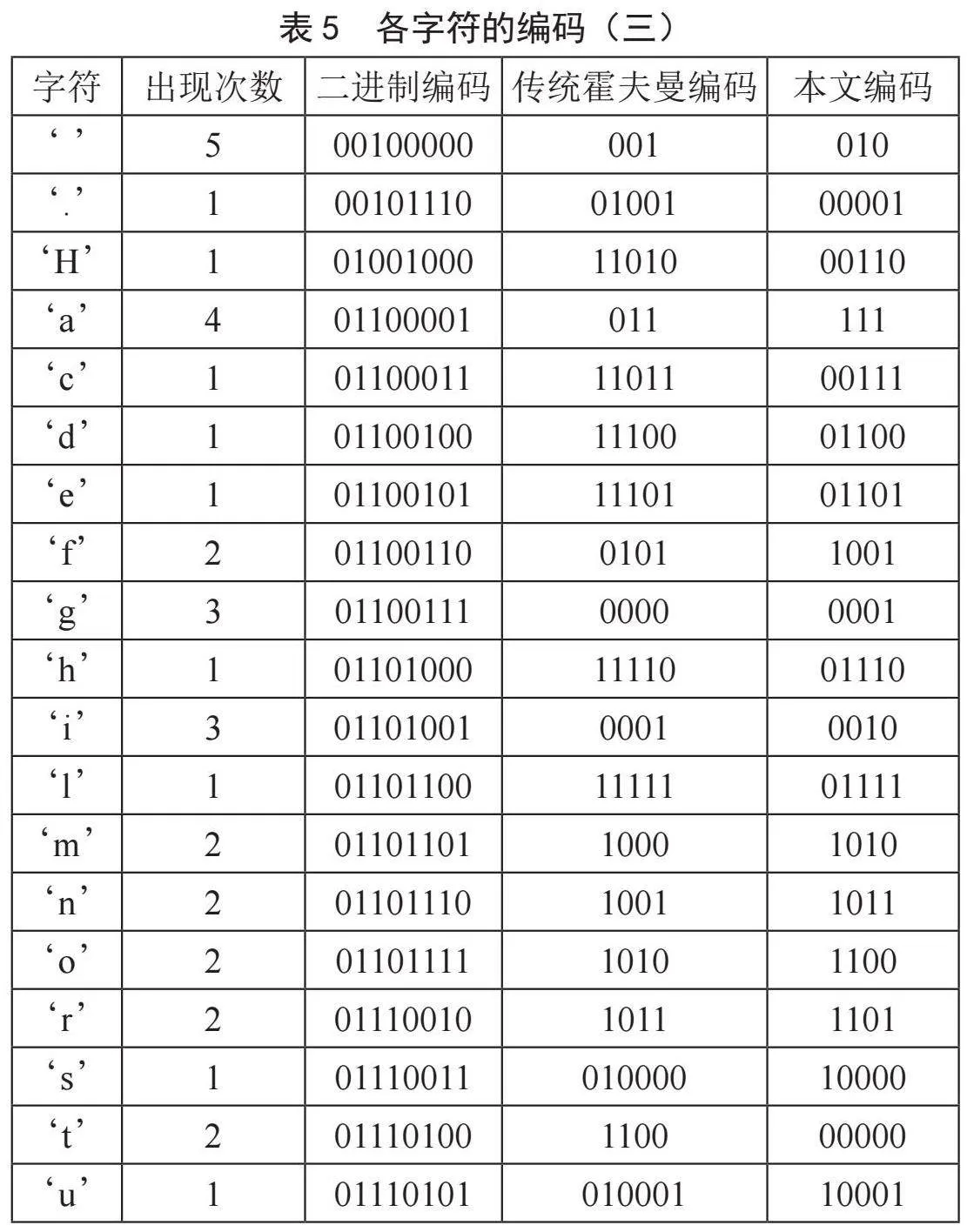
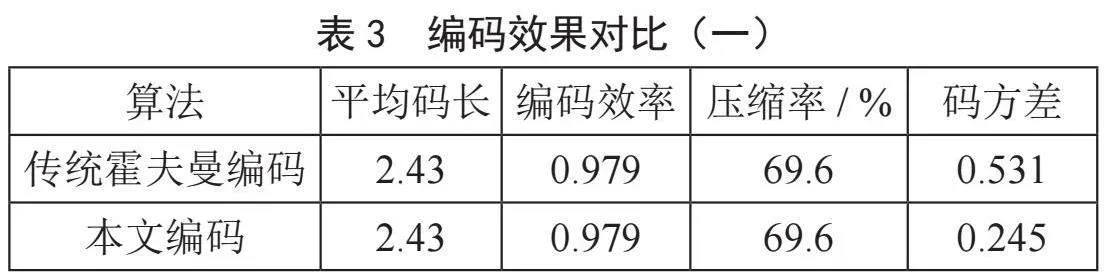
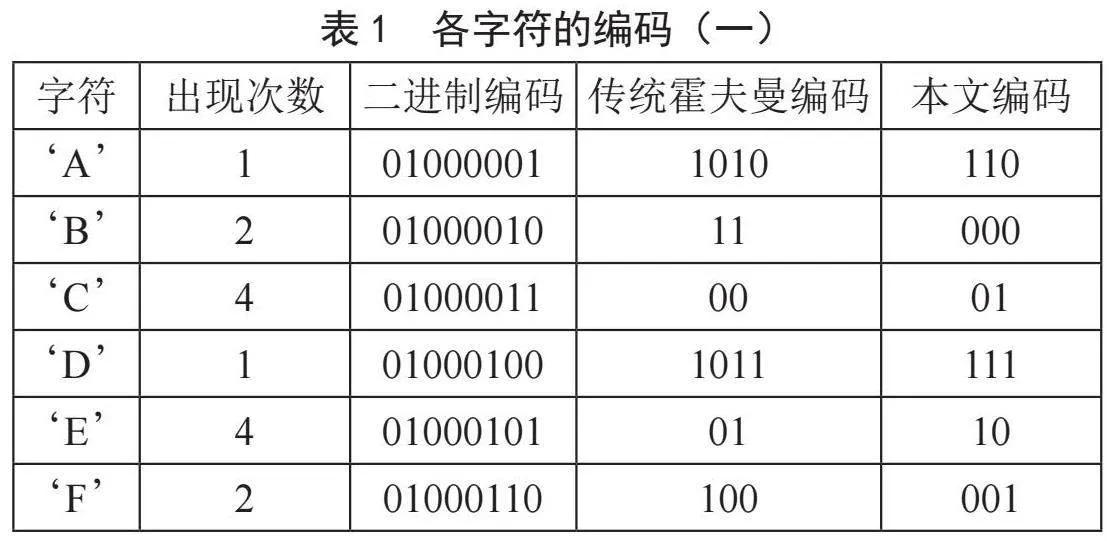
为检验本文编码方法的先进性,设置实验文本分别为“ABBCCCCDEEEEFF”和“ABBbCMMAcAbAcEEEEEEEEN”,对本文编码算法和传统霍夫曼编码算法进行编码质量的对比,得到的编码结果如表1、表2所示。
分析表1至表4可知,与传统霍夫曼编码相比,两种编码设计的编码结果中平均码长、编码效率和压缩率均相同,但本文编码设计的码字长度分布更加均匀,码方差更小。
4.2" 实验二
为直观展示最小方差霍夫曼编码对文本文件压缩的过程,选用一段文本进行编码、解码。实验文本为Huffman coding is a great algorithm.
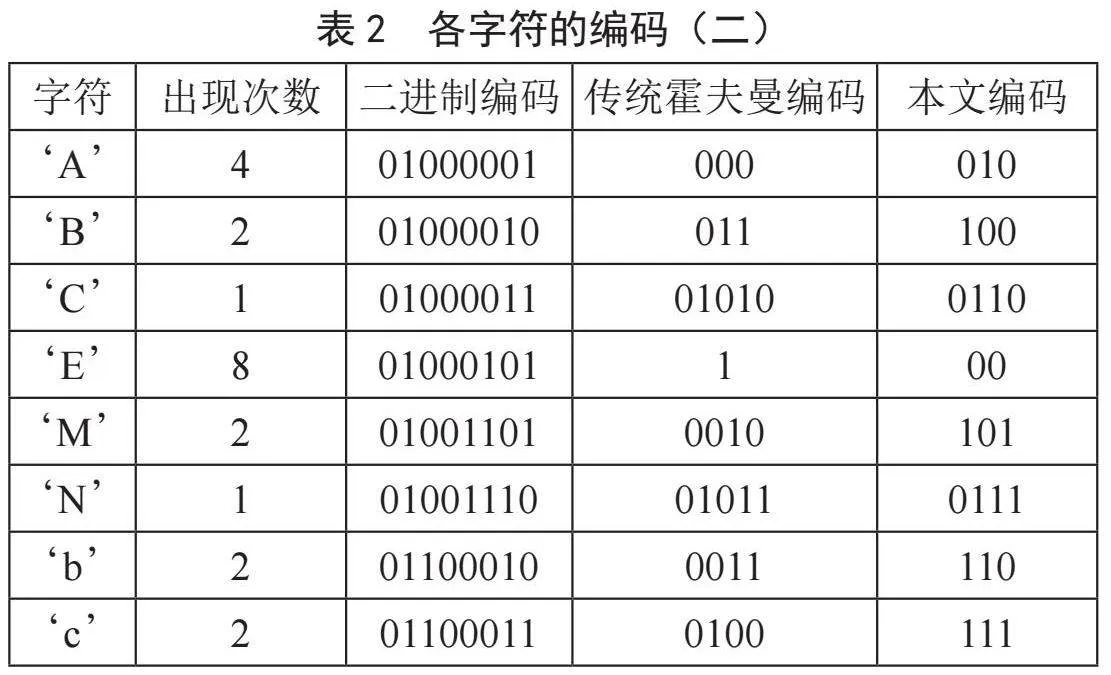
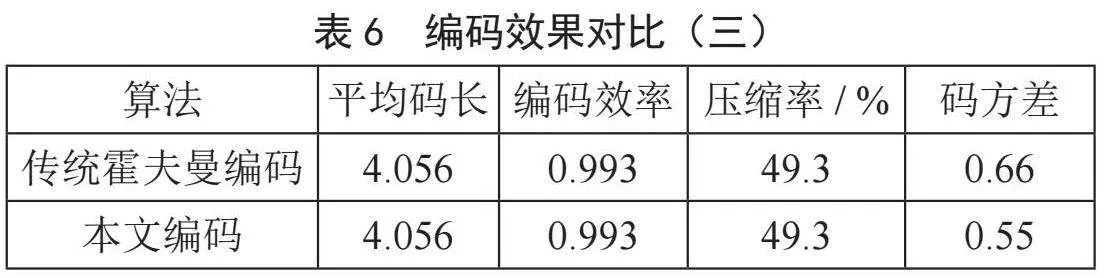
该段文本中含有36个字节,共出现19个不同字符。对各个字符的出现次数进行统计,结果列于表5之中,编码效果对比如表6所示。
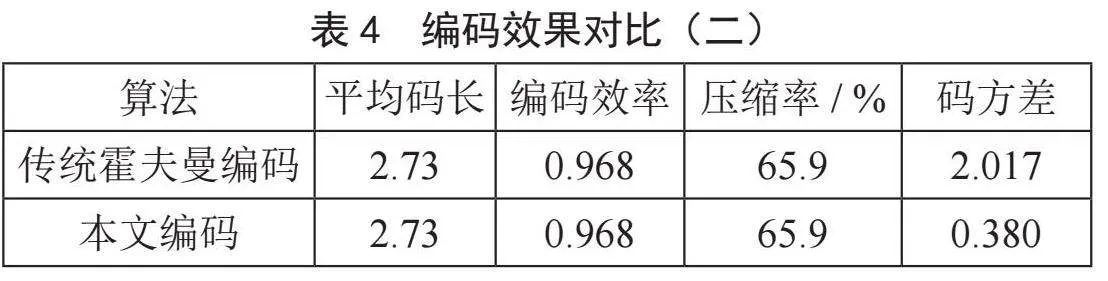
由表6可知,在压缩率对比上,本文编码与传统霍夫曼编码相同,均为49.3%;在码方差对比上,本文编码的码方差为0.55,传统霍夫曼编码的码方差为0.66,显然本文算法更优。
此外,本文的编码设计基于“极小量扰动”思想,在构建霍夫曼树的过程中对权值相等的根节点排序进行区分处理,这样可确保“字符—概率—码字”的唯一对应关系,有效降低系统误码率。
5" 结" 论
本文基于“极小量扰动”思想提出一种最小方差霍夫曼编码设计方案,借助文本压缩实例与传统霍夫曼编码方式进行码字质量对比,本文编码具有最小的码方差,并能有效解决多个相同概率符号与其编码唯一对应难的问题,降低了系统误码率。该编码设计能有效提升编码质量,为最小方差霍夫曼编码设计提供新思路,适用于大数据云存储。
参考文献:
[1] HUFFMAN D A. A Method for the Construction of Minimum-Redundancy Codes [J].Resonance,2006,11(12):91-99.
[2] MALIK A,SIKKA G,VERMA H K. A high Capacity Text Steganography Scheme Based on Huffman Compression and Color Coding [J].Journal of Information and Optimization Sciences,2017,38(5):647-664.
[3] LIANG J Y,CHEN C S,HUANG C H,et al. Lossless Compression of Medical Images Using Hilbert Spac-filling Curves [J].Computerized Medical Imaging and Graphics,2007,32(3):174-182.
[4] 王兆丽,肖春霞,王梅娟,等.哈夫曼编码在图像无损压缩中的应用 [J].计算机工程与科学,2019,41(S1):200-202.
[5] 张雷洪,叶华龙.基于哈夫曼编码的关联成像算法的图像传输机理研究 [J].包装工程,2019,40(5):244-249.
[6] 李宜珂,王旃.基于不同排序方法的快速霍夫曼编码硬件实现 [J].计算机科学,2017,44(S2):476-479+509.
[7] CADAVID J M,MADRIGAL H D V. A Lossless Compression Method for Chat Messages Based on Huffman Coding and Dynamic Programming [J/OL].Computers,2021,10(3)[2023-07-08].https://www.mdpi.com/2073-431X/10/3/28.
[8] 吴友情,郭玉堂,汤进,等.基于自适应哈夫曼编码的密文可逆信息隐藏算法 [J].计算机学报,2021,44(4):846-858.
[9] WU C H,ZHANG H W,LIU C W,et al. A Dynamic Huffman Coding Method for Reliable TLC NAND Flash Memory [J].ACM Transactions on Design Automation of Electronic Systems,2021,26(5):1-25.
[10] MALIK A,SIKKA G,VERMA H K. A high capacity text steganography scheme based on huffman compression and color coding [J].Journal of Information and Optimization Sciences,2017,38(5):647-664.
[11] 王龙江,陈越,严新成,等.网络编码云存储系统差分数据更新方案 [J].通信学报,2017,38(3):154-164.
[12] SANDEEP G S,KUMAR B S S,DEEPAK D J. An Efficient Lossless Compression Using Double Huffman Minimum Variance Encoding Technique [C]//2015 International Conference on Applied and Theoretical Computing and Communication Technology (iCATccT).Davangere:IEEE,2015:534-537.
[13] 吴友情,张睿灵,汤进,等.定长编码和哈夫曼编码的密文域可逆信息隐藏 [J].中国图象图形学报,2022,27(1):277-288.
[14] 丁琳琳,李正道,纪婉婷,等.基于改进哈夫曼编码的大规模动态图可达查询方法 [J].电子学报,2017,45(2):359-367.
[15] 蔡春梅.哈夫曼编码方法的方案选择研究 [J].中国新通信,2013,15(7):73-74.
[16] 刘海峰,刘澄澄.基于VC++的无损压缩技术实现 [J].网络安全技术与应用,2019(6):38-41.
[17] 贾先韬,张旭,刘泽曦.基于verilog实现哈夫曼编码的新方法 [J].电子产品世界,2017,24(12):40-42+66.
[18] 杨兰.基于C语言的哈夫曼编码的实现 [J].软件导刊,2012,11(9):40-42.
[19] 王向鸿.基于Matlab文本文件哈夫曼编解码仿真 [J].现代电子技术,2013,36(20):31-32.
[20] CHENG K,SHEN Q,LIAO S K,et al. Implementation of Encoder and Decoder for LDPC Codes Based on FPGA [J].Journal of Systems Engineering and Electronics,2019,30(4):642-650.
[21] 邓家先,肖嵩,李英.信息论与编码:第三版 [M].西安:西安电子科技大学出版社,2016.
[22] 刘兴科,陈轲,于晓光.Huffman编码在矢量地图压缩中的应用 [J].测绘科学技术学报,2014,31(1):89-92.
作者简介:王梦梵(2002—),男,汉族,重庆人,本科在读,主要研究方向:数据结构。