摘" 要:针对协同过滤算法中存在的数据稀疏性、可扩展性及准确性问题,提出一种基于改进矩阵分解和谱聚类的协同过滤算法。该算法首先将通过抑制物品流行度和用户活跃度优化的相似度计算融入最小二乘法(ALS),以避免矩阵分解时因子信息的丢失;其次结合流形学习的谱聚类算法弥补ALS算法产生的大计算量问题,同时获得全局最优解以提高聚类所得目标用户最近邻居的准确率;最后利用Movielens数据集进行实验。实验结果表明,改进的算法可以有效降低协同过滤算法的平均绝对误差和均方根误差,提高准确率,拥有更优的性能。
关键词:协同过滤算法;相似度;谱聚类;全局最优解
中图分类号:TP391.3" 文献标识码:A" 文章编号:2096-4706(2024)09-0073-04
Collaborative Filtering Algorithm Based on Improved Matrix Factorization and Spectral Clustering
SHU Juelin, XIE Hongtao, YUAN Gongping
(CETC Big Data Research Institute Co., Ltd., Guiyang" 550002, China)
Abstract: A collaborative filtering algorithm based on improved matrix factorization and spectral clustering is proposed to address the issues of data sparsity, scalability, and accuracy in collaborative filtering algorithms. The algorithm first incorporates similarity calculation optimized by suppressing item popularity and user activity into the least squares method (ALS) to avoid the loss of factor information during matrix decomposition. Secondly, manifold learning algorithm based on spectral clustering is used to compensate for the high computational complexity caused by the ALS algorithm, while obtaining the global optimal solution to improve the accuracy of clustering the nearest neighbors of the target user. Finally, experiments are conducted using the Movielens dataset. The experimental results show that the improved algorithm can effectively reduce the average absolute error and root mean square error of the collaborative filtering algorithm, improve accuracy, and have better performance.
Keywords: collaborative filtering algorithm; similarity; spectral clustering; global optimal solution
0" 引" 言
互联网迅速发展的当下,其所含信息的增长情况表现为指数爆炸型增长趋势。如今,人们面临着各行各业的海量信息数据,如何从海量数据中选择有价值数据变得越来越重要。因此,个性化推荐系统应运而生,被广泛地用于信息过滤[1]。目前而言,被广泛应用于各领域的主流推荐系统算法为:混合推荐算法、协同过滤推荐算法和基于内容的推荐算法,其中协同过滤算法备受关注[2]。在协同过滤算法中,用户在过去对商品或项目的评分表现出较高的相似性,那么他们很有可能在未来对其他商品或项目也会有类似的评分倾向[3]。虽然协同过滤算法备受喜爱与关注,但是它仍存在一些问题,包括数据稀疏性、可扩展性和准确性等问题。首先,数据稀疏性问题指的是用户对物品的评分数据非常少,以至于评分矩阵非常稀疏,使得推荐系统在预测用户对未评分项目的喜好时面临困难,从而影响了推荐结果的准确性。其次,可扩展性问题指在处理大规模数据集时,算法需要计算用户之间或物品之间的相似度,这导致计算量急剧增加,可能会影响实时性和推荐质量。最后,准确性问题指的是在算法推荐的过程中,存在很多挑战,如冷启动、偏好漂移等,这些因素会对推荐结果的准确性产生影响。因此,在个性化推荐系统中,解决数据稀疏性、可扩展性和准确性问题是非常重要的。
为此许多学者作出了更多的研究并取得了相应的成果。文献[4]为了提高算法的推荐准确度,将用户或者物品的相似度计算融入目标函数进行训练,提高了准确度。文献[5,6]基于目标函数的相似性融合的方式,对ALS矩阵分解算法进行改进,以提高推荐的准确度。文献[7,8]提出将协调过滤算法结合聚类算法将用户通过群体划分的方法进行分类,以缩小搜索邻居用户的空间,提高算法的效率。通过对传统协同过滤算法存在的问题以及相关文献进行分析,发现这些改进算法仅仅针对目标函数融入相似性,没有进行相似度公式上的改进。而在协同过滤阶段采用K-means聚类时,由于K-means有着维度灾难问题,在处理大规模数据场景时,会造成计算复杂度高,进而影响推荐结果的准确性。因此,本文提出了一种基于改进矩阵分解和谱聚类的协同过滤算法,以解决稀疏性、可扩展性和准确性问题。该算法首先通过改进相似度计算方法来提高推荐的精确性。其次融合ALS矩阵分解的损失函数弥补矩阵分解时的信息丢失,以提高推荐准确率和解决稀疏性问题,之后再运用流形学习的谱聚类算法根据相似度对用户求解最近邻,最后求得推荐结果。
1" 算法理论
1.1" ALS矩阵分解算法
ALS矩阵分解算法实质上是基于矩阵奇异值分解原理的。它的目标是填充用户—项目评分矩阵中缺失的项目评分数据,通过将该矩阵拆解为两个矩阵相乘的形式来实现。定义用户对项目评分矩阵R = [ri, j]m×n:
ALS矩阵分解算法[9]主要是通过低维矩阵Xm×k和Yn×k相乘,逼近用户—物品评分矩阵Sm×n,即:
(1)
对高维Sm×n进行降维,得到Xm×k和Yn×k,分别是项目和用户的隐含特征矩阵,通常取 。由于ALS矩阵分解算法是通过交替最小二乘法填补评分矩阵[10],因此损失函数为:
(2)
其中,每个用户对应一个因子向量xi,每个用户对应一个因子向量yj,通过计算这两个因子的内积 ,可以得到用户i对项目j偏好评分的近似值。xij表示用户i对项目j的评分预测值,λ表示正则化项的系数,用于简单的防止模型的过拟合,提高模型泛化能力,并避免过度依赖训练数据。其求解方法如下:
首先固定项目特征矩阵Y,然后对误差损失函数L(X,Y)关于用户特征矩阵X的每个元素Xi求偏导,并令导数等于0,来求解最优的用户特征矩阵:
(3)
同理固定X,可得:
(4)
其迭代步骤是:首先,随机初始化项目特征矩阵Y。然后,使用式(3)更新用户特征矩阵X。最后,使用式(4)更新项目特征矩阵Y。直到满足收敛条件或达到最大迭代次数为止,以确定算法能够逐步优化模型参数并逼近真实评分矩阵的结果。
1.2" ALS矩阵分解算法的改进
Spark的ALS矩阵分解算法是混合推荐算法,可以基于物品或者用户进行推荐,但是ALS矩阵分解进行迭代填充用户—项目评分矩阵时,容易造成因子信息的丢失,从而影响推荐的准确度。因此本文通过对ALS的损失函数融入相似度,以弥补矩阵分解造成的误差。
1.2.1" 用户相似度的优化
关于相似度计算,传统的方法中没有考虑到物品流行度对用户相似度的影响。多个用户对大众必需品项目进行高评分,但是用户之间不一定有相似性。如果多个用户对小众某项目进行过高评分,那么用户之间更可能存在相似性。基于此,加入物品流行度的惩罚因子对修正余弦相似度公式进行改进,计算式为:
其中,1/(log1+r(s))表示物品流行度惩罚因子。
1.2.2" 物品相似度的优化
在修正的余弦相似度计算中,没有考虑用户活跃度对物品相似度的影响。假设部分相同的物品存在于很多用户的兴趣列表中,由此来证明这些物品具有大概率的相似性,可以认为在物品相似度计算时,每个用户的兴趣列表对推荐系统的贡献大小存在差异。因此在计算物品相似度时,对于活跃的用户的兴趣列表进行特殊处理。相比之下,评分项目较少的用户更有可能出于真正的兴趣进行评分,因此他们的兴趣列表对计算结果贡献较大。为了解决这个问题,在修正余弦相似度公式中引入了惩罚因子,用于衡量活跃用户对兴趣列表的贡献,其计算式为:
其中,1/(log1+r(i))表示用户活跃度的惩罚因子。
综上,在ALS矩阵分解算法中,加入物品和用户的相似度可以弥补因子信息丢失所导致的预测评分不准确问题,从而提高推荐结果的准确性。因此在损失函数中加入改进后的相似度理论,计算式为:
2" 实验设计
为了克服传统协同过滤算法的局限性,本文提出一种基于改进矩阵分解和谱聚类的协同过滤算法(ASCF+)。首先ASCF+算法通过引入流行度和活跃度因子,将它们融合到ALS(交替最小二乘)矩阵分解的损失函数中,从而更准确地计算物品之间的相似度。其次,为了弥补迭代计算时因子信息丢失的问题,ASCF+算法利用谱聚类中的降维技术来缓解传统K-means算法面临高维度矩阵的维度灾难问题。谱聚类是一种基于图论理论的聚类方法,它可以将高维数据映射到低维空间,并通过对低维空间中数据点进行聚类来得到最终结果。ASCF+算法借鉴了谱聚类的思想,利用降维技术来减少计算复杂度,提高算法的效率和准确性。具体步骤如下:
1)利用改进的ALS矩阵分解对高维稀疏的用户—项目评分矩阵R = [ri, j]m×n进行数据的填充得到稠密矩阵R′。
2)利用谱聚类对用户—项目评分数据进行聚类,最终把所有用户划分为k类。分别记为U1,U2,…,Uk,其中,Ui ∩ Uj = ∅,1≤i,j≤k,U1 ∪ U2 ∪…Uk = U。
3)根据步骤2)普聚类之后得到的相似用户,使用选定的相似度指标计算每对用户之间的相似度,并将结果存储在一个矩阵中,最终得到用户间的相似度矩阵A ∈ Rm×n,其中Ai, j = sim(ui,uj)。
4)根据用户间的相似度矩阵对稠密评分矩阵R′进行验证,以确定矩阵分解填充得到的评分是否正确。如果相似用户对某项目的评分是相近的,则说明评分准确,否则继续调整参数进行训练。
3" 实验结果及分析
3.1" 实验数据及评价指标
本实验使用GroupLens Research采集的电影评分数据MovieLens [11],进行算法模型的训练、参数调优和效果评估。因此把数据集划分为训练集、验证集和测试集。从数据集中随机抽取60%作为训练集,用于模型的训练;再从剩下的数据中随机各抽取20%作为验证集和测试集,用于确定最优参数和评估算法的效果。从而可以确保对算法模型进行全面的评估和比较。本文的实验平台为Windows 10,64位双核,IDE为IntelliJ IDEA,算法由Scala语言实现。
实验结果的评价指标使用MAE和RMSE。计算式分别为:
其中,G(i)表示用户ui已评分项目个数, 表示用户ui的预测评分,ri,t表示实际评分。
3.2" 实验结果及分析
3.2.1" 实验一
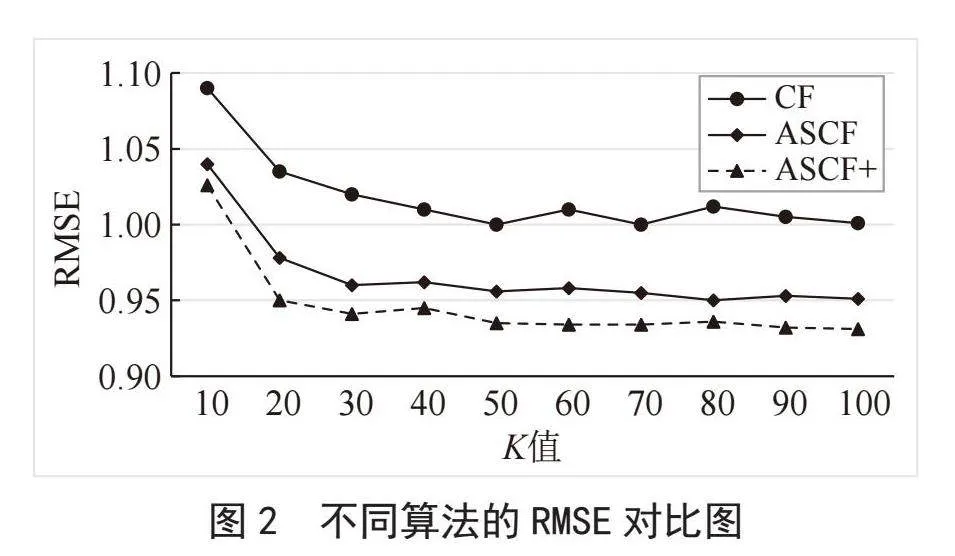
在MovieLens数据集中,本文选择了10个不同的K值(取自0到100之间)来测试改进的矩阵分解和谱聚类协同过滤算法(ASCF+)。同时,进行了与传统协同过滤算法(CF)和未改进矩阵分解和谱聚类的协同过滤算法(ASCF)的比较试验。具体对比结果如图1所示。
根据图1、图2可以看出,随着K值的增大,三种算法在Movielens数据集上的实验结果显示,MAE值和RMSE值呈现快速下降的趋势,但当K=30时,测试值逐渐趋于平稳。此外,改进矩阵分解的ASCF+算法相较于不改进矩阵分解的ASCF算法和传统CF算法,在MAE和RMSE值上表现更低,准确率也有所提高。
3.2.2" 实验二
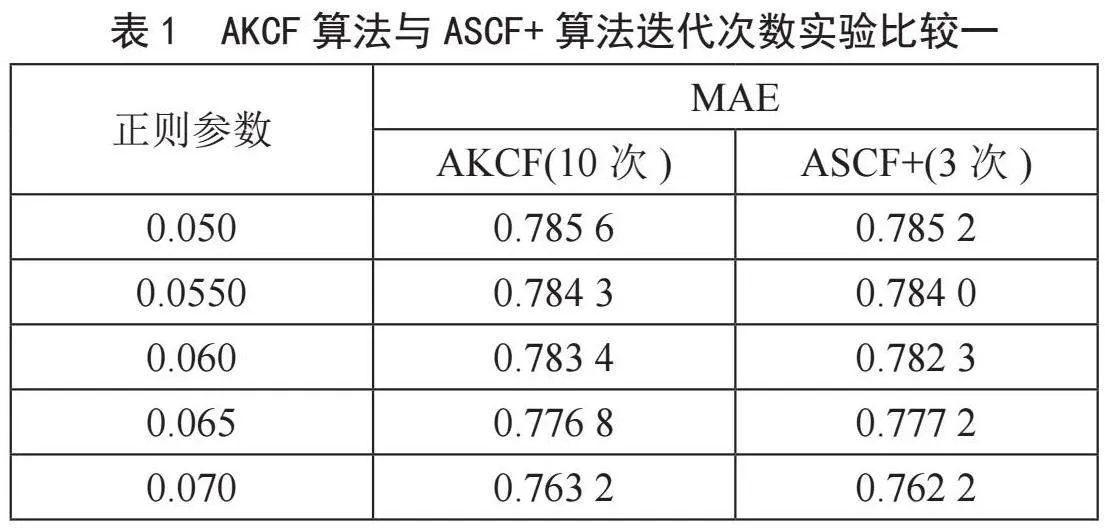
为了进一步验证本文算法的执行效率,设置不同正则参数,相同的K值下,选择平均绝对误差MAE作为评价标准,对比文献[7]的基于矩阵分解和聚类的协同过滤算法(AKCF)和本文改进算法的迭代次数。对比结果如表1所示。
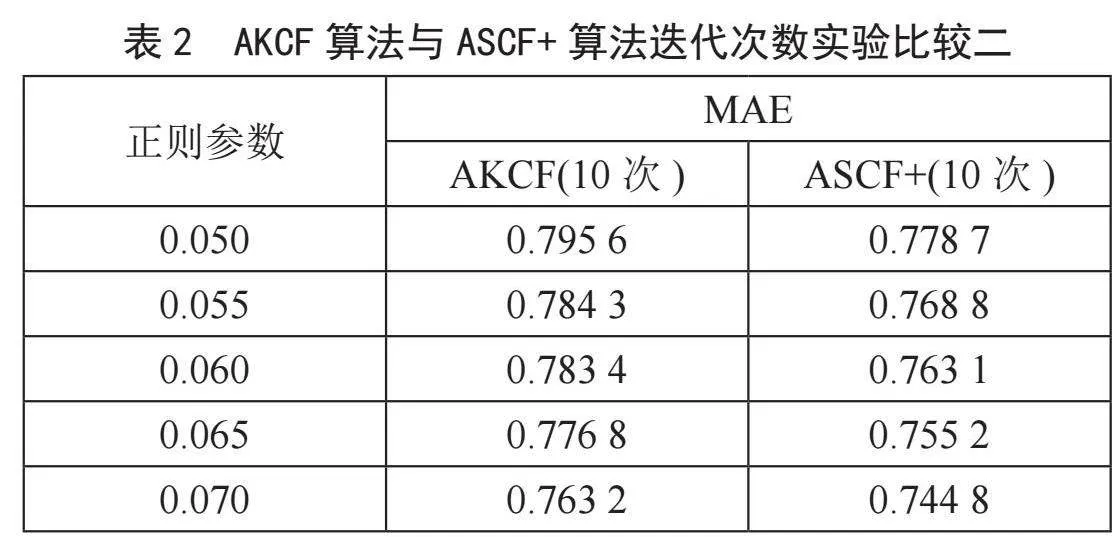
从表1中可以看出,ASCF+与AKCF算法的MAE值相近,但是迭代次相差倍数级别。因此,在相近的MAE值下,ASCF+算法收敛的速度更快,性能更优。因为ASCF+算法在协同过滤阶段采用了谱聚类,相对K-means聚类算法能够快速针对高维矩阵进行降维聚类。为进一步验证ASCF+算法的性能,本文将ASCF+算法迭代次数增加到10次,并再次进行比较,如表2所示。
由表2可以看出,把算法的迭代次数设置为10时,ASCF+算法在不同的正则参数下获得的平均绝对误差(MAE)值较AKCF算法小,这表明ASCF+算法在性能上更具优势。这是因为本文改进算法ASCF+在矩阵分解阶段的损失函数中加入用户和物品的相似度计算是有效的,能够提高准确度。
4" 结" 论
传统协同过滤算法在处理高维稀疏数据时存在数据稀疏性、可扩展性和准确性等问题。解决这些问题的关键是通过对高维稀疏矩阵进降维来准确地发现相似项,并进行进一步地推荐。因此本文提出了一种基于改进矩阵分解和谱聚类的协同过滤算法,首先通过考虑将抑制物品流行度和用户活跃度改进的相似度计算融入ALS矩阵分解,弥补矩阵分解时因子信息的丢失,提高准确度的同时解决数据稀疏问题,其次使用谱聚类算法中的降维技术处理高维度的用户物品评分矩阵以获取相似用户。最后将相似用户计算相似度矩阵与ALS矩阵分解得到的稠密矩阵做比较,以验证填充的评分是否正确,从而进行推荐。实验结果验证表明,相比较于传统的协同过滤算法,本文改进的算法在推荐准确率方面有着显著的提升。
参考文献:
[1] THROAT P B,GONDAR R M,BARVE S. Survey on Collaborative Filtering, Content-Based Filtering and Hybrid Recommendation System [J].International Journal of Computer Applications,2015,110(4):31-36.
[2] 吴湖,王永吉,王哲,等.两阶段联合聚类协同过滤算法 [J].软件学报,2010,21(5):1042-1054.
[3] GONG S J. A Collaborative Filtering Recommendation Algorithm Based on User Clustering and Item Clustering [J].Journal of Software,2010,5(7):745-752.
[4] VOZALIS M G,MARGARITIS K G. Applying SVD on item-based filtering [C]//5th International Conference on Intelligent Systems Design and Applications.Warsaw:IEEE,2005:464-469.
[5] 倪满满.基于ALS模型协同过滤推荐算法的优化 [J].计算机与现代化,2018(2):76-79.
[6] 王振军,黄瑞章.基于Spark的矩阵分解与最近邻融合的推荐算法 [J].计算机系统应用,2017,26(4):124-129.
[7] 董立岩,王宇,任怡,等.基于矩阵分解和聚类的协同过滤算法 [J].吉林大学学报:理学版,2019,57(1):105-110.
[8] 王永贵,宋真真,肖成龙.基于改进聚类和矩阵分解的协同过滤推荐算法 [J].计算机应用,2018,38(4):1001-1006.
[9] 郑凤飞,黄文培,贾明正.基于Spark的矩阵分解推荐算法 [J].计算机应用,2015,35(10):2781-2783+2788.
[10] LEGER D W,DIDRICHSONS I A. An Assessment of Data Pooling and Some Alternatives [J].Animal Behaviour,1994,48(4):823-832.
[11] GROUPLENS. MovieLens 100K Dataset [DB/OL].[2023-08-28].https://grouplens.org/datasets/movielens/100k/.
作者简介:舒珏淋(1992—),男,侗族,贵州镇远人,硕士在读,研究方向:数据挖掘。