

摘" 要:为了降低三相逆变电源的总谐波失真,提高动态响应能力,提出一种LC滤波型三相逆变器并设计有限集模型预测直接电压控制系统。首先,设计LC型滤波器并串接于三相逆变器输出端,以降低正弦电压的总谐波失真;接着,推导LC滤波型三相逆变器离散时间数学模型,预测逆变器系统在可能开关状态作用下的输出电压;然后,开发基于滤波电感电流和输出电压的负载电流估计策略,补偿预测模型中的未知负载电流;最后,构建成本函数作为最优开关状态选择标准。所提方法在MATLAB/Simulink中进行仿真验证,仿真结果证明了方法有效性。
关键词:模型预测控制;三相逆变器;LC型滤波器
中图分类号:TP241" 文献标识码: A" 文章编号:2096-4706(2024)09-0029-05
Finite-Control-Set Model Predictive Voltage Control for Three-phase Inverter with LC Filter
LIN Huawang
(Fujian Depco Power Generation Co., Ltd., Ningde" 352000, China)
Abstract: In order to reduce the total harmonic distortion of three-phase inverter power supply and improve the dynamic response capability, this paper proposes a three-phase inverter with LC filter and designs a finite-control-set model predictive voltage control system. Firstly, LC filter is designed and connected to the output of three-phase inverter in series to reduce the total harmonic distortion of sinusoidal voltage. Next, a discrete-time mathematical model of the three-phase inverter with LC filter is derived to predict the output voltage of the inverter system under possible switching states. Then, a load current estimation strategy based on the filter inductance current and output voltage is developed to compensate for unknown load current in the prediction model. Finally, a cost function is established as a criterion for selecting optimal switch states. The proposed method is simulated and validated in MATLAB/Simulink, and the results prove its effectiveness.
Keywords: model predictive control; three-phase inverter; LC filter
0" 引 言
三相逆变器广泛应用于光伏并网发电、风力发电等行业中[1]。其中,三相LC滤波型三相逆变器具有较低的电压电流总谐波失真,因此大量应用于不间断电源等要求高质量电压输出的场合。
LC滤波型三相逆变器增加了控制器设计和控制参数整定的难度。近年来,大量先进控制策略应用于这类逆变器系统,包括滑模控制[2]等非线性控制、比例积分控制等线性控制,无差拍控制[3]、重复控制[4]等。这些控制方法都需要一个调制模块,以生成驱动信号。
预测控制方法以其快速动态响应等优势受到电力电子领域的关注[5]。预测控制可以很直观地考虑系统约束、非线性和多变量问题,并且易于实现[6]。然而,预测控制具有计算量大的问题,导致早期在电力电子领域的应用受到限制。近几年来,随着微处理器的发展,预测控制在电力电子领域的潜力得以发掘。预测控制利用系统模型预测未来的系统状态,并根据预定义的成本函数获得优化控制行为[7]。在模型预测控制中,成本函数可以统一考虑不同的系统控制目标,并赋以权重因子[8]。构建成本函数时可以考虑采用不同的控制时域和预测时域,提高控制性能[9]。为了简化模型预测控制应用,三相逆变器建模为具有有限开关状态的系统,并考虑一步预测时域的优化问题。通过在线评估所有可能的开关状态,选择使成本函数最小的开关组合作用到三相逆变系统。
本文提出一种简单有效的LC滤波型三相逆变器模型预测控制策略。本控制器推导LC滤波型三相逆变器电气模型作为预测模型,并在每个控制周期计算所有可能的开关行为下,三相逆变系统的输出。在此基础上,构建成本函数作为下一时刻作用于系统的优化开关状态的选择标准。本模型预测控制策略不需要调制器,由控制系统直接生成门驱动信号。
1" 控制系统建模
1.1" LC滤波型三相逆变器数学模型
LC滤波型三相逆变器作为一种常见的电力电子设备,用于将直流电源转换为交流电源,以满足各种应用领域的电能需求。在当前的技术发展中,常用的逆变器拓扑之一是两电平功率电路。这种拓扑结构具有许多优点,包括简单、高效、可靠,因此在多种应用中得到广泛采用。基于两电平功率电路的LC滤波型三相逆变器如图1所示。两电平功率电路由三个半桥电路组成,通常是IGBT(绝缘栅双极型晶体管)或MOSFET(金属氧化物半导体场效应晶体管)。6个开关管控制着逆变器的输出,可以将电流和电压从直流到交流进行有效的切换。三相逆变器的开关状态可以表示为:
式中,Sa、Sb、Sc表示a,b,c桥臂的开关状态,并定义为:
且a = e j(2π/3)。因此,三相逆变器输出电压空间矢量可以表示为:
Vi = VDC S" " " " " " " " " " " " " " "(3)
式中,VDC表示直流母线电压。根据式(3),考虑所有可能的开关状态,可以得到8个电压矢量,如表1所示。从表1可见,由于V0 = V7,因此只有7个不同的电压矢量,如图2所示。
LC滤波器是一种重要的电子电路元件,通常用于消除电路中的高频噪声、波动和谐波成分,以提供更稳定的电流和电压输出。它由电感和电容两种元件组成,这两种元件各自具有特定的电性质,用于实现不同的滤波功能。电感元件主要特点是抵抗电流变化趋势,可以储存电能;电容元件主要特点是可以储存电荷,并具有对电压变化的快速响应。LC滤波器将电感和电容连接在一起,因此可以由电感和电容方程描述,如图3所示。滤波电感电流方程可以写为:
式中,if表示电感电流,Vc表示电容电压,L表示滤波电感值。电容电压方程可以写为:
式中,C表示电容值,io表示输出电流。令 ,,,,
则LC滤波器方程(4)和(5)可以重写为矩阵形式:
1.2" LC滤波器离散模型
在数字控制系统中,模拟信号通常以离散时间进行采样,控制算法通常是基于离散时间的,因此必须将LC滤波器方程转化为离散时间模型。根据前向欧拉公式,LC滤波器的离散模型可以写为:
式中,Ts是控制周期。
1.3" 输出电流估计
为了通过式(7)离散模型预测输出电压,必须已知输出电流io。然而,通常输出电流和负载是未知的。根据式(5),k-1时刻输出电流可以估计为:
由于预测系统控制频率相对输出电流变化频率快得多,可以认为k时刻和k-1时刻的输出电流是相等的,即:io (k - 1) = io (k)。
2" LC滤波型三相逆变器有限集模型预测控制系统
有限集模型预测控制具有快速动态响应的优点,非常适合三相逆变器等电力电子系统。式(7)预测所有可能开关矢量Vi,i = 0…7作用下,系统下一时刻的电压输出。本节将构建成本函数,选择优化开关矢量。为了最小化输出电压跟踪误差,成本函数定义为:
式中, 和" 分别表示参考输出电压的实部和虚部, 和" 分别表示预测输出电压的实部和虚部。
LC滤波型三相逆变器有限集模型预测控制系统框图如图4所示,通过电压传感器和电流传感器分别获得输出电压和滤波电感电流,并由式(8)估计输出电流,最后通过式(7)预测所有电压矢量作用下的k+1时刻的输出电压。构建式(9)成本函数,比较不同输出电压下成本函数大小,选择使成本函数最小的电压矢量为优化电压矢量,作用于三相逆变器。
3" MATLAB/Simulink仿真模型设计及结果分析
3.1" MATLAB/Simulink仿真模型设计
MATLAB在电力电子装置仿真中的广泛应用使其成为研究和验证新方法的重要工具[10]。本文为了验证所提出的控制方法的有效性,在MATLAB/Simulink环境中创建了一个仿真模型,该模型代表了一个LC滤波型三相逆变器,该逆变器连接到一个电阻负载。表2中列出了系统所使用的参数,这些参数包括电感、电容等,它们对于逆变器的性能起着重要作用。在该仿真模型中,采用了一个六个绝缘栅双极型晶体管的两电平逆变桥拓扑结构,以构建三相逆变器。此外,模型预测控制(MPC)算法是采用MATLAB中的m语言编写的,用于控制逆变器的运行。控制周期设置为0.000 05秒,这表示每隔0.000 05秒控制系统会重新计算并更新控制指令,以实现对输出电压的动态调整。此外,仿真模型的运行步长设置为0.000 000 1秒,确保对系统动态行为进行高分辨率的模拟。为了评估系统性能,研究人员使用MATLAB/Simulink的THD(Total Harmonic Distortion)模块,该模块用于计算相电压的总谐波失真值。总谐波失真度是一项重要的性能指标,它测量了输出电压中包含的谐波分量的程度。通过分析总谐波失真度,本文能够评估所提出的控制方法对于减小电压谐波失真的效果。THD定义为:
式中,,Vn表示n次谐波电压的有效值;VF表示基频电压的有效值。
3.2" MATLAB/Simulink仿真实验结果
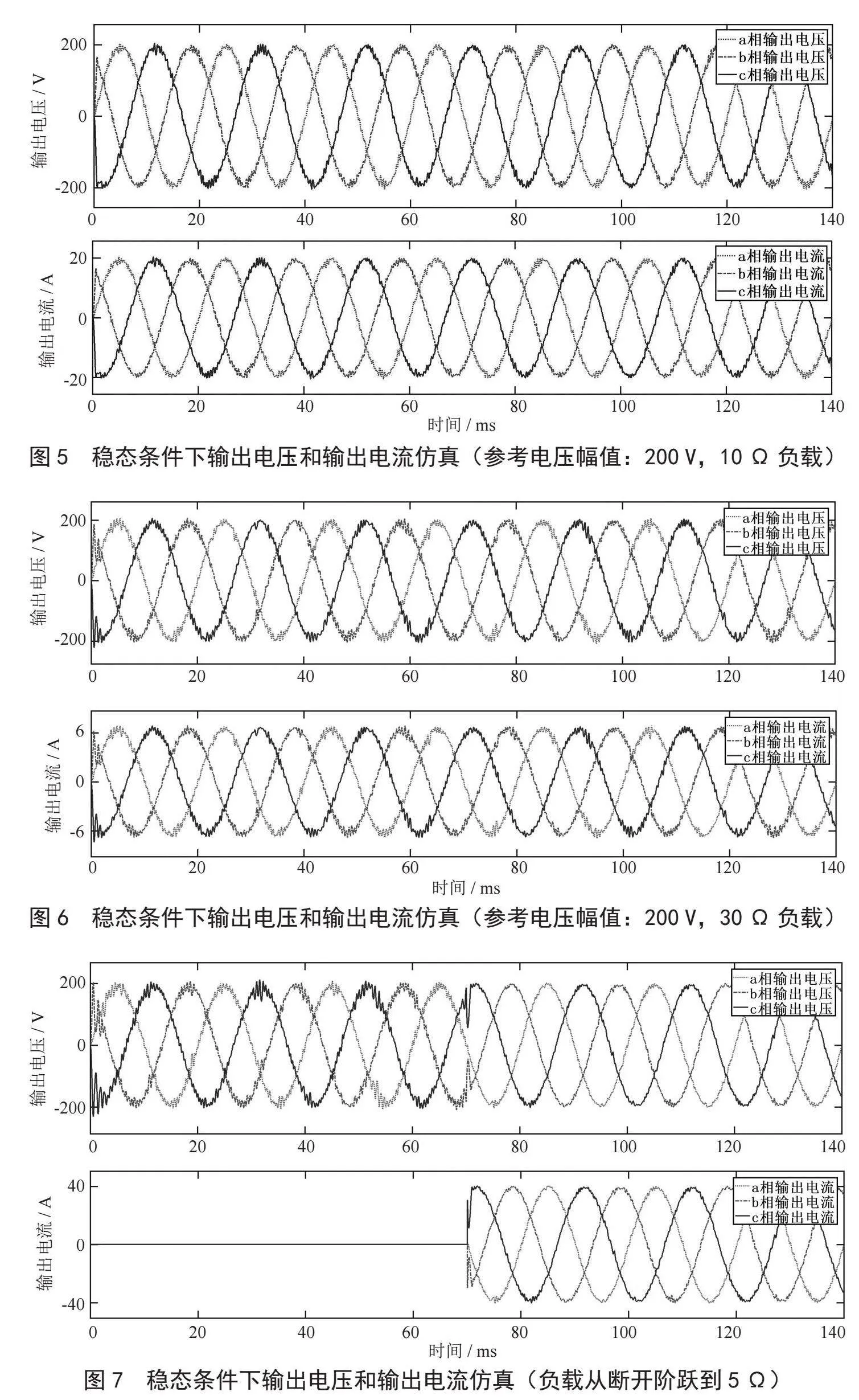
图5和图6提供了在不同负载条件下模型预测控制器在LC滤波型三相逆变器中的稳态性能评估。在本实验中,LC滤波型三相逆变器采用了模型预测控制系统,并在不同负载条件下进行了仿真评估。参考电压幅值被设置为200 V,工作频率为50 Hz,这是通常用于电力电子应用的标准值。首先,图5展示了当负载电阻为10 Ω时的性能评估结果。值得注意的是,输出电压呈现出非常稳定的正弦波形,这表明MPC控制系统能够准确跟踪参考电压,并维持输出电压的稳态。更令人鼓舞的是,总谐波失真度(THD)仅为4.5%。这意味着输出电压中包含的谐波分量非常小,符合高质量电压输出的要求。图6显示了在30 Ω负载下的性能评估结果。同样,逆变器输出的电压呈现出良好的正弦波形,并且THD仅为5.8%,表明系统在不同负载条件下都能保持较低的谐波失真度。此外,由于采用了纯电阻负载,负载电流与输出电压成正比,也呈现出正弦波形,这有助于减小系统对电网的干扰,提高了系统的电流质量。
图7提供了在负载阶跃变化条件下的LC滤波型三相逆变器输出电压和输出电流性能的评估结果。在本实验中,LC滤波型三相逆变器采用了预测控制系统,旨在评估其在负载瞬变情况下的性能。参考电压幅值被设定为200 V,工作频率为50 Hz,这是标准的电力电子应用参数。图7呈现了逆变器系统在不同负载条件下的响应。一开始,逆变器处于无负载状态,然后在0.07秒的时间点突然接入了5 Ω的负载。从仿真结果中可以明显观察到,在接入负载的瞬间,输出电压受到了影响,出现了短暂的波动。然而,值得注意的是,逆变器系统迅速恢复,并在大约0.7毫秒内重新稳定。这表明预测控制系统具有出色的动态响应能力,能够快速补偿电压的瞬时变化,维持系统的稳定性,并具有较小的总谐波失真。
4" 结" 论
本文提出一种LC滤波型三相逆变器有限集模型预测控制系统,利用一个离散预测模型计算控制变量预测值,无须整定参数。门驱动信号直接由控制器生成,因此不需要调制器。本预测控制策略采用无级联的单环结构,不需要内部电流环,因此极大提高电压控制的动态响应。本文对所提方法进行仿真,结果表明在电阻负载下,所提方法具有良好的电压控制性能。
虽然所提方法在MATLAB/Simulink仿真中具有优异的动态性能并获得较小的总谐波失真,但是抗干扰能力仍然不足。为了解决这个问题,拟从以下几个方面开展后续研究:
1)由于输出电流在模型中是未知的,本文采用基于滤波电感电流和输出电压的输出电流估计策略,然而其精度和抗干扰能力不足,后续将开展基于扰动观测器的电流估计策略研究,提高估计精度和鲁棒性;
2)本文成本函数直接采用参考值和预测值的误差构建,容易产生抖振问题,后续将开展新型成本构建策略,减小抖振,提高控制精度;
3)本文采用单时域的预测控制策略,控制精度和抗干扰能力受限,后续将开展多预测时域和控制时域的模型预测控制策略研究,进一步提高控制精度和抗干扰能力。
参考文献:
[1] 靳舵,张厚升,李家琪,等. 三相逆变器控制策略的研究与仿真分析 [J].实验室研究与探索,2022,41(11):114-118,217.
[2] 高兰香,赵兴勇,宋玲燕,等.基于滑模控制的光伏并网逆变器控制策略 [J].自动化与仪表,2022,37(11):37-43.
[3] 李圣清,姚鑫,冯浩田,等.基于复合预测的LCL型光伏逆变器无差拍控制 [J].湖南电力,2022,42(4):40-45.
[4] 梁欢,张琦,唐雨,等.用于并网逆变器谐波抑制的重复控制策略研究 [J].电力电子技术,2022,56(9):5-7+11.
[5] WANG Y,LIU F,CHEN S,et al. Prediction Errors Analysis and Correction on FCS-MPC for the Cascaded H-Bridge Multilevel Inverter [J].IEEE Transactions on Industrial Electronics,2022,69(8):8264-8273.
[6] 靳舵,张厚升,蒋俊杰,等.三相并网逆变器模型预测控制研究 [J].山东电力技术,2023,50(4):7-12.
[7] 任万英,许荷袖. 降低共模电压的三相逆变器模型预测控制策略 [J]. 电气传动,2020,50(11):40-46.
[8] ZHANG B,WU W,YANG Y,et al. A Novel Simplified Finite Control Set Repeat Model Predictive Control for Grid-Connected Inverters [J].IEEE Transactions on Industrial Electronics,2023,70(11):11324-11333.
[9] ESTRADA L,VAZQUEZ N,VAQUERO J,et al. Finite Control Set–Model Predictive Control Based On Sliding Mode For Bidirectional Power Inverter [J].IEEE Transactions on Energy Conversion,2021,36(4):2814-2824.
[10] 李璀璀,郑国庆,王景溢.基于MATLAB的半波整流电路仿真 [J].现代信息科技,2023,7(4):54-56+60.
作者简介:林华旺(1984—),男,汉族,福建宁德人,高级工程师,董事长,弱电系统福安市发电设备行业协会副会长,研究方向:电力电子及其控制技术。