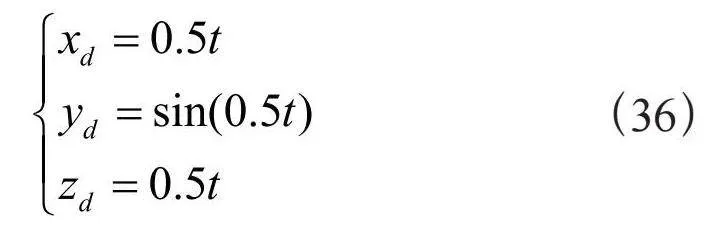



摘" 要:文章研究了自主水下航行器(AUV)的轨迹跟踪控制问题。为了提高自主水下航行器的轨迹跟踪性能,提出一种基于Lyapunov的模型预测控制(LMPC)方法来设计控制器。首先,基于该方法,考虑执行器饱和等实际约束,设计非线性反步跟踪控制律,在基于Lyapunov的模型预测控制问题中构造约束条件,使闭环的稳定性得到保证。其次,传统的控制器参数设置方法一般为试凑法,根据经验代入不同参数观察AUV的跟踪效果。对于其中的权重矩阵,采用改进的布谷鸟算法进行优化。最后,在MATLAB上的仿真结果表明,所提出的方法显著提高了AUV的轨迹跟踪控制性能。
关键词:自主水下航行器;轨迹跟踪;模型预测控制;布谷鸟搜索算法
中图分类号:TP18" " 文献标识码:A" 文章编号:2096-4706(2024)10-0188-06
Research on Trajectory Tracking Control of AUV Based on MPC
SHI Wenhui, JIN Lina, MA Nannan
(Liaoning Petrochemical University, Fushun" 113001, China)
Abstract: This paper investigates the trajectory tracking control problem of AUVs. In order to improve the trajectory tracking performance of AUV, a method of Model Predictive Control based on Lyapunov is proposed to design the controller. Firstly, based on the method, considering practical constraints such as actuator saturation, a nonlinear backstepping tracking control law is designed, and constraint conditions are constructed in the problem of Model Predictive Control based on Lyapunov to ensure the stability of the closed-loop. Secondly, the traditional method for setting controller parameters is generally the trial and error method, where different parameters are substituted based on experience to observe the tracking effect of AUV. For the weight matrix in the Model Predictive Control based on Lyapunov, an improved Cuckoo Search algorithm is used for optimization. Finally, the simulation results on MATLAB show that the proposed method significantly improves the trajectory tracking control performance of AUVs.
Keywords: Autonomous Underwater Vehicle; trajectory tracking; model predictive control; Cuckoo Search algorithm
0" 引" 言
自主水下航行器(AUV)是水下救援、油气勘探的重要载体[1]。由于其在各种潜艇项目中有大幅降低风险和运营成本的潜力,引起了工业界和学术界越来越多的关注[2]。AUV的模型具有非线性、不确定性和高耦合性,因此在研究AUV的相关问题中常采用欠驱动的形式。轨迹跟踪作为AUV控制研究的重要内容,其控制鲁棒性和运行稳定性有待提高。
近年来,在AUV的运动控制中经常用到反步控制、滑模控制(SMC)、PID控制、自适应控制和神经网络控制等。Cho等[3]采用反步法和时滞估计来设计AUV轨迹跟踪控制器,仿真结果表明AUV具有准确和鲁棒的跟踪性能。但是反步控制的参数调整比较困难。Wang等[4]利用鲁棒滑膜控制来实现AUV的航向控制,并通过强化学习来调整SMC的参数,取得了不错的效果。Xiong等[5]在设计AUV轨迹跟踪控制器时,将智能PID和PD前馈控制器相结合,取得更好的扰动抑制和初始跟踪误差补偿,但在控制低速时,会出现积分饱和问题,导致系统出现超调等问题。Cui等[6]将神经网络,加入自适应控制设计中。引入临界神经网络评估所设计的控制器的性能,在自适应控制中设计了补偿项。
与大多数传统的控制方法相比,模型预测控制(MPC)的显著特点在于它能够在控制器设计中处理系统约束。MPC可以通过预测未来系统状态和输出、及时处理实时干扰、确保跟踪性能和闭环系统稳定性来进行优化。Shen等[7]提出一种MPC方案来解决AUV平面轨迹的规划和跟踪问题,首次给出了基于MPC的AUV轨迹跟踪控制的稳定性条件,但是没有考虑在垂直方向的运动。Yan等[8]设计了一种新的基于MPC的双闭环轨迹跟踪方法。外环控制器产生的速度传递给内环控制器,内环控制器产生控制输入,确保闭环轨迹跟踪。明确考虑了系统输入和状态的约束,提高了AUV的稳定运行能力。Zhang [9]提出一种以速度增量为控制输入,同时考虑输入约束和状态约束的模型预测控制器,验证MPC是一种基于优化的时域控制方法,以运动学为框架设计了一种控制器,通过速度反向寻求控制力。一方面,控制力不利于作用在推进器上;另一方面,这种控制器设计缺乏稳定性证明。
本文针对AUV的轨迹跟踪控制问题,提出一种基于Lyapunov的非线性模型预测控制(LMPC)方案。LMPC能够很好地处理非线性和交叉耦合的系统动力学以及推力限制方面的系统约束[10]。它避免了标准模型预测控制所需要的局部线性化,以相对简单的方式保证了闭环稳定性,对于推力分配问题,协调推进器生成跟踪控制律要求的广义力和力矩。利用基于Lyapunov的反步技术在LMPC问题公式中构造收缩约束,从理论上保证了所提出的LMPC控制算法的闭环稳定性。利用改进的布谷鸟搜索算法对LMPC权重矩阵进行寻优处理[11],将轨迹跟踪误差的绝对值作为其目标函数,寻找最佳的权重矩阵,使AUV能够较好的跟踪期望轨迹。
1" AUV模型
首先对AUV的坐标系进行说明,固定坐标系和随体坐标系如图1。固定坐标系是对地坐标系,原点为地球中的某一点。随体坐标系主要针对AUV坐标系,其原点为AUV的重心。
实验对象是Saab SeaEye Falcon,假设Saab SeaEye Falcon质量均匀分布,由于推力器布局不允许对横摇和俯仰运动进行主动控制,因此我们研究Falcon的进退、横移、潜浮和转艏四自由度轨迹跟踪控制。
AUV的运动学模型为:
式中, 表示AUV在固定坐标系下的位置和航向, 表示AUV在随体坐标系下的速度和偏航角速度。J(ψ)是取决于航向ψ的旋转矩阵。J(ψ)的形式为:
AUV的动力学模型为:
式中, 表示广义推力和力矩。 表示包含附加质量的惯性矩阵;C(v)表示科里奥利和向心矩阵;D(v)表示阻尼矩阵。
g(η)表示恢复力。广义推力τ是由五个推力器" 产生的,遵循 。其中,α表示在随体坐标系中推进器的方位矢量。对于猎鹰,方位角是固定的。因此,有推力分布:
式中,N是一个常数输入矩阵。
根据式(1)(3)和(6)可知AUV的模型可以表示为:
式中,状态定义为 ,控制定义为 。
在控制器设计中有如下假设:
假设1:科里奥利和向心矩阵是斜对称的: ;
假设2:阻尼矩阵是正定的:;
假设3:输入矩阵" 是非奇异;
假设4:所有推进器的容量都一样即:,i = 1,2,3,4,5。
2" 相关算法介绍
2.1" 模型预测控制算法
在控制过程中,存在一条轨迹作为跟踪对象。如图2所示,k为当前时刻。控制器通过当前AUV状态测量值和预测模型,预测未来一段时域[k,k + Np]系统的输出。通过求解满足目标函数及各种约束的优化问题,得到[k,k + Nc]内的一系列控制变量序列,并将该时控制序列中的第一个元素作为被控对象的实际控制量,当来到下一时刻k + 1时重复上述过程。如此滚动的完成优化问题,实现对被控对象持续控制。
2.2" 改进的布谷鸟搜索算法
布谷鸟搜索算法是一种基于群体智能的优化算法,模拟了布谷鸟寄生在其他鸟巢中产卵的行为。原始布谷鸟搜索算法通过式(8)来更新巢穴位置:
式中,n表示比例因子,是(0,1)的均匀分布随机数,post, j、post, k表示t代中的两个随机解。在改进的布谷鸟搜索算法中,通过式(9)来更新位置矩阵为nestN×Di的位置:
式中,种群规模为N,维度为D,每个维度的上、下限分别为upN×Di、lowN×Di;
在目标函数中,权重矩阵Q、R、P影响着AUV轨迹跟踪效果。因此,需要设置合适的Q、R、P,使得AUV达到较好的跟踪效果。传统的控制器参数设置方法一般为试凑法,根据经验代入参数值来观察AUV的跟踪效果。由于改进的布谷鸟搜索算法寻优精度、搜索活力较高。因此,这里我们使用改进的布谷鸟算法搜索合适的控制器权重矩阵的值。改进的布谷鸟搜索算法总结如下:
1)初始化。定义目标函数,将AUV轨迹跟踪误差的绝对值作为其目标函数,设置种群规模N = 100、搜索空间维数为21、最大发现概率Pa = 0.25、最大迭代次数为300,并随机生成巢穴初始位置;
2)根据莱维飞行产生新的巢穴位置,保留适应度最高的巢穴位置;
3)选择更新。丢弃不好的巢穴位置;计算目标函数的适应度值,将适应度较好的巢穴保留到下一代;
4)逐维更新。对步骤3)中保留下来的解,进行逐维学习。更新当前最优函数解并保存进化信息,记录最优解;
5)结束判决。判断当前解的质量是否满足算法结束条件,若满足算法结束条件,则结束,输出最终的解;否则返回步骤2),直到满足算法结束条件时为止。
3" 控制器设计
在AUV的轨迹跟踪控制中,给定一个期望轨迹re(t) + [xd(t),yd(t),zd(t)]T,定义了AUV的位置。假设期望轨迹re(t)及其导数是光滑有界的(至少有二阶导数)。根据期望轨迹计算出AUV的期望状态值如式(10)所示:
式中,ud表示期望纵向速度;rd表示期望偏航角速度;wd表示z轴方向的速度;ψd表示期望偏航角。
同时,假设" 符合动力学方程(3),可有:
得到参考控制力 。
式中, 可通过对(7)求时间导数来计算。此外,由于满足假设3,利用Moore-Penrose伪逆实现来解决推力分配子问题,得到各推进器的参考控制:
3.1" 非线性反步控制器
需要找到一个状态反馈控制器以及相应的Lyapunov函数在原MPC公式中添加收缩约束来实现LMPC问题。针对AUV轨迹跟踪问题,利用反步法设计基于Lyapunov的非线性控制器。定义如下变量:
式中, 表示位置跟踪误差。通过运动学方程(1),可得到:
将v作为轨迹跟踪控制的虚拟控制量:
令 ,然后将其代入式(16)(17)可得:
首先选取李雅普诺夫函数为:
式中, 其是指定的控制增益矩阵。对Lyapunov函数求导可得:
进一步构造Lyapunov函数候选:
式中,:
对V2求导:
将动力学方程(3)代入可以得到:
式中,,:
通过假设1,可以证明 。
因此,选择以下控制律:
其中,Kd>0。
将式(24)代入式(22)可得:
根据假设2,可以得到 。然后根据标准Lyapunov参数,式(24)下的闭环系统对于平衡" 是全局渐近稳定的。
3.2" 模型预测控制器设计
3.2.1" 非线性状态空间方程
根据前面的推导,可得到系统的非线性状态方程为:
式中,。
然后对预测模型进行离散化。离散化后的状态方程为:
其中,fd表示f离散化后的函数。
3.2.2" 目标函数
其中, 表示预测控制" 的预测状态; 表示状态误差, 表示控制误差;Np表示预测时域,Nc表示控制时域;权重矩阵Q、R、P是正定的;目标函数的第一项表示AUV跟踪上期望轨迹的能力。第二项是控制输入惩罚项,用来限制控制输入的变化范围。第三项是终端代价项,以在有限时间内将系统状态推向最优稳态。
3.2.3" 约束项
在对目标函数进行求解时,还需要满足下列约束。
控制量约束:
控制增量约束:
系统输出量约束:
对于AUV非线性系统,采用标准的MPC设计技术,需要进行局部线性化,以选择合适的加权矩阵并构造辅助的反馈控制律。为了避免局部线性化,同时保证MPC跟踪控制的闭环稳定性,设计辅助的基于Lyapunov的非线性跟踪控制律,作为收缩约束添加在原MPC公式中来实现LMPC问题。
其中,h(·)表示辅助的基于Lyapunov的非线性跟踪控制律,V(·)对应的Lyapunov函数。收缩约束的存在能够证明LMPC控制器继承了状态反馈控制 的稳定性属性。
3.3" 模型预测控制稳定性分析
LMPC算法下的闭环系统相对于平衡点" 渐近稳定,即在基于LMPC的轨迹跟踪控制下,AUV将收敛到期望轨迹。
证明:由于有(21)中的李雅普诺夫函数V2,连续可微且根本无界,由逆李雅普诺夫定理[13],存在函数 ,i = 1,2,3,它们属于" 类,使得下列不等式成立:
根据式(32),并且每次对一个采样周期执行最优解 ,有:
通过Lyapunov论证,可以得出LMPC算法下的闭环系统是渐近稳定的。
4" 仿真实验与分析
为验证本文所提出的基于Lyapunov的模型预测控制方法对时变轨迹的跟踪控制,在MATLAB上对正弦函数进行仿真实验。仿真中所用到的模型参数和水动力阻尼系数都是基于Falcon。
用正弦函数来测试AUV的跟踪控制:
对于LMPC控制器,使用以下参数:采样周期δ = 0.1秒;预测范围为T = 5δ;控制增益Kp = Kd = diag(1,1,1,1)。初始位置设置为[x,y,z,ψ]T = [2,-0.3,0,0]T,初始速度设置为[u,v,w,r]T = [0.1,0,0,0]T。
每个推进器的极限是500 N。由改进的布谷鸟搜索算法寻找的权重矩阵为:
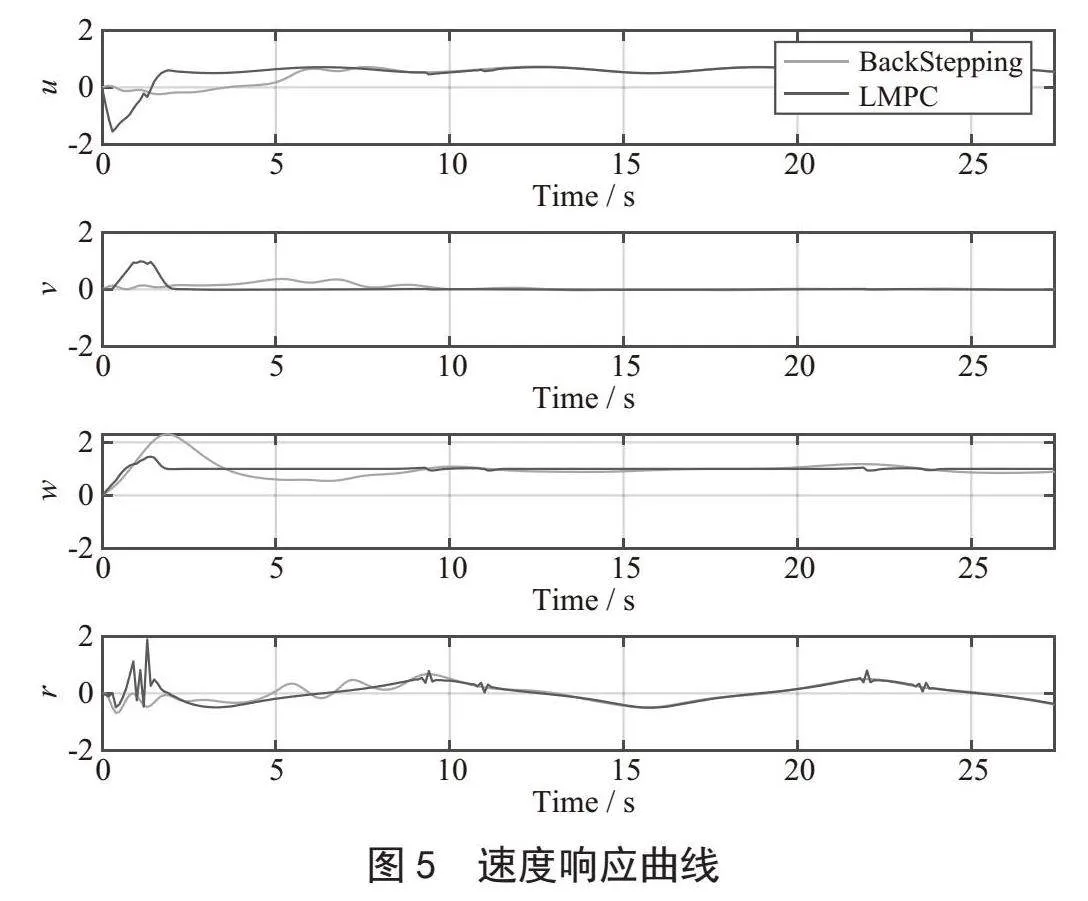
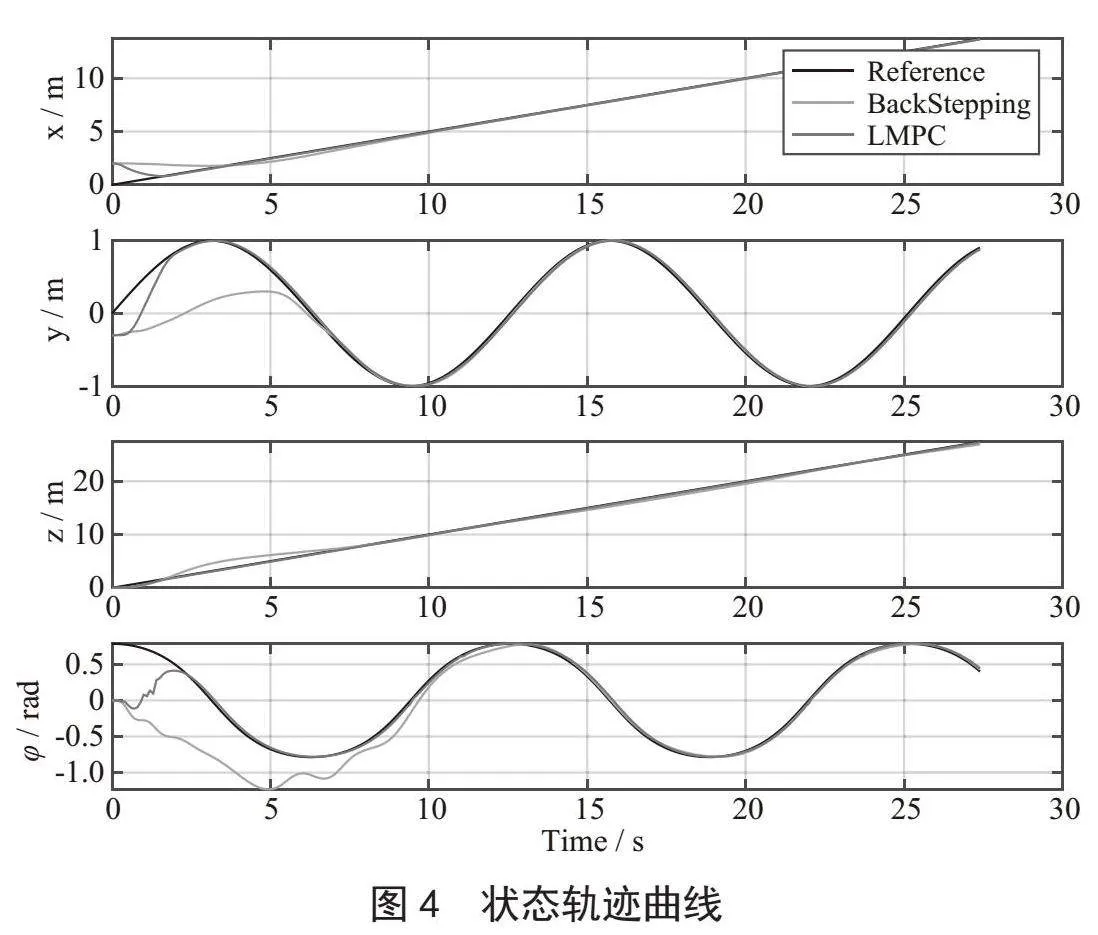
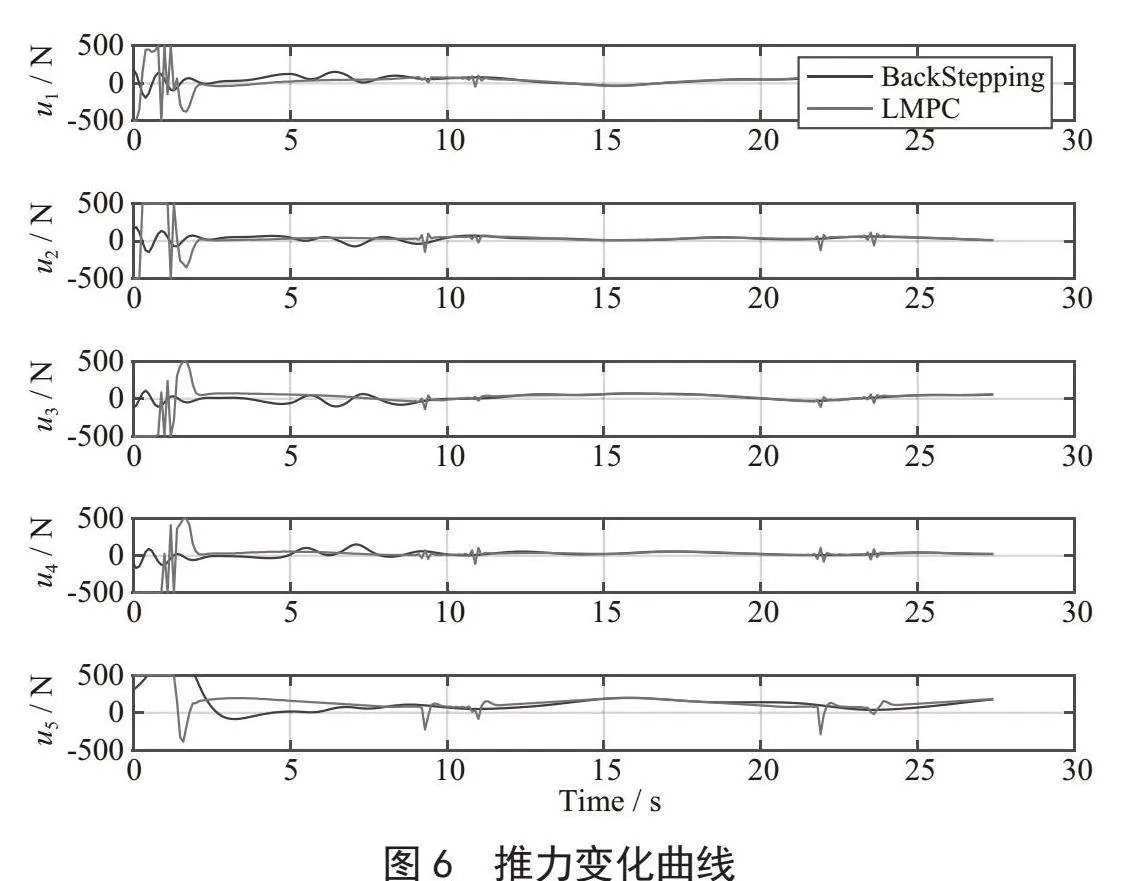
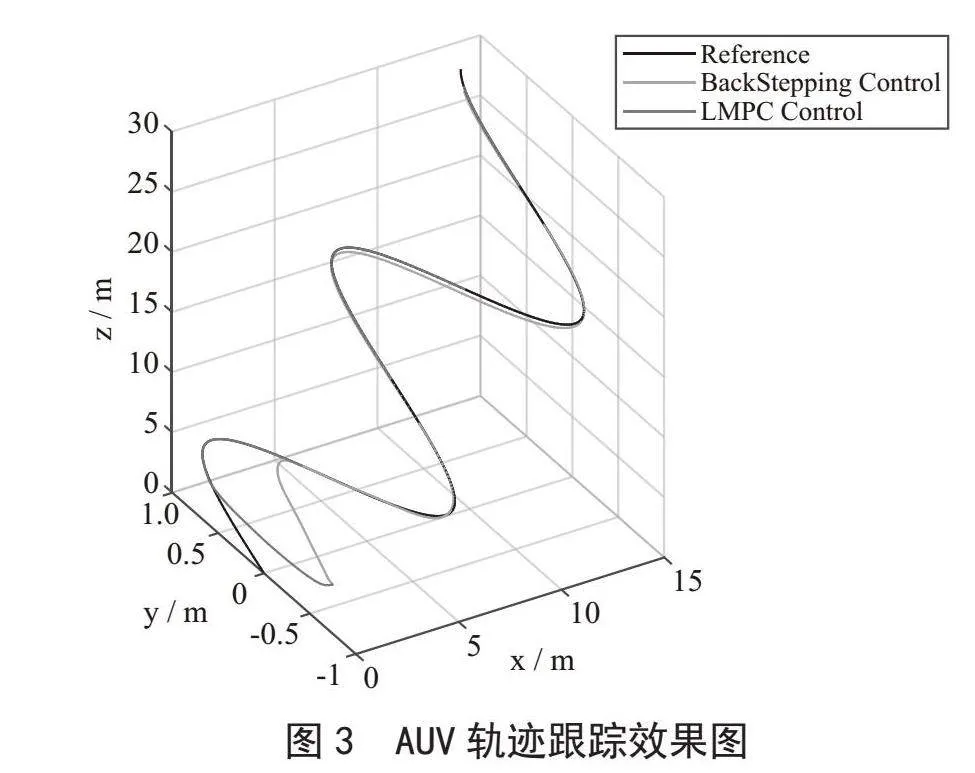
轨迹跟踪结果如图3所示。分别为采用反步控制(BSC)的AUV仿真轨迹,采用LMPC控制的轨迹,以及期望轨迹。从图中可以看出,BSC和LMPC都可以将AUV驱动到期望的轨迹,验证了闭环稳定性。但显然LMPC控制器的收敛速度比BSC控制器快得多。仿真结果验证了在线优化后跟踪控制性能的提高。从图4可以看出刚开始时初始位置与期望位置相差较大,随着AUV的调整,误差逐渐较小,实现精确的轨迹跟踪。图5为轨迹跟踪中的速度响应曲线。每个推进器所需的控制力如图6所示。我们观察到,在跟踪开始时,LMPC控制器充分利用机载推力能力,以产生尽可能快的收敛,同时尊重推进器的物理极限,推力的大小保持在预期的允许范围内。
5" 结" 论
在本文中,提出了一种新的LMPC算法用于自主水下航行器的轨迹跟踪控制,对于控制器中的参数,利用改进的布谷鸟算法对其进行优化,可以大大提高控制性能和鲁棒性。此外,推力分配子问题不需要单独考虑,因为在线优化允许它与LMPC控制器设计同时求解,严格证明了LMPC控制的闭环稳定性。对参考轨迹的跟踪仿真结果表明了所提出的基于LMPC的轨迹跟踪控制的优越性。
参考文献:
[1] 康帅,俞建成,张进.微小型自主水下机器人研究现状 [J].机器人,2023,45(2):218-237.
[2] 宋保维,潘光,张立川,等.自主水下航行器发展趋势及关键技术 [J].中国舰船研究,2022,17(5):27-44.
[3] CHO G R,LI J H,PARK D,et al. Robust Trajectory Tracking of Autonomous Underwater Vehicles Using Back-Stepping Control and Time Delay Estimation [J/OL].Ocean Engineering,2020,201:107131.(2020-03-05).https://doi.org/10.1016/j.oceaneng.2020.107131.
[4] WANG D,SHEN Y,WAN J,et al. Sliding Mode Heading Control for AUV Based on Continuous Hybrid Model-Free and Model-Based Reinforcement Learning [J/OL].Applied Ocean Research,2022,118:102960(2021-12-13).https://doi.org/10.1016/j.apor.2021.102960.
[5] XIONG Y,PAN L,XIAO M,et al. Motion Control and Path Optimization of Intelligent AUV Using Fuzzy Adaptive PID and Improved Genetic Algorithm [J].Mathematical Biosciences and Engineering,2023,20(5):9208-9245.
[6] CUI R,YANG C,LI Y,et al. Adaptive Neural Network Control of AUVs with Control Input Nonlinearities Using reinforcement learning [J].IEEE Transactions on Systems, Man, and Cybernetics: Systems,2017,47(6):1019-1029.
[7] SHEN C,SHI Y,BUCKHAM B. Integrated Path Planning and Tracking Control of an AUV: A Unified Receding Horizon Optimization Approach [J].IEEE/ASME Transactions on Mechatronics,2016,22(3):1163-1173.
[8] YAN Z,GONG P,ZHANG W,et al. Model Predictive Control of Autonomous Underwater Vehicles for Trajectory Tracking with External Disturbances [J/OL].Ocean Engineering,2020,217:107884(2020-08-06).https://doi.org/10.1016/j.oceaneng.2020.107884.
[9] ZHANG Y,LIU X,LUO M,et al. MPC-Based 3-D Trajectory Tracking for an Autonomous Underwater Vehicle with Constraints in Complex Ocean Environments [J/OL].Ocean Engineering,2019,189:106309(2019-08-23).https://doi.org/10.1016/j.oceaneng.2019.106309.
[10] 赵洪坛,朱大奇.UUV水下模型预测滑模跟踪控制算法 [J].控制工程,2022,29(7):1195-1203.
[11] 黄闽茗,何庆,文熙.基于逐维反向学习的动态适应布谷鸟算法 [J].计算机应用研究,2020,37(4):1015-1019.
作者简介:石文会(1997—),女,汉族,河南周口人,硕士在读,研究方向:无人水下航行器的轨迹跟踪控制;金丽娜(1985—),女,汉族,辽宁大连人,讲师,博士,研究方向:多智能体非线性控制;马楠楠(1997—),女,汉族,河南南阳人,硕士在读,研究方向:机器学习、机器人协同控制。

