

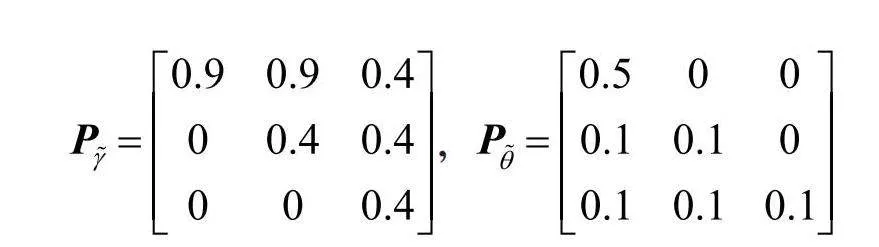
摘" 要:为了处理系统验证中大量存在的不确定性,国内学者将可能性理论引入到模型检测中,提出了广义可能性Kriple结构。广义可能性Kriple结构有着较好的应用前景,但有许多问题需要解决。其中的一个问题是,如何高效便捷地建立广义可能性Kriple结构的数学模型。为了给广义可能性Kriple结构中的模糊事件提供一种便捷方便的建模方法,在建模的过程中引入具有三种否定的广义模糊集(Generalized Fuzzy Sets with Contradictory, Opposite and Medium negation, GFScom),给出了广义可能性Kriple结构中的模糊事件的建模方法。应用实例表明所提方法是有效、可行的。
关键词:模糊事件;广义可能性Kriple结构;广义模糊集GFScom
中图分类号:TP301" 文献标识码:A" 文章编号:2096-4706(2024)12-0052-04
Event Modelling Method in Generalized Possibilistic Kriple Structure Based on GFScom
ZHANG Shengli1, CHEN Jing2, WU Jiao1,3
(1.School of Information Technology, Minzu Normal University of Xingyi, Xingyi" 562400, China;
2.School of Economics and Trade, Minzu Normal University of Xingyi, Xingyi" 562400, China;
3.School of Education, Guizhou Normal University, Guiyang" 550025, China)
Abstract: In order to deal with the abundance of uncertainties present in the system validation, domestic scholars introduces the possibility theory to the model checking and proposes the Generalized Possibilistic Kriple Structure (GPKS). The GPKS has a good application prospect, but there are many issues that need to be solved. One of the problems is how to efficiently and easily build mathematics model of the GPKS. In order to provide a convenient modeling method for fuzzy events in the GPKS, three Generalized Fuzzy Sets with Contradictory, Opposite and Medium negation (GFScom) are introduced in the process of modeling, and the modeling method of fuzzy events in the GPKS is given. Application examples show that the proposed method is effective and feasible.
Keywords: fuzzy event; Generalized Possibilistic Kriple Structure; generalized fuzzy sets GFScom
0" 引" 言
可能性理论[1]是一种处理不完备信息的不确定理论。正如文献[2]中所说,可能性理论与概率论不同,它不具有可加性。模型检测是一种形式化验证技术,已被应用于计算机硬件、通信协议、控制系统、安全认证协议等方面的分析与验证中[3]。近年来,尽管模型检测理论在形式化验证中日益重要,但经典的模型检测无法处理系统中不确定信息验证问题,尤其是模糊性信息的验证问题。为了处理系统验证中大量存在的不确定性,李永明等将可能性理论引入到模型检测中,提出了广义可能性Kriple结构,取得了一系列成果[4-7]。尽管广义可能性Kriple结构有着较好的应用前景,但仍有许多问题需要解决。其中的一个问题是,如何高效便捷地建立广义可能性Kriple结构的数学模型。
不确定信息的处理一直是知识处理领域非常重要的研究方向。近年来,国内外一些学者提出在不同领域中特别是模糊知识处理领域需要不同形式的否定。Wager [8]、Analyti [9]、Kaneiwa [10]和Ferré [11]在不同的知识领域给出了至少2种不同形式的否定。潘正华等认为模糊知识中的“否定”可以区分为矛盾否定、对立否定与中介否定,建立了模糊集FScom [12-14]。我们从哲学、语言学等角度出发,提出了广义模糊集,见文献[15,16]。如我们所知,建立广义可能性Kriple结构的模型是一件比较困难的事情,而基于广义模糊集合GFScom,我们可以方便高效地建模。
1" 广义可能性Kriple结构
定义1 [5,6,17]一个广义可能性Kriple结构(Generalized Possibility Kriple Structure, GPKS)是一个五元组M = (S,P,I,AP,L),其中:
1)S是可数的非空状态集。
2)P:S×S→[0,1]是广义可能性迁移分布函数,满足对于任何状态s,。
3)I:S→[0,1]是广义初始分布函数,满足 。
4)AP是原子命题集。
5)L:S→[0,1]AP是一个广义标签函数,其中[0,1]AP表示AP的所有模糊子集。
如果集合S和AP都是有限集,则称广义可能性Kriple结构M = (S,P,I,AP,L)是有限的。
注1:为了与模糊离散事件系统[18,19]中的模糊事件建立起关联,同时也为了阐述上的便捷,广义可能性迁移分布函数可以看作在某一模糊事件作用下迁移分布,譬如,与模糊事件" 相关联的广义可能性迁移分布P可以表示为 。类似,用" 表示与模糊事件" 相关联的广义标签函数, 则表示与模糊状态" 相关联的原子命题A。
例1 图1给出了一个广义可能性Kripke结构M = (S,P,I,AP,L),其中,用圆圈表示状态,用带标签的箭头表示迁移,且AP = {A,B}。在圆圈外标注状态名,具有隶属度的原子命题标注在圆圈内。一个没有源的输入箭头来表示初始状态。状态空间为S = {s0,s1,s2,s3};初始状态集只包含一个状态s0,使得I (s0) = 1。可能性迁移分布为P (s0,s1) = 0.8,P (s0,s2) = 0.4,P (s1,s2) = 1,P (s1,s3) = 0.7,P (s2,s1) = 0.6,P (s2,s3) = 0.9和P (s3,s3) = 1。广义标签函数为L (s0,A) = 0.8,L (s0,B) = 0.4,L (s1,A) = 0.6,L (s1,B) = 0.5,L (s2,A) = 0.4,L (s2,B) = 0.7,L (s3,A) = 0.1和L (s3,B) = 0.9。接着,可能性迁移分布P:S×S→[0,1]用模糊矩阵(P(s,t))s, t∈S表示。类似地,初始分布I:S→[0,1]和广义标签函数L:S→[0,1]AP可以分别表示为一个向量(I(s))s∈S和模糊矩阵(L(s,A))s∈S, A∈AP。使用状态序列s0<s1<s2<s3和原子命题符号序列A<B,为简单起见,用P表示矩阵(P(s,t))s, t∈S,I表示向量(I(s))s∈S,L表示矩阵(L(s,A))s∈S, A∈AP,则:
2" 基于GFScom的GPKS种事件建模
如何确定模糊事件下原子命题集AP的所有模糊子集的隶属度函数,即如何确定广义标签函数L。众所周知,要给出一个模糊原子命题A的合适有效的隶属度函数是非常困难的,然而在一些实际应用系统中,存在着成百上千个不同的模糊子集(分别对应不同的模糊原子命题),这是系统设计人员较为头疼的问题。下面,我们将基于广义模糊集合GFScom给出一种有效且简单的确定隶属度的方法。
2.1" 广义模糊集GFScom
根据GFScom [15,16],经过有限数值化映射后,任何论域都可以变换为一有限数值集。令U为有限数值集,F(U)表示U上所有模糊子集构成的集合,假设A ∈ F(U),a、b分别为U的左右端点,∀u ∈ U,*为t-模,n为补算子,则:
1)A的n矛盾否定集,定义为满足A¬(u) = n(A(u))的映射A¬:U→[0,1]所确定的模糊子集,记作A¬。特别地,如果n为线性补,那么A¬(u) = n(A(u)) = 1 - A(u)确定的模糊子集称为A的矛盾否定集。
2)A的对立否定集,定义为满足条件A¬(u) = A(a + b - u)且A¬(u) + A(u)≤1的映射A¬:U→[0,1]所确定的模糊子集,记作A¬。
3)A的*-n中介否定集,定义为满足A~(u) = A¬(u) * (A¬)¬(u) = n(A(u)) * n(A¬(u)) = n(A(u)) * n(A(a + b - u))的映射A~:U→[0,1]所确定的模糊子集,记作A~。特别地,如果t-模*为min,n取线性补,则称A~(u) = min{1 - A(u),1 - A(a + b - u)}为A的中介否定集。
2.2" 模型建立的过程
在下面的研究中,只考虑单个的广义模糊子集的情况,即AP中的每个原子模糊命题a都属于同一广义语言变量的项集。给定一个模糊事件,所有原子命题对所有状态的隶属度的计算方法可以被描述为以下三个步骤:
1)选择一个合适的有限数值化映射f,它将状态空间S映射到一个有限的数值集D。
2)根据实际经验确定某些(几个)适当的原子命题的隶属度函数,一般来说,隶属函数与状态有关。
3)利用广义模糊集GFScom和适当的语言修饰词[20]计算其他原子命题的隶属函数。
显然,上述计算过程适用于多个广义模糊子集和多个模糊事件。事实上,人们可以简单地重复上述计算过程。
3" 实例分析
如我们所知,在真实世界的复杂系统中,模糊性、不精确性和主观性是其典型特征。因此,采用GFScom对广义可能性Kriple结构中的模糊事件进行建模,可以较好地处理真实世界复杂系统中模糊性问题。
例2 [7]假设有一只动物患上了一种新的疾病。对于这种新疾病,医生对它并不完全了解,但他(或她)根据经验相信这些药物,如茶碱、异丙托溴铵、琥珀酸红霉素乙酯和多巴胺(分别记为 ,, 和 )可能对该疾病有用。
为简单起见,我们假设医生认为动物的状况大致有三种状态,即“good”“fair”和“poor”。如我们所知,当动物的状态被称为“good”“fair”和“poor”时,它是模糊的,因为在现实生活中,动物的状态可以同时属于“good”“fair”和“poor”,并具有各自的隶属度[7,19]。因此,当用广义可能性Kriple结构对动物的治疗过程进行建模时,广义标签函数可以用一个3维向量表示:
其中每一个数值表示一些药物的症状属性指标“高”“中”和“低”(当然,对于某些特定的药物,其他症状属性指标也可能存在,如“阴性”“零”和“阳性”)在状态" 上的可能测度。
同样,要说动物在药物治疗后(即:事件)究竟在什么时候从一种状态改变到另一种状态也是不精确的,因为每一次药物事件都可能导致从一个状态以不同的隶属度向多个状态转移[7]。因此,在使用广义可能性Kriple结构进行治疗过程建模时,可以将迁移分布(对应一个模糊事件)表示为3×3矩阵:
接着,我们只给出迁移分布" 和" 的建模过程(分别对应药物茶碱、异丙托溴铵),其他类似。考虑药物事件茶碱 。为简单起见,分别用符号h、m和l来表示原子命题“高”“中”和“低”。根据GFScom,可以看到,原子命题l和m分别是h的对立否定和中介否定,即l = h¬,m = h~。假设原子命题h对模糊事件 的“poor”“fair”和“good”3种状态的可能性分布为以下向量:
根据上述建模过程,我们采用有限数值化映射f为f (poor) = 1,f (fair) = 2且f (good) = 3。根据GFScom的定义,不难计算出其他原子命题l = h¬ = (0.1,0.3,0.8),m = h~ = (0.2,0.7,0.2)。假设初始广义标签函数是h = (0.8,0.3,0.1),根据医学理论和医生经验,对药物事件" 进行如下评估:
其中" 表示最大—最小运算。由模糊关系方程的解[20],我们可以通过求解上述方程得到无穷多个解,其中最大解如下:
其中" 表示Gödel蕴涵,即:
根据医学理论和医生的经验,取" 为:
对于药物事件 ,假设原子命题h(可能对应于另一个症状属性指数)在“poor”“fair”和“good”状态上的可能性分布为以下向量:h = (0.2,0.3,0.6)。类似地,我们可以计算其他原子命题为l = h¬ = (0.6,0.3,0.2),m = h~ = (0.4,0.7,0.4),并根据医学理论和医生的经验来评价药物" 如下:。与上面的计算过程类似,可以得到无穷多个解,其中最大的解如下:
根据医学理论和医生的经验,可以取" 为:
接下来,可以使用上述方法计算其他子迁移分布,具体如下:
4" 结" 论
本文的主要贡献如下:为了给广义可能性Kriple结构中的模糊事件提供一种便捷高效的建模方法,引入具有3种不同否定形式的广义模糊集GFScom,提出了基于GFScom的GPKS中事件建模方法。实例表明,该建模方法是有效的和简便的。
参考文献:
[1] ZADEHL A. Fuzzysets as a Basis for a Theory of Possibility [J].FuzzySets and Systems,1978,1(1):3-28.
[2] DUBOIS D,PRADE H. Possibility Theory and its Applications: Where Do We Stand [M]//KACPRZYK J,PEDRYCZ W. Springer Handbook of Computational Intelligence,Springer,2015:31-60.
[3] BAIER C,KATOEN J P. Principles of Model Checking [M].Cambridge:The MIT Press,2008.
[4] LI Y M,LI L J. Model Checking of Linear-Time Properties Based on Possibility Measure [J].IEEE Transactions on Fuzzy Systems,2013,21(5):842-854.
[5] LI Y M,MA Z Y. Quantitative Computation Tree Logic Model Checking Based on Generalized Possibility Measures [J].IEEE Transactions on Fuzzy Systems,2015,23(6):2034-2047.
[6] LI Y M. Quantitative Model Checking of Linear-Time Properties Based on Generalized Possibility Measures [J].Fuzzy Sets and Systems,2017,320:17-39.
[7] LUO M N,LI Y M,SUN F C,et al. A New Algorithm for Testing Diagnosability of Fuzzy Discrete Event Systems [J].Information Sciences,2012,187:224-232.
[8] HEERE H,JASPARS J,WANGR G. Partial Logic with Two Kinds of Negations as a Foundation for Knowledge-Based Reasoning [M]//Gabbay D M,WANSING H. What Is Negation. Oxford:Oxford University Press,1999:121-159.
[9] ANALYTI A,ANTONIOU G,DAMASIO C,et al. Negationand Negative Information in the W3C Resource Description Framework [J].Annals of Mathematics,Computing amp; Teleinformatics (AMCT),2004,1(2):25-34.
[10] KANEIWA K. Description Logic with Contraries, Contradictories, and Subcontraries [J].New Generation Computing,2007,25(4):443-468.
[11] FERRÉ S. Negation,Opposition,and Possibility in Logical Concept Analysis [C]//4th International Conference,ICFCA 2006.Heidelberg:Springer Verlag,2006:130-145.
[12] PAN Z H,ZHANG S L. Five Kinds of Contradictory Relations and Opposite Relations in Inconsistent Knowledge [C]//Fourth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD 2007).Haikou:IEEE,2007:761-764.
[13] PAN Z H,YANG L,XU J. Fuzzy Set With Three Kinds of Negations in Fuzzy Knowledge Processing [C]//AICI11: Proceedings of the Third International conference on Artificial Intelligence and Computational Intelligence.Qingdao:Springer-Verlag,2010:2730-2735.
[14] 潘正华.模糊知识的三种否定及其集合基础 [J].计算机学报,2012,35(7):1421-1428.
[15] 张胜礼,李永明.否定知识的代数表示及在模糊系统设计中的应用 [J].计算机学报,2016,39(12):2527-2546.
[16] ZHANG S L,LI Y M. A Novel Table Look-Up Scheme Based on GFScom and its Application [J].Soft Computing,2017,21(22):6767-6781.
[17] ZHANG S L,CHEN J. Modelling of Fuzzy Discrete Event Systems Based on A Generalized Linguistic Variable and Their Generalized Possibilistic Kriple Structure Representation [C]//Proceedings of the ICNC-FSKD 2022.Fuzhou:Springer,2023:437-446.
[18] CASSANDRAS C G,LAFORTUNE S. Introduction to Discrete Event Systems [M].Boston:Kluwer,1999.
[19] LIN F,YING H. Modeling and Control of Fuzzy Discrete Event Systems [J].IEEE Transactions on Systems, Man, and Cybernetics, Part B(Cybernetics),2002,32(4):408-415.
[20] 李永明.模糊系统分析 [M].北京:科学出版社,2005.
作者简介:张胜礼(1982—),男,汉族,江苏徐州人,教授,CCF高级会员(21359S),博士,研究方向:模糊系统、模糊逻辑、现代教育技术定量分析决策;陈静(1982—),女,汉族,江苏徐州人,讲师,硕士,研究方向:定量分析决策;吴娇(1998—),女,汉族,贵州毕节人,硕士研究生在读,研究方向:基础教育、教育信息技术。

