

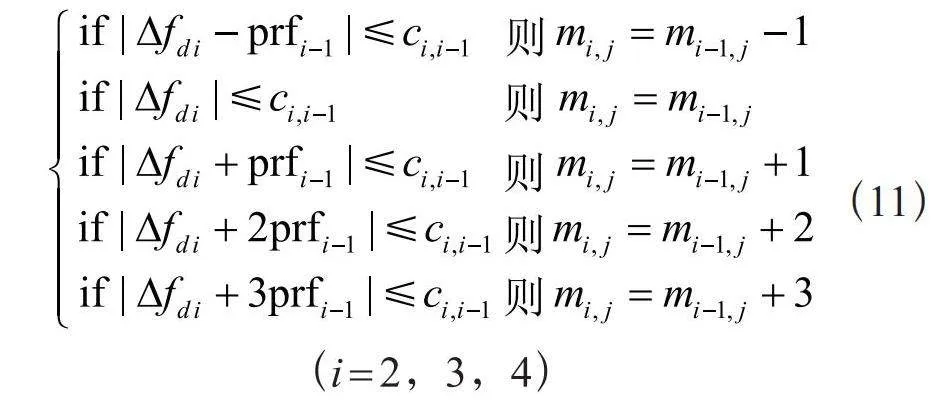
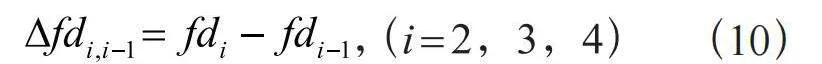





摘" 要:解速度模糊是脉冲多普勒雷达中需要解决的重要问题,通常的解速度模糊算法皆未考虑加速度信息,当雷达跟踪火箭弹等长助推段目标时存在速度解算误差大或无法解算、不能有效预测目标速度信息等问题。针对上述情况,提出一种面向加速度目标的解速度模糊算法。计算机仿真及雷达模拟数据表明,该方法对长助推段目标速度、加速度解算准确度高,对传统目标兼容性良好。该文还给出了新算法的工程实现方法。
关键词:脉冲多普勒雷达;解速度模糊;速度;加速度;
中图分类号:TP312" 文献标识码:A" 文章编号:2096-4706(2024)12-0061-05
A New Velocity Ambiguity Resolution Algorithm for Maneuvering Targets
WANG Jianqiang, HUANG Jinjie
(Xian Electronic Engineering Research Institute, Xian" 710100, China)
Abstract: Velocity ambiguity resolution is an important problem need to be resolved in pulse doppler radar. The usual velocity ambiguity resolution algorithms all do not consider acceleration information, and there are problems such as large velocity calculation errors or inability to solve, and inability to effectively predict target velocity information when radar tracks rocket shell and other long boost target. Aiming at the above situation, a velocity ambiguity resolution algorithm for acceleration targets is proposed. Computer simulation and radar simulation data show that this method has high accuracy in long boost target velocity, acceleration calculation, and good compatibility with traditional targets. The paper also provides an engineering implementation method for the new algorithm.
Keywords: pulse doppler radar; velocity ambiguity resolution; velocity; acceleration
0 引" 言
在脉冲多普勒(PD)雷达中常常会遇到解速度模糊和距离模糊的问题。为避免模糊并消除由距离遮挡、频率遮挡产生的目标丢失现象,一般采用多重PRF设计[1-3]。解模糊技术是PD雷达的关键技术,能否设计合理可行的多重PRF是保证目标检测概率和降低虚警率的关键[4]。对于解速度模糊,目前经常使用的解模糊算法有一维集算法和余差查表法。由于上述方法均未考虑加速度信息,当雷达跟踪长助推段目标时存在速度解算误差大或无法解算、不能有效预测目标速度信息等问题,本文提出一种针对带加速度目标的解速度模糊算法,结合对目标加速度的估计,实现对长助推段目标速度的有效预测,该方法已利用计算机仿真和雷达模拟数据进行了验证。
1" 解速度模糊基本原理
假设有4种重复频率进行速度测量,分别是prfi (i = 1,2,3,4),对应的滤波器宽度分别为∆Fi (i = 1,2,3,4),目标对应的滤波器号分别为Ni (i = 1,2,3,4)。则目标真实的多普勒频率为fd:
(1)
其中,mi (i = 1,2,3,4)为目标点所对应的各重复周期的模糊度。由于雷达稳定工作时,prfi、Ni、∆Fi均为已知参数,所以由模糊多普勒频率求解目标真实多普勒频率的过程本质是解同余方程组,解模糊的过程就是确定模糊度的过程[5]。
2" 常用工程实现方法比较及存在问题
余差查表法主要优点是在测速范围不大时,能够由模糊频率之差通过查表快速匹配出目标的真实多普勒频率,但随着目标的多普勒范围增大,对存储空间需求成倍增加[6],且浪费大量时间在不必要的频率值上。一维集算法可以准确地求得目标的真实多普勒频率值,且有一定纠错能力,缺点是计算量大[7-9]。最重要的是,以上两种常用方法在求解过程中皆未考虑目标加速度信息。当雷达跟踪长助推段目标时,其加速度特征将造成利用传统算法解算时速度误差过大、甚至无法解算的情况,导致雷达无法对长助推段目标进行跟踪。新算法的提出即为了解决以上问题。
3" 针对长助推段目标解速度模糊算法
3.1" 目标加速度对多普勒频率的影响
根据:
(2)
(3)
可得:
(4)
雷达从搜索发现目标至结束对该目标确认花费时间很短,可将具有加速度的目标在此时间段内看作均加速度运动,加速度设定为α。
prfi (i = 1,2,3,4)、mi (i = 1,2,3,4)、∆Fi (i = 1,2,3,4)、Ni (i = 1,2,3,4)的意义不再赘述,prfi按照从大到小排列,即prf1>prf2>prf3>prf4,对应重频的时刻记为ti (i = 1,2,3,4),对于prfi (i = 1,2,3,4)的可能模糊度依次为m1,m2,m3,m4。
(5)
(6)
由此得:
(7)
依式(7)可得:
(8)
加速度可表示为:
(9)
在上式中,除了重频prfi、prfi-1的模糊度mi、mi-1未知外,其他皆已知。
3.2" 基于最小二乘的解速度、加速度算法
按照雷达跟踪目标最大速度,结合已经选定的prf,可估计模糊度解集的最大模糊度值M,采用遍历的方法,以c = 2∆F1作为不考虑目标加速度修正时模糊度解集是否存在的基础判定常数。若不同prf对应的某假定模糊度计算出的目标多普勒频率之差符合不等式判定条件,则该模糊度为潜在模糊度解,纳入可能的模糊度解集Mj。结合式(5)(6),得到:
(10)
以下,对fd为正的情况进行分析,fd为负时情况类似。当雷达观测目标具有加速度特征时,不同重复频率、波束功能下目标多普勒变化是不同的,每个∆fdi, i-1不等式的判定准则需要按照雷达实际工作流程,对基础判定常数c进行修正。以表1举例说明。
结合表1,将m1从0,1,2,…,M进行遍历:
(11)
否则无解[10]。
若对于i = 2,3,4均有解,表示用于遍历的该模糊度对应的m1、m2、m3、m4为可能的一组模糊度解。这里,将prf1对应的所有可能模糊度解记为集合j,将不同重复频率所有可能模糊度组解记为解集Mj = { j,m2 j,m3 j,m4 j}。
对于解集Mj,结合式(9),可获得每组解集对应的存在加速度α,将解集重新记为" ={ j,m2 j,m3 j,m4 j,αj}。这时,针对可能模糊度解集 ,将每组解包含的加速度信息进行修正:
(12)
(13)
至此,重新获得了不包含加速度信息的多普勒频率方程组,对所有可能存在的模糊度解集,如下所示求解ε:
(14)
(15)
找出ε中最小的一个,其对应的一组模糊度解即为目标的模糊度计算结果,对应的" 即为搜索到目标时的多普勒频率。利用式(9)得:
(16)
求得的平均加速度即为从搜索发现目标至结束对该目标确认时间段内的平均加速度。
4" 新算法的计算机仿真与分析
结合实际应用条件,仿真参数如下设置:
目标最大速度范围10~1 000 m/s,目标最大加速度范围-10~500 m/s2,重复频率prfi (i = 1,2,3,4)分别为4.87、4.47、4.10、3.79 kHz,对应的重复周期分别为205、223、243、26 3μs,32点积累,波驻分别为6.5、7.14、7.78、8.42 ms,滤波器宽度分别为152、140、128、118 Hz,波长为0.033 m。下文进行仿真分析。
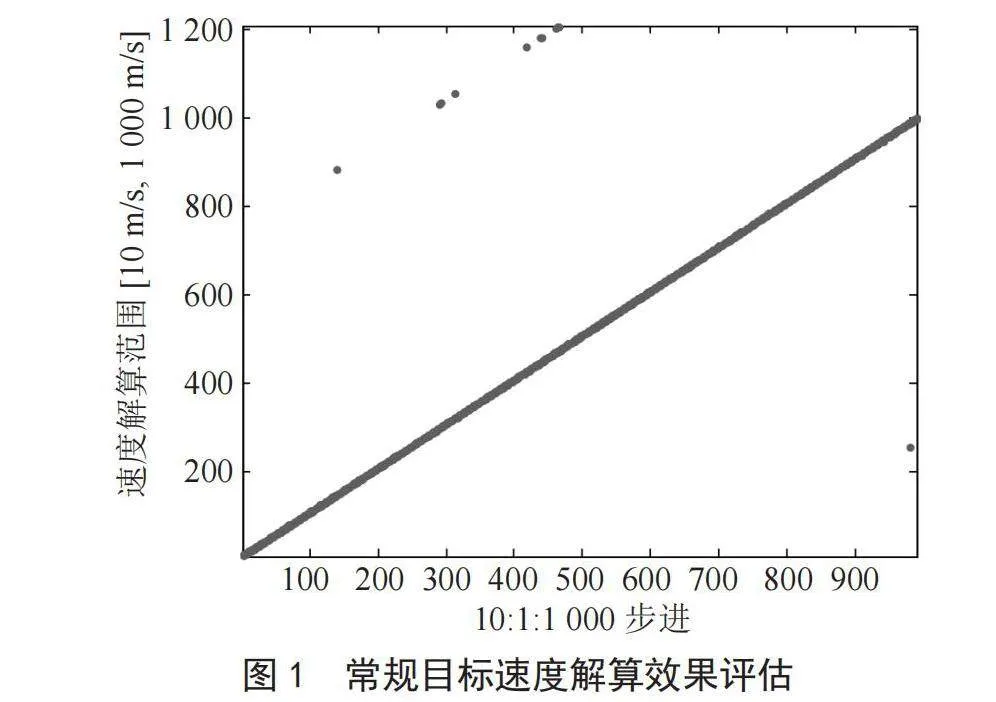
4.1" 解常规目标速度模糊效果评估
为了验证新算法普适性,首先利用新算法评估解算常规目标的效果:取速度范围10~1 000 m/s,加速度范围-10~10 m/s2,若雷达工作时重复频率按照prf1、prf2、prf3、prf4顺序排列,不等式判定常数为基础常数[-c,c]。仿真结果如图1所示,速度解算误差以 ∆ ≤3.0 m/s统计,ε最小解正确率为98.89%。
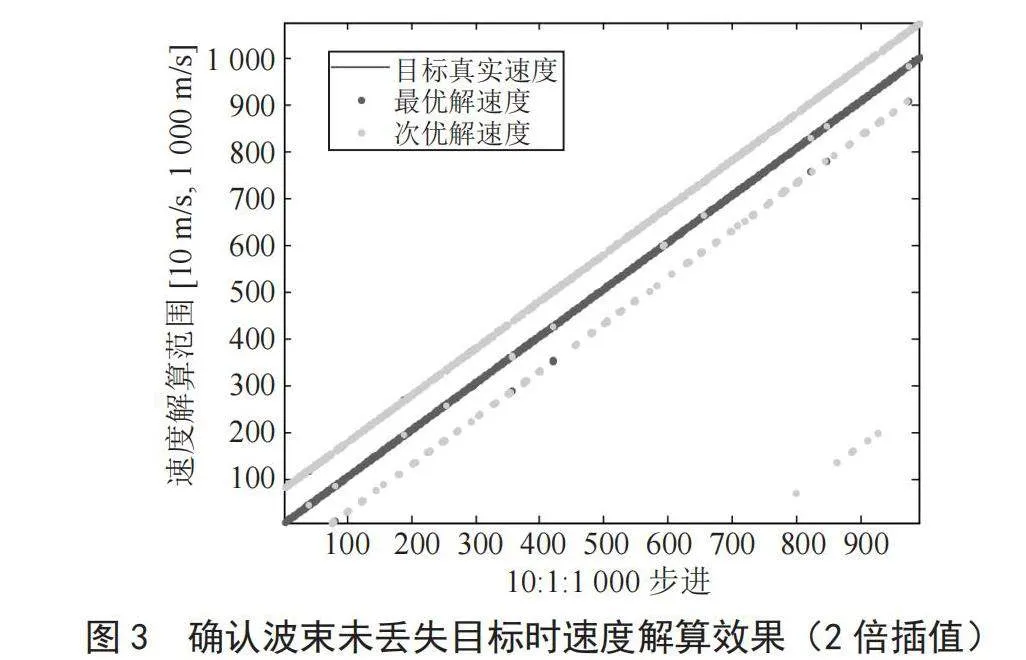
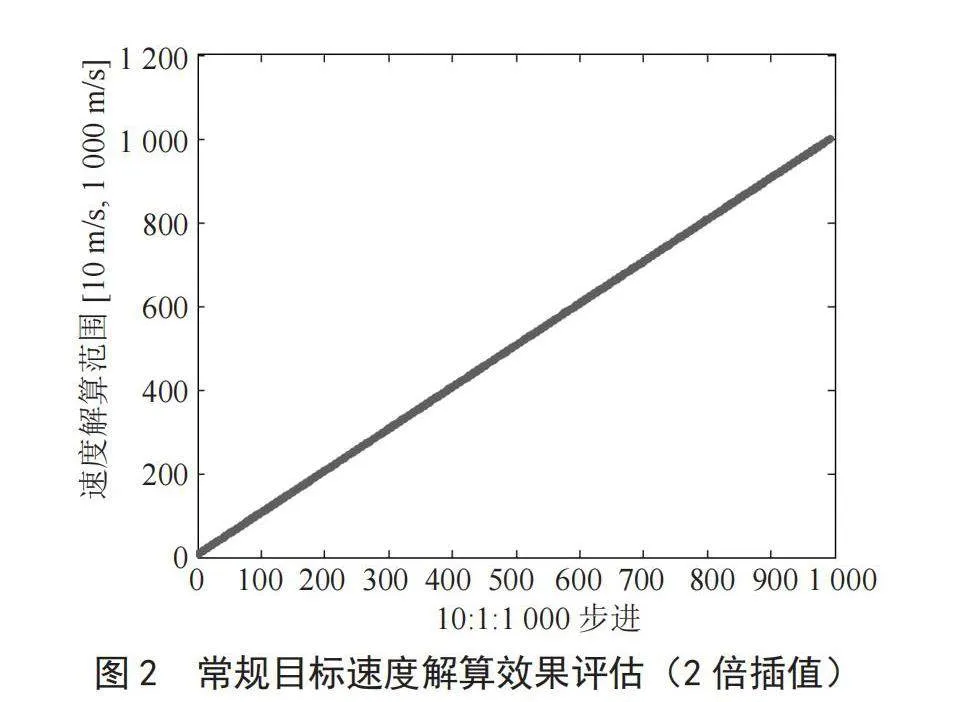
分析仿真数据可知,对常规目标速度解算未能达到100%概率的主要原因是剩余1.11%的正解为ε次小解,这主要受多普勒滤波器宽度影响。实际工程应用中,信号处理器通过多普勒滤波器插值,适当提高MTD滤波器精度,即可解决该问题。仿真结果如图2所示,MTD滤波器2倍插值后,速度解算误差以 ∆ ≤1.5 m/s统计,ε最小解正确率100%,可见滤波器插值后既提高了ε最小解是正解的概率,也提高了速度解算精度。
4.2" 解长助推段目标速度模糊效果评估
接下来评估新算法对长助推段目标的解算效果。结合长助推段目标弹道数据,取速度范围10~1 000 m/s,加速度范围-10~500 m/s2。
4.2.1" 确认波束未丢目标时
若雷达工作时重复频率按照prf1、prf2、prf3、prf4顺序排列,结合雷达搜索、确认波束时间关系及加速度范围,对不等式判定准则做如表2所示的修正。
多普勒滤波器2倍插值时,仿真结果如图3所示,速度解算误差以 ∆ ≤1.5 m/s统计,ε最小解正确率98.18%,ε次小解正确率1.82%。滤波器插值后,受目标加速度对不等式判定范围的影响,ε最小解正确率未达到100%。
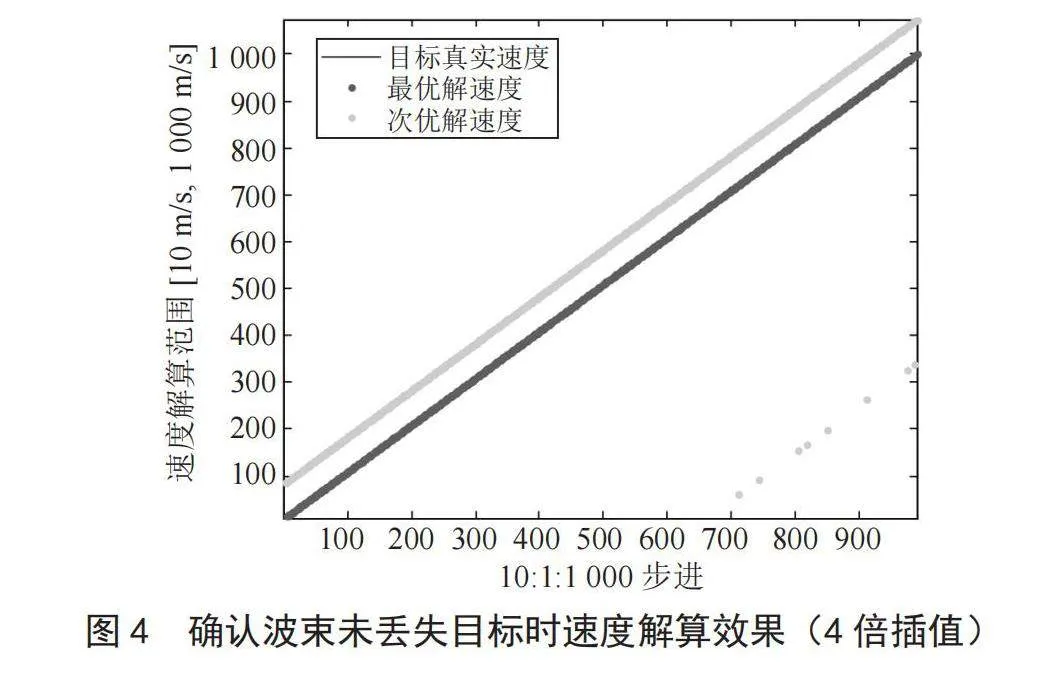
多普勒滤波器作4倍插值时,仿真结果如图4所示,速度解算误差以 ∆ ≤1.0 m/s统计,ε最小解正确率100%。可见,随着多普勒滤波器分辨率不断提高,长助推段目标速度解算的正确率在更高的精度得到了保证。
一般地,雷达搜索重频参差发射,工作时序关系的变化使得长助推段目标的加速度对不等式解算范围的影响也略微发生变化。实际工程应用时,可按照雷达不同波束功能间实时的时序关系,对表2中的不等式判定范围作出适当调整。
4.2.2" 确认波束丢失一次目标时
雷达实际工作时,受目标起伏、目标频率遮挡和动杂波等因素影响,往往不能保证每个确认波束都能确认到目标。根据m/n原则,当确认波束丢失一次目标时,仍然认为对目标完成了有效确认,下面对此类情况作具体分析,评估确认丢失一次目标时的速度解算效果。
类似的,若雷达工作时重复频率按照prf1、prf2、prf3、prf4顺序排列,假设prf3丢失目标,结合雷达搜索、确认波束时间关系及加速度范围,对不等式判定准则做如表3所示的修正。
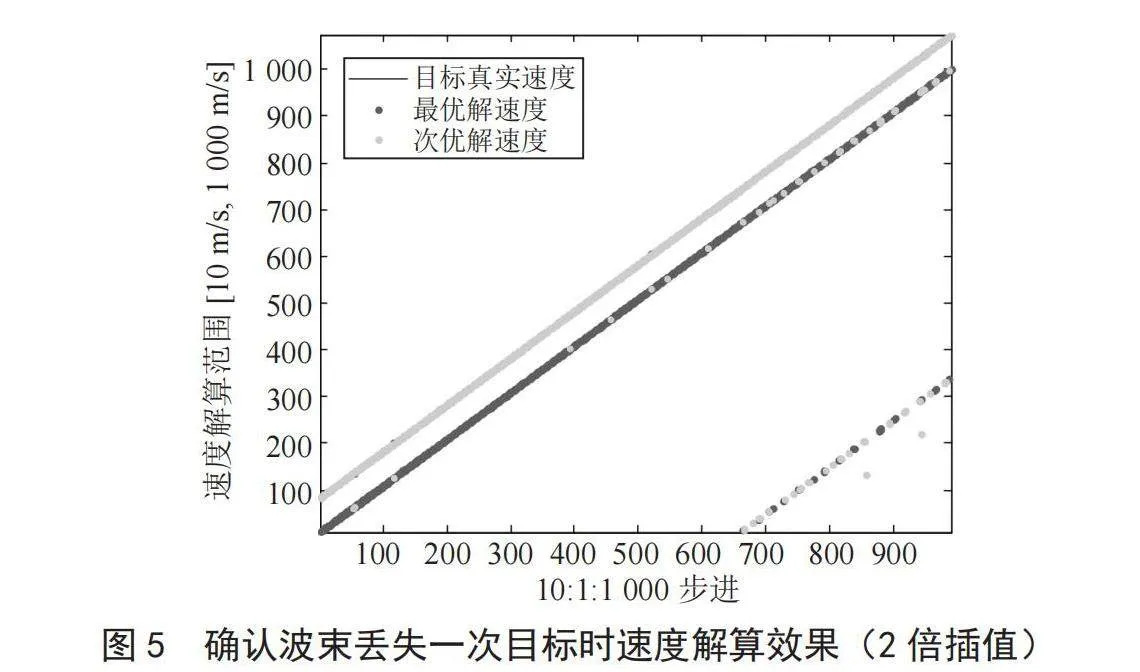
多普勒滤波器2倍插值时,仿真结果如图5所示,速度解算误差以 ∆ ≤1.5 m/s统计,ε最小解正确率95.96%,ε次小解正确率4.04%。对比4.2.1节确认波束未丢失目标的情况,可以看出ε最小解正确率出现2.22%下降,因为该部分的目标速度正解成为ε次小解,这是由确认波束丢失一次目标后参与速度解算的不等式判定准则发生变化造成的。
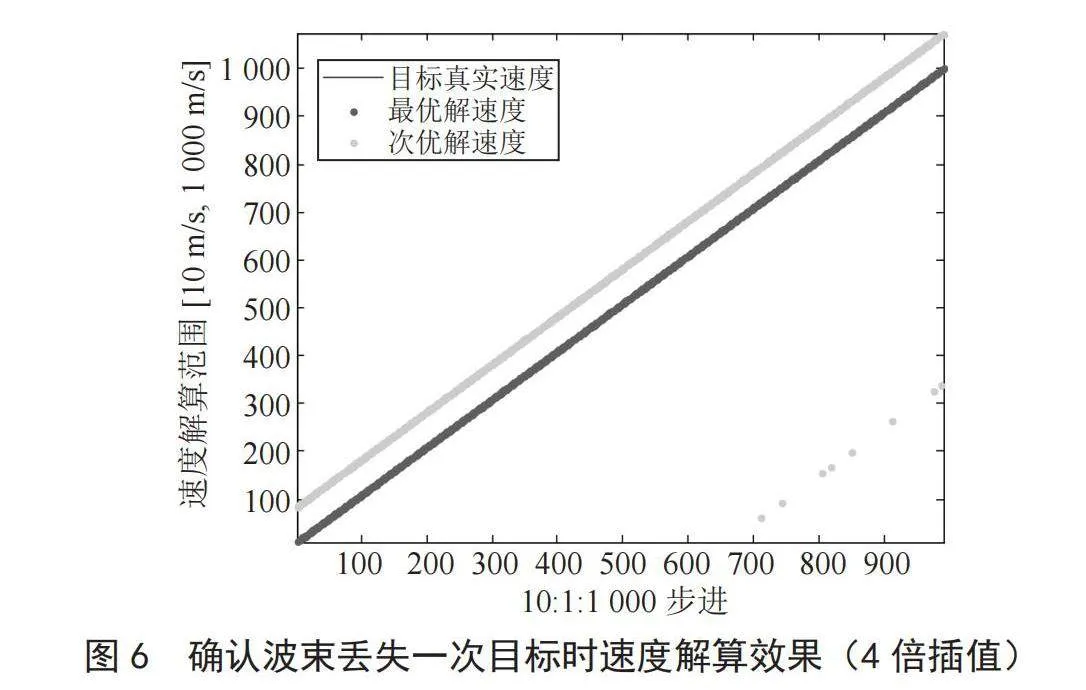
同样的,多普勒滤波器作4倍插值时,仿真结果如图6所示,速度解算误差以 ∆ ≤1.0 m/s统计,ε最小解正确率100%。可见,即使在确认波束丢失一次目标时,多普勒滤波器分辨率的提高依然在更高的精度上保证了长助推段目标速度解算的正确率。
4.3" 解长助推段目标加速度效果评估
下面,分别按照4.2.1、4.2.2节的仿真参数设置,对解长助推段目标加速度的情况展开讨论。由于某一固定目标速度、加速度时,速度的ε最小解、次小解和加速度的ε最小解、次小解完全一一对应,故加速度解算正确率可参考4.2节讨论,以下只统计加速度解算误差。
4.3.1" 确认波束未丢目标时
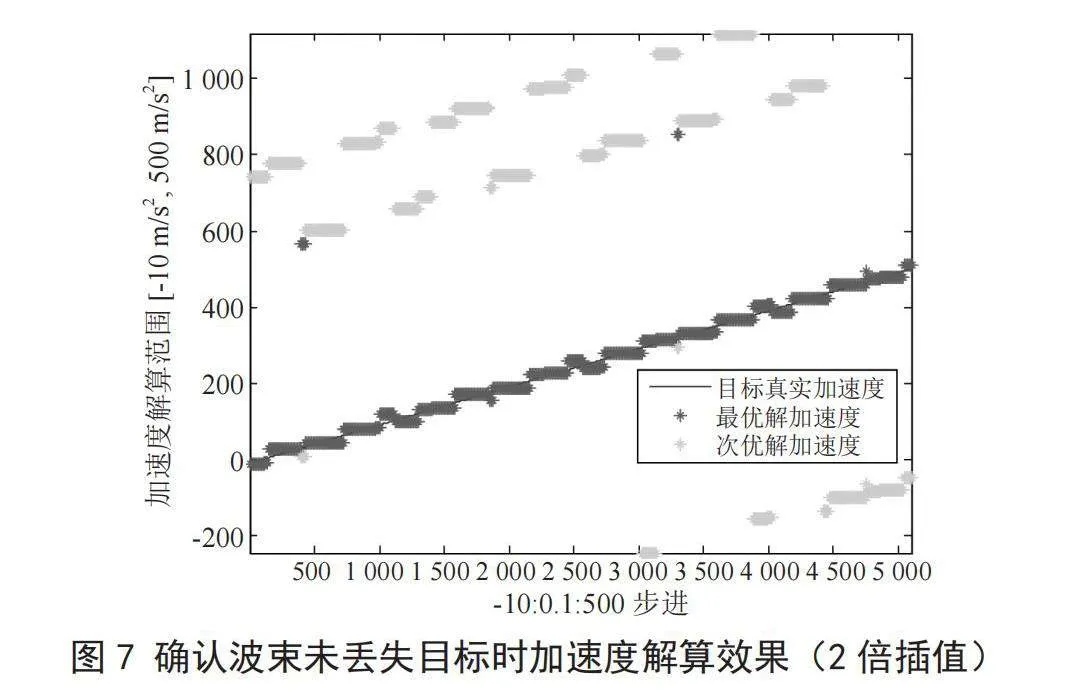
仿真参数详见4.2.1节,多普勒滤波器2倍插值时,仿真结果如图7所示。加速度解算误差 ∆ ≤25 m/s2。
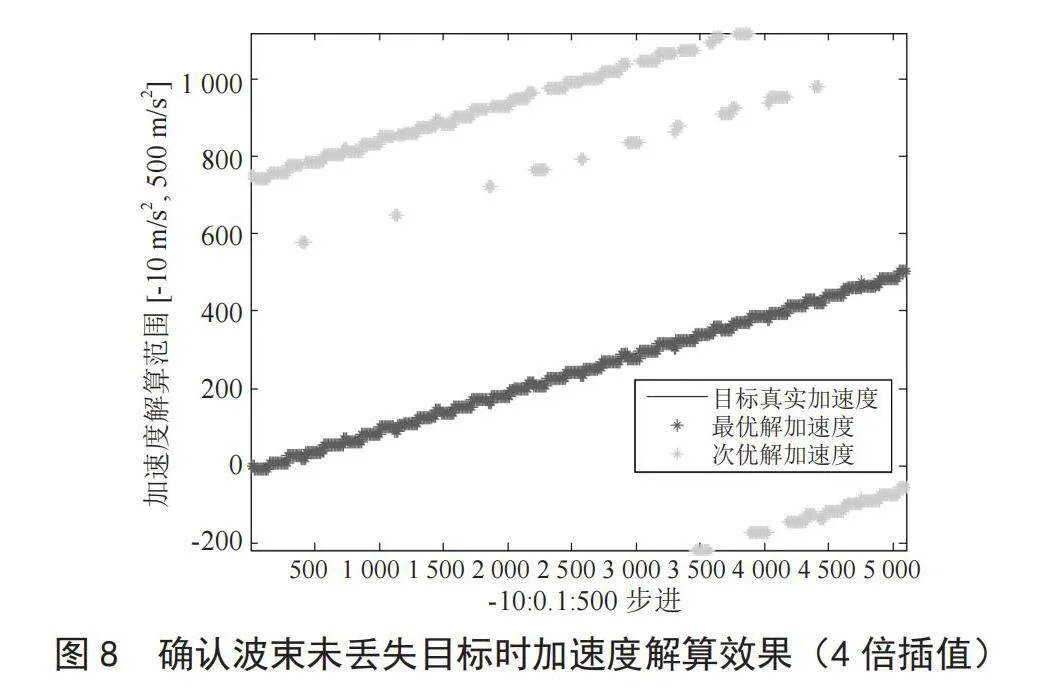
多普勒滤波器4倍插值时,仿真结果如图8所示。加速度解算误差 ∆ ≤17 m/s2。
4.3.2" 确认波束丢失一次目标时
由于多普勒滤波器2倍与4倍插值时,加速度解算误差与4.3.1节基本相同,这里不再重复讨论。
4.4" 仿真结果及工程实现中注意事项
根据4.1至4.3节内容可知,多普勒滤波器2倍插值后,新算法对常规目标和长助推段目标速度维解算概率和误差已能满足雷达系统工作要求;对长助推段目标的加速度解算误差也在合理范围内,满足雷达对长助推段目标跟踪时的多普勒波门预测要求。需要注意的是,2倍插值时常规目标的ε最小解全部为正解,但长助推段目标由于受加速度影响,很小一部分速度正解却落在了ε次小解。工程上为保证对各类目标速度均有100%的解算概率,应同时保留ε最小解和次小解,在后续跟踪时予以剔除。多普勒滤波器4倍插值时,则不存在上述问题。
工程实现时,受系统硬件水平制约,暂时使用曲线拟合的方法对多普勒滤波器进行插值。该方法受信噪比及参与曲线拟合通道的幅度起伏限制,可稳定保证2倍插值精度,但无法100%达到4倍插值精度的设计要求。后续硬件水平允许的情况下,利用FIR滤波器设计灵活的特点,结合DSP对目标所在重点多普勒区域做二次检测,可稳定保证多普勒维4倍插值精度,完全避免速度正解落入ε次小解的情况。
目前,该算法已在某雷达系统中利用弹道模拟数据及动态跟飞试验中得到了进一步的验证。
5" 结" 论
通常的解速度模糊算法均未考虑目标加速度信息,跟踪火箭弹等带加速度目标时往往出现速度解算误差大或无法解算、不能有效预测目标速度信息等问题。本文提出了一种针对带加速度目标的解速度模糊算法,通过理论分析和计算机仿真,详细评估了新算法解算常规目标和长助推段目标的实际效果,并给出了工程实现方法及注意事项。仿真结果表明,该算法对常规目标兼容性良好,对长助推段目标的速度、加速度解算精确,具有工程应用价值。
参考文献:
[1] 丁鹭飞,耿富录,陈建春.雷达原理 [M].北京:电子工业出版社,2013.
[2] 王德纯,丁家会,程望东.精密跟踪测量雷达技术 [M].北京:电子工业出版社,2006.
[3] 陈伯孝.现代雷达系统分析与设计 [M].西安:西安电子科技大学出版社,2012.
[4] 张代忠,洪一,邱炜.脉冲多普勒雷达中的解模糊算法及实现 [J].雷达科学与技术,2004(5):293-297+314.
[5] TRUNK G,BROCKETT S. Range and Velocity Ambiguity Resolution [C]//The Record of the 1993 IEEE National Radar Conference.Lynnfield:IEEE,1993:146-149.
[6] 刘志英.基于剩余定理和一维集法的PD雷达解模糊处理 [J].现代电子技术,2012,35(9):28-30.
[7] 雷文,龙腾,曾涛,等.一种脉冲多普勒雷达解距离模糊的新算法 [J].北京理工大学学报,1999(3):357-360.
[8] 谢锋,齐润东.单目标解模糊 [J].系统工程与电子技术,1998(6):34-38.
[9] 何劲.脉冲多普勒雷达速度模糊的求解 [J].电讯技术,1999(4):18-23.
[10] 冯克勤,余红兵.初等数论 [M].北京:中国科学技术大学出版社,1995.
作者简介:王建强(1984.06—),男,汉族,甘肃平凉人,雷达总体线路设计师,高级工程师,硕士研究生,研究方向:雷达总体设计。


