









摘" 要:低峰均比序列是第五代移动通信技术中常用的一种随机序列,在多个上行信道中作为导频信号使用。根据不同的应用场景,低峰均比序列定义了不同的生成公式。文章研究了序列的定义,并结合工程实践,分析了传统查找表法应用于单位圆序列带来的精度问题和存储问题。通过研究CORDIC原理,文章提出了一种基于CORDIC的低峰均比序列生成算法,并与查表法进行了对比分析。该方法在序列数据位宽固定时,通过增加迭代次数,能够达到最大数据精度并且不占用存储空间。
关键词:5G NR;低峰均比序列;CORDIC算法;查找表法
中图分类号:TN929.5" 文献标识码:A" 文章编号:2096-4706(2025)03-0015-05
A 5G NR Low PAPR Sequence Generation Algorithm Based on CORDIC
WANG Han, WANG Linan
(The 54th Research Institute of CETC, Shijiazhuang" 050081, China)
Abstract: The low Peak to Average Power Ratio (PAPR) sequence is a random sequence commonly used in the fifth generation mobile communication technology, which is used as a pilot signal in multiple uplink channels. According to different application scenarios, different generation formulas are defined for the low PAPR sequence. This paper studies the definition of sequence, and combines with engineering practice to analyze the accuracy and storage problems caused by the traditional look-up table method applied to unit circle sequences. By studying the principle of CORDIC, this paper proposes the low PAPR sequence generation algorithm based on CORDIC, and carries out comparative analysis with the look-up table method. This method can achieve maximum data accuracy and does not occupy storage space by increasing the number of iterations when the sequence data bit width is fixed.
Keywords: 5G NR; low PAPR sequence; CORDIC algorithm; look-up table method
0" 引" 言
2018年6月14日,第三代合作伙伴计划(3rd Generation Partnership Project, 3GPP)全体会议正式批准了第五代移动通信技术的独立组网标准[1]。第五代移动通信新空口技术(5G New Radio, 5G NR)定义了两类随机序列:伪随机序列和低峰均比序列。伪随机序列主要应用于下行信道和非基于码本传输的上行共享信道中;而低峰均比序列应用于基于码本传输的上行共享信道、四种格式的上行控制信道以及上行探测信号中[2]。顾名思义,低峰均比序列的峰值功率与平均功率比值较小,应用于发射端有利于提升发端的功放效率,在通信系统中有广泛的应用[3]。5G NR的低峰均比序列具有恒包络的特性,序列分布在单位圆上[4]。在工程应用中,分布在单位圆上的序列常使用查找表法计算,但该方法的精度受限于查找表的大小,精度提升以增大存储开销为代价。文章根据5G NR标准R15版本中低峰均比序列的定义,提出了一种基于CORDIC的序列生成算法,并在文章中对两种方法进行了对比分析,新算法可以在不占存储的情况下有效提升序列精度。
1" 低峰均比序列定义
低峰均比序列由式(1)定义:
(1)
在上述定义中,为基序列,是低峰均比序列的长度,为每个资源块包含的子载波个数,固定为12,α为循环移位,δ根据信道类型决定,同一个基序列通过不同的α和δ可以产生多个低峰均比序列[5]。当序列长度确定时,根据其他参数U、v的不同配置,基序列可以生成多个。因此,5G NR根据参数u,v将基序列进行了分组,为组号,v为组内的序列号。当v = 0时,1个组只包括1个基序列,每个基序列的长度是,其中,此时序列长度小于等于60个;当v = 0,1时,1个组包括2个基序列,,其中,此时序列长度大于60个。
基序列根据序列长度MZC有不同的定义公式。对于,基序列由式(2)定义,其中由5G NR标准中的4个表格定义,每张表格对应MZC的1种取值,每个表格中的元素,通过不同的u查询表格中序列的不同取值。
(2)
对于MZC = 30,基序列由式(3)定义:
(3)
当,基序列长度大于等于36时,基序列由式(4)定义:
(4)
其中:
(5)
长NZC为满足NZC<MZC的最大质数。
通过分析上述低峰均比序列的定义,可以得出序列生成式(1)主要分成循环移位和基序列两部分计算。根据5G NR标准定义,循环移位的α取值由信道类型决定:当低峰均比序列应用于基于码本的PUSCH信道时,α = 0;应用于PUCCH时,e jαn至多有12种取值;应用于SRS时,e jαn至多有16种取值。在工程实现中,e jαn可以通过查找表的方式产生,查找表的深度为38,宽度由数据精度决定。循环移位的计算简单,但基序列有三种定义公式,因此计算较复杂。通过分析基序列的定义可得,当时,基序列有4种取值,当MZC = 30时,基序列有62种取值,因此当长度小于36时,使用查找表的方式产生基序列简单易行。当时,根据5G NR标准规定,基序列长度MZC共有92种取值,最小为36,最大为1 632。为了方便分析,设的相位为,由式(6)表示:
(6)
由于NZC作为相位的分母,因此在2π周期内相位存在至多2NZC种准确取值。NZC与MZC一一对应,共有92种取值,因此在这种情况下,如果遍历所有NZC取值,将基序列做成查找表,存储量非常庞大。针对这种情况,如果在工程中采用查找表生成序列,常用的方法是以牺牲相位精度的代价来限制查找表的大小。比如,将第一象限的单位圆量化成2 048点的查找表,计算相位时将其量化成查找表中最接近的一个元素。但此时计算出的基序列精度与查找表的大小成正比,表格越大,相位精度越高,量化误差越小[6]。针对时,采用传统查找表产生的相位精度问题,文章采用CORDIC算法来规避,下一节介绍CORDIC算法基本原理。
2" CORDIC算法原理
在笛卡尔坐标系中将向量旋转θ角度到新向量,如式(7)所示:
(7)
等号右边提取出,设,,
可得新方程如式(8)所示:
(8)
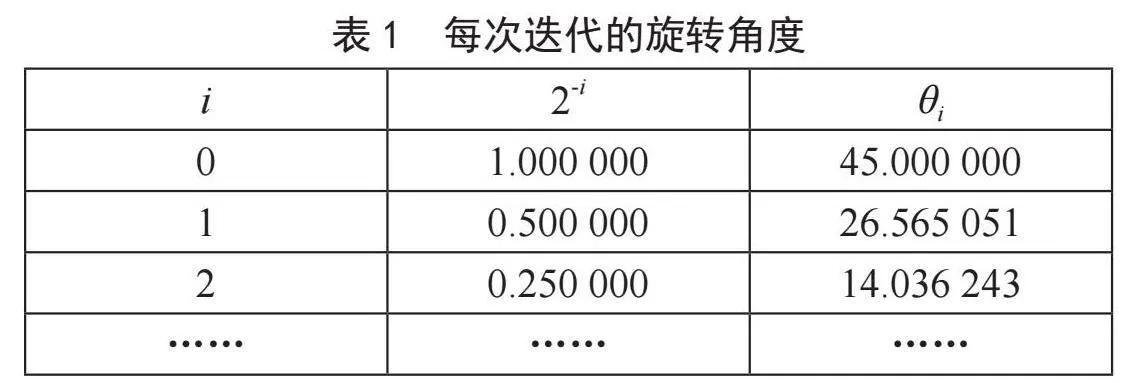
采用迭代的思想分析向量旋转过程,原始向量的一次旋转其实可以分解为多次旋转,旋转角度大小和方向均可不同。假设旋转迭代次数为i,每次旋转的角度为θi,则旋转总角度θ为多次旋转角度θi之和。为了方便分析计算,对旋转角度θi赋予一定规律性,设,则,可以得出如表1所列的旋转角度值[7]。θi为一个递减的收敛序列,序列的级数和为99.7度,因此对任意范围内的角度都可以通过多个小角度θi累加求和来计算[8]。对于该范围之外的角度,可以利用三角恒等式将其折算到此范围来应用。
在表1中,旋转角度θi全部为正值,考虑旋转的正负方向,引入旋转的方向指示变量di,当逆时针旋转时di = 1,当顺时针旋转时di = -1,每次旋转完毕新向量的角度设为zi,角度累加方程如式(9)所示:
(9)
将带入式(8),同时考虑旋转方向,可得出迭代过程中任意一次旋转计算如式(10)所示:
(10)
通过式(8)可得,相比每次旋转的起始向量,本次旋转后终点向量的模值增大为倍,因此在所有旋转完成后,需将新向量乘以系数 得到单位圆上的最终向量,如式(11)所示:
(11)
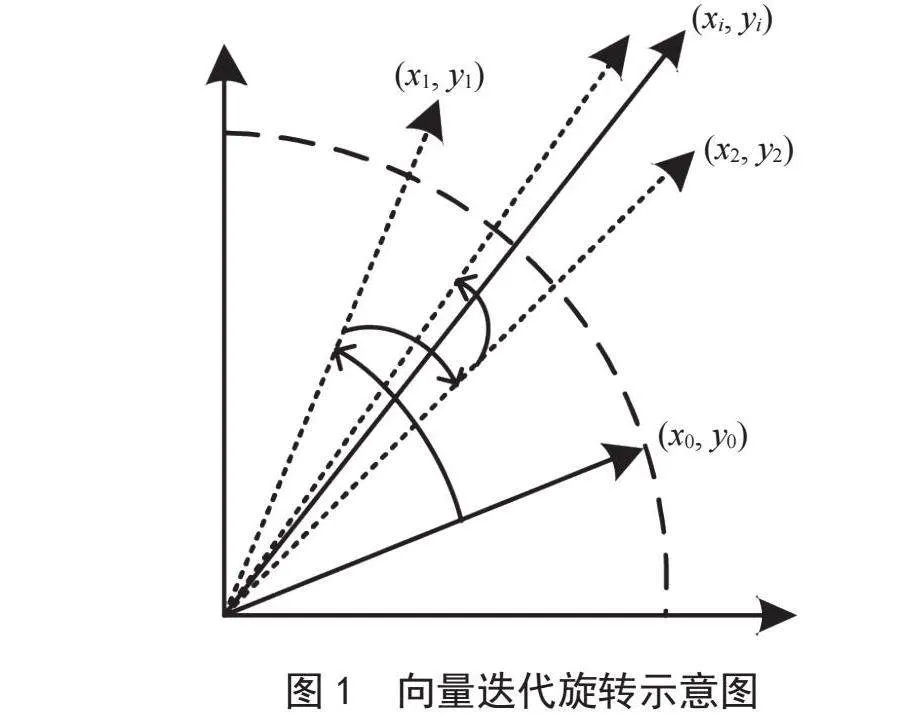
由式(8)~式(11)可得,CORDIC的基本原理是运用迭代的思想将向量一次旋转过程分解为多次小角度旋转来完成,并且在此过程中将三角函数运算转化为多次移位和加减运算,极大地减小了计算量[9]。向量的旋转示意图如图1所示。
3" 基于CORDIC算法的序列生成
将低峰均比序列的定义和CORDIC算法原理结合分析可得,使用CORDIC算法计算时,等效于令向量的初始值,将初始向量旋转相位得到目标向量的过程,因此的计算转化成相位的计算。考虑在工程实现中引入π会带来一定计算复杂度,对做化简,两边消去π可得:
设 = m(m+1)q/NZC,则式(12)将计算转化成以2为周期的计算。
0≤m(m+1)q/NZC<2 (12)
通过分析低峰均比序列在各上行信道中的应用,可以枚举出序列的长度MZC共有92种取值,最小为36,最大为1 632。NZC作为小于MZC的最大质数,无法实时计算只能存储成查找表。在计算的过程中,首先根据序列长度MZC查询出NZC,然后结合u,v计算出,最后通过序列索引m计算并进行模除操作。
由于式(12)对输入相位进行了化简,因此CORDIC内部每次迭代累加的小角度相位也需进行相同的化简处理,将θi转化成与相同的量纲。转化过程可以通过式(13)计算,的单位是弧度,将其转化成与相同的量纲时记为。
(13)
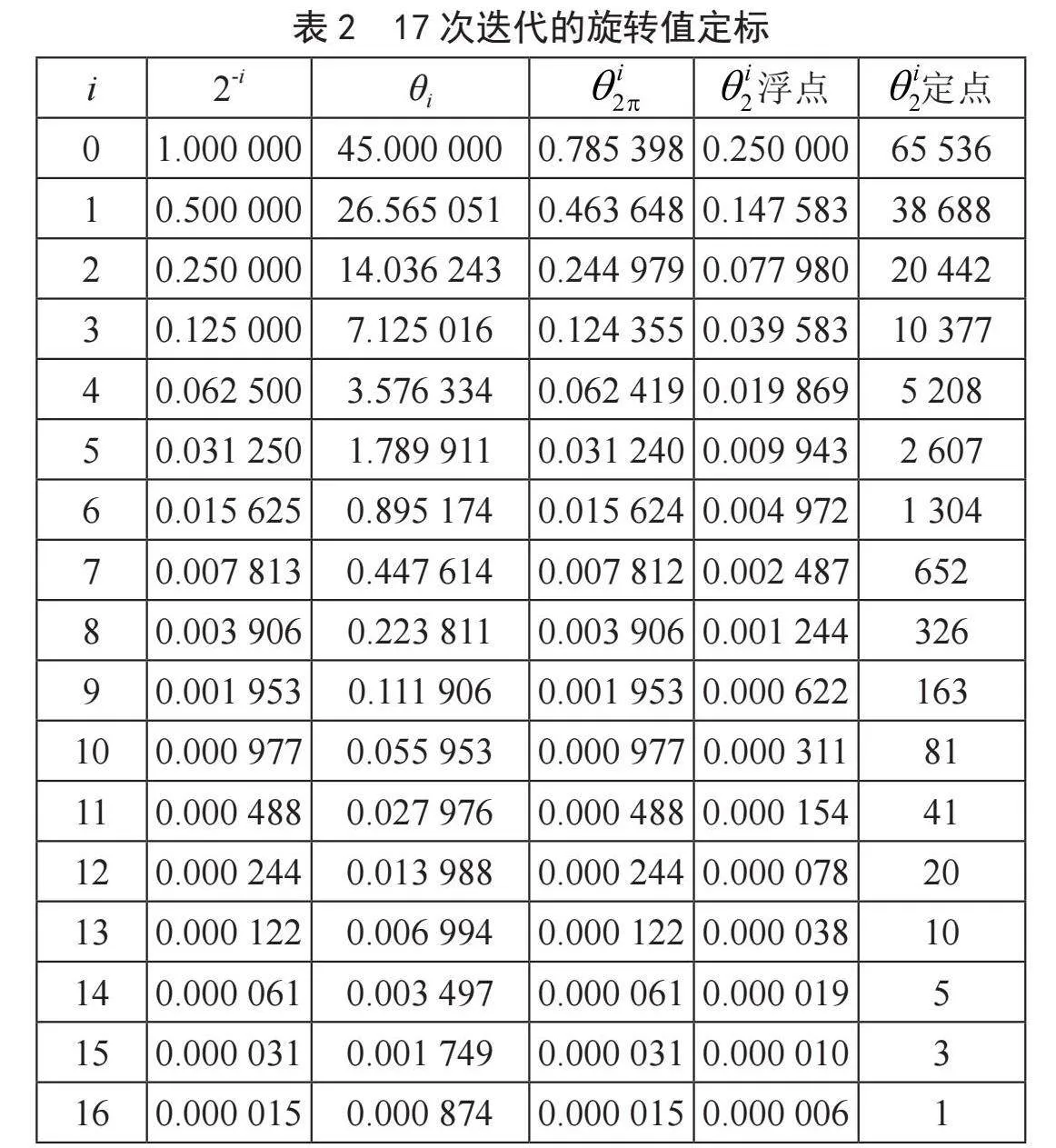
角度简化完毕,下一步是根据要求的数据精度确定迭代次数,进而对角度定标。由式(10)可得每次迭代过程都对向量的实部虚部进行一次移位操作,因此迭代次数比向量数据位宽大时即可满足最大的精度。在工程实现中,低峰均比序列的数据实部虚部均为16 bit位宽,由此推出CORDIC的迭代次数设置为17次。每次旋转作为累加的" 是一个小数,为了保证每次迭代时的有效性, 必须是一个非零值,因此当第17次迭代时, 的十进制小数位宽最小保留6位,转化成二进制时小数部分保留18位。由式(12)可得" 小于2,因此在工程定标时,将" 和" 的总位宽定标成19位,其中小数部分保留18位,整数部分保留1位, 的浮点和定点数据如表2所示。
上述角度简化和定标结果分析完毕,即可根据CORDIC计算序列长度时的低峰均比序列。对于另外两种情况,当序列长度时,根据式(1)~式(3)采用查找表的方式生成序列。结合FPGA工程实现,将基于CORDIC计算低峰均比序列的步骤表述如下:
1)初始向量定标。在工程实现中,生成的低峰均比序列用16 bit位宽表示,小数部分保留15 bit,因此将CORDIC算法旋转的初始向量实部表示成32 768,虚部为0。
2)根据参数计算初始相位。将质数NZC预先存储到ROM,根据序列长度MZC查表获得NZC,由输入参数u,v和式(5)计算q。对每一组输入参数MZC,u,v计算出唯一的q/NZC,将其小数部分量化成18 bit位宽,与的定标保持一致。序列的索引值m从0开始递增,依次计算出序列每个点对应的旋转初始相位z0。
3)迭代计算。考虑到FPGA实现的全流水需求,将每次迭代计算进行一次例化,每次例化的输入输出均为相位、实部和虚部。第一次迭代时,根据初始相位z0的符号位正负计算d0,根据式(9)、式(10)和表2中的计算第一次迭代的结果z1和,将其作为第二次迭代的输入和表2中的相位" 联合计算得到第二次迭代输出,累加迭代17次得到末次向量 。
4)归一化和循环移位。将末次向量的实部虚部乘以缩放因子归一化到单位圆,得到基序列 。根据循环移位α和序列索引查表得到e jαm,与基序列相乘得到最终的低峰均比序列。
新算法基于FPGA平台实现的迭代计算时序示意图如图2所示。
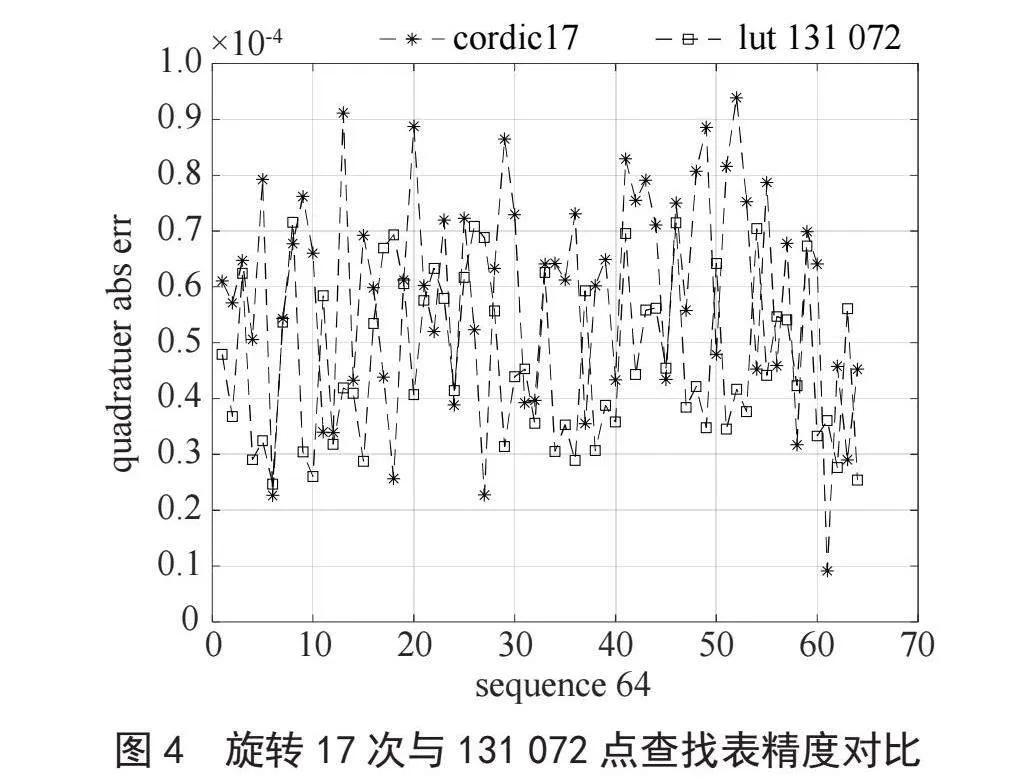
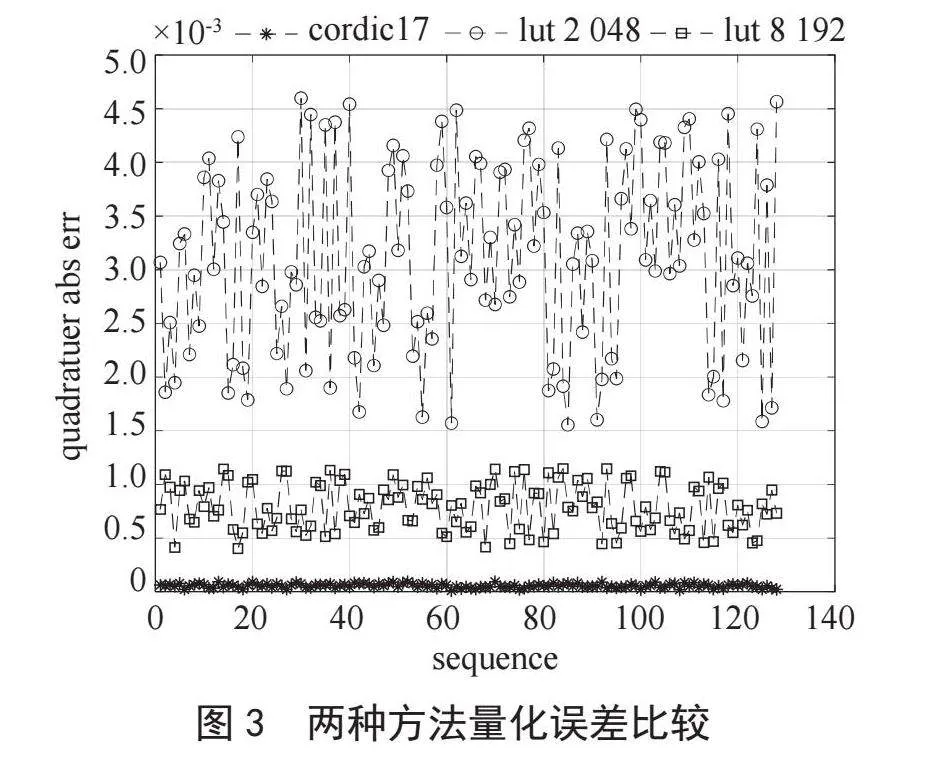
综上所述,采用基于CORDIC算法生成低峰均比序列有两种优势,一是不占用大量的存储资源;二是生成序列的精度可以通过配置迭代次数提升,当迭代次数比向量位宽大时,可以得到最大量化精度。当 时如果使用查找表的方法生成低峰均比序列,序列的精度与查找表的大小有关系。图3对比了使用两种方式生成序列时的量化误差[10],使用CORDIC算法计算时迭代次数设置为17次,使用查找表的方法生成序列时,将单位圆量化成2 048点和8 192点。在此场景下,基于CORDIC算法生成序列的精度明显优于查找表法。
由图3分析查找表方法的量化误差,当表格点数从2 048点提升到8 192点时,量化误差的均值也减小为原来的1/4,因此继续增大表格大小可以使查找表法的量化误差与CORDIC算法生成序列的量化误差达到同一量级。由式(11)可得,在旋转的过程中末次旋转向量会增大为初始向量的倍, 是一个递增的收敛序列,极限值小于2。因此,在工程实现中,假设低峰均比序列的实部虚部均为16 bit位宽,向量的模值在旋转过程中会增大,需用17 bit位宽表示。由式(10)可得,当旋转次数大于17时,等号右边和为0,继续增大旋转次数,向量的实部虚部不会变化,相应基序列精度也不会增加。与查找表算法对比分析,当查找表格的点数增大到217时,两者精度一致,如图4所示。为了仿真图分辨清晰,图4只画出了64点序列的量化误差。
4" 结" 论
得益于包络恒定、峰值功率波动小等优良特性,低峰均比序列在通信系统中具有重要的研究意义。文章首先分析了5G NR中低峰均比序列的定义,并基于其公式研究了在工程实现中采用查找表法计算序列时面临的问题。随后,结合CORDIC算法的基本原理,提出了一种新的低峰均比序列生成算法。结合工程实践,文章对新算法进行了定标并简述了计算步骤,对比分析了在某些场景下新算法和查找表法的量化误差,新算法在不产生存储开销的同时能有效提高序列精度,对工程实现具有一定的指导意义。
参考文献:
[1] 杨立.5G-NR蜂窝系统功能演进趋势分析 [J].无线电通信技术,2020,46(3):310-314.
[2] 张建国,杨东来,徐恩,等.5G NR物理层规划与设计 [M].北京.人民邮电出版社,2020:132.
[3] 余光识.毫米波MIMO系统低峰均比序列与预编码研究 [D].南京:东南大学,2016.
[4] 马东旭.具有低峰均比特性的序列研究 [D].西安:西安电子科技大学,2019.
[5] ETSI. 5G; NR; Physical Channels and Modulation" ETSI TS 138 211 V15.3.0 [S/OL].Sophia Antipolis:European Telecommunications Standards Institute,2018[2024-07-17].https://www.etsi.org/deliver/etsi_ts/138200_138299/138211/15.03.00_60/ts_138211v150300p.pdf.
[6] 张剑锋.基于CORDIC算法低功耗加速器设计与实现 [D].长沙:国防科学技术大学,2016.
[7] HU Y H. The Quantization Effects of the CORDIC Algorithm [J].IEEE Transactions on signal processing,1992,40(4):834-844.
[8] 陈文俊.基于改进型CORDIC算法的高速DDS设计 [D].武汉:华中师范大学,2021.
[9] HU Y H. CORDIC-based VLSI Architectures for Digital Signal Processing [J].IEEE Signal Processing Magazine,1992,9(3):16-35.
[10] 曲世隽,王翾.一种降低CORDIC算法截断误差的方法 [J].中国传媒大学学报:自然科学版,2021,28(6):53-58.
作者简介:王汉(1991—),男,汉族,河北石家庄人,工程师,硕士,研究方向:卫星移动通信传输技术;通信作者:王力男(1968—),男,汉族,河北石家庄人,研究员,硕士,研究方向:卫星移动通信系统设计。