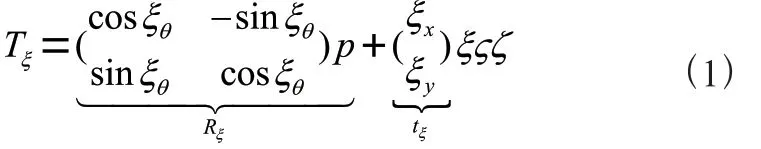

摘 要:作为智能物流系统中重要运输工具的自动引导车(Automated Guided Vehicle, AGV),AGV路径规划与避障算法是移动机器人领域重要研究热点之一。为了解决现有仓储环境下的AGV在运用Q-learning算法进行路径规划时的前期收敛速度慢且探索利用不平衡的问题,提出一种结合引力势场改进Q-learning的算法,同时对贪婪系数进行动态调整。首先,针对传统的Q-learning算法规划时学习效率低问题,构建从AGV到目标点的引力场,引导AGV始终朝着目标点方向移动,减少算法初期盲目性,加强初始阶段的目标性。然后,解决算法探索利用平衡问题,对贪婪系数进行动态改进。仿真实验表明,探索速率提升的同时,算法稳定性也有一定的提升。
关键词:Q-learning算法;强化学习;人工势场算法;AGV;路径规划
中图分类号:TP23;TP18 文献标识码:A 文章编号:2096-4706(2025)02-0171-05
AGV Path Planning Based on Improved Q-learning algorithm in Intelligent Warehouse
GENG Hua, FENG Tao
(School of Information and Electrical Engineering, Hebei University of Engineering, Handan 056038, China)
Abstract: Automated Guided Vehicle (AGV) serves as a crucial transportation means in intelligent logistics systems, and the AGV path planning and obstacle avoidance algorithm is a significant research hotspot in the domain of mobile robots. To tackle the issues of slow convergence speed and imbalanced exploration and exploitation in AGV path planning using the Q-learning algorithm under the existing warehouse environment, this paper proposes an improved Q-learning algorithm combined with gravitational potential field, along with a dynamic adjustment of the greedy coefficient. Firstly, Aiming at the problem of low learning efficiency in traditional Q-learning algorithm planning, it builds a gravitational potential field from the AGV to the target point, directs the AGV to constantly move towards the direction of target point, reduces the initial algorithm blindness, and enhances the targeting performance of initial stage. Next, the algorithm balance problem of exploration and exploitation is solved, and the greedy coefficient is dynamically improved. Simulation experiments demonstrate that while the exploration rate rises, there is a certain enhancement in algorithm stability as well.
Keywords: Q-learning algorithm; Reinforcement Learning; Artificial Potential Field algorithm; AGV; path planning
DOI:10.19850/j.cnki.2096-4706.2025.02.032
0 引 言
随着互联网技术和电商行业的迅速发展,企业对物流搬运、存取货物的效率提出更高的要求。自动引导车AGV(Automatic Guided Vehicle)[1]逐渐应用到物流仓储系统中。AGV的使用不仅提高货物的分拣速度还降低了劳动成本,逐渐实现由“人到货”到“货到人”拣货方式的转变。
AGV的路径规划是指AGV在特定环境下寻找一条从起点到目标点的路径,满足路径长度尽可能短、路径平滑度高,并且能实现AGV的安全避障等要求。路径规划算法主要分为三种:基于图搜索的算法、智能仿生算法和机器学习算法。其中,基于图搜索算法主要有Dijkstar算法、栅格法[2]、A*算法[3]等,但算法进行探索时可能存在内存消耗大、易陷入局部最优等问题,影响路径规划的效果和效率。智能仿生算法通过模拟生物行为进行路径探索,具有较强的适应性和自组织性,算法主要包括:粒子群算法[4-5]、遗传算法[6]、蚁群算法[7]等,但遗传算法进行路径规划时易出现计算量大,易早熟收敛,且参数选择较困难等问题[8]。粒子群算法路径规划适用于全局路径规划并能在复杂环境中找到较优路径,但迭代中对过度依赖参数设置且后期搜索精度不高。机器学习算法在数据处理和模型泛化能力方面表现出色,它能处理大规模数据,挖掘潜在模式且模型具有较好的通用性,代表算法分为两类:强化学习算法[4]、神经网络算法[9],神经网络算法具有强大的鲁棒性及学习力,但是算法泛化能力不强,对样本质量要求过高;强化学习算法通过在环境中“试错”的方式获取环境的反馈信息选择行为,这个特性使得强化学习算法在路径规划时能充分适应动态环境,且具有较好的泛化能力和灵活性。
强化学习算法属于机器学习算法,与监督学习算法不同,强化学习算法无须在有标记的数据集上进行学习,要求AGV通过与环境交互得到奖励选择下一步动作,不断交互迭代来探索最优策略。这使得强化学习算法在毫无先验环境知识的条件下也可进行学习[10]。强化学习算法中,Q-learning算法在空间搜索、非线性控制、路径规划等领域广泛应用[11]。但传统的Q-learning算法在初始化Q值时设置成固定值0,这样会使得算法前无任何先验信息,造成算法初期盲目搜索从而导致收敛速度慢。另外,在探索和利用之间难以平衡也是Q-learning算法的主要问题。
1 相关理论
1.1 Q-learning算法
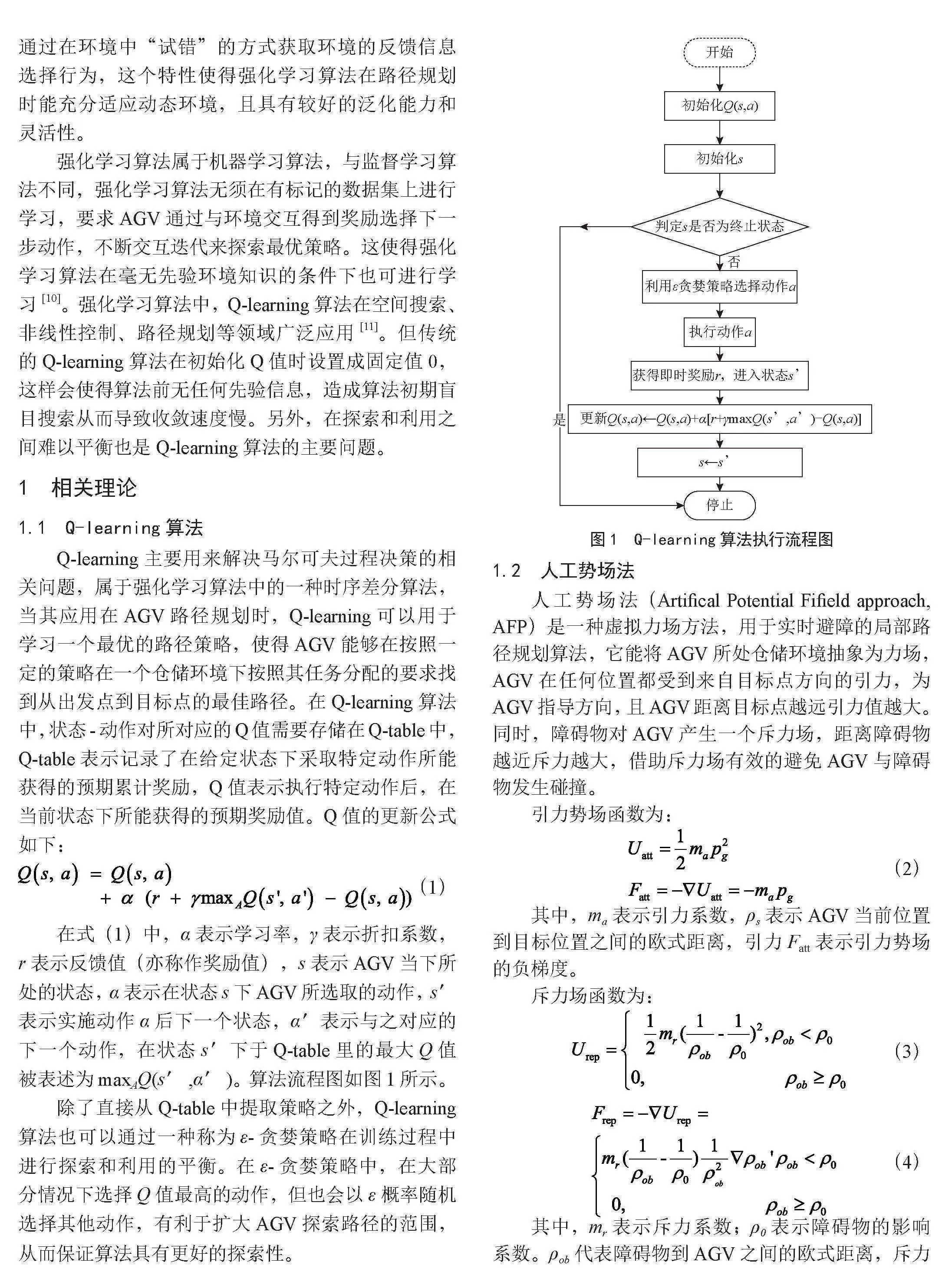
Q-learning主要用来解决马尔可夫过程决策的相关问题,属于强化学习算法中的一种时序差分算法,当其应用在AGV路径规划时,Q-learning可以用于学习一个最优的路径策略,使得AGV能够在按照一定的策略在一个仓储环境下按照其任务分配的要求找到从出发点到目标点的最佳路径。在Q-learning算法中,状态-动作对所对应的Q值需要存储在Q-table中,Q-table表示记录了在给定状态下采取特定动作所能获得的预期累计奖励,Q值表示执行特定动作后,在当前状态下所能获得的预期奖励值。Q值的更新公式如下:
(1)
在式(1)中,α表示学习率,γ表示折扣系数,r表示反馈值(亦称作奖励值),s表示AGV当下所处的状态,α表示在状态s下AGV所选取的动作,s′表示实施动作α后下一个状态,α′表示与之对应的下一个动作,在状态s′下于Q-table里的最大Q值被表述为maxAQ(s′,α′)。算法流程图如图1所示。
除了直接从Q-table中提取策略之外,Q-learning算法也可以通过一种称为ε-贪婪策略在训练过程中进行探索和利用的平衡。在ε-贪婪策略中,在大部分情况下选择Q值最高的动作,但也会以ε概率随机选择其他动作,有利于扩大AGV探索路径的范围,从而保证算法具有更好的探索性。
1.2 人工势场法
人工势场法(Artifical Potential Fifield approach, AFP)是一种虚拟力场方法,用于实时避障的局部路径规划算法,它能将AGV所处仓储环境抽象为力场,AGV在任何位置都受到来自目标点方向的引力,为AGV指导方向,且AGV距离目标点越远引力值越大。同时,障碍物对AGV产生一个斥力场,距离障碍物越近斥力越大,借助斥力场有效的避免AGV与障碍物发生碰撞。
引力势场函数为:
(2)
其中,ma表示引力系数,ρs表示AGV当前位置到目标位置之间的欧式距离,引力Fatt表示引力势场的负梯度。
斥力场函数为:
(3)
(4)
其中,mr表示斥力系数;ρ0表示障碍物的影响系数。ρob代表障碍物到AGV之间的欧式距离,斥力场Frep的负梯度,斥力的方向由障碍物指向AGV。
2 基于改进Q-learning算法的AGV路径规划
2.1 仿真环境构建
2.1.1 栅格图环境
仓储AGV环境仿真采用二维栅格法,如图2所示,此后的路径规划均在此环境地图上进行。使用栅格法能将复杂的环境问题分解成简单问题,适合应用于静态环境的路径规划,且算法计算量小,便于实现。
如图2所示,白色为可通过的无障碍区,实心黑色表示为仓储环境的障碍物区域,每个栅格的边长均为1,在实际情况下,对于某些并不规则的障碍物,按照其最大的边长填充为由网格单元组成的障碍物区域[12]。为简化计算和后期存储,对地图栅格进行编号处理。由左下角开始,建立编号和栅格中心点坐标的对应关系,对应关系坐标公式为:
(5)
式中,mod表示求余运算;i表示栅格的序号;Nx表示栅格的总行数;Ny表示栅格的总列数;fix表示向零方向取整。如图2所示,20×20栅格地图中,栅格的序号从左到右从上到下的顺序为1到400,如可以把第一个栅格设置为初始点,第400个栅格设置为终点即目标点。
2.1.2 确定AGV搜索方向
基于栅格法运用Q-learning算法对AGV进行路径规划时,可以将一个栅格表示成一种状态,同时要定义AGV可以执行的动作,通常有4个动作(上、下、左、右),但在实际中,机器人的运动方向是多样的,因此为了使仿真效果更贴近实际,同时又不过度增加算法的复杂性,本文将AGV运动分为8个方向,即每个方向间隔45°角如图3所示,分为上、下、左、右、右上、右下、左上、左下8个方向。AGV每次步长为1或。
2.2 利用引力场函数改进Q值更新函数
传统的Q-learning算法对Q-table初始化时的默认值设置为0或者随机数。这种初始化方式会导致算法初期大量与目标方向相反的无效迭代,因此在算法进行中引入先验知识,使得算法能够减少前期盲目搜索过程。在Q值更新函数过程中引入引力势场函数Uatt,首先改进势场函数如式(6),其中,η表示引力的影响系数,ρg表示AGV距离目标点的欧式距离,m表示一个正常数。通过改进Q值更新函数(7),来实现Q值的更新。
(6)
(7)
2.3 动态改进贪系数ε
传统的Q-learning算法对AGV进行路径规划时,通常采用ε-贪婪策略来解决探索和平衡利用的问题。探索指的是AGV在选择下一个动作时不遵循算法学习策略,而是根据ε(0<ε<1)概率进行探索其他动作,通过这种方式可以对扩大搜索范围,减少局部最优解发生的概率。利用是指AGV在1-ε的概率下选择动作,并且完全按照Q-learning学习策略选择最优解。通过这种方式优化了Q-learning算法的探索利用平衡问题,但是,传统的Q-learning算法在探索初始阶段,由于不具备先验知识AGV对动作选择比较随机,因此前期需要加大探索的概率,随着算法不断迭代,后期趋于收敛需要多利用,应降低探索的概率。本文对这个问题的贪婪系数进行动态改进。
(8)
上式中,arctan(t)表示反正切函数,其定义域为实数集,值域为(-π/2,π/2)。当t>0时,arctan(t)的取值范围为(0,π/2),Sn表示标准差,表示算法每迭代n次后的平均值与当前的次数差值,迭代步数差别越大标准差Sn就越大,说明算法此时需要加强对环境的搜索,相反Sn越小代表迭代次数之间的步数差距小,说明算法已经越来越趋近收敛,此时算法需要多利用先验知识并减少探索的概率。T表示算法的尺度系数,b表示探索率的最大值,c表示探索率的最小值。
经过改进在Q-learning算法的前期,由于算法未收敛迭代标准差Sn比较大,AGV以b的概率对环境进行探索并选择动作。随着路径算法的进行,AGV通过探索积累了经验,使得Sn不断减小,使得贪婪系数ε在(b,c)之间,Sn低于c,表示算法已经趋于收敛,此时探索概率稳定在c。通过上述算法对贪婪系数ε的动态调整,使得算法初始阶段能够更大概率对环境进行探索,随着算法路径搜索的进行,ε不断减小,算法趋于利用,能够更好的平衡Q-learning算法的探索利用平衡的问题。
3 实验结果及分析
3.1 实验仿真即参数设置
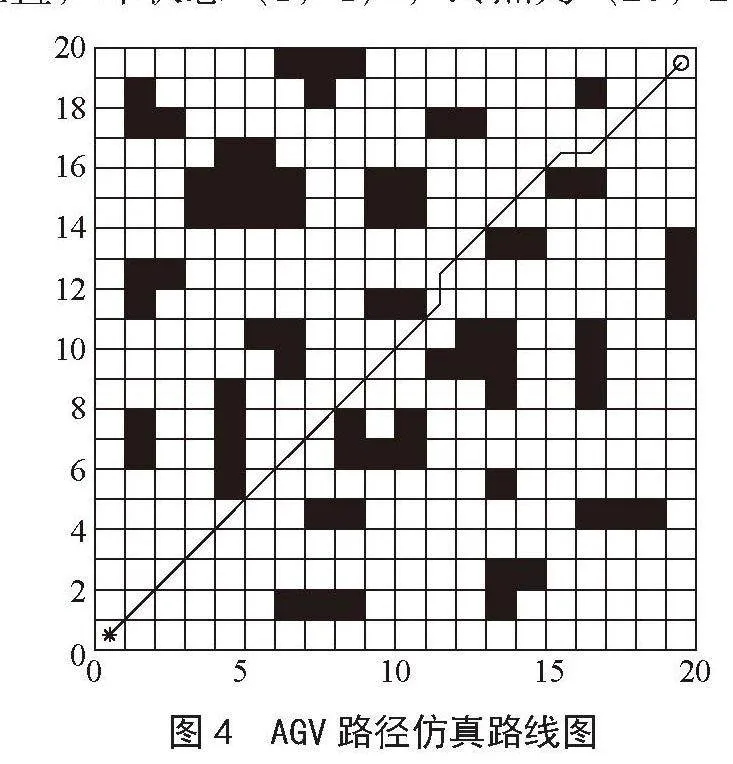
为验证改进后的 Q-learning算法的性能,开展仿真实验。选用MATLAB(R2022a)作为编译工具,在实验中运用栅格地图法对智能仓储AGV环境进行仿真,采用20×20个单位的栅格,以左下角坐标为原点,建立一个水平方向为X轴,垂直方向为Y轴的坐标轴[13]。
如图4所示,其中“*”表示移动机器人的初始位置,“o”表示移动机器人的目标位置,白色部分为自由活动区域,黑色实心方框代表无法穿过的障碍区域[14],移动机器人的动作空间以角度45度为单位的八个方向,即上、下、左、右、左上、右上、左下、右下八个方向。栅格图中共有400个栅格,在Q-learning算法中代表400中状态,起点为(0,0)坐标位置,即状态(1,1),终点为(20,20)。
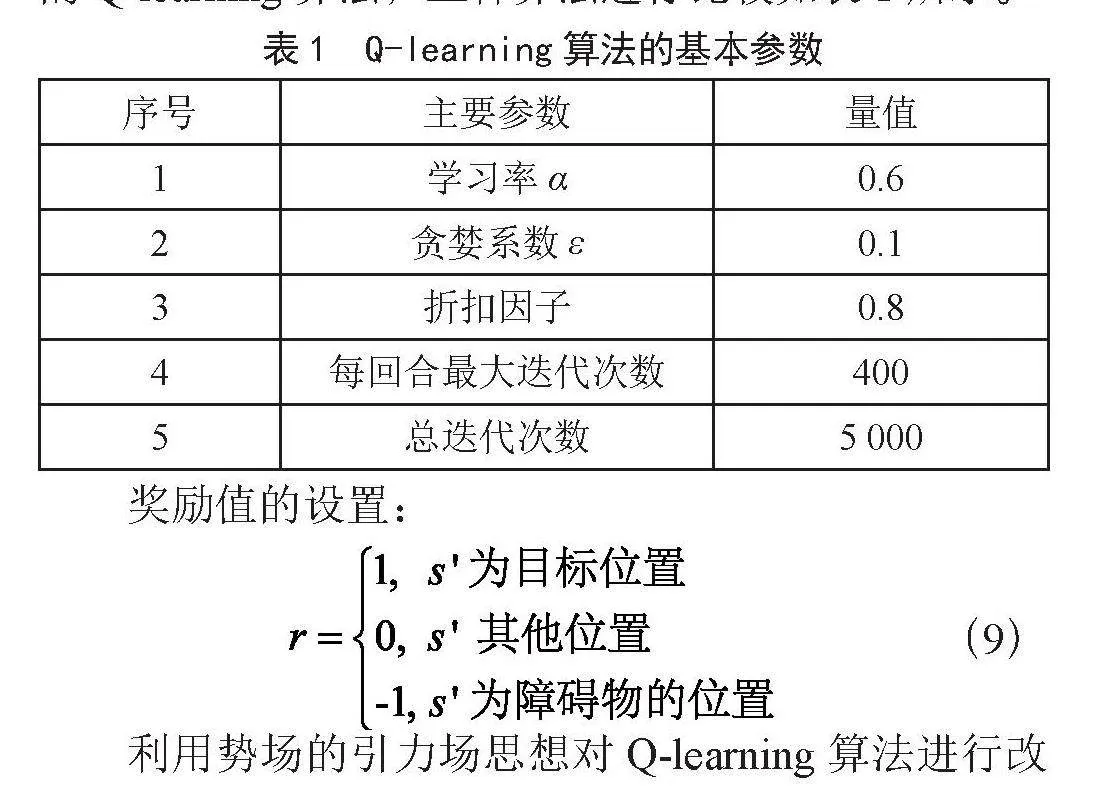
Q-learning算法中,需要首先设定参数,这些参数会影响到最终的收敛。分别对比传统Q-learning算法,优化Q值后的Q-learning算法,加入贪婪系数后的Q-learning算法,三种算法进行比较如表1所示。
奖励值的设置:
(9)
利用势场的引力场思想对Q-learning算法进行改进,中ρg表示距为起点与目标点的欧式距离,势场中的引力系数η = 0.6,常数m = 1;动态改进贪婪系数参数取值:b = 0.6,c = 0.01,T = 1 000,n = 10。
3.2 实验分析
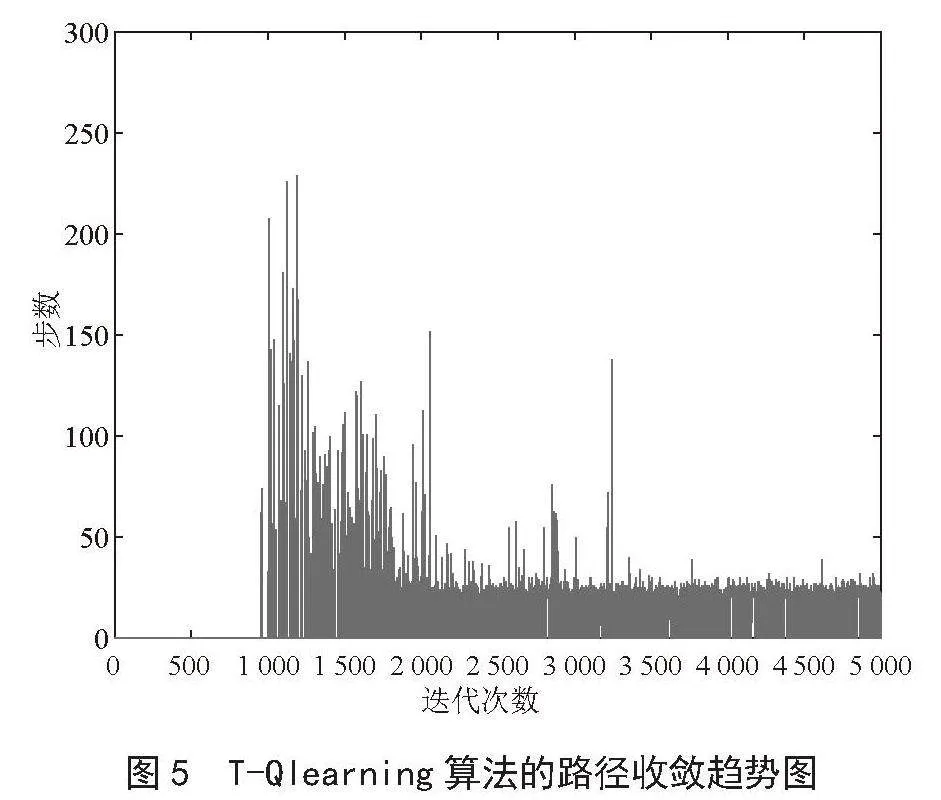
在仿真实验中,图5为传统Q-learning算法的路径规划收敛图,如图5所示在5 000次的探索中,大约在迭代2 000次时算法趋于收敛。运行时间为2.73 s。但前期的算法无效迭代次数过多,导致1 000次左右算法才开始出现成功迭代。后期由于贪婪系数固定值,导致收敛后曲线不平滑。
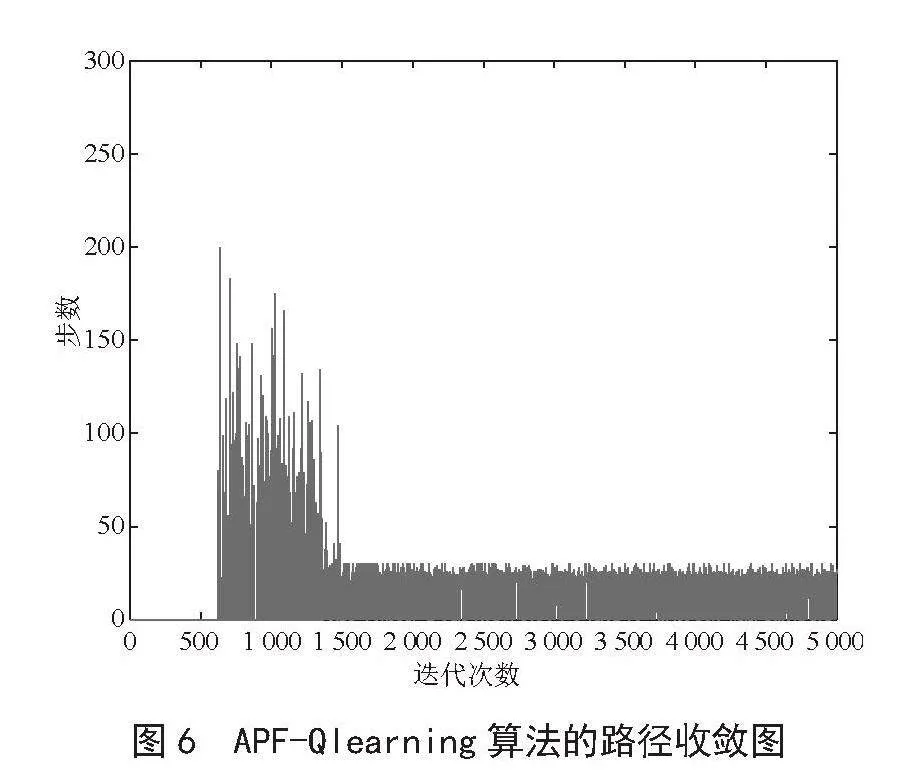
Q-learning算法在引入引力势场函数后(如图6所示),AGV在的方向性更强,始终以较大概率朝着目标点方向行进且减少了盲目搜索次数,与图5相比,引入引力势场函数后算法有效减少了前期的无效迭代次数,由1 000次降到600次左右,收敛次数过程也是逐渐由高到低,同时,引入引力势场函数后,收敛速度也有所提升,在1 500次迭代后趋于收敛。
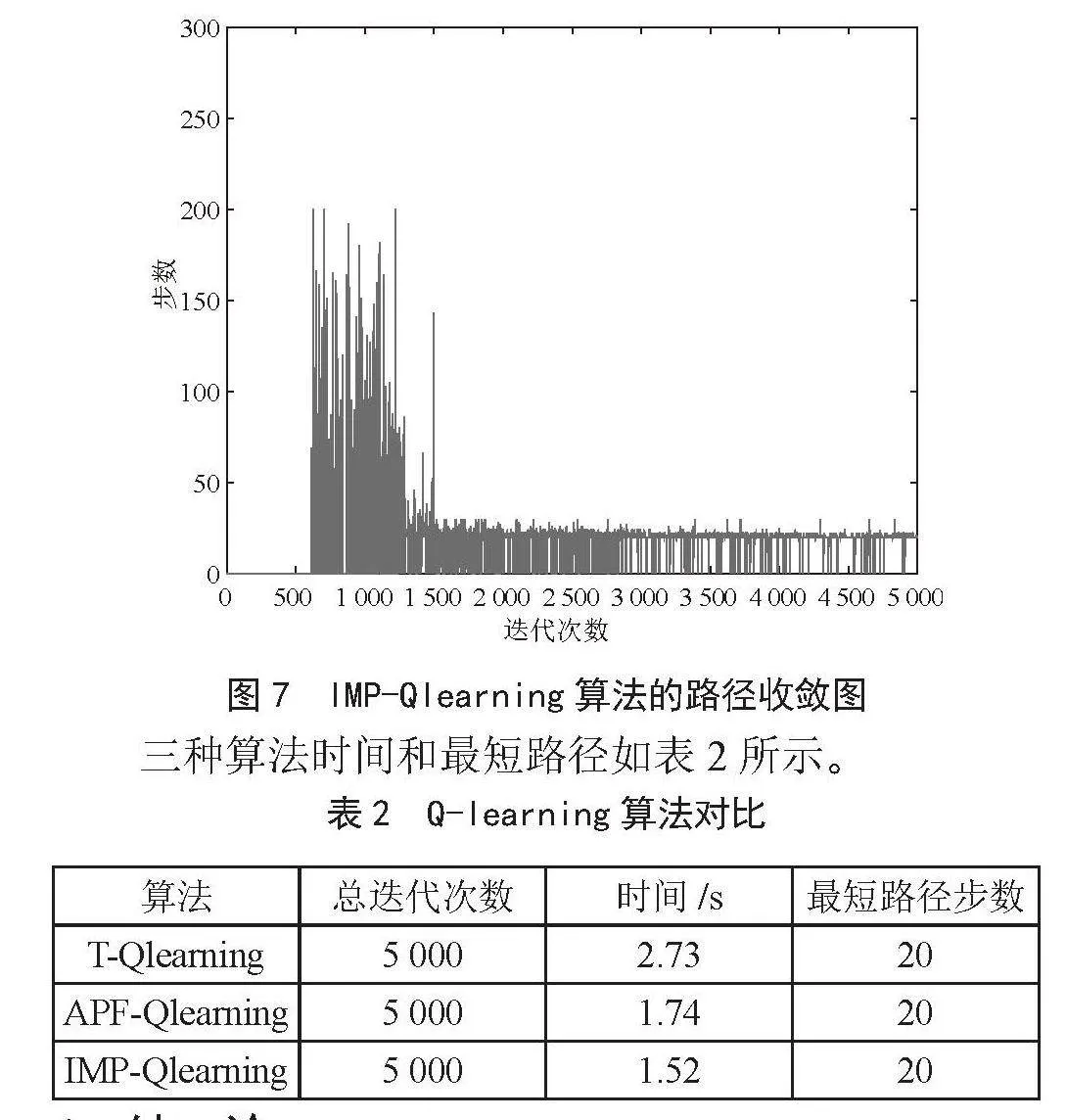
如图7所示,进行完上述改进后,进一步将算法中的贪婪系数ε进行动态调整,早期增加了贪婪系数的值,由固定的0.1上涨到0.6,扩大了对环境的探索,因此迭代次数相较于图6有所增加,在算法运行的后期趋于收敛,贪婪因子减小到接近0.01,使得算法后期趋于利用,减少了探索失败的次数,同时进一步减少了程序的运行时间。
三种算法时间和最短路径如表2所示。
4 结 论
论本文提出一种针对运用栅格法仿真仓储AGV运动环境,对Q-learning算法那进行改进的路径规划算法,算法运用人工势场法的引力势场思想,引入了改进后的引力势场函数改进Q值更新函数,同时,对贪婪系数进行了动态改进,通过实验仿真表明,引入势场函数后的Q-learning算法收敛速度提高,动态改进结果的稳定性增加。但本文只是针对单个AGV路径规划算法,对仓储环境下的多AGV路径规划还需进一步研究。
参考文献:
[1] CHEN X,LIU S,ZHAO J,et al. Autonomous Port Management based AGV Path Planning and Optimization Via an Ensemble Reinforcement Learning Framework [J/OL].Ocean and Coastal Management,2024,251:107087(2024-03-10).https://doi.org/10.1016/j.ocecoaman.2024.107087.
[2] 朱磊,樊继壮,赵杰,等.基于栅格法的矿难搜索机器人全局路径规划与局部避障 [J].中南大学学报:自然科学版,2011,42(11):3421-3428.
[3] 余翔,姜陈,段思睿,等.改进A*算法和人工势场法的路径规划 [J].系统仿真学报,2024,36(3):782-794.
[4] 蔺文轩,谢文俊,张鹏,等.基于分组优化改进粒子群算法的无人机三维路径规划 [J].火力与指挥控制,2023,48(1):20-25+32.
[5] XIN J,LI Z,ZHANG Y,et al. Efficient Real-Time Path Planning with Self-Evolving Particle Swarm Optimization in Dynamic Scenarios [J].Unmanned Systems,2024,12(2):215-226.
[6] 杨海兰,祁永强,荣丹.仓储环境下基于忆阻强化学习的AGV路径规划 [J].计算机工程与应用,2023,59(17):318-327.
[7] CUI Y,REN J,ZHANG Y. Path Planning Algorithm for Unmanned Surface Vehicle based on Optimized Ant Colony Algorithm [J].IEEJ Transactions on Electrical and Electronic Engineering,2022,17(7):1027-1037.
[8] LI D D,WANG L,CAI J C,et al. Research on Path Planning of Mobile Robot based on Improved Genetic Algorithm [J/OL].International Journal of Modeling, Simulation, and Scientific Computing,2023,14(6):2341030[2024-03-16].https://doi.org/10.1142/S1793962323410301.
[9] 徐晓苏,袁杰.基于改进强化学习的移动机器人路径规划方法 [J].中国惯性技术学报,2019,27(3):314-320.
[10] SURESH K S,VENKATESAN R,VENUGOPAL S. Mobile Robot path Planning Using Multi-Objective Genetic Algorithm in Industrial Automation [J].Soft Computing,2022,26(15):7387-7400.
[11] 吉红,赵忠义,王颖丽,等.复杂环境下多AGV路径规划与调度系统研究 [J].机械设计,2023,40(6):110-115.
[12] 王志伟,邹艳丽,刘唐慧美,等.基于改进Q-learning算法和DWA的路径规划 [J].传感器与微系统,2023,42(9):148-152.
[13] 任学干,葛英飞.基于改进势场蚁群算法的AGV路径规划 [J].南京工程学院学报:自然科学版,2021,19(1):36-41.
[14] 段建民,陈强龙.利用先验知识的Q-Learning路径规划算法研究 [J].电光与控制,2019,26(9):29-33.
作者简介:耿华(1985—),男,汉族,河北邯郸人,讲师,博士,研究方向:复杂系统建模与控制;冯涛(1987—),女,汉族,河北邯郸人,硕士在读,研究方向:移动机器人路径规划。
收稿日期:2024-07-12