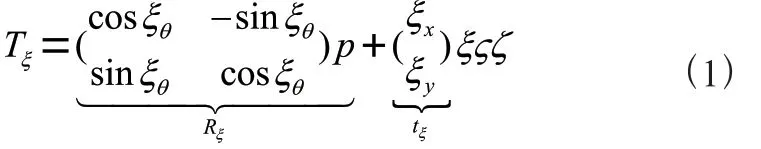



摘" 要:矩阵补全问题可转化为非凸优化问题进行求解,但在高维矩阵或海量数据场景下,传统优化方法易受“维数灾难”制约而难以有效实施。为提升求解效率,文章提出一种融合方差缩减技术的非凸随机优化算法MC_SVR。通过设计minibatch加速策略,该算法在保持计算精度的同时显著提升了运算效率。多组数据集实验表明,相较于传统方法,MC_SVR算法在收敛速度、补全精度等关键指标上均展现出显著优势,尤其在处理大规模矩阵补全问题时,其平均相对误差、迭代次数都有明显的变化。该研究为高维矩阵补全问题提供了新的解决方案,对推荐系统、图像修复等实际应用具有重要参考价值。
关键词:矩阵补全;非凸问题;随机优化;方差减小
中图分类号:TP301.6" 文献标识码:A" 文章编号:2096-4706(2025)04-0103-05
Research on a Matrix Completion Algorithm under the Non-convex Stochastic Optimization Framework
WANG Xuewei1,2
(1.School of Mathematics, Yunnan Normal University, Kunming" 650500, China;
2.Yunnan Key Laboratory of Modern Analytical Mathematics and Applications, Kunming" 650500, China)
Abstract: The matrix completion problem can be solved by transforming into a non-convex optimization problem. However, in high-dimensional matrix or massive data scenarios, traditional optimization methods are easily constrained by “dimension disaster” and they are difficult to implement effectively. In order to improve the efficiency of the solution, this paper proposes a non-convex stochastic optimization algorithm MC_SVR that integrates Variance Reduction technique. By designing the minibatch acceleration strategy, the algorithm significantly improves the computational efficiency while maintaining the computational accuracy. Experiments on multiple sets of datasets show that compared with the traditional method, the MC_SVR algorithm shows significant advantages in key indicators such as convergence speed and completion accuracy. Especially when dealing with large-scale matrix completion problems, the Mean Relative Error and the number of iterations have obvious changes. This study provides a new solution to the problem of high-dimensional matrix completion, and has important reference value for practical applications such as recommendation systems and image inpainting.
Keywords: matrix completion; non-convex problem; random optimization; Variance Reduction
0" 引" 言
随着计算机技术的发展和大数据时代的到来,大规模优化问题日益增多,传统的优化理论和算法每次迭代都要遍历所有样本,难以满足快速求解的需求[1]这促进了随机优化算法的发展。在机器学习领域,随机优化算法在处理大规模数据集时显示出其独特的优势。比如低秩矩阵恢复、线性回归和稀疏字典学习等,但是这些问题可能不是凸的,而非凸问题可能包含多个局部最小值,导致非凸优化问题很难找出全局最优解。这一特性使得非凸优化问题比凸优化问题更加复杂和困难。所以在实际的非凸优化应用中,由于计算资源和时间的限制,通常只能找到一个近似的最优解。
矩阵补全(matrix completion)的理论基础主要来源于压缩感知理论的发展,由Donoho[2]提出的压缩感知技术是信号处理领域的研究热点,其核心思想是基于信号稀疏性,通过低分辨率、欠Nyquist采样数据的非相关观测来实现高维信号的感知。如果将矩阵的低秩性视为矩阵稀疏性,那么向量空间的压缩感知理论就自然拓展为矩阵空间的矩阵补全理论。现如今,随着大规模的数据越来越多,研究者们热衷于对这些大规模数据进行处理,在一些特定应用的领域,矩阵补全技术也受到了越来越多关注,例如在一些特定应用的领域,如矩阵补全理论已在压缩感知[3]、计算机视觉[4]、机器学习[5]、工程控制[6]、子空间聚类[7]等领域均得到了重要应用。为了提高推荐系统的准确性和效率,在矩阵补全技术受到了越来越多关注的同时,也催生了许多关于低秩矩阵补全的经典算法,如SVT[8],近邻梯度下降算法[9](PFBS),加速近邻梯度算法[10](Accelerated Proximal Gradient, APG)等。本文使用随机梯度下降算法和带方差缩减技术的随机梯度下降算法以及对应的小批量算法在人造数据集和真实数据集上进行求解并对其效果进行对比。实验结果表明本文提出的算法在矩阵补全问题中,可以适用于大规模问题求解,可以缓解大规模问题求解上的受限,并且补全性能更好。
1" 矩阵补全模型
假设待恢复的矩阵是低秩矩阵,并且对于这个矩阵假设我们采样到它的其中一部分元素,其他一部分或者大部分元素由于各种原因丢失了或无法得到。从观测到的不完整矩阵最后恢复出原本的低秩矩阵,标准矩阵补全问题可建模为如下形式的秩最小化约束优化模型[11]:
其中Ω为观测到的集合,也就说X中的元素值与观测到的元素值相同。由于秩函数的非凸性和非光滑性,这个问题的求解是一个NP难问题在所有已知的求解算法中,其求解复杂度均随着矩阵维数的增加呈平方倍指数增长[12]。所以我们将上述问题的目标函数用核范数来代替,那么上述的这个问题就转化为了如下的凸问题:
2" 矩阵补全的半正定规划模型
基于上述模型,已经有一些理论结果很好的算法被提出。但是在实际操作中,面对大规模数据,这些算法效率仍然不是很高[13]。另一方面上述模型的求解涉及复杂的奇异值分解,求解效率和可扩放性受限,不适合用于大规模问题且核范数不能紧致地逼近目标矩阵的真实秩[12],所以研究者将问题重写为SDP[14]。
(1)
其中,,V和W为对称矩阵,N为观测值的个数。
将Z分解为Z=VVT(V∈Rn×r),模型转化为如下无约束非凸问题:
记
(2)
算法1" 随机方差缩减的矩阵补全(MC_SVR)算法[15-16]
输入:外循环迭代次数n,内循环次数m,容许误差tol以及初始值 ∈Rn×r
输出:结束算法时内循环最后一次更新的V m
1)在外循环中,,k = 0,1,…,n,计算全梯度∇g(k)。
2)在内循环中,t = 0,1,…,m-1,Z t=V t(V t)T,V 0=k,随机选取it∈{1,2,…,N},计算。
3)计算参考点 。
4)如果,则转到步骤5),否则k = k+1,返回步骤1)。
5)结束算法时内循环最后一次更新的V m。
3" 算法1的收敛性分析
定理(算法1的线性收敛):设为算法1生成的序列,假设1-3均成立且ηk∈(0,ηmax),则以下两点成立:
若,则:
1)是单调递减的。
2)(线性收敛)对于∀k≥1,有以下不等式成立:
若,则∀k∈ℕ,成立。
4" 实验与分析
在本节中,我们将比较随机梯度下降算法和带方差缩减技术的随机梯度下降算法以及对应的小批量算法,所有实验均在MATLAB中运行。
4.1" 人工数据集及参数初始设置
我们首先对人工数据进行实验,我们从矩阵中随机抽取7%的元素作为观察到的结果,得到的显式评分矩阵的稀疏度为7%。其中部分用于训练,其余未观察到的元素将用于测试,实验重复运行10次以获得结果。在不同的算法中,统一参数设置如下:最大迭代次数为950,容许误差为10-8。对于SGD minibatch和MC_SVR minibatch两个算法设置的小批量值为7。
这些人工数据由MATLAB生成。矩阵中观测到的元素是从{1,2,3,4,5}中随机采样,用于模拟用户打分,未观测到的元素由0填充。
4.2" 真实数据集选取及参数初始设置
然后在公开MovieLens数据集上运行我们的实验,我们将观测到的部分数据用于训练,其余用来测试,并且将实验重复运行10次得到结果。
我们选择的真实数据集通常被用在推荐系统中[17],这两个数据集来自(https://grouplens.org/data sets/movielens/)。将MovieLens上的两个不同大小的数据集的信息整理如表1所示。
4.3" 性能评价指标
在实验中,最终迭代结果的目标函数值越低,表明对原问题的求解效果越好。
均方根误差(Root Mean Square Error, RMSE)是一种常用的衡量预测模型在连续性数据上的预测精度的指标。它通过计算预测值与真实值之间的差异的平方和,然后取平均值的平方根来得出,均方根误差的定义如:
其中,yi为第i个观测点的预测值,bi为第i个观测点的真实值,N为观测点的数量。RMSE的值越小,表示模型的预测越准确,效果越好。
4.4" 实验结果分析
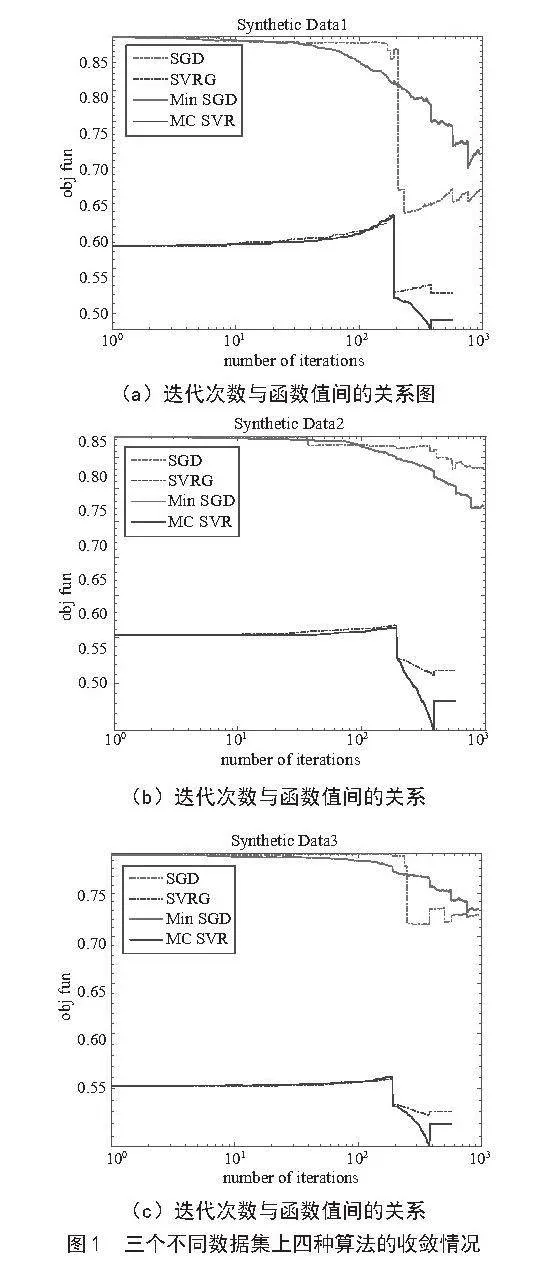
在三个不同大小的人工数据集上运行随机梯度下降算法(SGD)、方差缩减算法(MC_SVR)以及对应的小批量算法,由图1可得,方差缩减算法迭代次数更少达到跳出准则,并且小批量的方差缩减算法(MC_SVR minbatch)能在更少的迭代次数下,目标函数值下降到最低,并且RMSE最小,如表2所示。
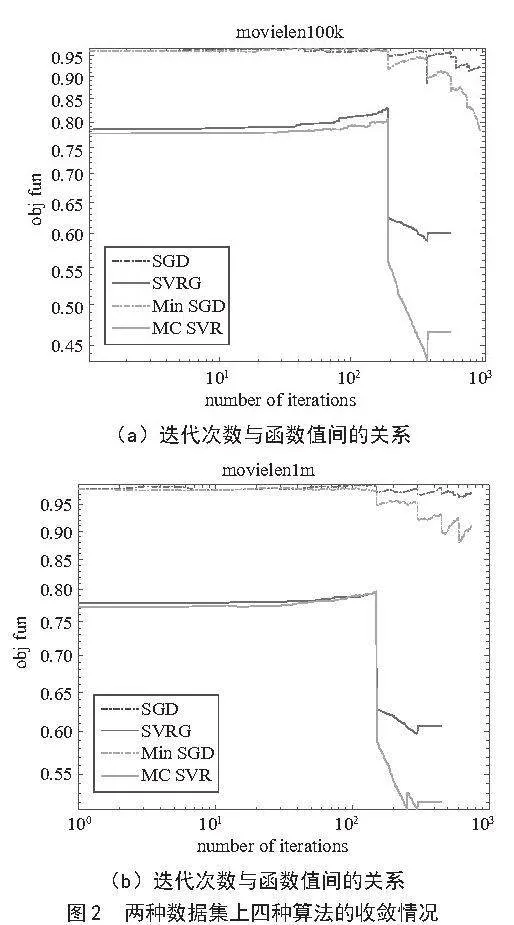
在两个不同大小的真实数据集上运行随机算法,由图2可得,方差缩减算法迭代次数更少达到跳出准则,并且小批量的方差缩减算法(MC_SVR minbatch)能在更少的迭代次数下,目标函数值下降到最低,并且RMSE最小。
从表2可以看出,两种带有方差缩减的随机算法的测试均方根误差比SGD和SGD minbatch SGD这两种算法的更小,其中带有小批量MC_SVR算法又更优于SVRG算法。
同样的,从表3可以看出,两种带有方差缩减的随机算法的测试均方根误差比SGD和SGD minbatch这两种算法的更小,其中带有小批量MC_SVR算法又更优于SVRG算法。
5" 结" 论
将矩阵补全的标准问题形式转化为非凸优化问题,将随机优化算法运用在对应的问题形式中,在不同的数据集上运行实验,实验结果表明小批量的方差缩减算法相比于其他算法在训练集和测试集上具有更小的均方根误差和更小的目标函数值,所以本文所提出的MC_SVR、MC_SVR minibatch算法具有更明显的优势。
参考文献:
[1] 朱小辉,陶卿,邵言剑,等.一种减小方差求解非光滑问题的随机优化算法 [J].软件学报,2015,26(11):2752-2761.
[2] DONOHO D L. Compressed Sensing [J].IEEE Transactions Information Theory,2006,52(4):1289-1306.
[3] LUO Z P,MA J S,SU P,et al. Digital Holographic Phase Imaging Based on Phase Iteratively Enhanced Compressive Sensing [J].Optics letters,2019,44(6):1395-1398.
[4] NEUS G,FELIX P,TOBIAS G,et al. Combining Dielectrophoresis and Computer Vision for Precise and Fully Automated Single-Cell Handling and Analysis [J].Lab on a chip,2019,19(24):4016-4020.
[5] WOLFF P,RÍOS S A,GONZÁLES C. Machine Learning Methods for Predicting Adverse Drug Reactions in Hospitalized Patients [J].Procedia Computer Science,2023,225:22-31.
[6] LEI Z C,ZHOU H,HU W S. Combining MOOL with MOOC to Promote Control Engineering Education: Experience with NCSLab [J].IFAC PapersOnLine,2019,52(9):236-241.
[7] PENG X,TANG H J,ZHANG L,et al. A Unified Framework for Representation-Based Subspace Clustering of Out-of-Sample and Large-Scale Data [J].IEEE transactions on neural networks and learning systems,2016,27(12):2499-2512.
[8] CAI J F,CANDÈS E J,SHEN Z W. A Singular Value Thresholding Algorithm for Matrix Completion [J].SIAM Journal on Optimization,2010,20(4):1956-1982.
[9] COMBETTES L P,WAJS R V. Signal Recovery by Proximal Forward-Backward Splitting [J].Multiscale Modeling amp; Simulation,2006,4(4):1168-1200.
[10] BECK A,TEBOULLE M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems [J].SIAM Journal on Imaging Sciences,2009,2(1):183-202.
[11] CANDÈS J E,RECHT B. Exact Matrix Completion Via Convex Optimization [J].Foundations of Computational Mathematics,2009,9(6):717-772.
[12] 陈蕾,陈松灿.矩阵补全模型及其算法研究综述 [J].软件学报,2017,28(6):1547-1564.
[13] 王川龙,张璐璇.一种求解低秩矩阵补全的修正加速近端梯度算法 [J].忻州师范学院学报,2024,40(2):1-4.
[14] HU E L,KWOK J T. Low-rank Matrix Learning Using Biconvex Surrogate Minimization [J].IEEE Transactions on Neural Networks and Learning Systems,2019,30(11):3517-3527.
[15] 刘浩洋,户将,李勇锋,等.最优化:建模,算法与理论 [M].北京:高等教育出版社,2020.
[16] ZENG J S,MA K,YAO Y. Finding Global Optima in Nonconvex Stochastic Semidefinite Optimization with Variance Reduction [J/OL].arXiv:1802.06232 [math.OC].[2024-08-16].https://arxiv.org/abs/1802.06232.
[17] 吴浩萌.推荐系统中的深度矩阵分解方法研究及应用 [D].长春:吉林大学,2022.
作者简介:王学伟(2000—),男,汉族,四川南充人,硕士在读,研究方向:机器学习方面的研究。
收稿日期:2024-09-04
基金项目:云南省现代分析数学及其应用重点实验室基金资助(202302AN360007);国家自然科学基金项目(62266055)