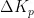
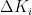
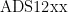
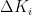
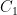
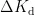
中图分类号:TP216;TP273 文献标识码:A 文章编号:2096-4706(2025)08-0020-05
Abstract: When conducting scientific research on instrumentation,a stable and wel-performing power supplyoften makes theexperimentachieve twicetheresultwithhalftheefort.Atpresent,thedomesticmarkethasalargedemandforhgh-precision four-quadrantpowersupply.Basedonthisbackground,ahigh-voltagendhigh-precisionfour-quadrantpowersuplybasedon fuzzyPIDis designed.Inthis paper,the methodofcombining hardwareclosed-loowithsoftwareclosed-loopisadopted,which greatlyimprovesthe effctiveness ofthe measurementresults.The software controllopuses 24-bitADCchipADS12xx and 24- bit DACchip PCM17x.The hardwareclosed-loop is realizedbybuildinga hardware PIDcircuit.Through experimental tests, theoutput voltage meets expectations,anditiscontinuouslyadjustableinthefour gears ofmediumvotageandhighvoltage,and the voltage ripple is below 0 . 4 V. (20
Keywords: fuzzyPID;four-quadrant power supply; closed-loopcontrol; high-voltage and high-precision
0 引言
随着科学技术的快速发展,电子产品对人们的生产生活起着无法取代的地位[]。在进行科学研究的时候,供电设备性能的优劣对测量结果的准确性有直接影响。
目前我国传统电源种类繁多,电源的产生原理主要有两种,即线性稳压电源和开关电源[2]。这两类电源的工作机制有所不同。线性稳压电源是依据三极管之间的电压波动来维持输出电压的稳定性,虽然它在输出电压稳定性方面表现较好,但工作效率问题不容忽视,在高功率应用场景中尤为明显;开关电源则是通过快速切换功能管在饱和区和截止区的状态,来保持输出电压稳定。这种通过切换将输入电压转换为所需输出电压的方式,效率较高,然而不足之处在于输出电压含有噪声,纯净度欠佳[3-4]。
上述两类主流电源能够提供几百伏甚至上千伏的电压,但电流和电压只能从正向负流动,无法反向流动。这种单向性限制了它们的应用场景。若使用传统电源要在第三象限输出,必须通过反接的方式来达成。然而,常规电源无法实现第二、四象限的输出[5。鉴于此,本文依据当前电源发展历程,提出一种四象限电源[4],旨在解决传统电源电流电压只能单向流动的问题。该设计可使电源在四个象限内工作,如在电池充放电测试中,能够提供或吸收功率,进而简化测试过程[。
1总体方案设计
图1为本设计的总体设计框图,本设计主要分为硬件模拟电路、数字电路以及上位机发送指令三个部分。其中,模拟电路包括硬件PID环、线性放大电路、输出电路、取样电路;数字电路包括数模转换器(DAC)、模数转换器(ADC)。首先,上位机向微控制器发送指令,微控制器接收到指令后对数据进行处理,通过DAC将数字量转换为模拟量,并输出给PI控制器。PI控制器输出模拟量电压值,该值经线性放大电路、输出电路、输出电压,此时输出的是一个中高压值。输出电压经过由精密电阻构成的取样电路,得到一个按比例缩放且可被ADC采集的模拟量电压值。这个模拟量电压值代表经过缩放后的实际电压输出值,将其与DAC基准值进行比较,得出误差电压值并提供给PI控制器进行调节,由此构成一个硬件闭环。另一方面,实际电压输出值会被模数转换器ADC采集数据,采集到的数据送入微控制器进行模糊处理,得到一个理论值。该理论值会被转换为模拟量,即前文所述的基准值,进而构成软件闭环。此外,外部会提供一个正负电压,通过继电器实现不同电压量程的切换,利用光耦将数字信号和模拟信号进行隔离。
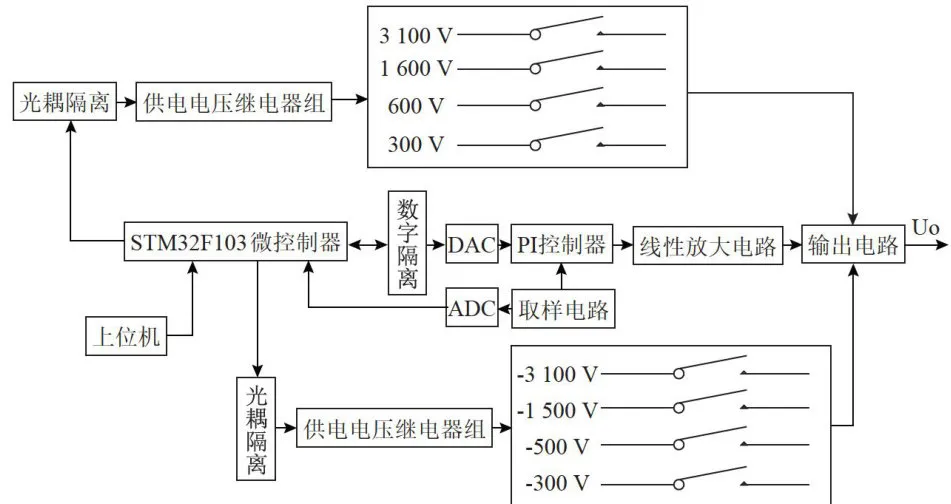 图1系统总体设计框图
图1系统总体设计框图
采用这两种闭环控制方式,能够有效减小误差,确保输出电压的稳定性。外围软件闭环采用模糊控制算法,这是由于本设计电路需实现高压输出,其电路系统极为复杂,且并非依据常规数学模型运行,很难用一个具体的模型来加以描述。而模糊控制恰好能弥补这一不足,该模糊控制算法具备更优的动态特性和更高的控制精度,使用起来更为灵活,适应性更强[3]。硬件方面采用PI控制器进行误差调节,利用分立元件搭建而成,通过修改元器件参数,能够较为精准地缩小误差。将硬件PID与软件模糊PID控制方式相结合,可充分发挥硬件实时响应能力强和软件高度灵活的优势,确保系统既能快速适应变化,又能实现智能优化。表1展示了四象限电源的预期性能指标。该四象限电源能够在四个量程下实现正负电压输出,分别为 ± 2 0 0 V 、 ± 5 0 0 V 、 ± 1 5 0 0 V 、 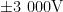 ,输出电压精度达五位半。
,输出电压精度达五位半。
 表1四象限电源技术指标
表1四象限电源技术指标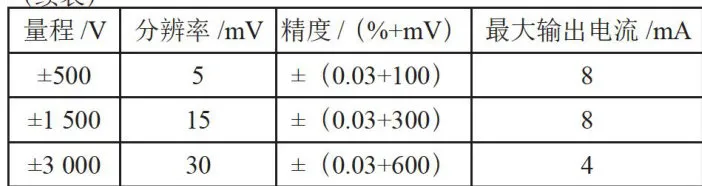 (续表)
(续表)2 模拟电路设计
基本比例-积分控制电路如图2所示,该电路由运算放大器、电阻以及电容构成,实现过程较为简便。采用硬件PID控制方式,能够实时对输入的误差值进行调整。由此,系统响应迅速,且不会占用中央处理器(CPU)资源,进而提升输出电压的稳定性。当输出电压值小于系统预设电压值时,系统会增大输出;当输出电压值大于系统预设电压值时,系统则会减小输出[4]
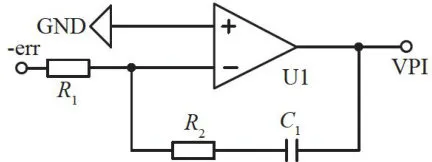 图2基本比例-积分控制电路
图2基本比例-积分控制电路PI控制器将比例 ( P )与积分 ( I ) 两种控制方式相结合,只需调整 P 和 I 的比例系数,便能优化系统性能。在图2中,-err代表该系统的输入信号(反馈输出与预设值的差值),VPI表示系统输出信号。运算放大器U1的同相输入端电压为 0 V ,依据运放的虚短特性,可得出式(1)、式(2):
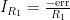
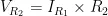
根据运算放大器的虚断特性可知,电流 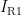 仅能流经
仅能流经 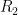 和
和 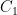 串联的支路,无法进入运放的反相输入端,因此电阻
串联的支路,无法进入运放的反相输入端,因此电阻 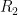 、电容
、电容 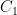 两端的电压表达式如式(3)、式(4)所示:
两端的电压表达式如式(3)、式(4)所示:
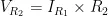
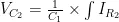
输出电压 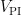 如式(5)所示:
如式(5)所示:
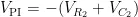
整理可得:
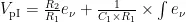
因此,根据式(6)可得出 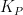 、
、 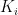 比例积分系数的结果表达式,如式(7)、式(8)所示:
比例积分系数的结果表达式,如式(7)、式(8)所示:
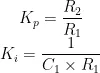
式(6)可改写为:
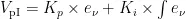
由此,根据式(6)和式(9)可推导得出:在实际应用中,通过设定 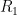 、
、 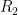 、
、 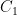 的具体数值,便能对比例-积分控制电路中
的具体数值,便能对比例-积分控制电路中 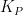 和
和 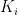 的参数进行调整。这样,直接借助调整元器件参数的方式优化系统性能,能够保障输出电压的稳定,进而确保系统的稳定性与准确性。图3展示了具体电路的设计参数。
的参数进行调整。这样,直接借助调整元器件参数的方式优化系统性能,能够保障输出电压的稳定,进而确保系统的稳定性与准确性。图3展示了具体电路的设计参数。
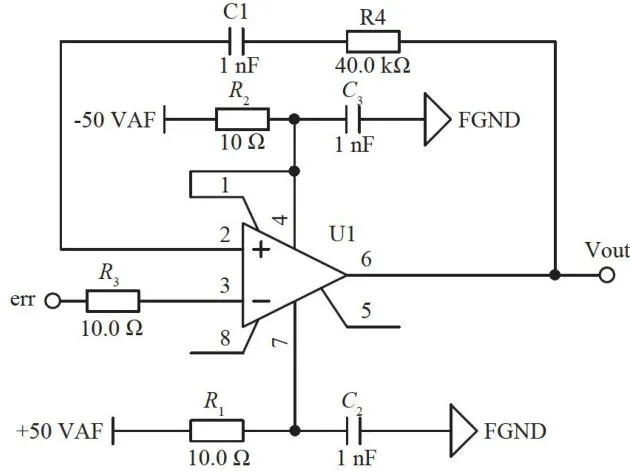 图3具体电路设计参数
图3具体电路设计参数3 软件部分设计
3.1 传统PID算法
软件层面的PID控制算法是当前应用最为广泛的算法之一,该算法发展时间较早,控制理论相对成熟[7。其中,PID控制器可表述为:
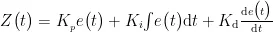
由于本系统以STM32F103微控制器作为主控制器,其处理的是数字量,因此需对式(10)进行改写,将其转换为离散状态下的数学表达式,具体为:
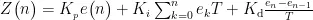
再次对式(11)进行改写,得出:
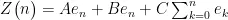
式(12)为位置式PID,通过调节A、B、C系数,能够改变系统的动态响应。鉴于PID的每次输出均与前一次的误差相关,因此对式(12)加以改写,得到:
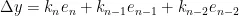
式(13)为增量式PID公式,从中可知系统电压输出仅与最近三次的采样值相关。然而,由于本电路系统极为复杂,难以归纳出一个精确的数学模型,故而提出将传统PID控制方法与模糊PID相结合的方案。
3.2模糊PID控制算法
软件部分是在传统PID控制算法的基础上引入模糊控制。模糊控制是一种基于模糊集合理论的控制策略,它巧妙地以模糊理论、模糊语言变量以及模糊逻辑作为数学基础,进而形成了一种独特且具有创新性的计算机控制算法[8。这种控制方法不仅能够有效处理不确定性和模糊性问题,还能显著提升控制系统的鲁棒性和适应性,具备抗干扰能力强、响应速度快的优势,使其在复杂多变的环境中表现出色。
此外,模糊控制本质上是一种非线性控制。该控制方法基于知识(规则)乃至语义描述的控制规律得以实现,这为非线性控制器提供了一种相对简便的设计途径[。尤其当被控对象存在不确定性,且难以运用传统的非线性控制理论进行有效处理时,模糊控制展现出更为显著的优势与效能[8]。
图4为模糊PID控制的原理框图。首先,系统存在一个参考值,反馈回来的信号与参考值进行差值运算,从而得到误差信号。其次,误差信号 e 和误差变化率ec被输入至模糊控制器,经过模糊化处理后得到 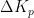 、
、 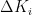 :
: 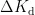 ,再次,利用模糊推理机制得出模糊控制算法,将
,再次,利用模糊推理机制得出模糊控制算法,将 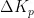 、
、 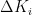 、
、 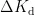 和原有的
和原有的 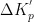
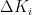 ,
, 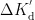 依次叠加,以此实现参数自整定[9-]。从图4可以看出,完成模糊化处理后得到比例、积分、微分系数,这三个参数被代入PID控制器进行再次处理。此过程类似于一个并行结构,再次运算后,得到的输出结果被输送给执行单元,经主电路输出,得到输出结果
依次叠加,以此实现参数自整定[9-]。从图4可以看出,完成模糊化处理后得到比例、积分、微分系数,这三个参数被代入PID控制器进行再次处理。此过程类似于一个并行结构,再次运算后,得到的输出结果被输送给执行单元,经主电路输出,得到输出结果 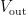 。输出结果再反馈回去与基准电压进行比较。
。输出结果再反馈回去与基准电压进行比较。
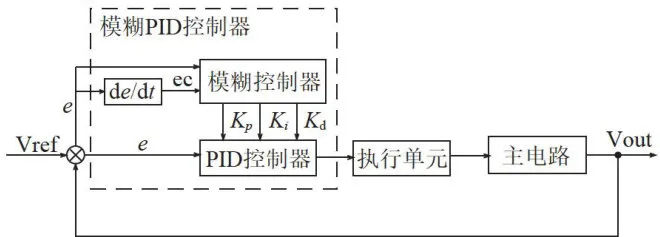 图4模糊PID控制框图[12]
图4模糊PID控制框图[12]
模糊PID的输出参数分别是 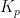 ,
, 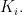 ,
, 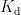 ,其结果如式(14)、式(15)、式(16)所示,其中,初始整定参数为
,其结果如式(14)、式(15)、式(16)所示,其中,初始整定参数为 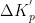 、
、 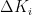 、
、 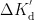 ,用
,用 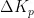 、
、 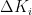 ,
, 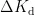 表示参数的变化量。
表示参数的变化量。
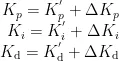
一般情况下,高斯函数和三角形函数作为模糊子集的隶属度函数会有着较好的控制效果,如图5所示。
将论域设置为[-1,1],论域的子集分别设置为[NB、NM、NS、Z、PS、PM、PB],同时,模糊推理过程如图6所示。这样的选择旨在优化模糊PID在实际系统中的应用效果。
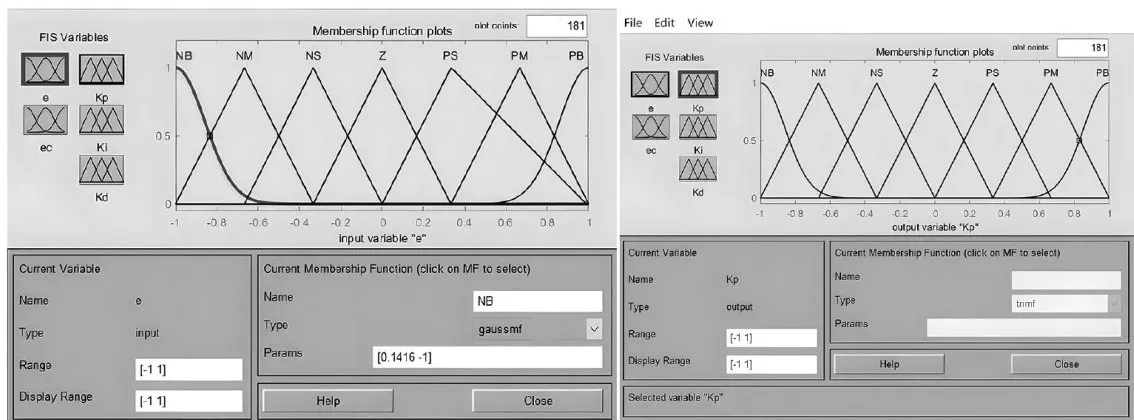 图5隶属度函数
图5隶属度函数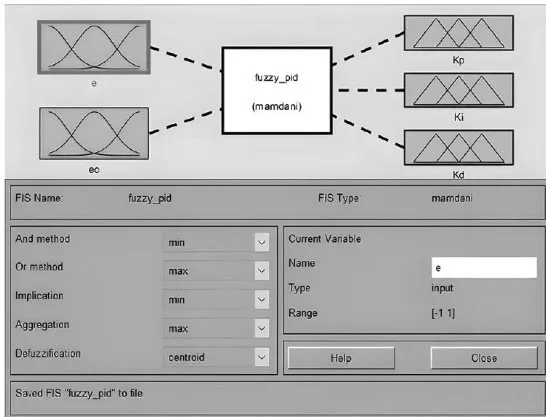 图6模糊推理
图6模糊推理
根据专家经验获取 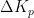 、
、 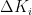 和
和 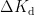 模糊规则表,根据模糊规则表的结果不同,得到不同的电源动态性能,输出程序流程图如图7所示。
模糊规则表,根据模糊规则表的结果不同,得到不同的电源动态性能,输出程序流程图如图7所示。
开始 读取AD的值计算误差调用PID算法结束
4实验结果分析
采用硬件PI控制和软件模糊控制相结合,可实现多量程下的电压输出,并且输出精度为5位半。衡量输出电压是否达到理想预期,可利用稳定度来衡量,具体计算如式(17)所示。在PC端界面输入给定的理想电压值,数字万用表测量输出电压值,根据输出电压的最大值和最小值计算输出电压的稳定度,进而得到表2的结果。
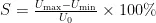
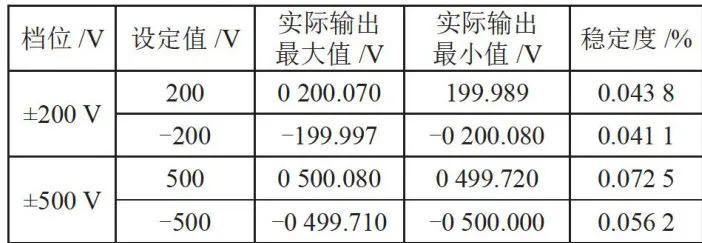 表2不同档位下电源输出值与准确度
表2不同档位下电源输出值与准确度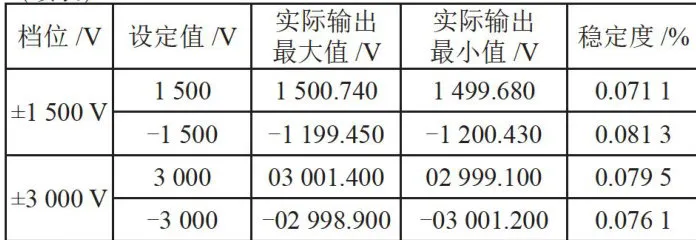 (续表)
(续表)
本设计分别对四个不同量程的电压进行测量,在每个量程内分别选择中间值和极限值进行测量。输出电压的稳定度达到 ± 0 . 1 % ,纹波电压在 0 . 4 V 以下。输出电压的范围在 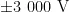 可调,达到了预期的实验结果。但在实验过程中也存在不足:当输出电压在 5 0 0 V 以下时,输出电压的稳定度性能良好;而当输出电压超过 5 0 0 V 时,系统的稳定性相对变差,这可能是由于供电设备的电源存在纹波所致。
可调,达到了预期的实验结果。但在实验过程中也存在不足:当输出电压在 5 0 0 V 以下时,输出电压的稳定度性能良好;而当输出电压超过 5 0 0 V 时,系统的稳定性相对变差,这可能是由于供电设备的电源存在纹波所致。
5结论
通过实验验证和结果分析,该设计的四象限电源符合理论预期,达到设计要求。本设计的输出电压精度可以达到5位半,这可以简化许多电子测试,具有较好的推广性。除此之外,若想实现更高位数的分辨率,则需要借助软件算法。本设计中,ADC和DAC均为24位,而目前ADC的最大位数也是24位。若能通过软件扩展ADC的位数,进而实现更高分辨率的输出,将有助于推动我国半导体事业的不断发展。
参考文献:
[1]郑清良.现代电力电子技术在开关电源中的应用分析[J].光源与照明,2024(1):171-173.
[2]李星宇.低功耗开关电源模块的研究与设计[D].成都:电子科技大学,2023.
[3]杨卫悦.高压直流电源设计研究[D].天津:天津理工大学,2022.
[4]杨成.高精度的程控直流稳压电源的设计[D].成都:电子科技大学,2020.
[5]龙彦卿.四象限程控信号源模块设计[D].成都:电子科技大学,2021.
[6]郑天云,金佛荣,郑一超.高精度四象限电源的校准原理及方法[J].自动化仪表,2020,41(6):20-23.
[7]BORASERP,MAGHADEDK,SONDKARSY,et al. A Review of PID Control,Tuning Methods and Applications [J]. International JournalofDynamicsandControl,2021,9:818- 827.
[8]乔健,罗磊,托乎提努尔,等.基于模糊PID的真空蝶阀压力控制算法研究[J].真空科学与技术学报,2025,45(1):73-79.
[9]PHUND,HUNGNN,AHMADIANA,etal.ANewFuzzy PID Control System Based on Fuzzy PID Controllerand Fuzzy Control Process [J].International Journal of FuzzySystems,2020,22(7):2163-2187.
[10]CETIN\$,AKKAYAAV.SimulationandHybrid Fuzzy-PID Control for Positioning ofa Hydraulic System[J]. NonlinearDynamics,2010,61:465-476.
[11]罗景亮.基于模糊算法参数整定PID控制的DC/DC变换器研制[D].重庆:重庆理工大学,2021.
[12]莫程凯.数字直流稳压开关电源的设计与实现[D].衡阳:南华大学,2022.
作者简介:鲁燕(1999一),女,汉族,江苏邳州人,硕士研究生在读,研究方向:仪器仪表控制技术、嵌入式。