中图分类号：TP301.6 文献标识码：A 文章编号：2096-4706（2025）08-0165-05
Abstract：Aiming at the problemof course scheduling in collges and universities，this paper proposes a solution based on Genetic Algorithm.Course scheduling is akeytask ineducationmanagement.Itnotonlyaffects theeffciencyofresource utilizationinschols，utalsoisdrectlyrelatedtotheimprovementofeachingquality.Thetraditionalmanualcoursesheduling method is unable tofullconsider various complex constraints，resulting in wasteofresources andfrequent conflicts.Inrecent years，withtheadvancementofcomputing technology，GeneticAlgorithmhasshownsignificantadvantages insolving such problems due toitsstrong robustnessandparalelism.This paperachievesaneffcientandfexiblecourseschedulingbyrationally designingchromosomecoding，ftmess functionand geneticoperation.The experimentalresultsshow thatthe proposed algorithm can quickly converge to the high-quality solution， and has good robustness and flexibility.
Keywords： Genetic Algorithm;course scheduling incoleges anduniversities; multi-constraint optimization;automati course scheduling system
0 引言
排课问题是教育管理中的关键任务，直接影响学校的资源利用效率和教学质量。传统的手工排课方式难以全面考虑复杂的约束条件，导致资源浪费和冲突频发。近年来，随着计算技术的发展，遗传算法因其强大的鲁棒性和并行性，在解决此类问题上展现出了显著的优势。通过编码、选择、交叉和变异等操作，遗传算法能够逐步优化解空间，有效处理多约束优化问题。已有研究显示，结合局部搜索、多目标优化及自适应变异策略的改进遗传算法，能显著提高排课系统的稳定性和效率。例如，张永宏等针对中学走班制设计了一种优化的遗传算法，解决了复杂排课问题[1；朱婷婷提出了一种结合多目标优化和自适应变异策略的改进遗传算法，提高了职业院校自动排课系统的性能[2；郭欣奇探讨了遗传算法参数优化和交叉变异策略，为实际应用提供了指导[3]。此外，徐海涛等探索了基于深度强化学习与遗传算法相结合的方法，实现了排课系统的自学习能力[4。
除了遗传算法，其他优化算法也在排课问题中得到了应用。罗义强等提出了基于改进粒子群算法的高校排课方案[5]，李阳等研究了基于改进遗传算法的高校排课优化问题[。这些研究表明，不同算法在特定场景下具有独特优势。例如，蒋正锋等分别探讨了基于蚁群算法[7和遗传算法[的高校排课问题，指出了各自的应用特点。
从应用场景来看，研究覆盖了从中学到高等教育的不同层次，包括中学走班制、大学课程安排、职业院校排课等。胡秀华等介绍了基于移动平台的高校教务管理系统的设计与实现[，强调了系统在实际应用中的便利性。张宇瞳等专注于天课时分配下的多阶段新高考走班制排课算法[1]，而陈璐等关注的是改进遗传算法求解走班制下的排课问题[]。大多数研究采用了定量方法来验证算法的有效性。例如，张永宏等的研究显示，其提出的算法在实验中成功减少了排课冲突，提高了教室利用率[1。朱婷婷的研究表明，通过引入多目标优化和自适应变异策略，算法在保证课程分布均匀的同时，提升了教师满意度[2。郭欣奇的研究则通过详细的实验数据分析，展示了参数调优对算法性能的影响[3]。这些研究不仅提供了理论上的支持，还通过实验结果证明了算法的实际应用价值。
1排课问题描述
1.1 问题背景
高校排课问题可以形式化为一个组合优化问题，其目标是在满足一系列约束条件下，为所有课程安排合适的教师、教室和时间。具体来说，排课问题可以描述如下：
1）课程信息。每门课程有固定的学时要求，需要分配到特定的时间段。2）教室资源。学校有多个教室，每个教室有一定的容量限制。3）教师资源。每位教师有固定的可用时间段，不能在同一时间教授多门课程。4）班级需求。每个班级有固定的课程表，不能在同一时间上多门课程。5）其他约束。可能还包括教师和学生的偏好、课程的连贯性等。例如，教师可能希望某些课程在特定时间段进行，学生可能希望避免连续的高强度课程，某些课程需要按顺序安排以保证学习的连贯性。
排课目标是确保没有课程在相同的时间段安排在相同的教室、相同的班级或相同的教师，同时尽量考虑教师和学生的偏好，使课程安排更加人性化，提高教学质量和学生的学习体验。
1.2数学模型
1.2.1 决策变量
假设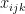 
表示课程 i 是否在时间段 j 安排在教室 k 上课。其中 
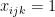表示课程 i 在时间段 j 安排在教室k 上课。 
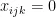表示课程 i 没有在时间段 j 安排在教室k 上课。
1.2.2 参数设置
设课程集为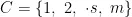 
，时间段集合为
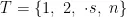，教室集合为 
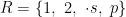班级集合为 
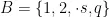，教师集合为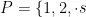 
， 
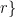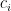为课程 i 所属的班级， 
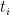为课程 i 所属的教师。
1.2.3 约束条件
模型的约束条件设置如下：
1）每门课程必须安排在某个时间段和教室：
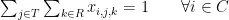
2）同一时间段同一教室只能安排一门课程：
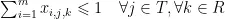
3）同一时间段同一班级只能上一门课程：
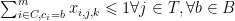
4）同一时间段同一教师只能教授一门课程：
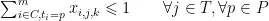
1.2.4 目标函数
定义冲突函数 f （ X ） ，表示所有冲突的数量。目标是使 f （ X ） 尽可能小，理想情况下 f （ X ）=0 。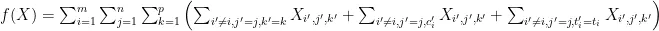
2 遗传算法求解
2.1 染色体编码设计
在遗传算法中，个体的表示（即染色体编码）是解决问题的关键之一。对于高校排课问题，一个合理的染色体编码方案能够有效地表达课程安排，并且易于实现遗传操作。本文采用了一种基于时间槽的编码方式。
时间槽定义：首先将一周的时间划分为若干个连续的时间槽，每个时间槽代表一个可能的上课时间段。例如，可以将一天划分为5个时间槽，那么一周就有25个时间槽。
染色体结构：每个染色体代表一种完整的课程安排方案，由一系列基因组成。每个基因对应一门具体的课程，其值为该课程被安排到的时间槽编号。此外，每门课程还需要额外的信息来指定教室和教师，这些信息可以作为基因的一部分，或者通过其他数据结构关联起来。
这种编码方式的优点在于它直观地反映了课程安排的情况，同时便于进行交叉和变异等遗传操作。
2.2 适应度函数设计
适应度函数用于评估每个排课方案的质量，它是指导遗传算法搜索过程的重要依据。本研究中的适应度函数综合考虑了硬约束和软约束两方面因素。
硬约束：确保没有任何冲突发生，比如同一教师在同一时间教授多门课程、同一班级或同一教室在相同时间有多个活动等。违反硬约束的解将被赋予极低的适应度值。
软约束：包括但不限于课程分布均匀性、教师偏好、学生满意度等因素。这些软约束虽然不是必须满足的，但它们有助于提高整体方案的人性化水平。例如，如果某位教师希望自己的课程集中在上午，那么当安排符合这一偏好时，可以适当增加适应度分值。
根据上述描述，适应度函数可以表示为一个加权求和的形式，其中每一项代表不同的评价指标。设 F 为适应度函数，适应度函数形式为：
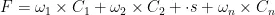
其中，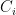 
为第 i 个评价指标（如没有冲突、课程分布均匀性、教师偏好等），而 
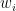为与之对应的权重。具体的 
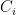定义如下：
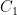为无冲突情况下的奖励，若排课方案中不存在任何时间、教室或教师的冲突，则此值为正；否则为负或0。 
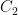为课程分布均匀性的评估，衡量课程在整个周内是否均匀分布，分布越均匀则该值越高。 
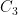为教师偏好的满足程度，依据教师对授课时间段的偏好进行打分，偏好得到满足越多则得分越高。 
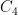为学生学习体验的考量，如避免连续高强度课程，保持课程连贯性等，满足条件则加分。
2.3 求解过程
求解过程如下：
1）初始化。随机生成初始种群，每个个体是一个排课方案，表示为一个三维矩阵。
2）适应度评估。计算每个个体的适应度值，包括硬约束（无冲突）和软约束（课程分布均匀性、教师偏好、学生学习体验等）。3）选择。采用轮盘赌选择或精英选择策略挑选适应度较高的个体进入下一代。轮盘赌选择依据适应度比例；精英选择直接保留适应度最高的几个个体。4）交叉。随机选取两个个体进行交叉操作，通过交换部分基因（如时间段或教室安排）来生成新的个体。5）变异。对新生成的个体执行变异操作，随机改变某些基因以探索新的解空间。6）终止条件检查。检查是否达到最大迭代次数或已找到无冲突的排课方案。如果满足任一条件，则转到结果输出阶段；否则返回适应度评估步骤继续进化。
7）结果输出。将最优排课方案输出至Excel文件中，生成详细的课程表，包含课程名称、上课地点、授课教师等信息。求解过程流程图如图1所示。
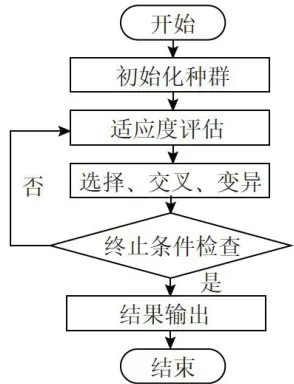图1求解过程流程图3实验设置与结果分析
3.1实验环境与参数设置
本文使用Python实现了基于遗传算法的排课系统，并对其性能进行了测试。硬件配置为：IntelCorei7 CPU，16GBRAM；软件环境为：Python3.9，NumPy，Pandas，Matplotlib。实验参数设置如下：种群规模为32，交叉率为0.7，变异率为0.1，最大进化代数为500代。
3.2 实验数据
本次实验涉及13门课程（如软件工程、数据库原理与应用等），23位教师（每位教师负责不同的课程组合），以及5个计算机班（计算机1班至计算机5班）对这些课程的需求情况。在教室资源方面，假设学校提供了一定数量的教室以满足教学需求。在时间安排方面，每周的教学活动分为5天（周一至周五），每天有5个时间段（第1-2节至第9-10节）。
课程信息表包含以下字段：CourseID（INT，主键）和CourseName（VARCHAR）。教师信息表包括以下字段：TeacherID（INT，主键）、Name（VARCHAR）、Gender（CHAR）、Title（VARCHAR）及一系列布尔字段，表示是否教授特定课程（如Coursel0112）。班级需求表由ClassID（INT，主键）及五个布尔字段组成，分别对应五个计算机班是否需要该课程。课程安排表（Schedules）包括以下字段：ScheduleID（INT，主键）、Section（VARCHAR，节数）、StartTime（TIME）、EndTime（TIME）以及七个布尔字段，表示一周内每天是否有课。
3.3 实验步骤
初始化阶段，算法首先随机生成32个初始排课方案，每个方案详细包含了所有课程的安排信息，确保了种群的初始多样性。随后，进入评估适应度环节，算法会根据每个排课方案对硬约束和软约束的满足情况进行综合评价，计算出适应度值。硬约束主要关注教师、教室、班级之间的时间冲突问题，而软约束则考虑课程分布的均匀性和教师的个人偏好等因素。接下来是选择操作，依据计算出的适应度值，算法会选择保留那些适应度较高的个体，以此来提高下一代种群的质量。紧接着，对选出的高适应度个体执行交叉操作，通过交换部分课程安排信息，生成新的排课方案，这一步骤有助于探索更广泛的解空间。为了进一步增加种群的多样性，防止过早收敛，算法还会对新生成的排课方案进行随机变异操作，即随机调整某些课程的安排。最后，整个过程将循环往复，重复上述的选择、交叉、变异步骤，直到达到预设的最大进化代数（500代）或者满足其他终止条件为止。通过这种不断迭代优化的过程，算法最终能够生成既满足所有硬约束又尽可能符合软约束要求的高质量课程表。
3.4 实验结果
通过实验输出的排课安排表如图2所示，算法收敛图如图3所示。实验结果表明，该算法能够在有限的迭代次数内找到满足所有硬约束的排课方案，同时较好地兼顾了软约束，提高了课程安排的人性化水平。
图2实验输出的排课安排表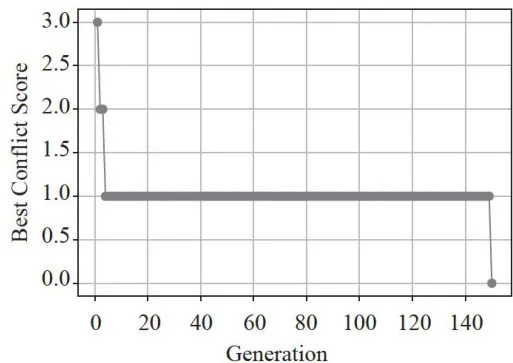
图3算法收敛图该算法在硬约束满足方面表现出色，所有生成的课表均未出现任何教师、教室或班级的时间冲突，确保了课程安排的基本可行性。在软约束满足方面，课程的分布较为均匀，教师的个人偏好也得到了较好地满足，这不仅提高了教师的工作满意度，也有助于提升学生的学习体验。此外，算法的收敛速度非常快，能够在前200代内迅速收敛到一个基本可行的解。之后，随着进化的继续，算法逐渐优化这一解，直至达到最终的优质解。这一特点使得该算法在实际应用中能够高效地生成满意的课程表，为高校的排课工作提供了强有力的技术支持。
4结论
本文成功地将遗传算法应用于高校排课问题，通过合理的设计和优化，实现了高效、合理的课程安排。实验结果表明，该算法能够快速收敛于优质解，并具备良好的鲁棒性和灵活性。尽管如此，本文提出的基于遗传算法的排课系统在实验中表现良好，但仍存在一些局限性和改进空间：在算法参数调优方面，不同场景下，遗传算法的参数（如种群规模、交叉率、变异率等）可能需要进一步调优，以适应不同的排课需求；在多目标优化方面，未来的改进方向可以考虑引入多目标优化技术，同时优化多个目标（如课程分布均匀性、教师满意度、学生满意度等）；
在实时更新方面，在实际应用中，排课系统需要支持实时更新功能，以应对突发情况（如教师请假、教室维修等）。随着人工智能技术的发展，基于遗传算法的排课系统有望在更多的高校中得到应用。未来的研究可以结合机器学习、深度学习等技术，进一步提升排课系统的智能化水平，为高校管理提供更加高效、便捷的解决方案。
参考文献：
[1]张永宏，王永吉，付立军，等.面向中学走班制排课的优化遗传算法[J].计算机系统应用，2020，29（12）：80-86.
[2]朱婷婷.基于改进遗传算法的职业院校自动排课系统研究与实现[D].镇江：江苏大学，2022.
[3]郭欣奇.基于改进遗传算法的排课系统研究与设计[D].哈尔滨：哈尔滨师范大学，2023.
[4]徐海涛，程海燕，童名文.基于深度强化学习的自学习排课遗传算法研究[J].计算机科学，2024，51（S1）：241-248.
[5]罗义强，陈智斌.基于改进粒子群算法的高校排课问题优化[J].计算机应用与软件，2018，35（6）：241-247+303.
[6]李阳，张欣.基于改进遗传算法的高校排课优化问题研究[J].电子科技，2016，29（5）：127-129+138.
[7]蒋正锋，罩韩，吕佩佩，等.基于蚁群算法的高校排课问题的应用研究[J].现代计算机，2019（25）：22-27.
[8]蒋正锋，吕佩佩，覃韩，等.基于遗传算法的高校教务系统排课问题的应用研究[J].现代计算机，2019（21）：32-36.
[9]胡秀华，李承瑞，李桂萍，等.基于移动平台的高校教务管理系统设计与实现[J].软件导刊，2018，17（9）：125-128.
[10]张宇瞳，刘静，郝星星.天课时分配下的多阶段新高考走班制排课算法[J].计算机工程与应用，2021，57（11）：266-278.
[11]陈璐，王秀.改进遗传算法求解走班制下的排课问题[J].计算机工程与应用，2019，55（6）：218-224.
作者简介：燕紫君（1993—），女，汉族，湖北仙桃人，讲师，硕士，研究方向：数据分析、算法研究。
