基于改进DCGAN的毫米波雷达相互干扰时频图像生成研究——以生成样本对CNN干扰抑制模型性能影响为例

陈泽伟，严远鹏

（广东工业大学，广东 广州 510006）

近年来，高级辅助驾驶系统（Advanced Driver Assistance System,ADAS）已经成为汽车无人驾驶的重要基础辅助系统，其涵盖多种多样的功能，如自适应巡航（Adaptive Cruise Control,ACC）、前向碰撞预警（Forward Collision Warning,FCW）、自动紧急制动（Autonomous Emergency Braking,AEB）以及盲点检测（Blind Spot Detection,BSD）等。车载毫米波雷达凭借其优势逐渐成为ADAS 中不可或缺的传感器之一。然而，在一段道路上，当多辆车上装载的多个毫米波雷达系统同时在相近的频段工作时，会造成严重的毫米波雷达相互干扰问题，影响车载雷达的正常探测工作，甚至会因此引发交通事故。

随着近几年深度学习算法的快速发展，用深度学习模型抑制毫米波雷达干扰逐渐成为一个热点研究方向。相比于传统的毫米波雷达干扰抑制方法，在处理更加复杂的多干扰或强干扰场景时，深度学习模型有更大的优势。在时频域中，毫米波雷达的目标信号和干扰信号都被转换为二维图像的特征信息。深度学习模型能够通过对大量数据集的学习，提取毫米波雷达时频图中的目标特征并抑制干扰特征，干扰抑制效果会优于在一维时域信号上处理。Nicolae-Catalin Ristea等人提出了用全卷积网络来处理雷达时频域干扰数据，作者使用仿真数据作为训练数据集，没有实际考虑真实实测数据集对干扰抑制模型的影响，这是因为在实际实验中要测得大量多样性场景的实测数据样本存在一定困难。

生成对抗网络（Generative Adversarial Network,GAN）是由Goodfellow 等人在2014年提出一种无监督深度学习模型，GAN 模型通过不断对抗训练能够生成样本数据。GAN 模型在最近几年受到大量关注并且被运用于图像超分辨率、图像翻译、图像生成等众多不同的图像处理处理领域。然而，尽管GAN 拥有强大的图像处理能力，其同时也存在着模型训练不稳定，容易发生梯度消失甚至模式崩溃等严重问题。针对GAN 存在的众多缺点，研究者们提出了各种改进的GAN 模型。Radford 等人在2015年提出了深度卷积生成对抗网络（Deep Convolutional Generative Adversarial Networks,DCGAN）。DCGAN 模型把卷积神经网络（Convolutional neural network,CNN）和GAN 结合起来，在GAN 的基础上采用了深度卷积网络结构。DCGAN把CNN 在图像特征提取方面的优势和GAN 强大的数据生成能力融合起来，使DCGAN 模型在图像数据的处理能力和稳定生成图像的能力都有了一定程度的提升。但DCGAN 并没有在损失函数做出改进，模型仍然存在训练不稳定，生成图像单一等不足之处。

为了解决在训练深度学习干扰抑制模型过程中实测样本不足的问题，本文提出R-DCGAN（Radar-Deep Convolutional Generative Adversarial Networks）模型来生成毫米波雷达时频图样本。R-DCGAN 在传统DCGAN 的基础上，根据生成毫米波雷达时频图的实际需求，在具体的网络层上做出调整，使用带梯度惩罚项的Wasserstein 距离替代原始的损失函数。带梯度惩罚的Wasserstein 距离克服了原始损失函数容易造成训练过程中梯度消失的问题，同时又避免了WGAN（ Wasserstein GAN）中Lipschitz 约束带来的鉴别器模型参数分布不均问题。R-DCGAN 融合了CNN 的特征提取能力和GAN 的图像生成能力，同时解决了GAN 与DCGAN 模型存在的缺点，能够稳定训练并生成高质量的毫米波雷达时频图数据。

CS（Chirp Sequence）雷达是目前主流的毫米波雷达系统，在CS 雷达中，信号调制方式如图1所示。

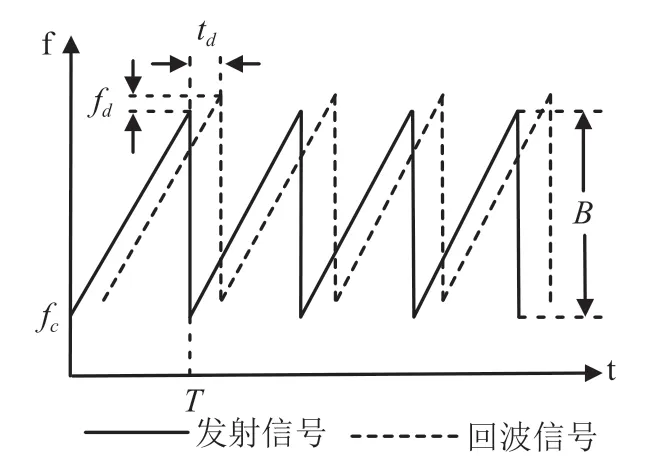
图1 CS 雷达信号调制方式

其中f为信号的载频，f为多普勒频移，t为回波信号时延，是信号带宽，是信号的一个调制周期。发射信号（）的数学表达式为：

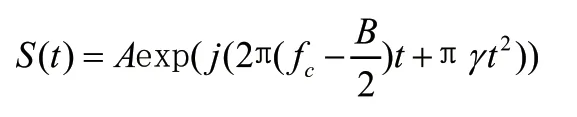
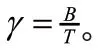
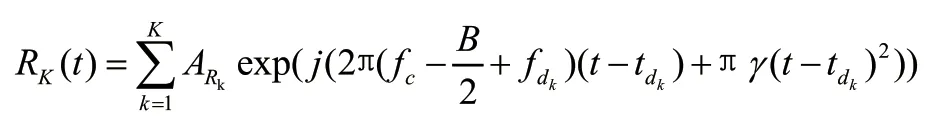
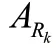
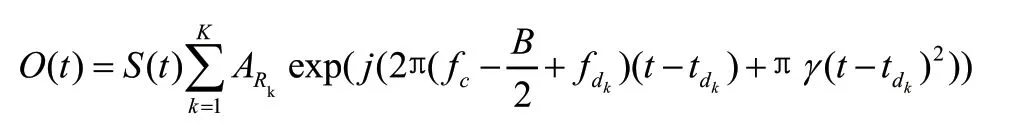
信号（）之后将通过低通滤波器，低通滤波器输出信号的数学表达式可表示为：

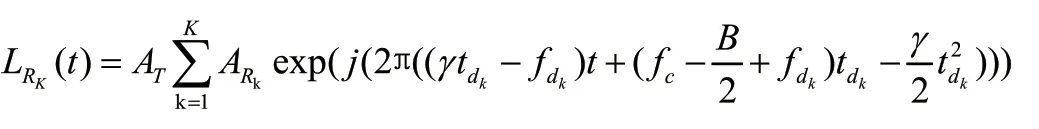
以一个锯齿波调制周期作为研究对象来分析CS 雷达信号受到干扰的数学模型。一个信号周期内雷达发射信号、回波信号、干扰信号以及混频后中频信号的时频关系如图2所示。回波信号和干扰信号会分别和本振信号进行混频，得到各自相对应的中频信号后经过低通滤波器的处理，输出一个受干扰的目标回波信号。图中被测目标物体的中频信号的频率不会随着时间的改变而变化，而干扰中频信号的频率是随时间的变化而变化的。

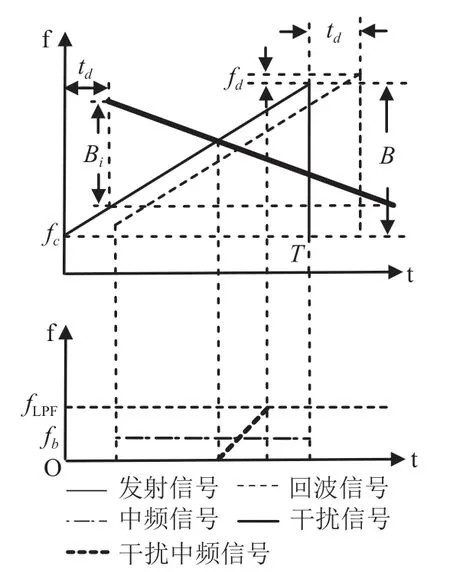
图2 雷达回波信号和干扰信号的时频关系

当存在个干扰源时，干扰信号为：

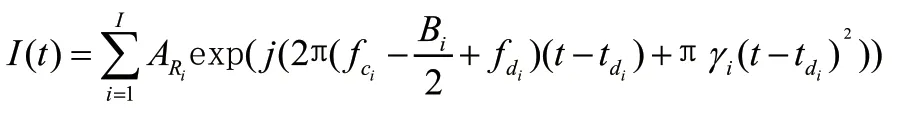
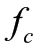
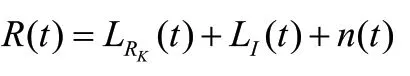
其中（）是噪声信号。L（）是干扰信号（）经过混频器和低通滤波器后的信号，可表示为：

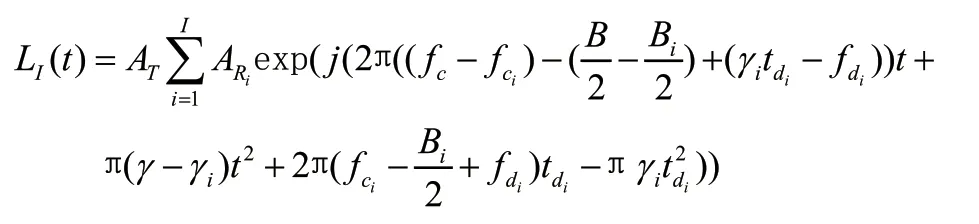
对接收信号做短时傅里叶变换（Short Time Fourier Transform,STFT）得到受干扰接收信号的时频图。在更加复杂的干扰场景中，如在多干扰和强干扰的情况下，CS 雷达相互干扰在时频图中会有更复杂的斜线频率段。如图3所示对比了单干扰、多干扰和复杂干扰场景的时频图。（a）为雷达信号受单干扰情况的时频图，（b）为受多干扰情况的时频图，（c）为受多干扰和强干扰场景的时频图。从受干扰信号的时频图中可以看到目标信号与复杂干扰信号形成相对复杂的相互交叉情况，但是由于目标信号的频率成分不会随着时间变化，所以仍然可以从对应的频率轴上清晰得知目标信号具体频率值信息。干扰信号出现的时间段，干扰频率因随时间的变化而呈现出高度的随机性和复杂性。

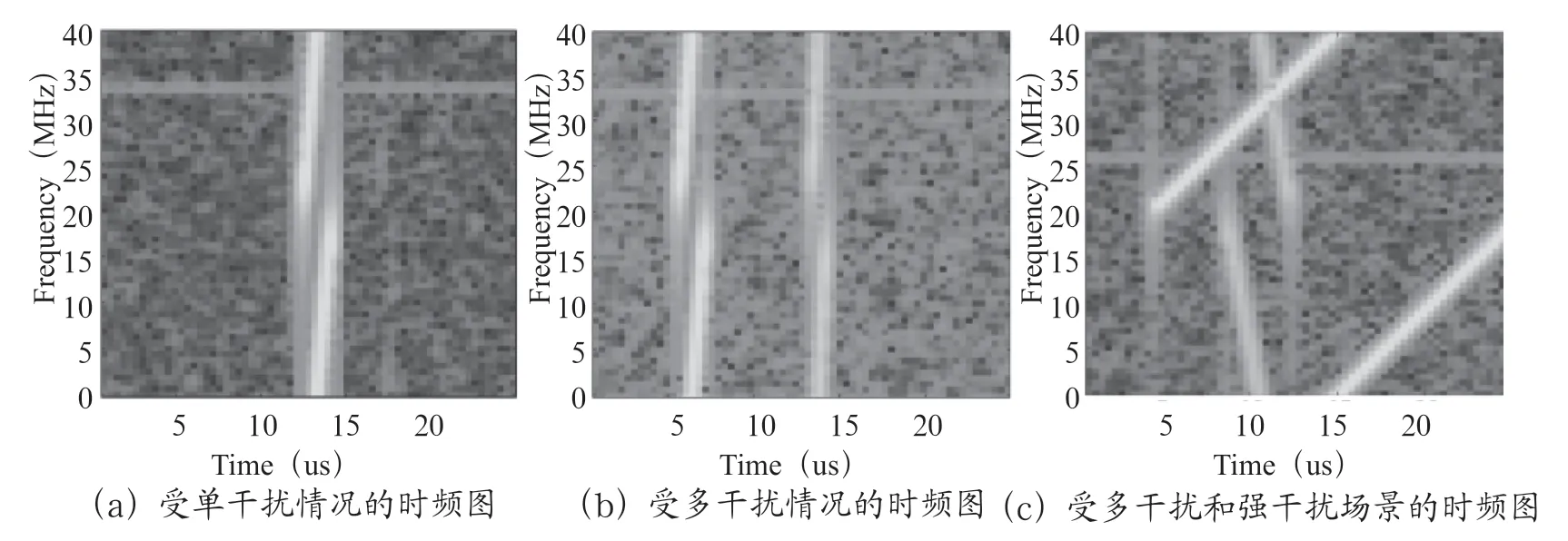
图3 受干扰的雷达信号时频图

为了解决深度学习干扰抑制模型的实测训练不足的问题，文章提出R-DCGAN 来生成毫米波雷达时频域数据，为干扰抑制模型的训练提供更加丰富多样化雷达干扰时频域数据集，以提升模型的干扰抑制性能和泛化性能。R-DCGAN模型结构如图4所示。R-DCGAN 算法基于DCGAN 重新设计了网络结构和改进模型训练损失函数，克服了GAN 和DCGAN 网络模型训练不稳定的存在的一些缺点，能够生成高质量的毫米波雷达干扰时频图。在R-DCGAN 模型开始训练之前，对少量实测数据做STFT 得到时频图，并取时频图的幅度数据作为鉴别器的真实输入数据。R-DCGAN 模型生成器利用噪声生成雷达受干扰信号时频图数据输入到鉴别器。鉴别器对输入数据做判断，辨别输入数据是生成数据还是真实数据，然后将判断结果反馈给生成器和鉴别器，更新两个模型的参数，不断反复对抗训练，使得生成器模型和鉴别器模型达到“纳什均衡”状态时完成模型训练。

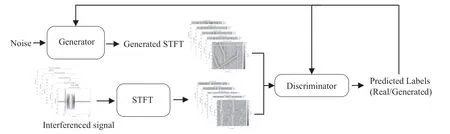
图4 R-DCGAN 模型结构

2.1.1 R-DCGAN 生成器结构

R-DCGAN 生成器网络结构如图5所示。生成器由全连接层、转置卷积层、激活层等构成。相比于DCGAN 的生成器，R-DCGAN 生成器在整体网络结构上仍然使用卷积取代池化层，但是取消了做批规范化操作的BN（Batch Normalization）层，并把所有的Relu 层换成LeakyRelu 层，输出层的激活函数选用tanh 函数。在模型的对抗训练中，把一个1×1×100 的随机正态分布噪声作为输入数据，输入后经过线性映射到大小为4×4×1 024 的张量，然后利用转置卷积对其进行上采样，最后一层转置卷积生成一个128×128×1 的时频幅度图，经过Tanh 激活函数激活后，输出一个128×128×1 的毫米波雷达时频图幅度数据。

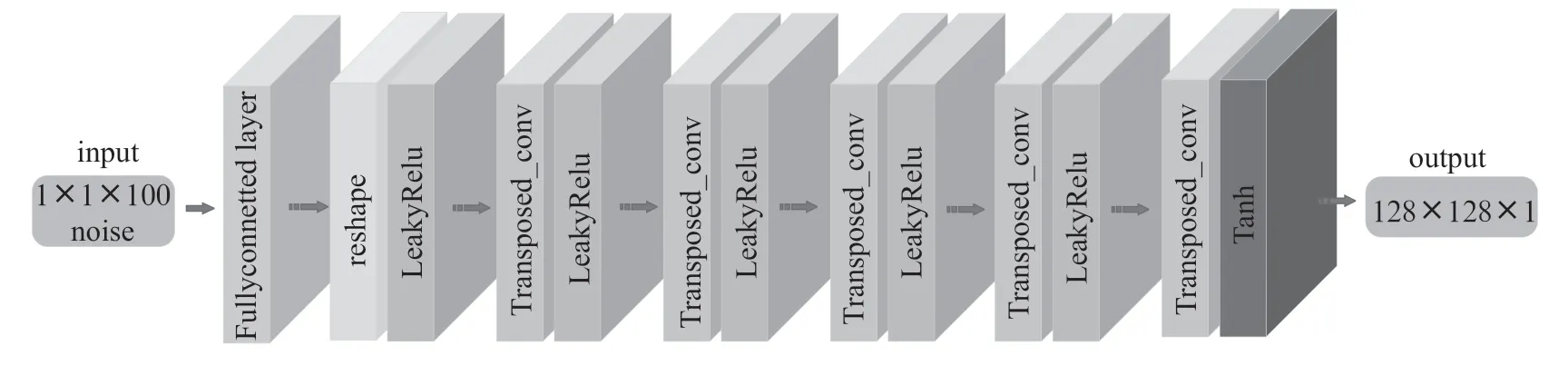
图5 R-DCGAN 生成器网络结构

2.1.2 R-DCGAN 鉴别器网络结构

R-DCGAN 鉴别器网络结构如图6所示。R-DCGAN 的鉴别器网络结构在DCGAN 鉴别器网络的基础上取消了BN层，鉴别器模型由卷积层、激活层和全连接层构成。鉴别器网络输入维度为128×128×1 的毫米波雷达时频幅度图，卷积层对其做下采样，并使用LeakyRelu 函数对每层卷积特征进行激活。最终鉴别器对来自生成器的生成的时频数据和真实数据进行真假分类，并把判别结果通过反向传播算法反馈回生成器和鉴别器，生成器和鉴别器更具反馈结果进行模型参数调整。

图6 R-DCGAN 鉴别器模型

GAN 与DCGAN 模型优化原始目标函数的任务被转变为最小化真实样本数据分布和生成样本的数据分布之间的JS（Jenson s Shannon）散度任务，而此时不管模型怎么训练，JS 散度都是一个定值，这就会造成生成器的梯度为0 而出现梯度消失的状况。在WGAN 中的Wasserstein 距离克服了梯度消失的问题，但是Wasserstein 距离不能直接用于生成对抗网络的损失函数中，需要对其增加Lipschitz 约束。而在Lipschitz 约束中，权重裁剪技术将鉴别器的所有参数值都限制在一个区间范围内，以保证在鉴别器在训练过程中所有参数都是有界的，使两个有稍微不同的样本的判别结果不会产生太大的差异。然而，在WGAN 模型的鉴别器的损失函数会最大限度地放大真实样本与生成样本之间的差异。在权重裁剪的作用下，最优的训练策略是尽可能取所有参数的极值，因此，鉴别器的参数几乎集中在区间的最大值和最小值上。

为了解决GAN 与DCGAN 模型训练不稳定的问题，同时避免WGAN 鉴别器参数不均影响生成图像质量的问题。R-DCGAN 模型选择以带梯度惩罚项的Wasserstein 距离替代原有的损失函数，既可以有效缓解训练过程中梯度不稳定现象，又避免了WGAN 中Lipschitz 约束带来的问题，提升训练过程中的稳定性。Lipschitz 限制是控制鉴别器的梯度不超过设定值，而梯度惩罚需要设置一个额外的损失项来连接梯度与之间的关系。梯度惩罚项具体操作就是在真实数据分布和生成数据分布之间做抽样处理。先随机采一对真假样本数据和一个0～1 的随机数：～，x～Px～P，～[0,1]，然后 在和x的 连线上做 随机差值采样，具体公式可以表示为：

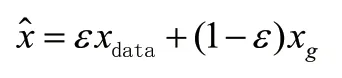
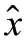
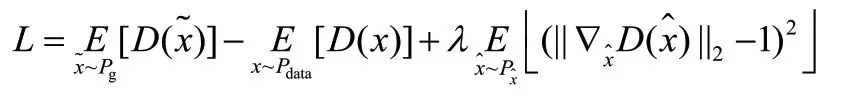
其中为权重系数。模型对每个样本独立地施加梯度惩罚，为了避免使得同一个batch 中不同样本产生相互依赖关系，所以鉴别器的模型结构中没有使用批量归一化。

本文所有的实验都是在GPU 环境下进行的，用编程语言为MATLAB，实验基于MATLAB 深度学习工具箱。具体实验环境如表1所示。

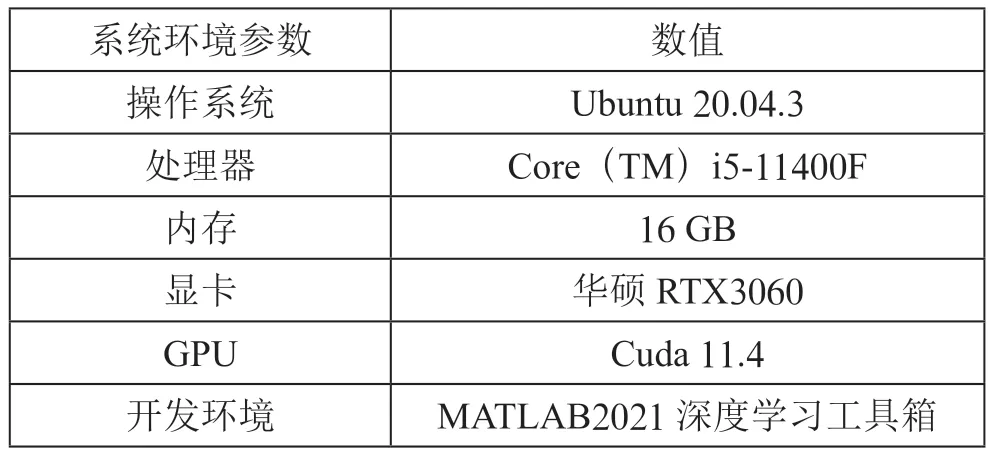
表1 实验环境配置

模型训练的具体参数配置如表2所示。为了提升各个模型生成数据的能力，训练过程中调整了模型的优化器optim、学习率lr（learningrate）、权重系数、训练次数Epoch、训练批次batchsize等参数。其他参数值使用默认设置。

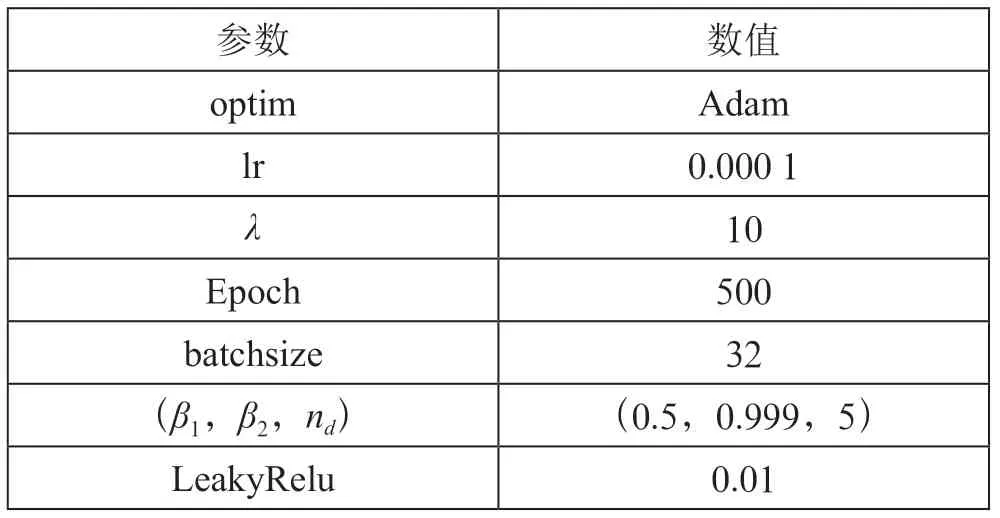
表2 模型训练参数

3.2.1 R-DCGAN 生成图像

原始干扰信号时频图像，GAN、DCGAN 和R-DCGAN生成时频图的对比图如图7所示。在GAN 生成的时频图当中，噪声和干扰的水平极高，已经完全覆盖住目标特征信息，虽然在时频图中干扰的特征突出并且呈现出多样化的情形，但是由于缺少主要的目标信号特征，对于深度学习干扰抑制模型来说，使用目标特征缺失的数据集训练出来的模型，性能会有所降低。由前文对DCGAN 的分析可知，DCGAN并没有对GAN 的损失函数做出改进，导致其模型仍然存在训练不稳定或者生成图像单一的问题。DCGAN 模型生成的图像，目标信号特征单一重复，干扰信号特征虽然具有多样性，但因其特征太不明显，同样会影响深度学习模型在训练过程中对于多种复杂干扰场景的学习，进而降低模型的干扰抑制性能。而对于文章提出的R-DCGAN 模型生成的雷达时频图，从生成图像的目标特征和干扰特征的显著程度看，两种主要的特征都十分明显，生成图像的具有多样性，无论是干扰特征还是目标特征，都能够满足毫米波雷达信号的随机性与复杂性的要求，R-DCGAN 生成的时频图数据的整体噪声水平接近真实图像。

图7 不同模型生成时频图对比

3.2.2 R-DCGAN 生成样本对CNN 干扰抑制模型性能影响实验

为了客观评价三种模型生成的毫米波雷达时频图数据集对CNN 干扰抑制模型性能的影响。使用模型生成数据和仿真数据混合，训练CNN 干扰抑制回归模型来抑制毫米雷达干扰，用训练出来的模型干扰抑制能力来评价生成数据的质量。本节设置了4 组对比实验，具体实验设置为：

（1）用20 000 个仿真数据训练CNN 干扰抑制模型1。

（2）用10 000 个GAN 生成数据与10 000 个仿真数据混合训练CNN 干扰抑制模型2。

（3）用10 000 个DCGAN 生成数据与10 000 个仿真数据集混合训练CNN 干扰抑制模型3。

（4）用10 000 个R-DCGAN 生成数据与10 000 个仿真数据集混合训练CNN 干扰抑制模型4。

4 组模型训练过程中，80%数据集作为训练数据集，20%作为验证集。CNN 干扰抑制模型训练过程的参数设置如表3所示。采用Adam 优化器对模型进行优化，模型训练迭代次数设置为5 000 次，其中MaxEpochs 设置为10，训练数据对网络进行10 轮训练，每轮训练500 次。MiniBatchSize 设置为32，网络模型一次查看32 个训练数据。初始学习率设置为0.000 01，每经过一定数量的轮次训练时，按指定的因子降低学习率，学习率下降因子设置为0.9。

表3 CNN 干扰抑制模型训练参数

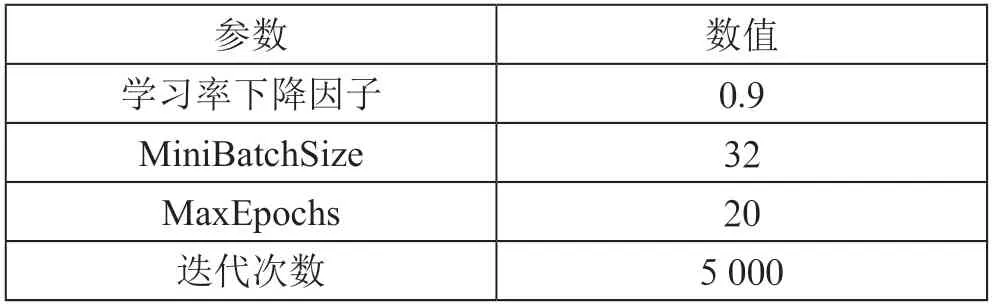
续表

CNN 回归网络模型使用均方根误差（Root Mean Square Error,RMSE）作为损失函数，RMSE 用来衡量观测变量和真实变量之间的偏差程度。CNN 回归模型的损失函数可以表示为：

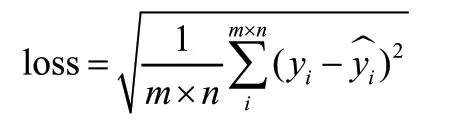
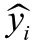
CNN 干扰抑制模型训练时的RMSE 变化情况如图8所示。模型1 收敛时最终RMSE 为35.4，模型2 为37.5，模型3 为33.8，模型4 为32.8，从模型的RMSE 情况对比，模型2 使用GAN 生成数据进行混合，由于数据噪声过大，并没有提升模型性能。模型3 使用DCGAN 生成数据进行混合训练，模型RMSE 比仿真数据略微有所提升，但其提升效果没有模型4使用R-DCGAN生成数据训练的模型效果好。

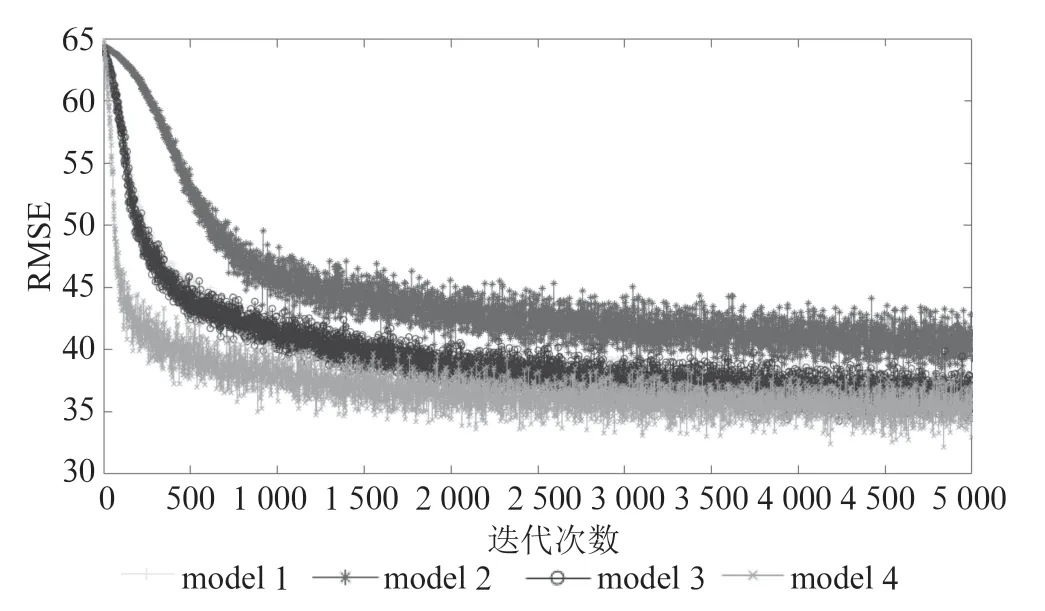
图8 4 个模型的训练RMSE 对比

采用仿真毫米波雷达干扰数据与实测干扰数据验证模型的干扰抑制能力，选用雷达目标信标信噪比作为评价模型干扰抑制性能的指标。目标信号信噪比的公式可以表示为：

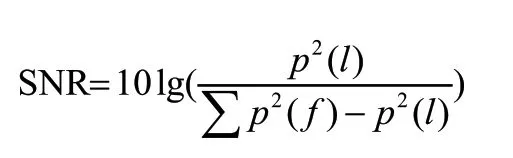
其中，（）代表目标信号的频谱峰值能量，∑（）代表信号频谱的总能量。目标信号信噪比越高，说明目标信号强度越强，则说明信号越好，目标信号更加容易被检测到。

（1）CNN 模型抑制仿真雷达干扰。模型抑制仿真信号时频域干扰效果对比如图9所示，（a）图表示原始的受干扰信号的时频图。（b）（c）（d）（e）分别表示模型1、模型2、模型3、模型4 的抑制干扰效果。对比原始的干扰时频图，可以明显看出时频图当中的干扰特征已经被抑制，同时目标特征得到加强，但是对于前三个模型的抑制干扰时频图，在抑制干扰的同时也影响到目标信号的特征，在干扰与目标交界处，有明显的信号缺失。但是在模型4 中，信号丢失情况并不严重，干扰抑制性能优于其他3 个模型。

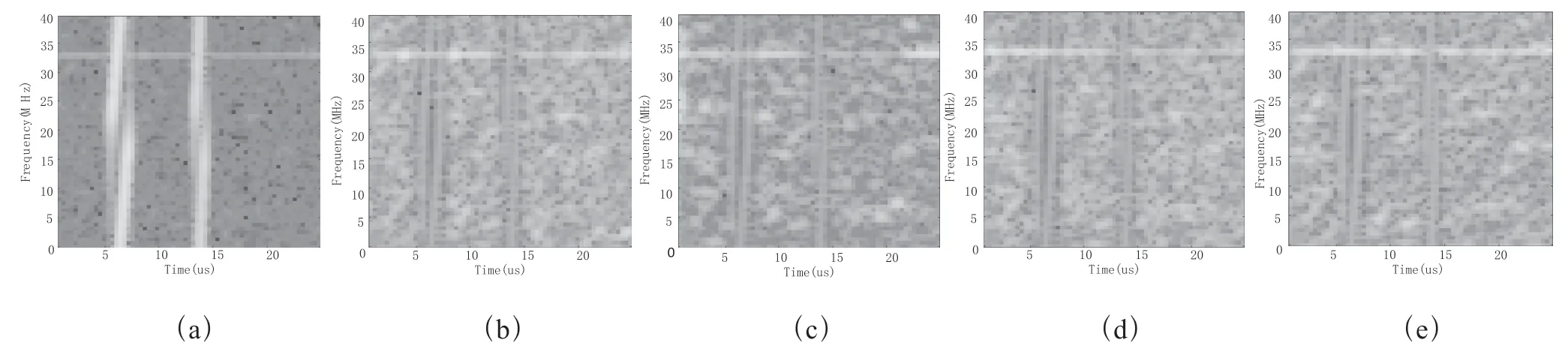
图9 CNN 模型抑制仿真信号时频域干扰效果对比

为了更加全面的评价用不同数据集训练出来的雷达干扰抑制模型的性能，用4 个模型分别对2 000 个仿真干扰信号进行干扰抑制，然后取平均信噪比作为评价指标。具体实验结果如表4所示。2 000 个干扰信号目标信号平均信噪比为-21.01 dB，而干净信号的信噪比是-4.58 dB，模型1 抑制干扰信号后，目标信噪比为-5.02 dB，相比于受干扰信号的信噪比提高了15.99 dB。对于模型2，由于GAN 生成的数据噪声水平太高，目标特征不明显，抑制干扰后的目标信噪比为-5.60 dB。对于DCGAN 和R-DCGAN，模型3和模型4 对于干扰的抑制效果提升更明显，分别是-3.61 dB和-2.17 dB。相比于受干扰信号，信噪比提高了17.40 dB和18.84 dB。从模型对于目标信噪比的提升效果来看，R-DCGAN 生成数据与仿真数据混合训练出来的干扰抑制模型性能最好。

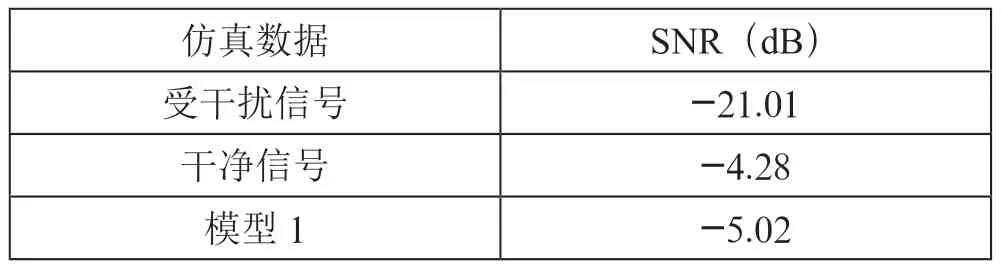
表4 模型抑制仿真干扰性能对比

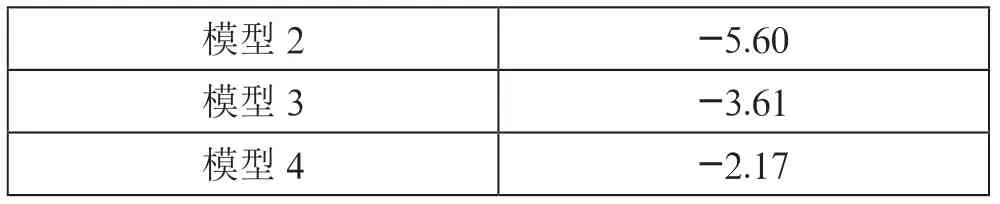
模型2 -5.60模型3 -3.61模型4 -2.17

（2）CNN 模型抑制实测雷达干扰。实测干扰信号抑制效果如图10所示，4 组模型都能够较大程度的抑制干扰信号，对于模型1、模型2 和模型3 的干扰抑制效果中，目标特征丢失比较严重。而对于模型4，目标的特征丢失就不那么明显，模型4 的干扰抑制性能相比于其他3 个模型有所提升。

图10 CNN 模型抑制实测信号时频域干扰效果对比

CNN 模型抑制实测干扰性能如表5所示，实测雷达信号有两个目标，取两个目标的平均信噪比作为模型干扰抑制性能对比。从平均水平看，模型1 抑制干扰信号后，各个模型对于受干扰信号信噪比的提升情况分别为，模型1 提升22.63 dB，模型2 提升19.11 dB，模型3 提升22.64 dB，模型4 提升23.35 dB。从实测信号中两个目标平均信噪比的提升水平来看，模型4 的干扰抑制性能会优于其他三个模型，模型对于实测数据具有较强的泛化性能。

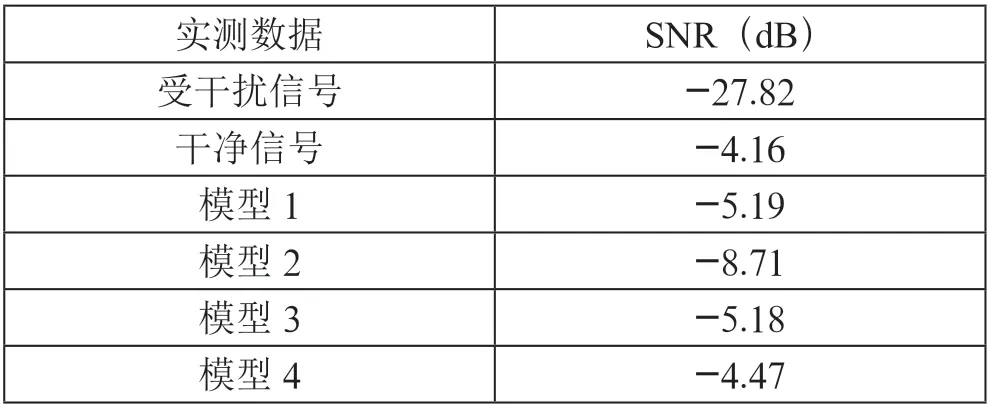
表5 模型抑制实测干扰性能对比

为了解决在训练深度学习模型抑制时频域干扰时实测数据量不足的问题。文章提出R-DCGAN 模型来生成毫米波雷达时频图数据。区别于GAN 与DCGAN 模型，R-DCGAN模型保留了DCGAN 的优势，融合了CNN 的特征提取能力和GAN 的图像生成能力，同时使用带梯度惩罚的Wasserstein 距离作为新的目标函数，以克服原始生成模型训练不稳定，生成数据单一、质量差的缺点。带梯度惩罚的Wasserstein 距离解决了原始损失函数中JS 散度会造成训练过程中梯度消失的问题，同时又避免了WGAN 中Lipschitz约束带来的鉴别器模型参数分布不均问题，能够进一步提升训练过程中的稳定性。实验结果表明，对比与GAN 与DCGAN 模型生成的数据，把R-DCGAN 模型生成的雷达信号时频图样本应用在CNN 干扰抑制模型训练中，能够更有效提升CNN 模型的干扰抑制性能。