基于尾流效应和分组补偿的风电场功率优化

李啸吟，王湘明

（1.沈阳工业大学 人工智能学院，辽宁 沈阳 110870；2.沈阳工业大学 信息科学与工程学院，辽宁 沈阳 110870）

近年来，随着风电技术发展，风电场规模和风电机组的容量不断增大，导致风电场输出功率波动变大尾流效应影响增强。如何在确保风电场输出功率稳定的前提下，尽可能地减少动作频率成为研究热点之一。

文献[2]根据尾流模型提出了一种基于粒子群优化算法的偏航控制方案，使尾流偏离下游风电机组风轮面来最大化风电场的输出功率，该方法将风电场的发电量提高了15%～20%。该方法证明，减弱尾流影响确实能够增加风电场的发电量。但该文献单纯控制风电机组的偏航，未考虑变桨和转速对风电场发电量和输出功率稳定性的影响。

文献[3]提出一种改进的分形插值-神经网络预测（FINN）算法，并将其应用在了时域超前变桨控制中，该方法能够从转速和输出功率两个方面对风电机组的变桨控制进行改进，从而体改风电机组的运行稳定性。但其只在风电机组中进行了验证，没有将变桨控制应用在风电场的控制中。

文献[4]为了降低尾流效应对风电场的输出功率和载荷的影响，提出了一种兼顾尾流效应和风电机组载荷的风电场优化控制模型。将混合蛙跳改进策略加入到鲸鱼优化算法，通过控制轴向诱导因子使风电场达到最大输出功率和最小载荷。文献[5]针对传统控制方法难以有效抑制风电场功率波动的问题，提出了集群预测协调控制。文献[4]对风电机组直接进行控制，最求风电机组的控制最优，会导致风电场中风电机组的误差叠加，并且未考虑风电机组之间的相互误差补偿。文献[5]以超短期风电功率预测为前提，以当前风电机组状态进行集群，未考虑风电机组之间的尾流影响及其相互联系。

因此，本文探索一种通过尾流效应将风电场中的风电机组联系起来的控制方式，并通过分组补偿控制降低风电机组的动作次数。通过前排风电机组的尾流效应计算后方风电机组的来流风速，并根据前排风电机组的误差调节后排风电机组的给定输出功率，从而降低整个风电场输出功率的偏差和动作次数。

风电机组的输出功率为：

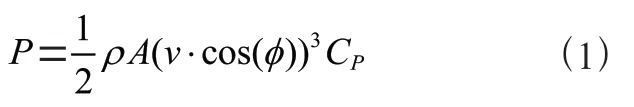
式中，为空气密度；为风轮面积；为风速；为风轮面与风速方向的夹角；C为风能利用系数，其为叶尖速比和桨距角的函数，并有：

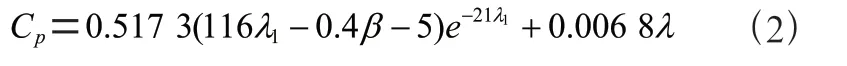
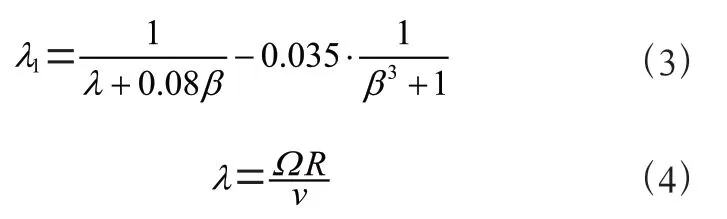
式中，为风轮旋转角速度；为风轮半径。并且有风能利用系数与轴向诱导因子的关系：

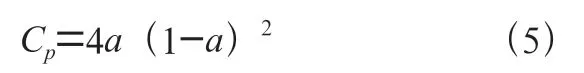
其中，和C如下关系：（1）相同下，C有且仅有一个极值同样也是最大值，对应的最佳叶尖速比为，＜时，C随的增大而增大，＜时，C随的增大而减小。（2）不同下，C的最大值不同，并且最大C所对应的最佳叶尖速比也不同。

风能利用系数C与轴向诱导因子是一一对应的，并由Betz 极限可知＜0.5，再结合式（2）、式（4）和式（5），可根据桨距角和风轮旋转角速度计算出轴向诱导因子。

风流过风轮会在后方形成尾流区域，尾流区域内的风速受到不同程度的影响，从而影响其中的风电机组，导致风电场中风电机组的控制产生连锁反应。风电场中的尾流效应如图1所示。

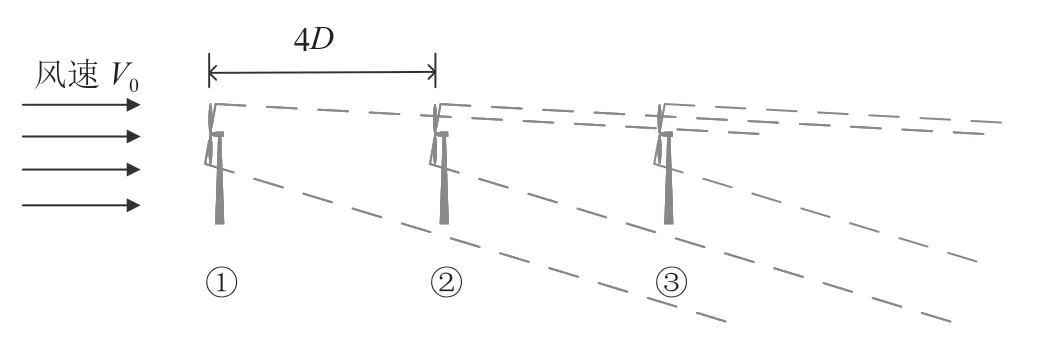
图1 尾流效应影响区域

图1风电场中各风电机组的相对位置固定，为了方便研究，对每个风电机组进行如图所示的编号。图1中所绘制的是偏航为10°时的尾流区域。

Jensen 尾流模型是较为经典的尾流模型，因其形式简单、编码容易、计算效率高且精度较高而得到广泛的应用，其一般形式为：

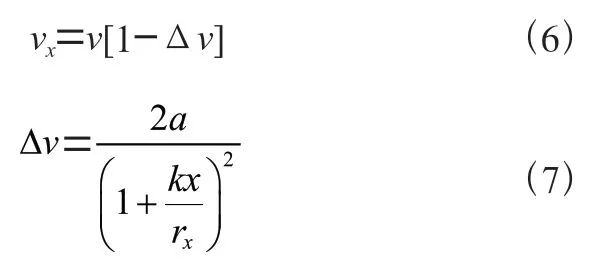
式中，为风电机组来流风速；v为风电机组正后方距离处的风速；Δ为风速损失占比；为轴向诱导因子；为尾流的膨胀系数，陆地上=0.075；r为风电机组正后方距离处的尾流半径，其中为风轮后方近距离处的尾流半径：

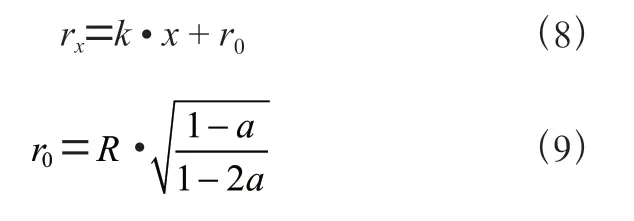
根据以上分析及上节所述，可以推导出风电机组风能利用系数C与尾流区域风速v之间的关系。当风电机组轮毂风速为定值时：（1）距离相同时，风能利用系数从0.2 阶梯增加到0.45，的过程中尾流风速不断减小，且减小幅度不断变大；（2）风能利用系数不变时，随着距离的增加，风速不断增加，且增长幅度不断减小。

当多个风电机组的尾流区域重叠时会产生尾流的叠加效应，能量守恒模型能够给出较为准确的尾流叠加效果：

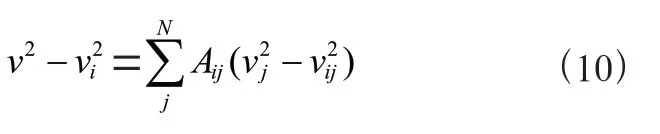
式中，v为第台风电机组轮毂处的风速；为尾流叠加风电机组的总数；v为第台风电机组轮毂处的风速；v为第台风电机组只受第台风电机组尾流影响时的轮毂处风速；A为：

式中，S是第台风电机组受第台风电机组尾流影响的风轮面积。

根据风电机组在尾流区域的位置，和受到尾流影响的强度对风电机组进行分组。将最先迎风不受尾流影响的风电机组记为A 组，其后最先受到尾流影响的风电机组记为B 组，在B 组风电机组尾流区域的风电机组记为C 组。假设风电场中风电机组之间的相对位置固定，则当自然风从某一方向流入风电场，根据尾流模型即可计算各风电机组之间的尾流关系以及前排风电机组功率调节对后排风电机组的影响，也可以通过调节后排风电机组的输出功率，补偿前排风电机组的偏差。

风电场风速为，方向为v，因为组风电机组不受尾流影响，则A 组的轮毂风速为v=，风向v=v。首先不对A 组风电机组进行控制，以当前状态计算A 组风电机组的实际输出功率P，及其与给定功率的偏差，即：

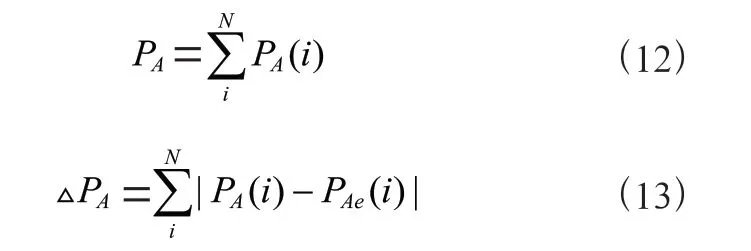
式中，是A 组中第台风电机组，是A 组风电机组的数量。由P（）可以计算出风能利用系数C，进一步可以计算出尾流区域的半径和风速，以及对B 组和C 组的影响。

风电场的控制流程如图2所示。

（1）由风电场的来流风速和尾流效应，计算A 组、B 组和C 组所包含的风电机组，以及各组的最大输出功率P、P和P，根据各自最大输出功率粗略估计风电场的总输出功率，并根据电网需求功率对A 组、B组和C 组进行功率分配P、P和P。

（2）计算A 组风电机组的功率和偏差，A 组的控制流程如图2中A 组虚线框所示。若A 组偏差小于0.1 倍的P，则A 组的桨距角、偏航和风轮转速保持不变；若A 组偏差大于0.1 倍的P，则首先对A 组进行桨距角和风轮转速的调节，使A 组风电机组的输出功率偏差减小，若偏差仍然大于0.1 倍的P，则通过偏航调节输出功率。

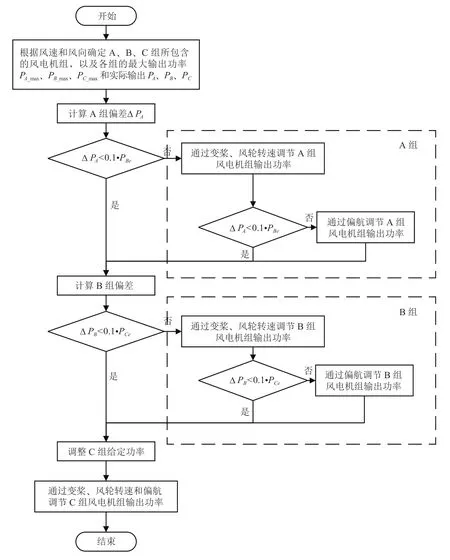
图2 基于尾流效应和分组补偿的风电场控制流程图

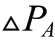
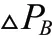
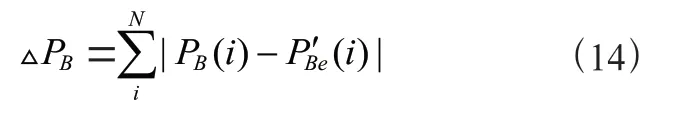
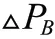
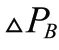
A、B 组风电机组控制偏航将导致尾流区域变化，从而使分组的风电机组发生改变，因此优先对桨距角和风轮转速控制。C 组是后排风电机组其尾流区域不会影响其他风电机组，因此，可以对C 组的桨距角、风轮转速和偏航进行调整，使其偏差满足输出要求。偏差计算方式如公式（15）所示：

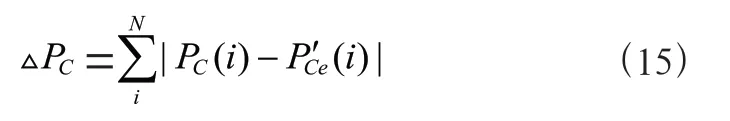
为了验证控制策略的有效性，本文使用Matlab/Simulink对直驱永磁同步风力发电机组进行仿真，考虑到控制的类似性，采用3 台风电机组1、2 和3 分别代表A 组、B 组和C组风电机组，风电机组的前后间距为4D，如图1所示。风电机组相关参数为：额定风速13.5m/s，风轮半径56 m，空气密度1.335 kg/m，风电机组额定功率5 MW，桨距角调节范围0～25°，偏航调节范围为0～40°。

对风电场来流风速进行模拟，如图3a 所示。基本风在0～10 s 为3 m/s，10～20 s 风速逐渐攀升到13.5 m/s，20～80 s保持13.5 m/s不变，为了模拟风电场中风速的复杂性，25～40 s 加入最大值为1 m/s 的阵风，60～75 s 加入最大值为1 m/s 渐变风，以及始终存在的最大值为1 m/s 的随机风。

图3b 为基于尾流效应和分组补偿策略控制下各风电机组的轮毂风速，图3c 为单台最优控制策略下各风电机组的轮毂风速。

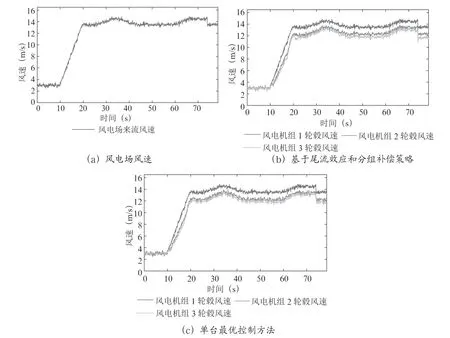
图3 风电场来流风速及各风电机组的轮毂风速

从图3可以看出，在风电场来流风速相同时，基于尾流效应和分组补偿策略的风电机组轮毂风速差值变化较为明显，表明前后排风电机组相互之间存在调节关系，而单台最优控制策略的风电机组轮毂风速差值变化较小。

假设电网需求功率为12.4 MW。图4为基于尾流效应和分组补偿的控制策略风电机组1、2 和3 的输出功率、桨距角、偏航和风轮转速曲线；图5为单台最优控制策略风电机组1、2 和3 的输出功率、桨距角、偏航和风轮转速曲线。

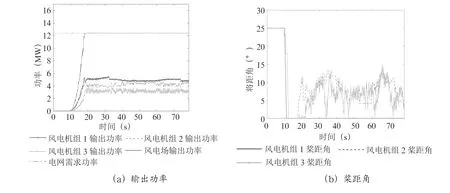
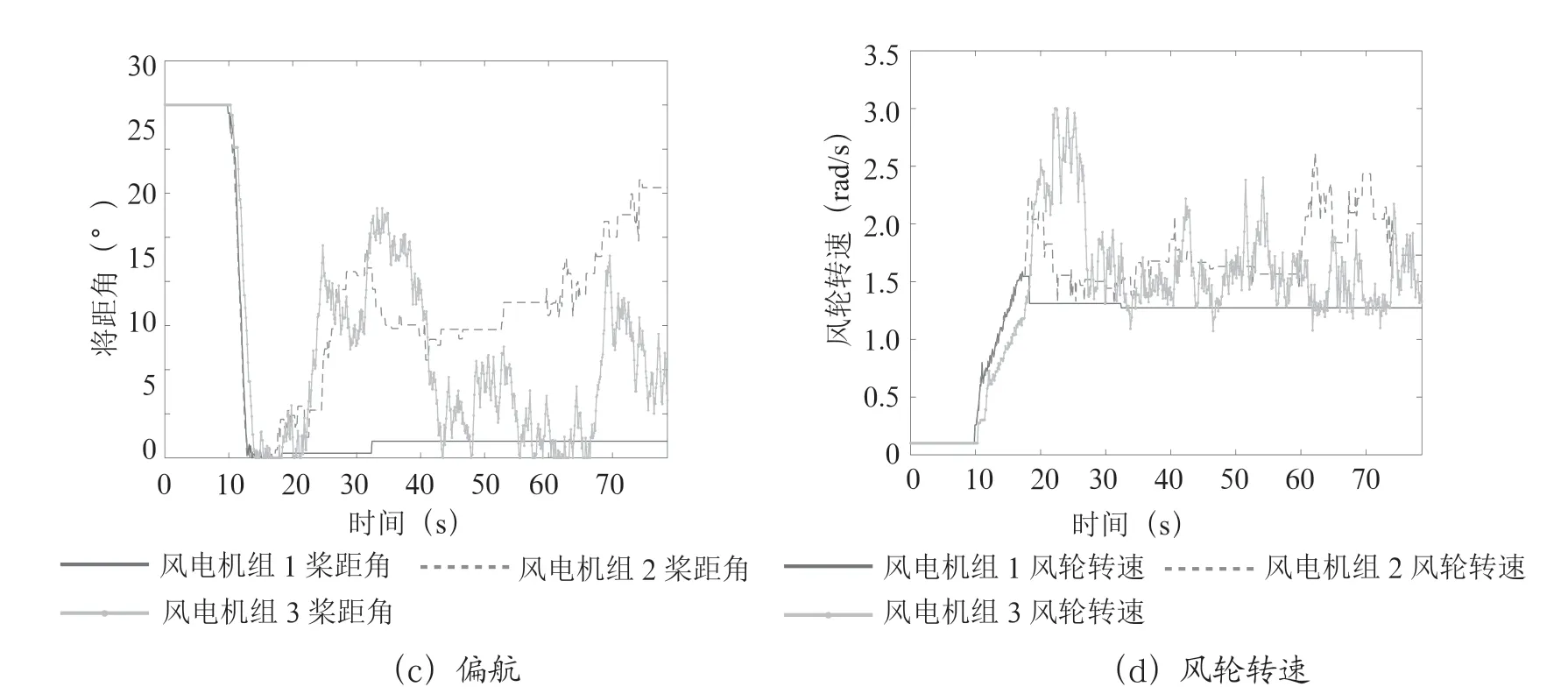
图4 基于尾流效应和分组补偿控制策略的输出功率曲线和控制量曲线

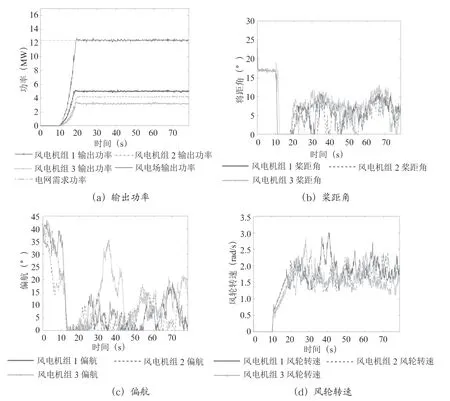
图5 单台最优控制策略的输出功率曲线和控制量曲线

从图4和图5可以看出，在2 种控制策略下，基于尾流效应和分组补偿的控制策略能在保证输出功率不超过限制的情况下，减少风电机组桨距角、偏航和风轮转速的动作次数，特别是风电机组1 和2 的动作次数降低的更为明显。相对于单台最优控制策略，基于尾流效应和分组补偿的控制策略风电场输出功率波动幅度明显变小、稳定性增加。

仿真实验结果表明，与单台最优控制策略相比，本文提出的基于尾流效应和分组补偿的控制策略减少了前排风电机组桨距角、偏航和风轮转速的变化次数，降低了对变桨和偏航结构的载荷，避免了对机组传动链的部分冲击，提高了风电场输出功率的稳定性和控制精度。