基于改进灰色马尔可夫模型的雷达备件需求预测

蔡志成，王昫

（中国人民解放军空军预警学院 雷达士官学校，湖北 武汉 430345）

在雷达装备保障中，备件直接影响着雷达装备持续作战能力。备件不足会导致雷达装备战备完好性下降、影响部队战斗力，而备件储备过量既增加保障难度也浪费保障经费。因此，准确预测备件需求对于保持雷达可用性、维持合理备件库存具有重要意义。

备件需求的预测方法主要有四大类：实战统计法、解析分析法、经验系数法和模拟仿真法等。本文采用解析分析法，通过分析备件消耗量历史数据，建立改进灰色马尔可夫组合模型来预测下一阶段备件需求。灰色系统理论的GM（1，1）预测模型能够弱化备件消耗序列的随机性，发掘出样本数据发展趋势，然而该模型对不规则变化和波动较大的数据预测精度较低。马尔可夫链预测模型可以对波动性较大的数据进行研究，将灰色预测理论与马尔可夫链相结合，能够实现两者优势互补。

本文针对装备备件消耗量变化随机性较强特点，提出一种改进的灰色马尔可夫模型计算备件需求量的预测方法，即通过对备件历史消耗数据进行分析，运用改进后的模型求需求量的预测值。首先用标准灰色预测GM（1，1）模型求出消耗量的灰色预测值，然后运用马尔可夫理论，对预测值和实际值两者的误差进行状态划分，得出马尔可夫链预测模型，求出转移概率矩阵；改进利用固定的初始状态和转移概率矩阵对未来状态的预测方法，采用5 个与待测阶段最近的状态数据最为初始状态，共同预测待测阶段的状态概率向量并确定状态区间，利用模型的预测值更新选定的5 个初始状态，进行后续阶段预测，实现对灰色预测值进行修正、提升模型预测精确度的目标。

灰色预测模型是一种用灰色系统进行预测的方法模型，通过关联分析，对原始数据进行生成处理来寻找系统变动的规律，生成有较强规律性的数据序列，然后建立相应的微分方程模型来进行预测。

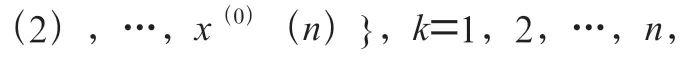
（）的紧临均值生成序列：

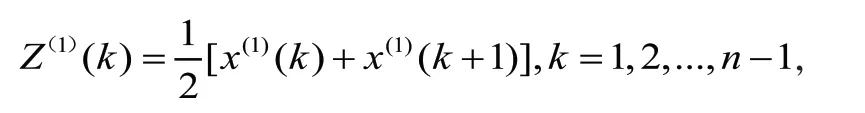
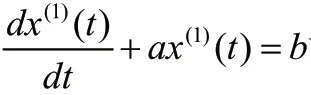
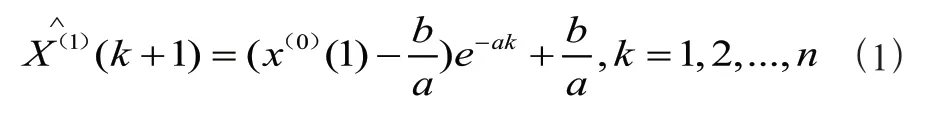
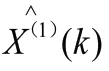
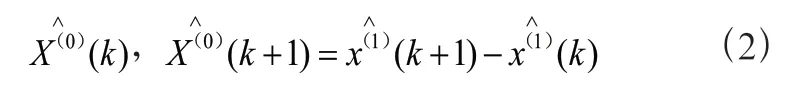
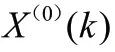
灰色预测模型GM（1，1）模型的精度检验：相对误差、关联度和后验差检验。

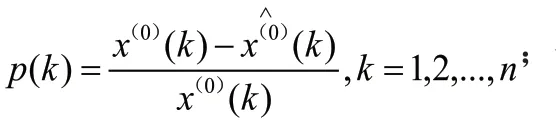
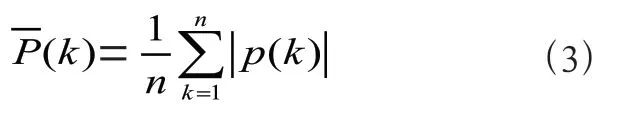
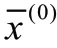
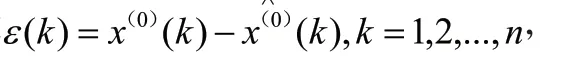
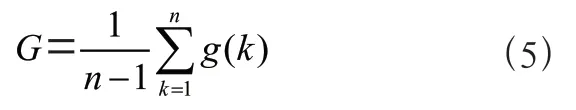
计算小误差概率：

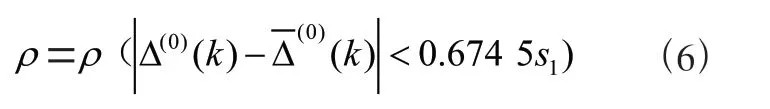
GM（1，1）模型精度检验主要将上述计算参数模型预设的误差范围（详见表1）进行比较。

表1 灰色模型精度验证表检验精度等级对比表

马尔可夫预测模型是一种用于预测事件的发生概率的方法，其根据事件当前的状况来预测未来各个时刻状态变动情况。模型最关键的环节就是对研究的数据进行合理的划分。不同的划分方法会直接影响到状态转移概率矩阵，预测结果会相差很大。本文利用灰色预测模型的残差来划分状态空间。

将残差序列 划分为个状态，任一状态区间为：E=（，），=1，2，…，，，）分别为状态E的上、下限，其状态集合为E=（，，…，E）。残差的状态划分通常以样本数和预测误差范围为基础，可将状态划分为3 至5 个。

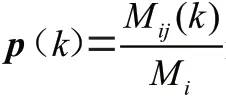
随机事件的步状态转移概率矩阵可表示为：

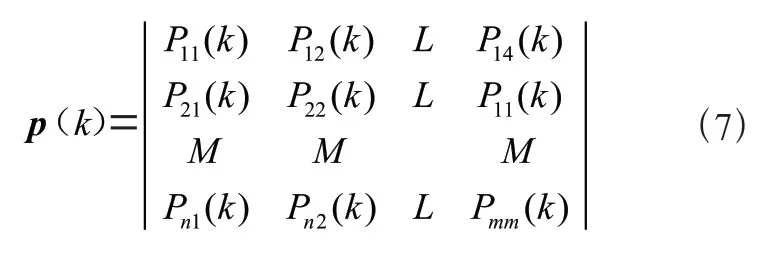
通常求得了一步状态转移概率矩阵，即可预测出待测对象下一步的状态转移情况。若为稳定性系统，则步状态转移概率可表示为：

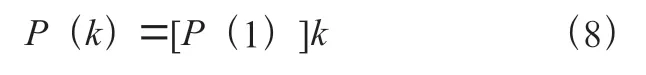
根据上式，只要知道转移概率矩阵、初始状态概率向量，就可以求得系统在任意时刻的的状态概率向量。假设预测对象处于E状态，此时的初始状态概率向量是已知的，需要预测+1 时刻的状态，则只需观察状态转移概率矩阵中第行的转移概率，如果第列为第行中概率的最大值，那么预测对象下一阶段极有可能从状态E变为状态E。

由于任何样本都存在局限性，在实际的需求预测中，通过状态存在的频率计算出的状态转移概率矩阵是不稳定的。为降低多步预测产生的误差，笔者采用多个预测的状态概率累加取最大值的方法求待测时刻的最可能状态，选取与待测阶段最近的前连续5 个阶段的已知状态，分别用相应的k 步状态转移概率矩阵求得待测的状态概率向量组成概率矩阵，将多个状态对应概率进行累加，以最大概率准则确定待测阶段的最可能状态。后续则将该预测出的状态作为已知，并以此状态为基础进行进一步的测。具体步骤如下：

设预测对象在1 至（＞5）阶段状态为，，…，E，为求+1 阶段的状态，利用第E、E、E、E、E五个阶段状态的初始概率向量，分别结合一步至五步状态转移概率矩阵，得出+1 阶段的状态概率矩阵P，其包含5 个概率向量：

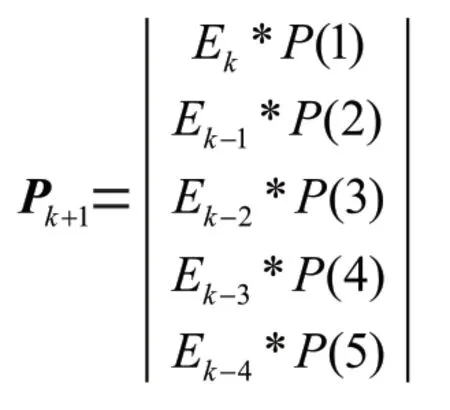
分别计算P概每一列的概率和，取概率和最大值所对应的状态为阶段+1 的状态。后续阶段（如P）状态的预计，将预测到的+1 阶段状态作为已知，所需的五个阶段状态中加入阶段+1 状态，剔除最早的一个阶段状态，以此循环迭代预测后续阶段的状态序列。

改进后的灰色马尔可夫模型预测值的与其残差所处的状态有关，一般取状态区间中点作为修正值的计算依据，设预测对象下一步转移到E状态，则改进后的灰色马尔可夫模型预测值为：

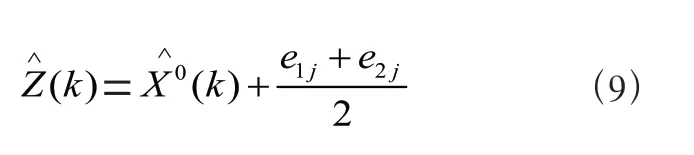
以某单位某典型雷达备件Q 的月度统计的消耗量为例，表2为2019年1月至2020年3月连续15 个月备件Q 的消耗量。为便于进行模型的计算和验证，笔者将该15 个月消耗数据看作连续时间序列，前10 个作为样本数据，后5 个数据作为检验数据，采用改进灰色马尔可夫模型对样本数据进行拟合和预测，检验模型的精确度及可用性。

表2 某型雷达备件Q 消耗的时间序列

根据备件消耗量的前10 个数据，经级比检验，该样本数据可以利用灰色模型进行预测。采用灰色预测模型，得出模型的预测值，并计算相应的绝对误差、相对误差，并同步进行模型的精度检验指标值计算。相关数据如表3所示。

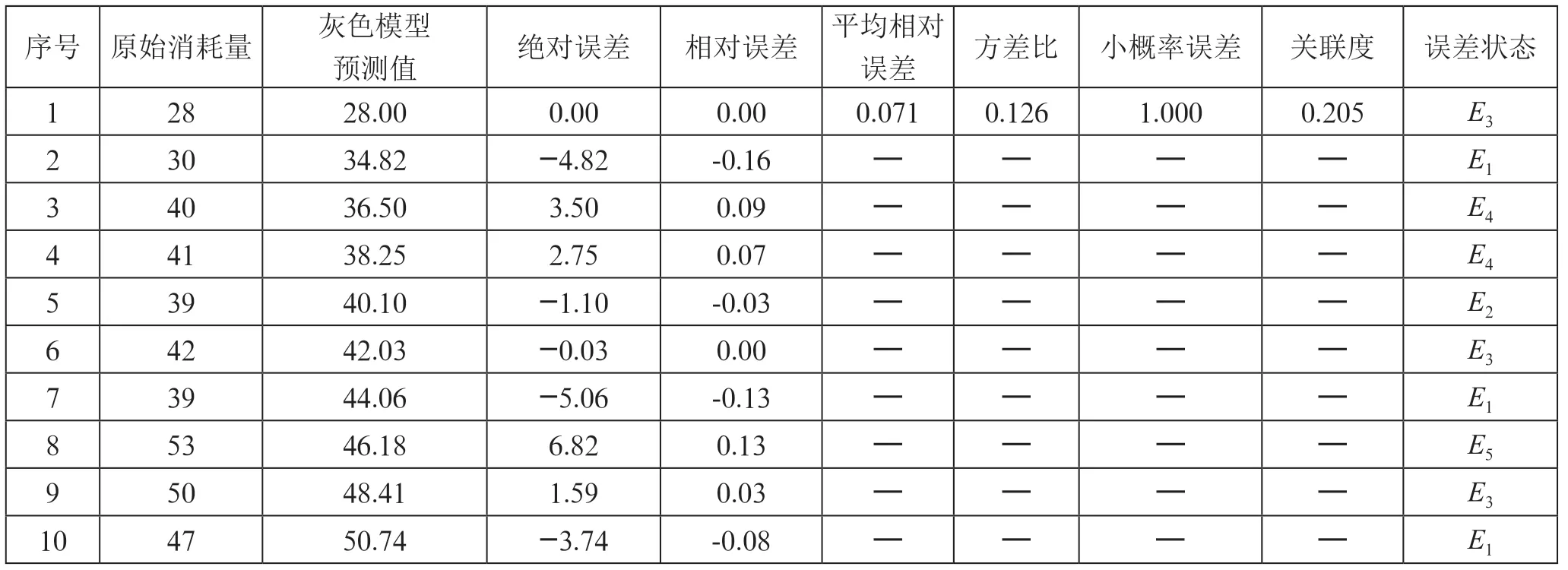
表3 灰色预测模型预测结论

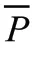
采用等距划分，将绝对残差序列划分5 个状态[-5.056，-2.681）、[-2.681，-0.306）、[-0.306，2.070）、[2.070，4.445）、[4.445，6.820]，详情见表2。结合划分的绝对误差状态序列，求出1 至5 步的状态转移概率矩阵：P（1）、P（2）、P（3）、P（4）、P（5）。

根据改进的灰色马尔可夫模型，求出第11 至15 阶段的预测值，并计算出模型精度检验指标值，具体如表4所示。

根据表4计算结果，在序号为11 至15 阶段的消耗量预测中，灰色模型的预测值与实际消耗量误差分别为2.817、0.254、-4.433、-4.249、-8.201，模型预测的精度指标平均相对误差为0.107、方差比为0.185、小误差概率为1、关联度为-0.951，预测精度较低。

表4 检验数据部分——灰色模型与改进灰色马尔可夫模型预测数据对比

改进灰色马尔可夫模型预测值与实际消耗量误差分别为-0.441、1.935、4.686、0.559、-0.441，模型预测的精度指标平均相对误差为0.044、方差比为0.092、小误差概率为1、关联度为0.710，模型的预测精度较高。由此可见，改进的灰色马尔可夫模型在该备件需求预测方面具有明显优势。

灰色马尔可夫预测模型通过将随机的时间序列分解成为灰色模型预测的趋势变动序列和马尔可夫模型预测的随机变动序列，利用马尔可夫模型的预测状态对灰色模型预测值进行修正，能较好的发挥出灰色预测和马尔可夫预测各自的优势，提高综合预测精度。文中改进的灰色马尔可夫预测模型优化了初始状态的选取和待测状态的确定方法，利用多初始状态、多步计算取最大概率确定状态的思路，进一步提高了模型预测的精度。然而，马尔可夫模型的预测核心是状态转移概率矩阵的确定，在雷达备件预测中，实际备件需求与外界环境、任务形势变化有较大影响，历史样本数据的具有较大的局限性，由此得出转移概率矩阵在多步预测后精确度下降较快，如何能够根据状态的实际变化动态更新马尔可夫模型的状态转移概率矩阵，是接下来的研究重点。