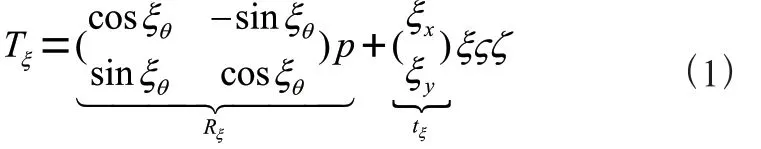摘 要:文章以生鲜产品配送为背景,分析了近年来生鲜产品配送和带时间窗车辆路径问题相关文献,基于带时间窗车辆路径问题构建了最小化车辆行驶成本的数学模型,并使用CPLEX求解器中的分支定界算法求解。将求解结果与已知最优解和其他文献比较表明,分支定界算法在求解带时间窗车辆路径的生鲜产品配送问题时具有可行性和优越性。
关键词:交通工程;带时间窗车辆路径问题;生鲜产品;CPLEX;分支定界算法
中图分类号:TP18 文献标识码:A 文章编号:2096-4706(2020)24-0110-04
Research on Vehicle Routing Problem with Time Window in Fresh Product Distribution
LI Jun
(School of Business Administration,Chongqing Technology and Business University,Chongqing 400067,China)
Abstract:Based on the background of fresh products distribution,this paper analyzes the literature on fresh product distribution and vehicle routing problem with time windows in recent years. Based on the vehicle routing problem with time windows,a mathematical model to minimize the vehicle driving cost is constructed and solved by the branch and bound algorithm in CPLEX solver. Compared with the known optimal solution and other literatures,the results show that the branch and bound algorithm is feasible and superior in solving the fresh product distribution problem with time window vehicle routing.
Keywords:traffic engineering;vehicle routing problem with time window;fresh product;CPLEX;branch and bound algorithms
0 引 言
生鲜产品配送具有温度和新鲜度等限制,产品的配送效率直接影响产品质量,从而影响消费者满意度。此外由于配送不及时导致的产品损耗直接影响企业成本。本文在生鲜产品配送的带时间窗车辆路径问题(Vehicle Routing Problem with Time Windows,VRPTW)[1]的研究课题中,发现将生鲜产品在合适的时间内配送给客户至关重要。目前大部分研究使用启发式算法求解大规模算例,容易陷入局部最优,且忽略了生鲜产品小批量、多批次等特点[2]。故有本篇研究,使用精确算法求解小规模算例,为的是提高生鲜配送效率、降低生鲜配送成本,为推动生鲜配送行业发展做出贡献。
VRPTW最早由Savelsbergh提出,是在车辆路径问题的基础上增加了顾客接受配送服务的时间窗要求,较VRP更贴近实际生活。VRPTW已被证实是NP-hard问题,主要由启发式算法或精确算法求解。当问题规模较大时,启发式算法较易得到满意解。叶勇等[3]以城市物流配送和交通运输中的VRPTW为背景,以总运输成本最小为目标,使用狼群算法求解。当问题规模较小时,精确算法较易得到最优解,但目前国内使用精确算法求解车辆路径问题的文献较少。曹平方等[4]建立了一种改进型的单场站和多车辆路径数学模型,并使用分支界定法求解旅行商问题。以上文献为研究生鲜产品配送提供了理论支撑。
国内外学者多以启发式算法求解生鲜配送问题。范立南等[5]以农产品冷链总成本最小为目标构建VRPTW模型,并使用改进遗传算法求解;Priyantha等[6]以总配送费用最小为目标构建易腐品生产和配送协同优化模型,使用进化算法求解;Amorim等[7]研究了不同配送环境与不同产品变质系数条件下生鲜农产品的新鲜度与配送成本,并使用多目标进化算法求解。从已有文献来看,传统启发式算法在求解时容易出现无法收敛和陷入局部最优等不足,因此本文将建立VRPTW的数学模型,使用CPLEX求解器,采用精确算法中的分支定界算法(Branch-and-Bound algorithms,B&B)求解小规模生鲜配送问题。
1 问题描述与模型构建
VRPTW可以描述为:一个配送中心有一系列匀质车辆,车辆从配送中心出发,依次为顾客提供配送服务,服务完最后一个顾客后返回配送中心。VRPTW须在一定约束条件下(如时间约束和容量约束等),求出最优化函数(如最小化行驶成本和最小化行驶时间)。VRPTW可以用有向图G=(N,A)来描述,其中N={0,1,1,2,…,n,n+1}为节点集,A={(i,j)(i,j)∈N,i≠j}为边集合。N由配送中心“0,n+1”和一组客户N′=N\{0,n+1}组成,δ-(i)和δ+(i)分别代表流入和流出i的点集合,S为客户集的子集。
配送中心有一系列容量为Q的同质车辆K={1,2,…, k}。车辆从配送中心0出发,访问顾客点i,然后到达顾客点j并离开,为最后一个顾客提供服务后返回配送中心n+1。同一路线上所有产品的总需求不能超过每辆车的容量Q。每个顾客的需求qi是确定的,并且必须在一次配送服务中得到满足。
对于顾客点i,车辆的到达时间为ai,等待时间为wi,开始接受服务的时间必须在[ei,li]范围内,其中ei和li分别为顾客点i的最早开始接受服务的时间和最晚开始接受服务的时间。如果车辆在ei之前到达顾客点i,则必须等到ei开始服务。车辆在顾客点i的服务时间为si。在两个节点i,j之间,车辆的行驶时间为tij,行驶距离与行驶成本cij成正比。定义配送中心0和n+1的需求为q0=qn+1=0,时间窗为[e0,l0]=[en+1,ln+1],服务时间为s0=sn+1=0,配送中心0和n+1的距离为c0,n+1=t0,n+1=0。研究目的就是在满足顾客要求的前提下找到一系列行驶路径使总行驶成本最小。VRPTW的模型构建为:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
ei≤ai+wi≤li,?i∈N′ (8)
wi=max{ei-ai,0},?i∈N′ (9)
(10)
∈{0,1},?i,j∈N,k∈K (11)
式(1)为目标函数,使行驶成本最小化。式(2)至式(5)为车辆路径优化问题的传统约束条件,其中式(2)表示每个客户只能被一辆车服务一次,式(3)表示车辆必须从配送中心0出发,式(4)强调路线的连续性,式(5)消除子路径。式(6)的约束条件是指车辆在完成任务后必须返回配送中心n+1。式(7)至式(9)的约束条件表示车辆开始服务的时间限制。式(10)的约束条件保证了同一路线上所有产品的总需求量不超过车辆的容量,式(11)的约束条件定义决策变量。
2 实验结果与分析
为测试CPLEX求解VRPTW的求解性能,需利用相应算例进行实验分析。在此共采用四组算例:2.1中,采用25个点顾客点的Solomon标准测试算例;2.2采用文献[3]算例;2.3采用文献[5]算例。实验采用CPLEX Studio IDE编程,在Windows10 X64操作系统、i5 7200U CPU、2.50 GHz、12 GB内存环境下运行。
2.1 与已知最优解对比
由于Solomon基准测试数据在研究VRPTW时具有权威性,为验证本文数学模型的可行性与有效性,将采用CPLEX求解Solomon 25个点中C1类,并与已知最优解进行对比,求解结果如表1所示。
结果表明,CPLEX求解结果和Solomon算例已知最优解完全一致,这既验证了本文VRPTW模型的可行性和有效性,也验证了分支定界算法的高效性和优越性。
2.2 算例1结果对比
CPLEX与文献[8]和[9]中所提算法的求解结果如表2所示。设置CPLEX求解时间为56.46 s(其他7种算法平均求解时间),运行10次,得到最优路径长度为1 004.32 km,车辆数为6辆。CPLEX的最优结果比其他7种算法的结果分别优化了16.44%,13.23%,15.56%,22.18%,11.64%,9.19%,7.88%,可见CPLEX求解结果的优越性。
文献[8]中单点单亲遗传混合蚁群算法求解最优路径图如图1所示。CPLEX在56.46 s内求解的最优路径为0→ 7→5→14→0;0→1→16→8→0;0→4→15→9→
0、0→18→11→3→0;0→12→19→6→13→0;0→10→20→17→2→0,其中0代表配送中心,1~20代表顾客点,路径图如图2所示。
2.3 算例2结果对比
CPLEX与文献[3]中所提算法的求解结果如表3所示。在对比结果中,CPLEX求出的最优解为522.34,均低于其他3种算法的最小费用。CPLEX得到的最优结果比文献[10]中的结果优化了10.80%,比文献[11]中的结果优化了7.90%,比文献[3]中的结果优化了7.10%。
CPLEX求解的收敛图如图3所示,其在26秒完全收敛,得到全局最优解,这说明CPLEX求解能力较强。
3 结 论
本文以生鲜产品配送为背景,针对VRPTW建立了以行驶成本最小为优化目标的数学模型,并使用CPLEX中的分支定界算法求解。在与Solomon标准算例和其他文献结果对比时,CPLEX求解小规模算例时结果较优,求解时间较短,求解优势明显;但在求解大规模算例时效率较低。因此,使用CPLEX中的分支定界算法求解小规模生鲜产品配送问题具有可行性。未来研究中将继续考虑温度、新鲜度等因素的影响,使问题更贴近现实生活,并研究更高效的算法求解大规模生鲜产品配送问题。
参考文献:
[1] 刘长石,周鲜成,盛虎宜,等.生鲜电商配送的TDVRPTW研究:基于经济成本与环境成本兼顾的视角 [J].控制与决策,2020,35(5):1273-1280.
[2] 方文婷,艾时钟,王晴,等.基于混合蚁群算法的冷链物流配送路径优化研究 [J].中国管理科学,2019,27(11):107-115.
[3] 叶勇,张惠珍.求解带时间窗车辆路径问题的狼群算法 [J].公路交通科技,2017,34(10):100-107.
[4] 曹平方,李灵,李诗珍.基于分枝界定的VRP模型精确算法研究及应用 [J].包装工程,2014,35(17):97-101.
[5] 范立南,董冬艳,李佳洋,等.基于生鲜农产品的冷链物流配送路径优化 [J].沈阳大学学报(自然科学版),2017,29(2):125-131.
[6] DEVAPRIYA P,FERRELL W,GEISMAR N. Integrated production and distribution scheduling with a perishable product [J].European Journal of Operational Research,2016,259(3):906-916.
[7] AMORIM P,ALMADA-LOBO B. The impact of food perishability issues in the vehicle routing problem [J].Computers & Industrial Engineering,2014,67:223-233.
[8] 刘云,张惠珍.多目标带时间窗的车辆路径问题的单亲遗传混合蚁群算法 [J].公路交通科技,2016,33(6):95-100+106.
[9] 殷亚,张惠珍.求解带硬时间窗的多目标车辆路径问题的多种混合蝙蝠算法 [J].计算机应用研究,2017,34(12):3632-3636.
[10] 钟石泉,贺国光.有时间窗约束车辆调度优化的一种禁忌算法 [J].系统工程理论方法应用,2005(6):522-526.
[11] 李琳,刘士新,唐加福.改进的蚁群算法求解带时间窗的车辆路径问题 [J].控制与决策,2010,25(9):1379-1383.
作者简介:李俊(1998—),男,汉族,江西九江人,硕士研究生在读,研究方向:智能算法。