吴玉龙,卓嘎,扎西平措,赵智龙,吴绍干
(西藏大学,西藏 拉萨 850000)
0 引 言随着全国信息化的发展,OCR技术已经越来越普及,但在我国少数民族地区所使用的语言依然信息化不成熟,而藏文作为藏族人民日常交流的主要语言,藏文OCR技术却依然不成熟,因此,研究藏文字符识别是很有必要的,本文使用希尔伯特曲线与最邻近算法识别藏文数字字符,以求利用更少的资源来实现更高的识别率,为藏文的信息化出一份力。
1 基本原理1.1 希尔伯特曲线希尔伯特曲线是一种空间填充曲线,它是由德国数学家David Hilbert(1862—1943)发现,之后的扩展应用有希尔伯特变换和希尔伯特黄变换,希尔伯特变换经常被应用于基础信号的处理上,连续时间信号的希尔伯特转换()输出响应()该信号在通过具有脉冲响应的线性系统之后的()=1/.
希尔伯特曲线被构造成当迭代次数为1时,将正方形分成四个相等的小正方形,然后从左下角的小正方形开始,到右下角的小正方形结束,依次将小正方形的中心与线段连接起来。当迭代次数为2时,每一个小平方被分成四个相等的小平方,然后使用上述方法,操作中心被无限连接以填充整个曲线。结果表明,一维形式下的相邻特征点在二维形式下仍处于相邻位置,最大限度地减少了对原有数据结构的破坏。再结合最邻近算法就能实现KNN算法的最好效果,图1是一阶希尔伯特曲线到八阶希尔伯特曲线的展示图。
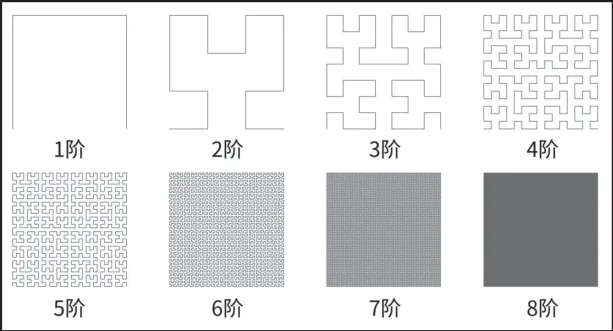
图1 一阶希尔伯特曲线到八阶希尔伯特曲线
1.2 最邻近算法(KNN)[3]KNN(K-Nearest Neighbor)是K最近邻居的分类法,它结合K最接近的历史记录来识别新纪录。KNN是一种经典的分类统计方法,在早期的研究策略中被用于文本分类。在本文中,我们提出了一种基于改进的聚类算法的文本分类方法。KNN算法的基本思想是,在添加新数据之后,训练最接近新数据集的数据根据种数据所属的类别确定与新添加数据相同的类别。
该KNN算法的核心思想是,如果特征空间中最邻近的大多数样本都属于一个类别,则该样本也属于该类别并具有该类别中样本的特征。此方法的分类决策仅基于最近的样本或样本的类别。在一些情况下,如果一个样本在类别决策时的类别与它周围有限的样本中的每一个类的样本的平均值和标准差都可以在决策时直接计算得到。在类别决策时,KNN方法只适用于极少数相邻的样本。因为KNN方法依赖于有限数量的相邻样本而不是判别类域,所以KNN方法比其他方法更适合于类间重叠或更多重叠的待分样本集。该算法的主要缺点之一是,当样本容量不平衡时,例如当一个类有较大的样本容量而其他类有较小的样本容量时,当输入一个新的样本容量时,样本邻域中的样本容量可能占大多数。这种方法的另一个缺点是计算量大,因为对每一个要待分类的文本来说,计算到所有已知样本的距离是为了得到其最近的近邻。目前,对KNN算法的改进可分为四类:一类是用距离函数找到更接近实际的距离来代替标准的欧氏距离,如加权欧氏距离。其次,选择比较合理的值时,通常采用奇数来尝试,一般方法是试错比较,也可采用自适应选择的选择方法;第三,采用更精确的概率估测方法,用多数代替少数的选择机制。本文对现有的一些改进方法进行了总结和分析,并指出了目前研究的热点和难点,提出了未来的研究方向。四是建立一个能提高KNN算法运行效率的有效索引,可以通过KD树等方法进行加速。在对已有的几种典型的基于样本相似度的类别决策方法进行比较和评估方面,已经有很多改进方法被提出来。还有一些改进方法将上述许多方面结合起来。
2 数据采集及文本预处理在数据采集的过程中,我们使用统一7行7列的方格纸采集藏文数字,再利用Python程序语言对采取的数据进行统一的灰度化处理与转文本处理,转换后的文本为行列都为32的文本文件在转化为文本时,我们使用希尔伯特曲线将32行32列的文本数据转化为1行1 024列的数据,在此处采用希尔伯特曲线的原因是相较于传统以行列为标准的变换方式,希尔伯特曲线在变换后能显然提升KNN算法的处理速度以及处理数据的精确度。图2是灰度化处理后的数据,在灰度化时,我们采取图像处理软件将图片对比度调整为黑白。图3是转换完成之后的文本图片,我们将图片数据中白色像素点转换为文本1黑色像素点转化为文本0,最后得出32行32列的文本数据。本实验主要采集了藏文基础字符三十个数据共1 292个其中训练数据集分配数据1 200个测试数据集分配数据92个,其中三十个字符不平均分布。

图2 灰度处理后

图3 转文本后
3 模型构建在如图4所示的实验模型中描述了本次实验的主要步骤,而其中的核心内容为降维方法和KNN算法,传统KNN算法的步骤一般为以下四步:(1)根据已知的训练集重新分类。(2)在训练集中挑选出与测试集最相似的个类型。(3)在测试集的个邻居中依次计算每个类的权重。(4)比较类的权重将文本分到权重最大的那个类别中。
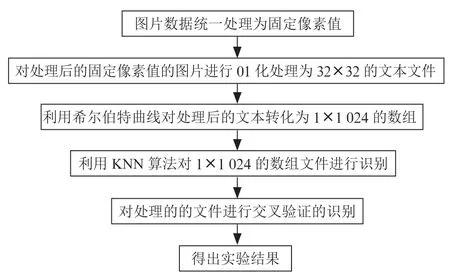
图4 实验模型
在数据分类中使用字符类型_第几个字符的命名方式,在训练中分别测试值为1、3、5、7、9为值测试测试数据集的识别率,再采用交叉验证的方法来反复实验。
4 评估方法目前一般的分类器的评估指标有分类正确率:定义为分类的数据正确的和所有分类数据的比例,影响分类正确率的因素有数据集的数目,属性中的信息,测试数据集的分布情况等。其他的评估指标还有平均准确率、查准率、查全率,在本文中的分类模型中,由于采用了KNN算法,所以模型不具备训练功能,所以影响实验结果的主要因素还是数据集的分布和数据集的质量。
5 实验结果5.1 数据样本在字符识别的过程中所采用的图片样本均来自于手动收集的图片样本,共计1 920个高清图片,源数据的图片像素值为160×160,压缩处理后的图片数据的像素值为32×32,共计1 024个像素点。图片数据分为两个部分,第一个部分有1 200个数据,第二个部分有92个数据,两个部分内的字符数据不平均分布,分别存放在两个文件夹中。
5.2 数据预处理在灰度图片转化为文本的过程中使用三个RGB值与127相除后相加后是否为0判断灰度值为0还是1,当所计算后的值为0则将所计算的像素值转化为数值1,否则转化为0。
5.3 实验环境本次实验的环境在软件为Visual Studio Code,程序环境在Python3.8中,在实验中使用了Python PIL库和Numpy库以及更多的一些处理数据的函数。
5.4 实验过程首先对实验数据进行预处理,预处理完成之后,首先使用传统KNN算法对处理后的数据进行识别,在训练阶段,将1 200个数据按照字符顺序命名排列,之后放入模型中进行识别,得出实验结果如图4,然后使用H-KNN对所处理后的数据做重新识别,然后对所得结果与传统KNN所识别的结果进行对比,在识别时对值分别取1、3、5、7、9对实验结果进行对比,对比表如表1所示;从表1中可以看出相较于传统KNN算法,H-KNN对相同情况下的数据识别率更高,这种结果直接证明了相较于传统KNN算法,H-KNN对藏文字符有更好的识别率。
实验结果见表1。从实验结果看在值为3、5、7时识别正确率比较高,且在值为3、5、7时识别正确率相同,分析此次试验结果,相较于传统CNN、BP神经网络、SVM支持向量机的识别率远远不如,究其原因,有几个方面,一方面是数据量少,另一方面没有在KNN算法上做重大改变,导致其与传统的KNN算法并无太大差别;所以我们总结了以下结果,预处理的数据完成度对实验的结果非常大,这其中的影响因素有所处理的数据是否统一,字体是否相同,所处理后的数据的像素大小,图片压缩后的信息保留程度,和灰度图片的处理之后的颜色校正,字体是否倾斜,由于图片处理后的像素格特别少而其中的有效信息就更加少,所以每一个小的因素都会影响识别率,所以我们在这里不与其他算法的识别率做比较,而是与传统的KNN算法和本次实验所采用的H-KNN算法进行比较,其结果显示相较于传统KNN算法H-KNN算法在识别率上有明显的提升,以此验证了此种算法的可行性及有效性。
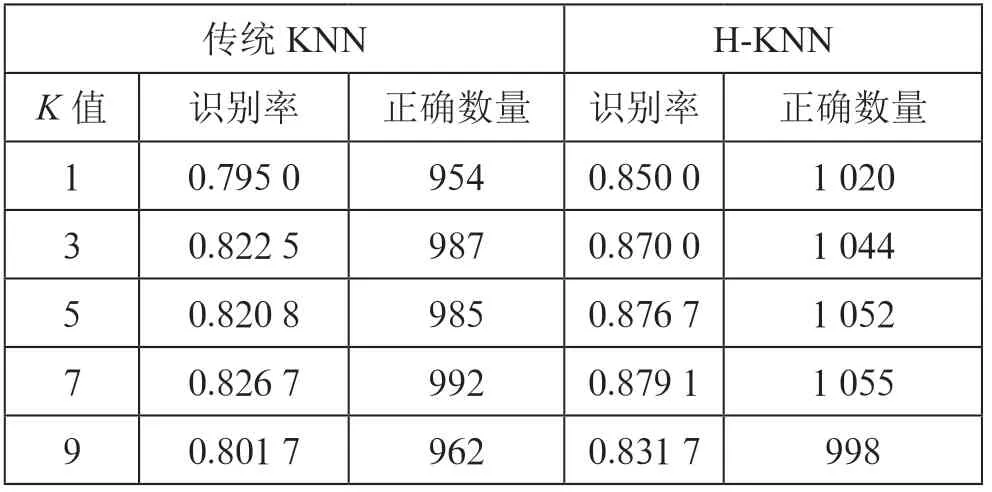
表1 传统KNN与H-KNN对比
6 结 论藏文字符的识别对于藏文的信息化有着关键的作用,在信息化愈发成熟的今天,研究藏文字符识别有着很大的意义,本文识别的一次实验性质的实验,虽然未有很好地识别效果,但为藏文字符识别提出了一种新的方法,希望为藏文字符的研究添砖加瓦,贡献属于自己的一份力量。

