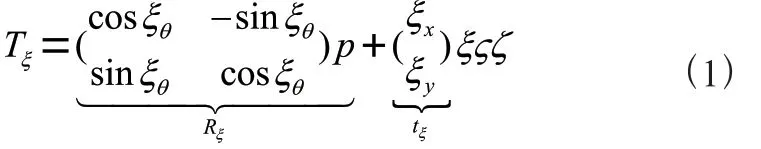


收稿日期:2023-06-28
基金项目:安阳市科技发展计划(2022C01SF117);安阳工学院科研基金(YPY2022011)
DOI:10.19850/j.cnki.2096-4706.2024.05.040
摘" 要:为实现仓储环节的自动化操作,对多AGV路径规划进行了研究,使用栅格地图法构建地图环境,以单路径A*搜索算法为基础,采用双层路径规划的冲突搜索算法解决多AGV路径冲突问题。具体实施方法是在高层进行冲突检测和添加约束,在底层使用A*算法进行单路径规划。最后使用Python的matplotlib库编程对路径规划算法进行仿真。仿真结果表明,该课题所使用的规划方法行之有效。
关键词:路径规划;CBS算法;A*算法;AGV;栅格地图
中图分类号:TP18" " 文献标识码:A" 文章编号:2096-4706(2024)05-0183-07
Multi-AGV Path Planning Based on Conflict Search
WEI Shengli, ZHANG Tao
(School of Computer Science and Information Engineering, Anyang Institute of Technology, Anyang" 455000, China)
Abstract: In order to achieve automated operations in the warehousing process, research is conducted on multi-AGV path planning. A grid map method is used to construct a map environment, and based on the single path A* search algorithm, a conflict search algorithm for dual layer path planning is adopted to solve the multi-AGV path conflict problem. The specific implementation method is to perform conflict detection and constraint addition at the upper level, and A* algorithm is used at the lower level for single path planning. Finally, it uses Pythons matplotlib library programing to simulate the path planning algorithm. The simulation results indicate that the planning method used in this project is effective.
Keywords: path planning; CBS algorithm; A* algorithm; AGV; grid map
0" 引" 言
迅速增长的快递业务对物流业提出了更高的要求,传统的手工操作,难以满足快速变化的市场需求[1]。为了解决仓储环节的自动化问题,通常采用自动导引车(AGV)来实现高效快捷的快递配送[2],以达到自动化、智能化和高度无人化操作[3]。而多AGV路径规划问题也就成为研究的重点。目前路径规划算法普遍基于A*算法,多路径规划基于冲突搜索的思想。李扬在A*算法的基础上提出了基于冲突搜索的多智能体路径规划算法[4]。宣志玮等针对地形复杂的大型地图,提出了CBS框架下面向复杂地图的低拓展度A*算法[5]。官祥锦等采用切比雪夫距离对A*的启发函数进行加权,减少了搜索时间,并结合时间窗模型,有效解决了多AGV冲突问题[6]。周欣慈等提出了一种改进的CBS算法对码头的AGV路径规划进行了研究。其核心思想是结合二叉树原理建立冲突树来规避多AGV的冲突[7]。
在前人研究的基础上,对多AGV路径规划问题进行了研究。首先对单AGV路径规划问题进行了分析,然后将其扩展应用到多AGV路径规划问题。使用了双层路径规划算法以解决冲突问题,每个AGV都在底层搜索中找到最佳行驶路线,而把解决AGV路径之间的冲突放在高层搜索中。
1" 地图选择与单AGV路径规划
AGV路径规划需要研究两个重要问题:环境地图建模方法和AGV路径规划算法。环境地图能够定量判断所选择的路径规划算法成本,路径规划算法求出最优的行走路径。单AGV路径规划是多AGV路径规划的前提。本节内容介绍环境地图建模方法和单AGV路径规划算法。
1.1" 环境地图建模
环境地图模型的准确性和复杂程度会影响路径规划的决策效率和响应速度[8]。常见的环境地图建模方法包括可视地图、拓扑地图和栅格地图。栅格图法是近年来被广泛采用的AGV环境模拟方法。如图1所示,它将空间环境分成相同大小的格子,一些有障碍物的格子和其他开放的格子。栅格大小的选择很重要,过小会增加内存使用量,而过大会减少精度和影响路径规划。在栅格地图上,起点到终点之间连续的可通行栅格构成AGV的一条可行路径。栅格图法是一种简单高效、易实现且易于观察的建模方法,适用于复杂环境下的路径规划。因此,本文采用栅格法建立二维平面地图模型,并通过算法实现AGV路径规划模拟。
图1" 栅格图模型
1.2" 单AGV路径规划算法
单AGV路径规划是多AGV路径规划的基础。单AGV路径规划只考虑一台AGV运行时的最优路径,以达到有效、高效地执行任务的目的。A*算法、Dijkstra算法和粒子群算法是研究应用较多的路径规划算法[9]。
Dijkstra算法最开始主要用于求解有向图的最短路径问题,后来又被用作单源路径规划算法,对单AGV的路径规划研究具有重要意义。然而,它在实时路径规划时需要大量的计算量,这是它的主要缺陷。1968年,Nilsson等提出了A*算法。它是一种求解最短路径的直接算法,也是其他许多启发式算法的基础。粒子群算法是一种基于群体智能的优化算法,用于在搜索空间中寻找最优解。粒子群算法简单易实现,并行化效果较好并且全局收敛性较强。但在搜索过程中,粒子只能基于当前状态和历史最优状态进行更新,而无法引入其他信息来帮助搜索,容易陷入局部最优解,并且种群的随机初始化对迭代结果也有较大影响。
尽管Dijkstra算法在单个AGV路径规划问题中能够找到最佳路径,但是其运行时间相对较长。粒子群算法容易陷入局部最优解的困扰,并且其结果受到随机性的影响程度相当大。相对于其他算法而言,A*算法具有更高的搜索效率,更好的空间利用率和更广的适用性,A*算法引入启发式函数来指导搜索,估计其他位置到目标位置的距离,并优先探索离目标节点近的节点,因此能够更快地找到最短路径。而且A*算法的启发式函数可以根据具体问题进行设计,因此在不同种类的图中都可以使用。而Dijkstra算法和粒子群算法则只适用于特定类型的图或问题。因此,我们选择A*算法来解决该问题。
1.3" A*算法
1.3.1" A*算法模型
A*算法是一种启发式搜索算法,常用于解决图或网络中的最短路径问题。A*算法引入启发函数用来指导搜索,该函数可以估计从当前位置到目标位置的距离[10],其主要原理选择成本最低的节点作为下一步移动位置,并重复此步骤,直到找到目标点或者确定无法到达目标点为止。启发函数表达式如式(1):
f (n) = g (n) + h (n)" " " " " " " " " " " (1)
其中,n表示当前位置,g (n)表示从起始位置到当前位置n的实际距离,h (n)表示从当前位置n到目标位置的估计距离。f (n)表示总距离。在满足可接受性条件下,A*算法能够得到最优解。
在式(1)中,由于距离函数g (n)已知,因此启发式函数的选择可以基于距离函数和问题特征进行设计,以尽可能减少搜索空间和加速搜索过程。不同的启发式函数可能导致最终评价目标函数的结果不同。当估计函数值h (n)如果设计的太高,虽然可以提高算法的搜索速度,但难以保证算法搜索的精度;而估计函数值h (n)如果设计的太低,虽然保证了算法的精度却难以保证算法的运算效率。A*算法常用的h (n)估计值函数有曼哈顿距离计算函数、欧式距离计算函数。
欧式距离的计算公式如式(2):
(2)
曼哈顿距离的计算公式如式(3):
(3)
在式(2)(3)中,(xn, yn)表示当前位置,(xg, yg)表示目标位置。
在栅格图中,搜索最短路径常用4邻域搜索和8邻域搜索。4邻域搜索只考虑上下左右4个相邻的栅格,而8邻域搜索则考虑上下左右以及对角线方向上的8个相邻的栅格[11]。AGV在仓储中心一般只有横平竖直的运动,不存在斜向移动。因此这里只考虑4邻域搜索,使用曼哈顿距离作为启发函数。
1.3.2" A*算法具体流程
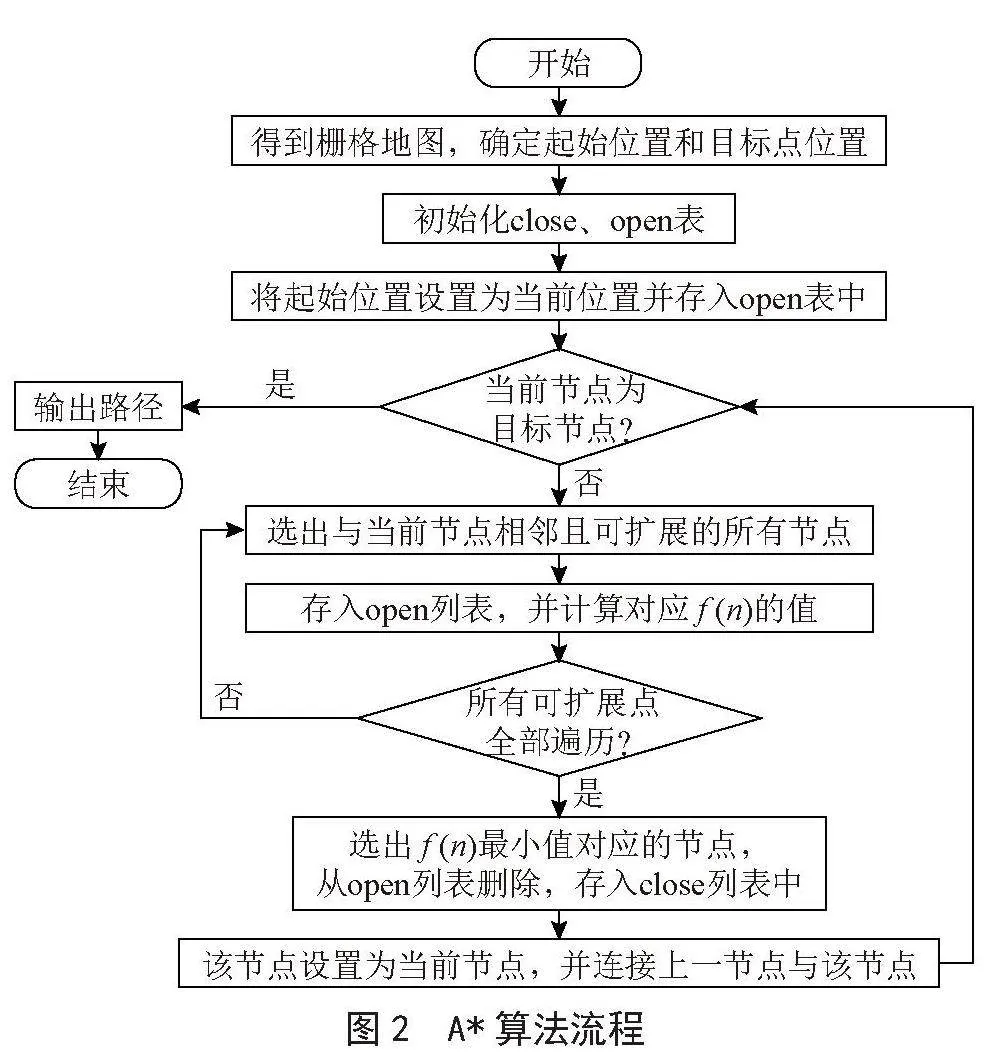
A*算法维护两个列表:一个是OPEN列表,记录待探索的节点;另一个是CLOSE列表,记录已经探索过的节点。首先将起始节点加入OPEN列表,并计算其估计代价。其基本步骤为:
1)初始化起点和终点节点以及起点的估价函数值(即起点到终点的最短距离)。寻找OPEN表中估值函数值最小的节点。
2)将起点加入一个开放列表(open list)中,该列表存储待扩展的节点。
3)从开放列表中选择一个最优节点进行扩展。这里的“最优”是指当前已经走过的路径长度加上该节点到终点的估价函数值最小。
4)将该节点存入关闭列表(close list)中,该列表存储已考查过的节点。
5)对该节点的所有邻居节点进行评估。如果邻节点不可到达或已在关闭列表中,则不处理,否则计算每个邻居节点的估价函数值,并记录它们的父节点为当前节点。
6)对于不在OPEN列表中的邻居节点,将其加入OPEN列表,并将当前节点设置为他的父节点。如果某个邻居节点已经在开放列表中且更新,则更新其父节点为当前节点和路径长度信息。
7)重复步骤3)-6),直到找到终点或者开放列表为空(表示无解)。
8)如果找到了终点,则按照每个节点的父子关系回溯路径;否则输出无解。A*算法流程如图2所示。
图2" A*算法流程
2" 多AGV路径规划
多AGV的路径规划问题在于协作完成任务并避免碰撞。本文采用基于冲突的搜索(CBS)算法解决多AGV的碰撞问题。
2.1" 多AGV路径规划问题模型
在多AGV路径规划问题中,假设有n个AGVA = {a1,a2,a3,…,an}和一个无向图G = {V,E},V表示地图中的节点,E表示节点之间的边。在地图中指定一个起始点S = {s1,s2,s3,…,sn}和目标点T = {t1,t2,t3,…,tn}。每个AGV的输入是三元组〈G,si,ti〉,其中i = 1,…,n。时间被离散化后,在每个周期内AGV可以完成一个动作m,用映射m:V→V来表示m(v) = v。这个动作m使得AGV在一个周期内完成从位置v到位置v的转换。动作有两种类型:等待和前进。等待是指AGV在本周期内在原位置不动。前进是指AGV从当前位置v前进到位置v,即(v,v) ∈ E。按照搜索算法最终会找到一条路径π = {p1,p2,p3,…,pi},其中p1,p2,p3,…,pi ∈ V。
2.2" 路径冲突
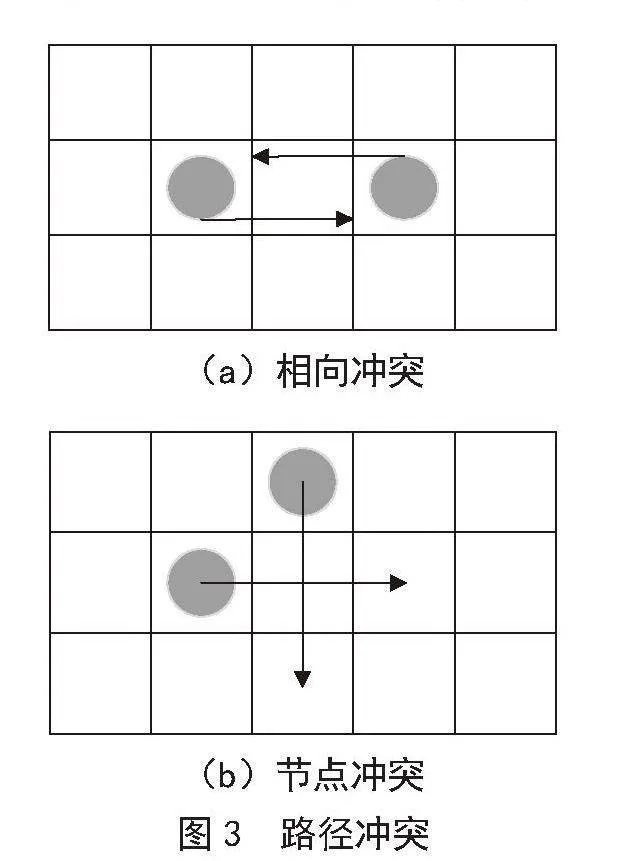
在多AGV环境中,会发生不同类型的冲突。假设仓储系统中所有AGV的匀速行驶,不会发生追赶冲突。本文主要考虑相向冲突和节点冲突两种情况。相向冲突是指两个AGV在相反的方向上移动时发生的碰撞或阻塞情况,如图3(a)所示。节点冲突则是指两个或多个AGV在同一交叉路口或节点处互相阻塞的情况,如图3(b)所示。这些冲突可能导致任务延迟、资源浪费和系统效率降低等问题。
(a)相向冲突
(b)节点冲突
图3" 路径冲突
2.3" 基于冲突的搜索算法
基于冲突的搜索(CBS)算法[12]解决问题的思路是:不断检测是否存在冲突,如果存在冲突,则通过一定的规则解决冲突,直至解决所有的冲突问题。在算法的运行过程中,首先在高层进行冲突检测和约束添加,然后再进入底层进行具体的操作。在底层中使用上一节介绍的A*算法为单个AGV寻找一条与新的限制条件相符的路径。
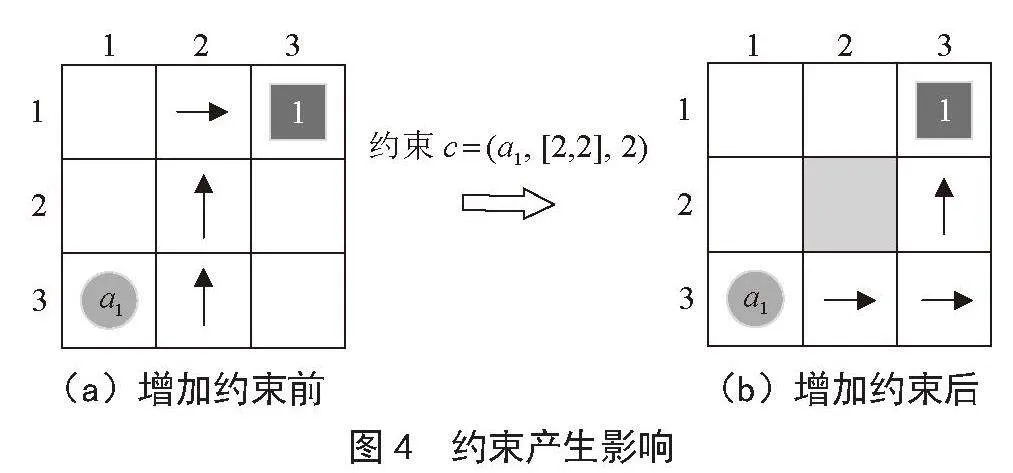
CBS算法引进约束概念,约束用c =(ai,s,t)来表示。其中t表示在某一时间点,对于AGVai而言,s位置被限制,无法经过或停留在上面。向一个3×3的栅格地图中添加一个约束c =(a1,[2,2],2)如图4所示。a1的起始节点为(3,1),目标节点为(1,3),起初路径规划后a1有概率会途径(2,2)节点位置(如图4(a)所示)。然而,添加约束后,在t = 2时刻(2,2)位置不能通过。因此,算法将跳过该障碍物并重新规划路径以符合约束条件(如图4(b)所示)。新路径满足约束条件。
(a)增加约束前" " " " " " " " " " (b)增加约束后
图4" 约束产生影响
在高层搜索中,CBS算法搜索约束树节点(CT Node),而这个节点CT是一棵二叉树。高层设计了一个优先级队列OPENcbs,用于记录待检测的约束树节点,节点的cost代表其解决方案的成本。每个约束树节点N都含有三个数据字段。
N.constraints:一组约束,涵盖了场景中所有AGV的限制条件。CT的根节点包含一个空的限制条件集合,而CT的子节点继承其父节点的限制条件,并为一个AGV添加新的限制条件。
N.solution:路径规划的解,解中所有AGV的路径符合约束树节点的约束集。但可能存在潜在冲突,因此解不一定有效。
N.cost:该节点解的成本,即所有单AGV路径成本的总和。
CBS算法的底层搜索算法是用来为每个AGV规划的,本文采用A*算法,因为下层不考虑冲突,所以所有单AGV路径成本的总和最小。
在CBS算法中,首先需要创建一个根节点R作为约束树的起点,该节点初始时没有任何约束条件,其constraints属性为空,但其solution属性为下一层搜索中各个AGV路径节点的集合,而cost属性则为各AGV路径的成本值之和。在初始解中,每个AGV的路径规划是相互独立的,没有考虑其他AGV路径的影响。之后,算法从OPENcbs队列中获取节点,在获取到的节点N中检查其解是否存在冲突,冲突表现为四元组(ai,aj,s,t),在时刻t时,AGVai和aj在元素s处产生了冲突。如果发现冲突,算法会在该节点N的基础上分解出两个子节点N1和N2,然后将父节点的约束和值从属性上复制到两个子节点上。当对节点N1添加约束c = (ai,s,t),这意味着ai在t时刻不能进入s点,底层重新为ai规划路径,并使用高层搜索更新节点的cost属性。
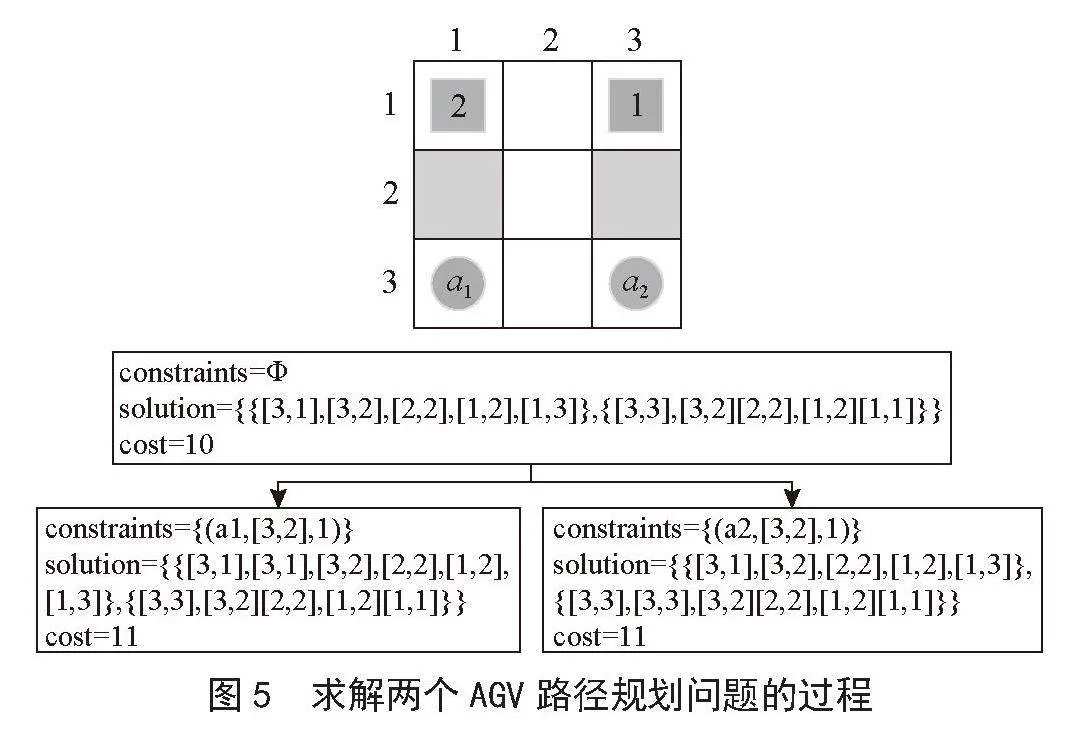
图5给出了两个AGV的路径规划,a1从(3,1)的起始位置出发,前往(1,3)的目标位置,而a2则从(3,3)的起始位置出发,前往目标(1,1)。在初始化阶段,CBS算法上层创建一个空根节点,并把该节点放入到OPENcbs集合中。然后,主循环从OPENcbs中获取根节点,并根据其中的解进行冲突检测。在节点(3,2),a1和a2发生冲突的事实在t = 2时刻发生。因此,算法上层会创建两个子节点,这些子节点将继承父节点的所有限制条件,同时加入新的约束条件。在接下来的操作中,底层为对应的AGV路径重新规划,并将两个子节点加入OPENcbs列表。在下一轮迭代中算法成功找到了无冲突路径。虚线方框内的解表示最佳路径。
图5" 求解两个AGV路径规划问题的过程
3" 路径规划仿真
为检验算法的有效性,使用Python的Matplotlib库编程对路径规划算法进行了仿真。
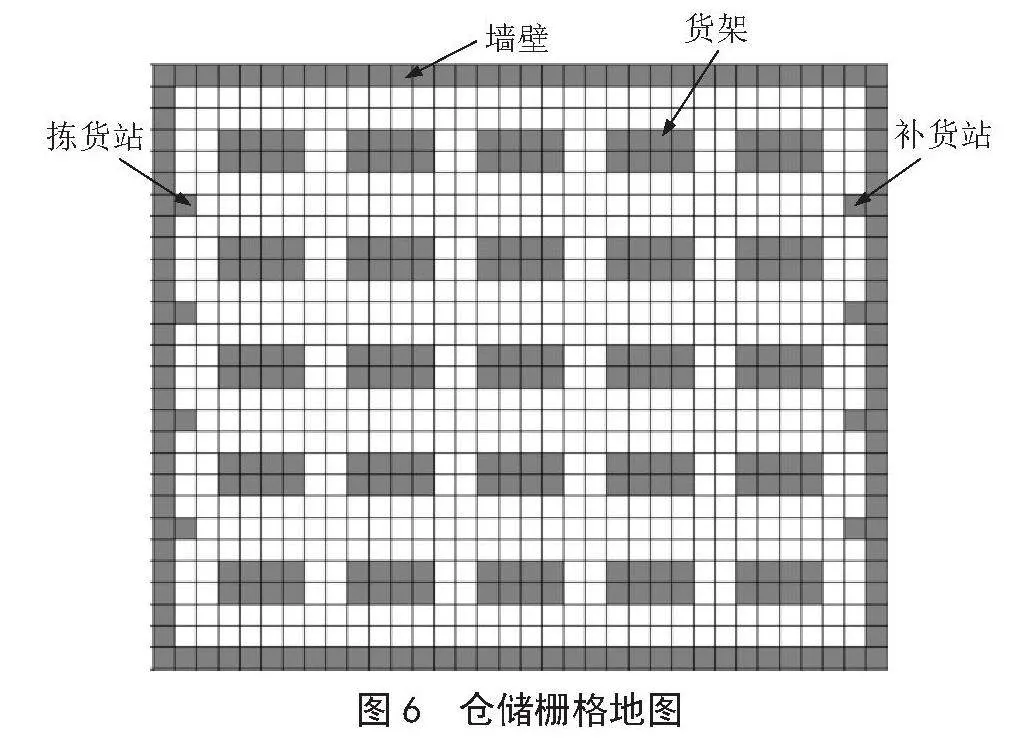
图6展示了一个栅格地图环境,该地图有26行32列、共计832个栅格。周围黑色障碍物代表墙壁。每个栅格形状大小相同,AGV的直径略小于栅格的边长,每个栅格都有位置坐标(x,y),从地图左上角开始,x表示第几行,y表示第几列。AGV经过一个栅格需要花费一个单位时间。拣货站占据4个栅格,补货站占据4个栅格,货架占据200个栅格。
图6" 仓储栅格地图
3.1" 相向冲突仿真实验
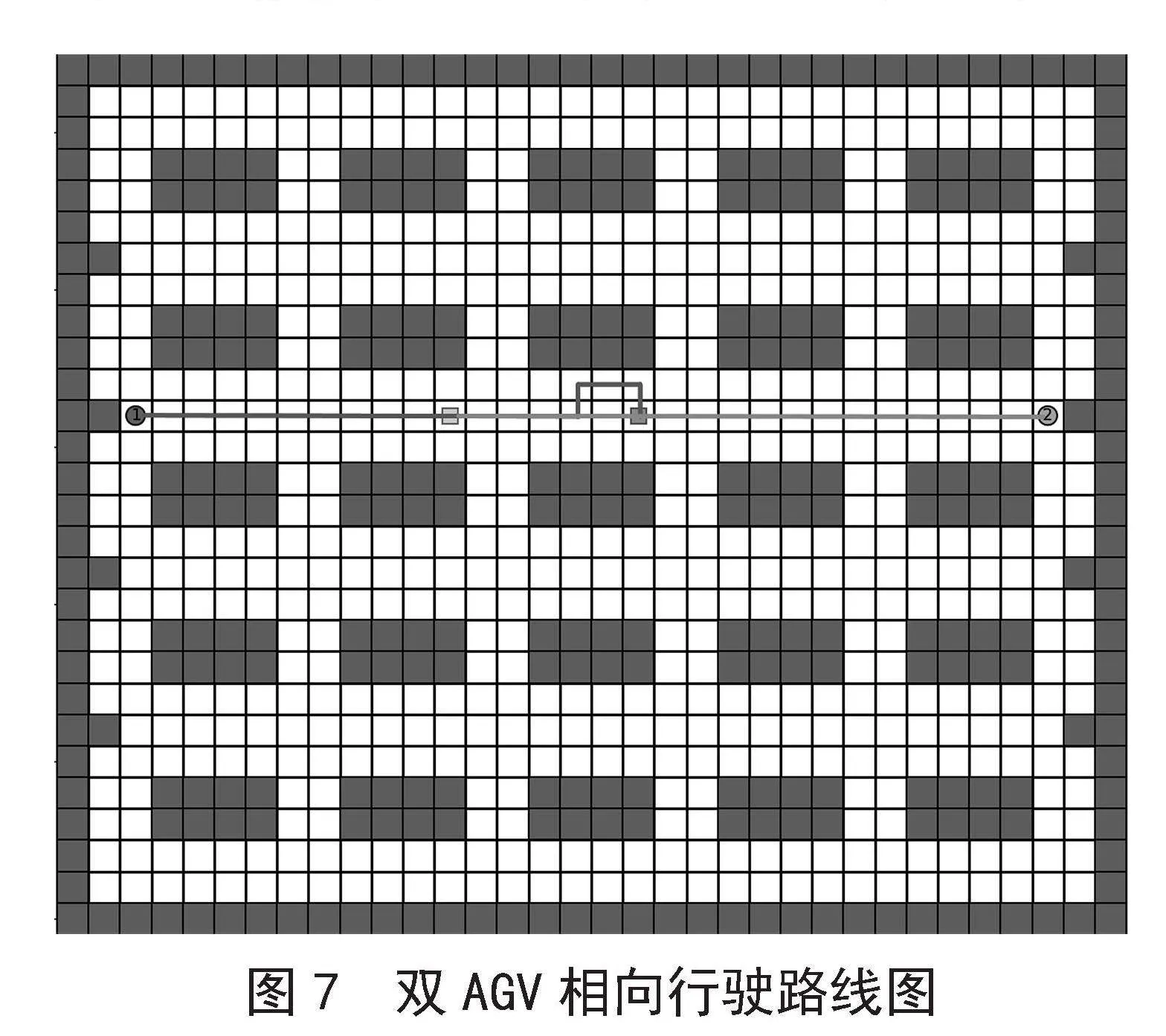
假设两辆AGV同时运行,行驶路线如图7所示。其中,AGV1从起点(12,3)到终点(12,19),AGV2从起点(12,32)到终点(12,13)。为避免与AGV2发生冲突,AGV1选择绕道经过栅格(11,17)(11,18)(11,19),而不是直接到达栅格(12,19)。通过CBS算法,确保二者不会在时间上同时到达任何一个栅格,避免了潜在碰撞冲突。
图7" 双AGV相向行驶路线图
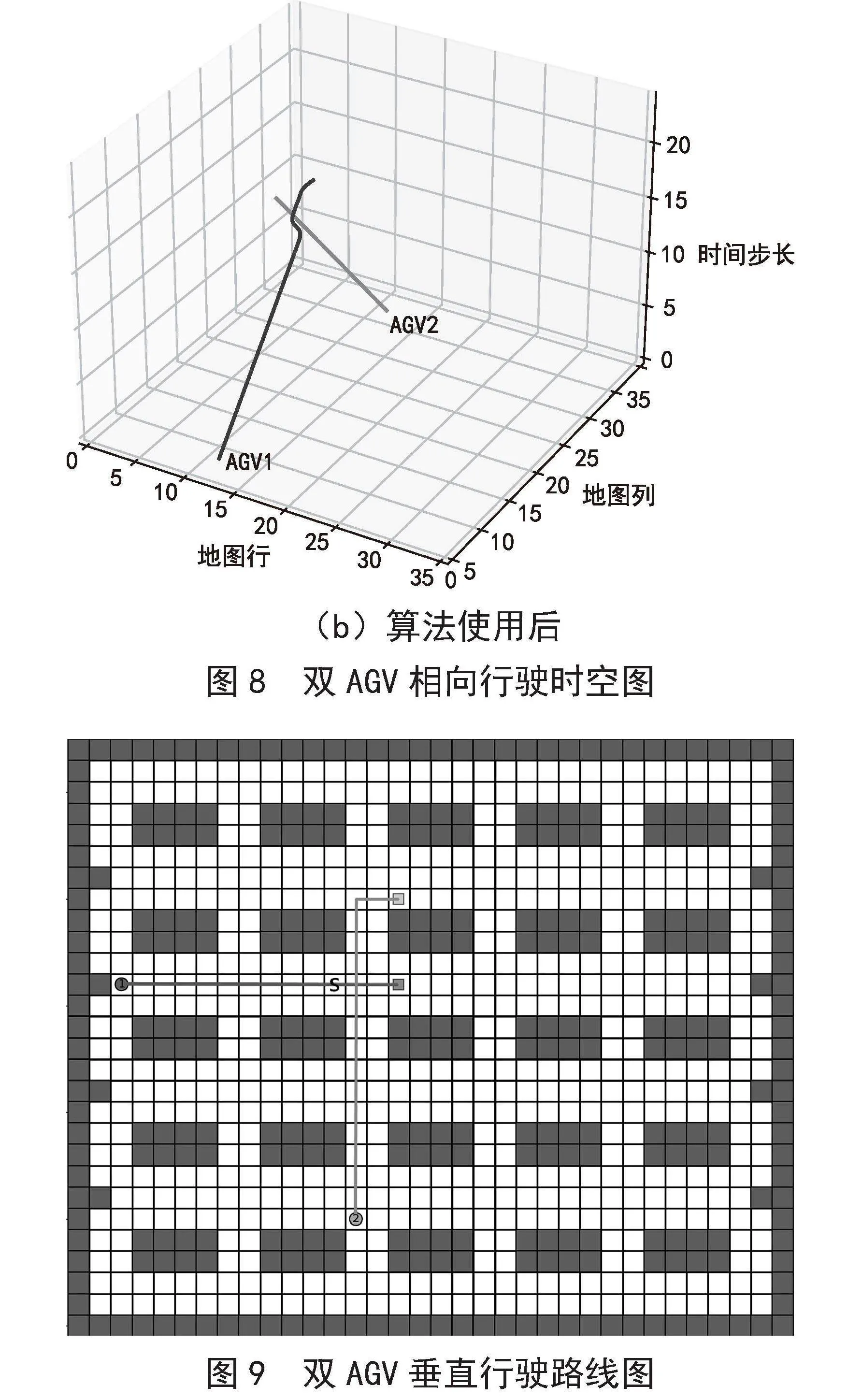
图8展示了这两辆AGV的三维时空图。未使用CBS算法时,如图8(a)所示,两条路径在(12,18,16)相交,说明在t = 16时刻发生了碰撞。使用CBS算法后,AGV1避开了栅格(12,18),行驶到了(11,17),避免了与AGV2相撞,如图8(b)所示。原理为算法上层检测到冲突(a1,a2,(12,18),16),施加新约束(a1,(12,18),16),下层重新规划AGV1的路径。这表明CBS算法可以有效解决相向冲突。
3.2" 节点冲突仿真
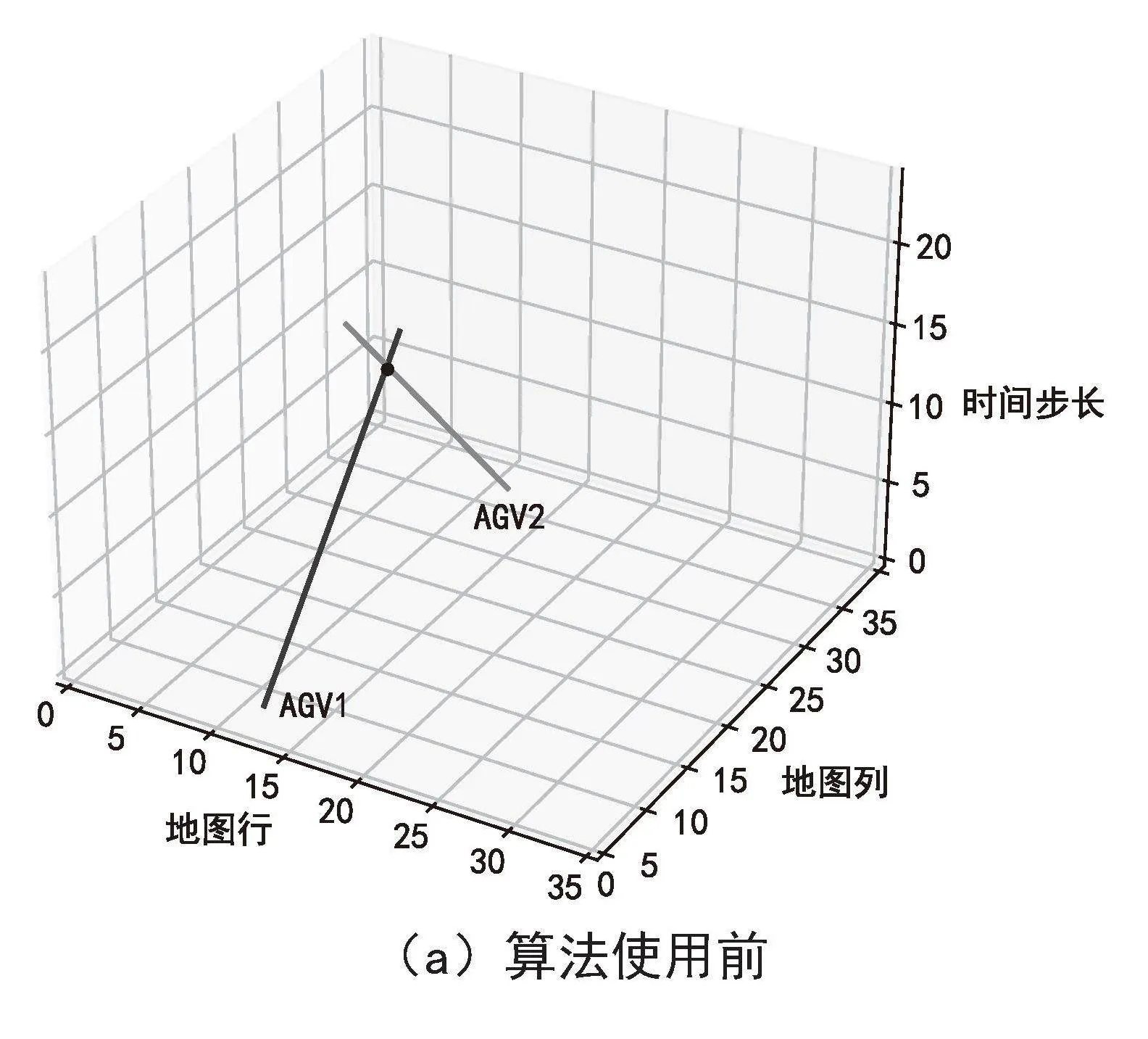
为了验证节点冲突,假设两辆AGV垂直行驶,如图9所示,AGV1从起点位置(12,3)到达终点位置(12,16),AGV2从起点位置(23,14)到达终点位置(8,16)。为避免在栅格(12,14)发生节点冲突,AGV1在行驶到栅格(12,13)(即S点)后停留一个单位时间,让AVG2先行,随后再前往栅格(12,14)。避开了与AGV2在栅格(12,14)发生节点冲突。
(a)算法使用前
(b)算法使用后
图8" 双AGV相向行驶时空图
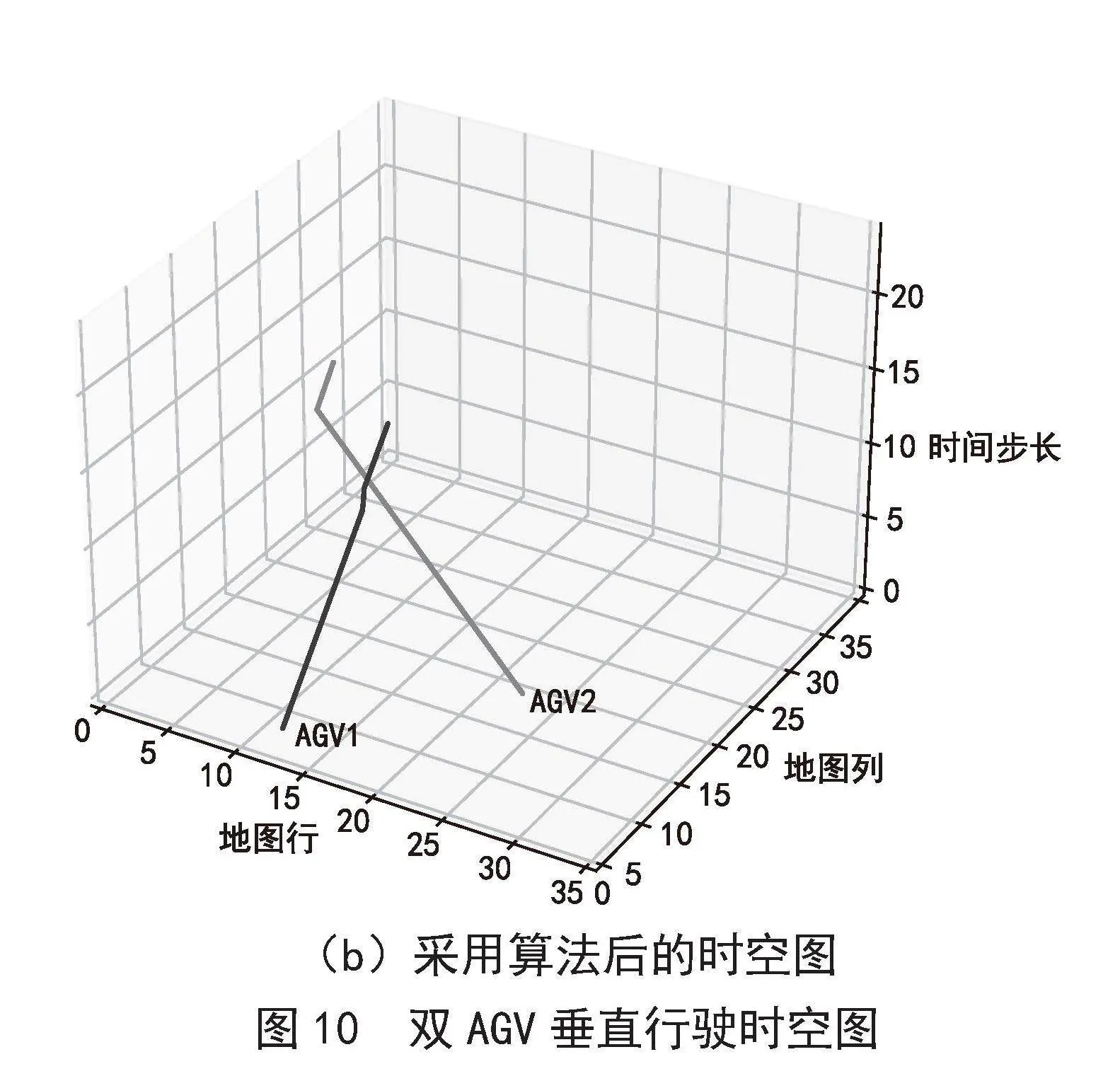
图9" 双AGV垂直行驶路线图
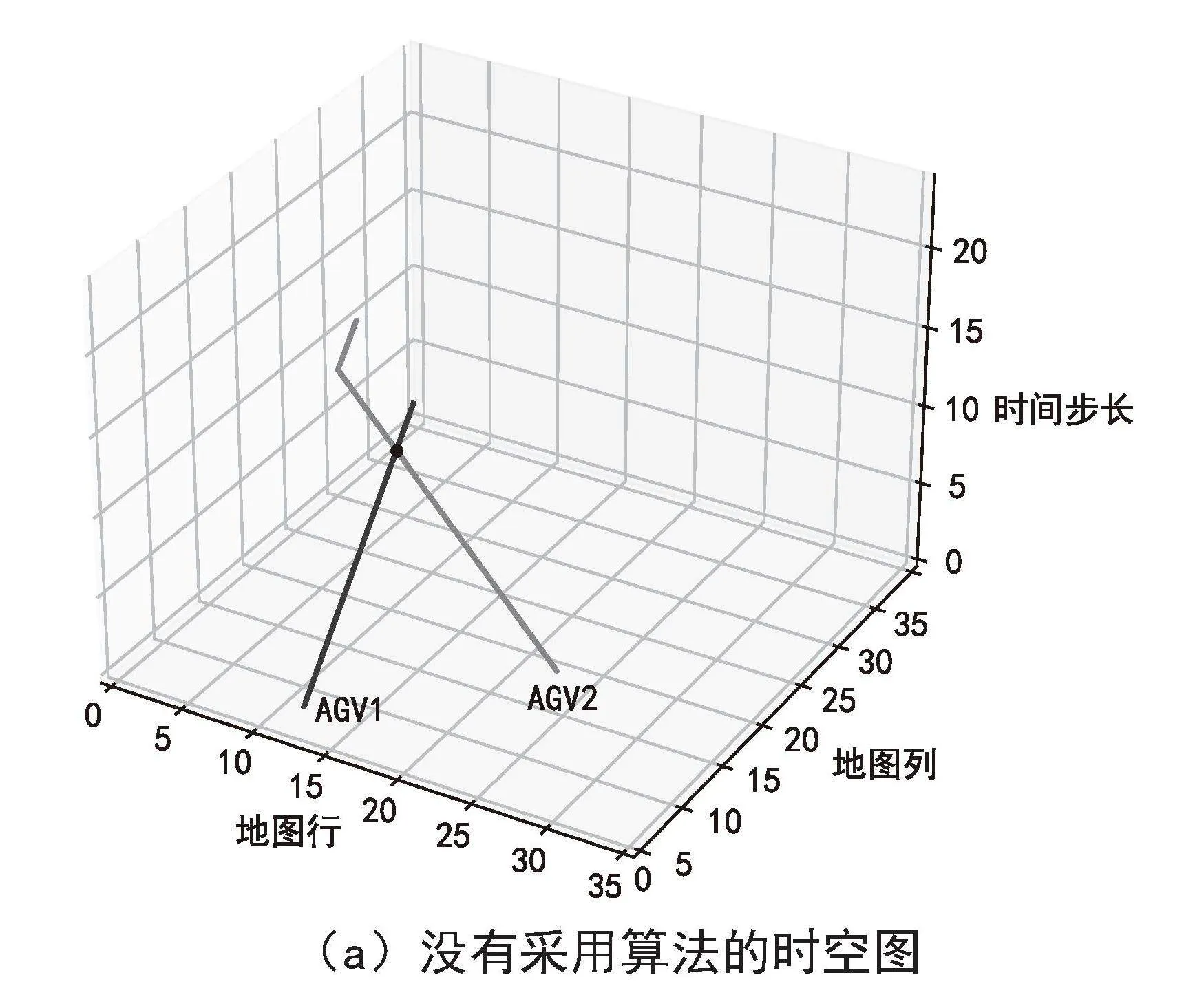
图10展示了节点冲突三维时空图。未使用CBS算法时,t = 11时刻两条路径在(12,14,11)处相交,表明发生了冲突。使用CBS算法规划后,两条路径没有相交,AGV2的路径不变,而AGV1在t = 10时后停止行驶,停留在栅格(12,13)上一个时间单位,让AGV2先行,之后再继续前进,避免了相撞。原理为在上层检测到(a1,a2,(12,14),11),通过添加新约束(a1,(12,14),11),使得在下层重新规划路径以满足约束。结果表明,算法能够有效解决路径冲突。
(a)没有采用算法的时空图
(b)采用算法后的时空图
图10" 双AGV垂直行驶时空图
3.3" 多种冲突的情景
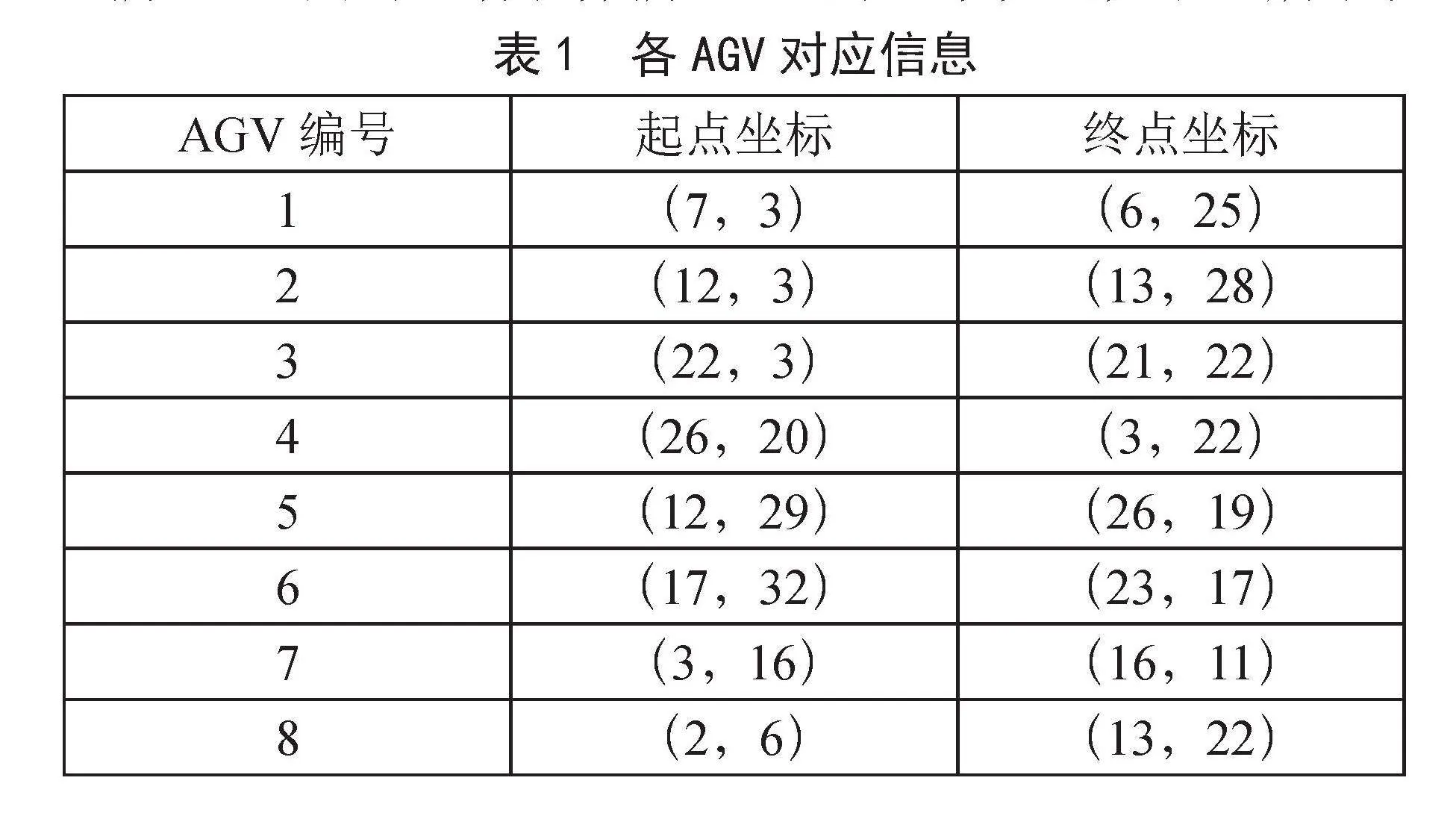
为了检验算法在多种冲突情景下的效果,假设有8辆AGV同时运行,各辆AGV的基本信息如表1所示。
表1" 各AGV对应信息
AGV编号 起点坐标 终点坐标
1 (7,3) (6,25)
2 (12,3) (13,28)
3 (22,3) (21,22)
4 (26,20) (3,22)
5 (12,29) (26,19)
6 (17,32) (23,17)
7 (3,16) (16,11)
8 (2,6) (13,22)
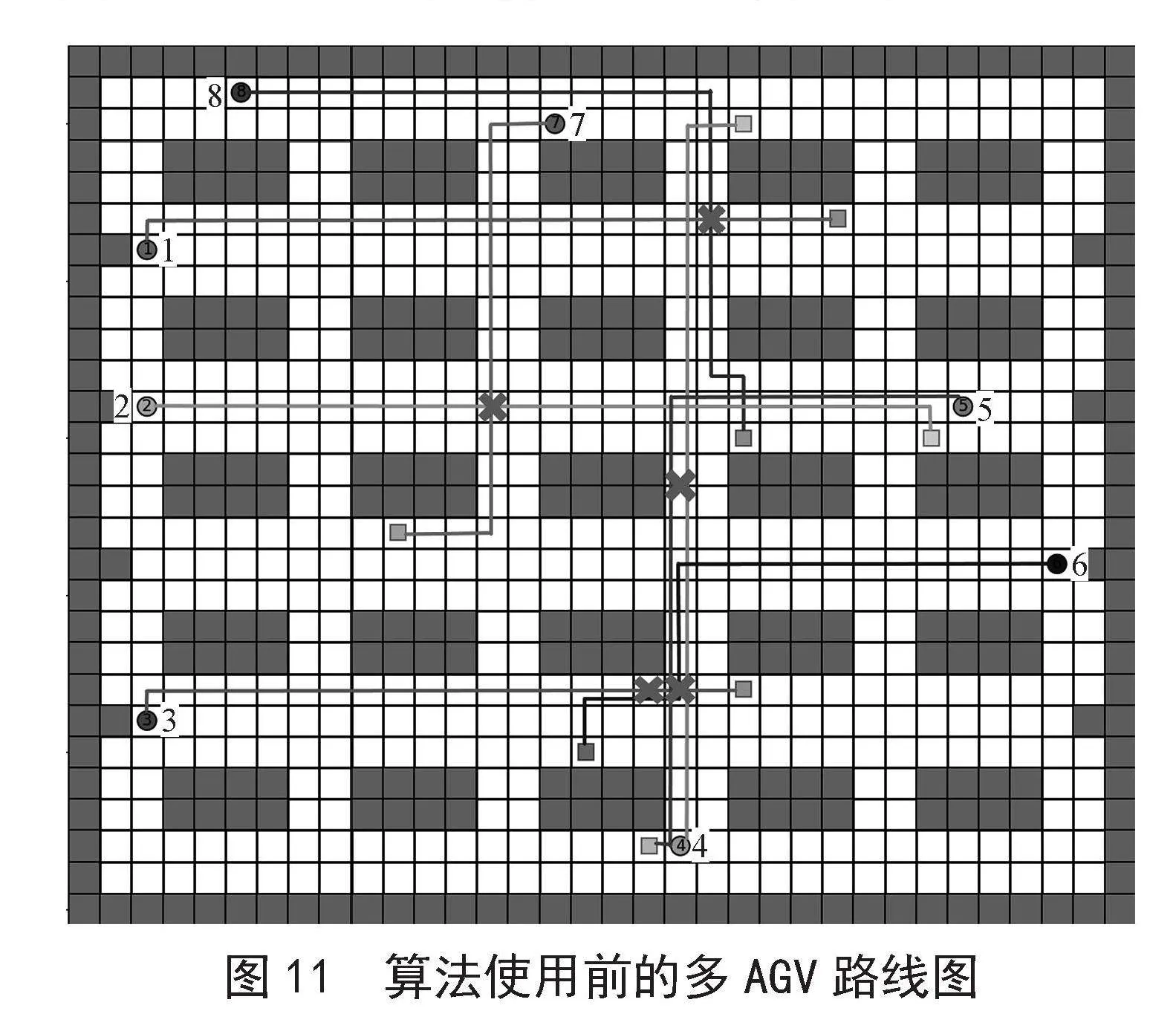
图11展示了未使用CBS算法时所有AGV的行驶轨迹,栅格地图上的圆形代表每辆AGV的起点,方框代表终点,叉号代表该位置发生了冲突。
图11" 算法使用前的多AGV路线图
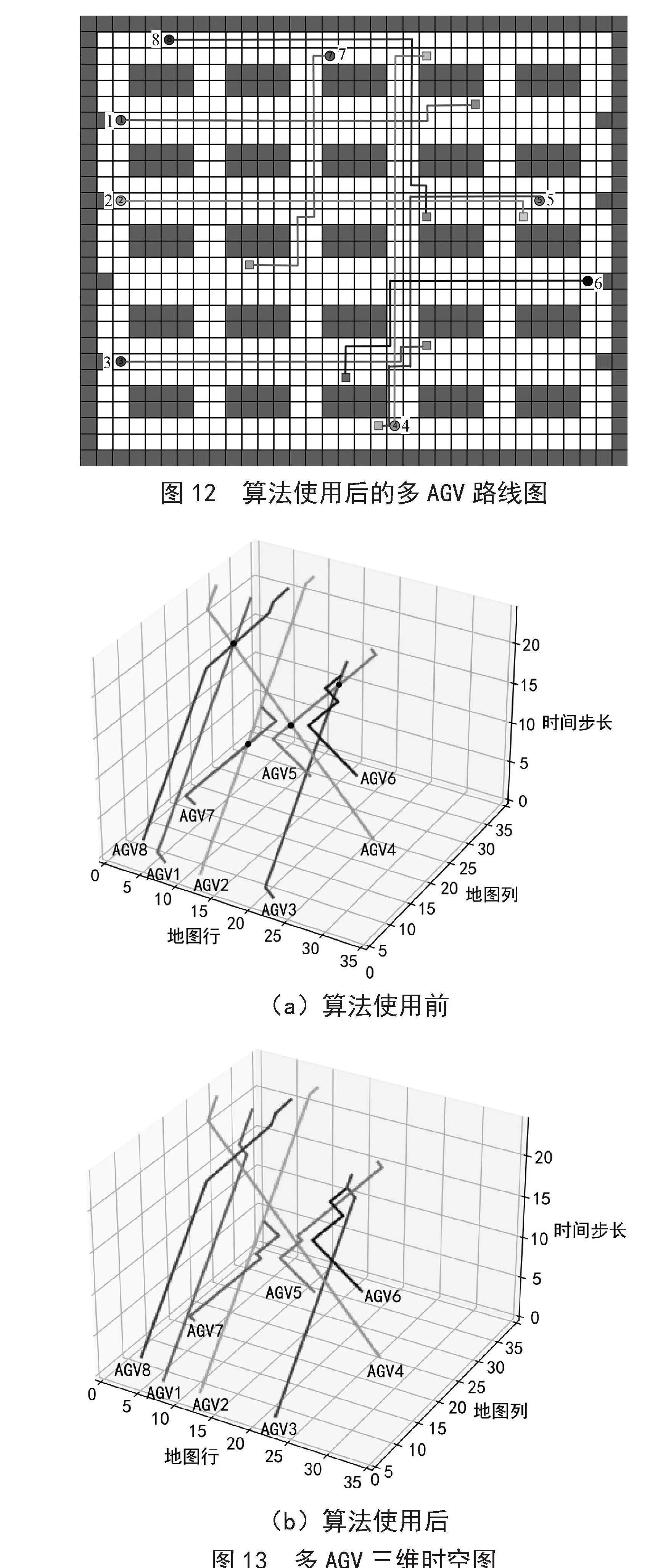
图12展示了使用CBS算法后所有AGV的行驶轨迹,所有AGV没有发生碰撞。
图13展示了中8辆AGV行驶轨迹对应的时空图,共有5个相交点,分别对应图11中5个叉号,代表发生了5次冲突。通过图13(a)可知,在t = 19时,1号和8号在坐标(6,21)处发生碰撞;在t = 11时,2号和7号在坐标(12,14)处发生碰撞;在t = 17时,3号和6号在坐标(21,19)处发生碰撞;在t = 18时,3号和5号在坐标(21,20)处发生碰撞;在t = 11.5时,4号和5号在坐标(14,20)和坐标(15,20)之间发生碰撞。
图12" 算法使用后的多AGV路线图
(a)算法使用前
(b)算法使用后
图13" 多AGV三维时空图
采用CBS算法规划的AGV成功避免了5处冲突。图13(b)展示了CBS算法规划后的路径,任意两条路径线段在时空中均没有相交,说明路径间无冲突。2、4、5和8号的AGV的路径没有变化,而1、3、5和7号AGV为避免冲突重新规划了路径。
通过CBS算法,上层检测到5个冲突,分别为(a1,a8,(6,21),19)、(a2,a7,(12,14),11)、(a3,a6,(21,19),17)、(a3,a5,(21,20),18)和(a4,a5,[(14,20),(15,20)],11.5),施加对应的约束(a1,(6,21),19)、(a5,(21,20),18)、下层根据1、3、5和7号AGV新添加的约束为它们重新规划了路径。证明在存在多种冲突且AGV数量较多的情况下,使用CBS算法仍然能够成功解决问题。
4" 结" 论
针对多AGV作业时遇到的各种冲突问题,采用一种双层路径规划算法进行解决。底层采用A*进行路径规划,高层采用CBS进行冲突监测,实现了算法并对算法进行验证。仿真结果证明了该算法的有效性。主要完成的工作有:
1)选用栅格法作为多AGV路径规划的地图建模方法。
2)采用基于曼哈顿距离预估成本的A*算法实现了单AGV路径规划,为CBS算法奠定了基础。
3)采用CBS算法解决节点冲突、相向冲突和多种冲突并存等问题。
4)使用Python语言实现了算法,对算法的有效性进行了仿真。
参考文献:
[1] 刘冠一.仓储环境下智能移动机器人路径规划研究 [D].北京:北京印刷学院,2021.
[2] KHIR R,ERERA A,TORIELLO A. Two-Stage Sort Planning for Express parcel Delivery [J].IISE Transactions,2021,53(12):1353-1368.
[3] 郭超,陈香玲,郭鹏,等.基于时空A*算法的多AGV无冲突路径规划 [J].计算机系统应用,2022,31(4):360-368.
[4] 李扬.基于冲突搜索的多智能体路径规划算法研究与优化 [D].沈阳:沈阳化工大学,2021.
[5] 宣志玮,毛剑琳,张凯翔.CBS框架下面向复杂地图的低拓展度A*算法 [J].电子学报,2022,50(8):1943-1950.
[6] 官祥锦,陈娟,张为民.基于改进A*算法的多AGV路径规划研究 [J].航空制造技术,2023,66(5):76–85+90.
[7] 周欣慈,朱瑾.基于改进CBS算法的自动化码头多AGV无冲突路径规划 [J].计算机应用研究,2023,40(9):2621-2625+2632.
[8] 陈香玲.电商物流分拣中心多AGV调度与路径规划研究 [D].成都:西南交通大学,2021.
[9] 刘恒麟.多AGV路径规划算法的研究与实现 [D].南京:东南大学,2020.
[10] 张放.极限工况下自动驾驶车辆的轨迹规划与运动控制 [D].北京:清华大学,2018.
[11] 谷万,徐振,郭帅.基于A*和改进动态窗口法的建筑移动机器人路径规划 [J].工业控制计算机,2022,35(8):87-90.
[12] SHARON G,STERN R,FELNER A,et al. Conflict-based search for optimal multi-agent pathfinding [J].Artificial Intelligence,2015,219:40-66.
作者简介:魏胜利(1974—),男,汉族,河南滑县人,副教授,教研室主任,硕士研究生,主要研究方向:计算机控制、智能制造等。