

摘 要:线结构光测量系统具备快速测量和高精度的特点。针对线结构光三维测量系统装置体积较大、扫描范围有限的问题,文章介绍了一种利用单线结构光旋转扫描的三维测量系统,并进行了相关实验验证。首先,基于透视投影线面相交原理,建立了线结构光三维测量模型,完成相机标定以及光平面的标定实验;设计了一种旋转式线结构光的投影模式,并且通过旋转角度对旋转后的光平面进行计算,完成对目标物体的面型测量。实验结果表明,该系统有较高的测量精度,并且可以提高视觉测量系统的便携性。
关键词:三维测量;标定;线结构光;中心线提取
中图分类号:TP391.4 文献标识码:A 文章编号:2096-4706(2024)08-0055-05
DOI:10.19850/j.cnki.2096-4706.2024.08.013
0 引 言
随着“中国制造2025”的推进,人们已经不再依赖于传统的接触式测量,而是更加偏好使用视觉技术[1]来实现目标物面型测量,视觉测量因其非接触、高精度、自动化等特点,在智能制造领域中发挥着关键的作用[2]。
首次提出结构光三维视觉测量方法可追溯到20世纪70年代。其在众多视觉测量方法中占据重要地位[3],这是由于其拥有大量程、较高精度、光条信息容易提取、实时性强和主动受控等特点,因此近年在工业环境中得到了广泛应用。其中,线结构光测量技术是一种结构光三维测量方法,其基本原理是将线状结构光投影到待测物体表面,通过相机接收和记录物体表面调制所产生的光条纹图像畸变,以此实现对物体三维形状的测量[4]。
在线结构光测量中,需要将线结构光投射器或待测目标物安装在可以提供运动的装置上,比如平移台或者旋转台,通过平台的相对运动,才能够对目标物体完成覆盖扫面,以此获得完整的三维形貌数据。目前较为常用的三维测量扫描方式有以下两种:
1)线结构光投射器被固定在平移台上[5],被测目标物体相对静止,投射器随着平移台的移动,按照一定的速率扫描被测物体表面。
2)若线结构光投射器不便于安装在运动平台上,可以将被测物体固定在旋转台上,被测物体随着旋转台按照一定的角度和速率旋转,光条即可完成对目标物体的整体面貌扫描,获得三维信息[6]。
上述两种方式适用于大部分情况,但是第一种方式由于存在平移台等装置,需要较大的运动空间,并且扫描范围有限;在对于尺寸较大且形状复杂的被测工件的测量中,第二种方式存在一定的局限性,无法提供有效测量结果。基于此,本文研究了一种旋转式线结构光测量方法,搭建测量平台,通过投影仪设计一种旋转式的单线结构光投影模式,完成对被测物体的面型测量。
1 基本原理
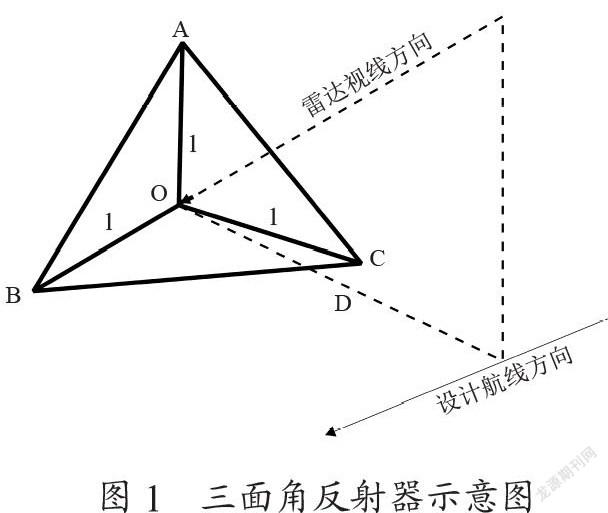
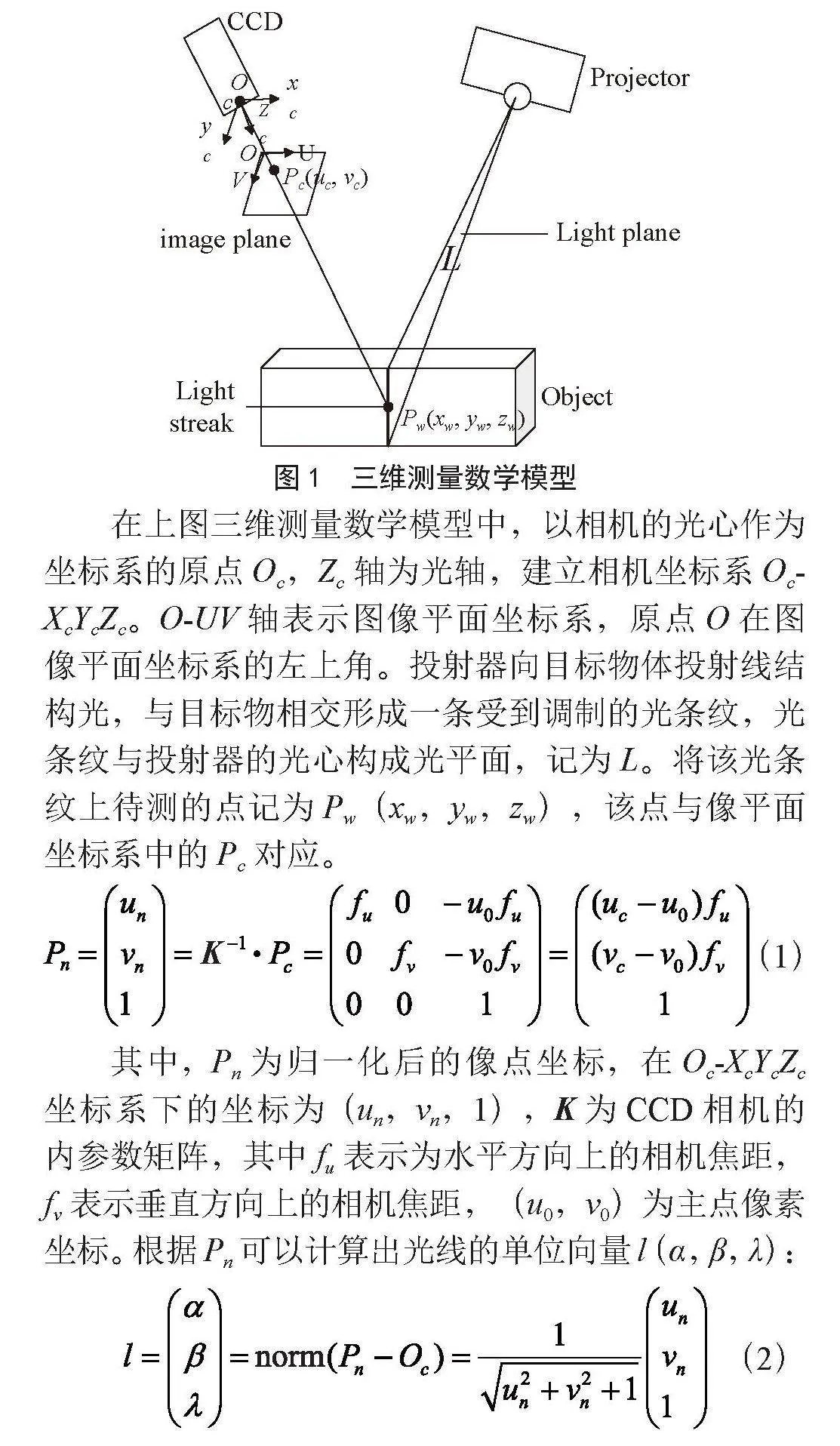
线结构光三维测量系统由相机、投影仪以及计算机构成。通过投影仪投射的光平面与被测物体表面相交,形成一条特征光条,特征光条存在无数个特征点,根据相机模型,特征点在相机图像平面上的坐标可以通过提取光条纹算法得到,并唯一对应空间中一条通过相机光学中心的射线。对相机进行内外参数标定,可以得到射线在三维相机坐标系下的方程[7]。之后通过基于平面约束的标定点提取技术,得到投影仪投射出的光平面在相机坐标系下的方程,已知射线方程和光平面方程,可以唯一确定单线结构光条纹上特征点在相机坐标系下的三维坐标,具体的数学模型如图1所示。
在上图三维测量数学模型中,以相机的光心作为坐标系的原点Oc,Zc轴为光轴,建立相机坐标系Oc-XcYcZc。O-UV轴表示图像平面坐标系,原点O在图像平面坐标系的左上角。投射器向目标物体投射线结构光,与目标物相交形成一条受到调制的光条纹,光条纹与投射器的光心构成光平面,记为L。将该光条纹上待测的点记为Pw(xw,yw,zw),该点与像平面坐标系中的Pc对应。
(1)
其中,Pn为归一化后的像点坐标,在Oc-XcYcZc坐标系下的坐标为(un,vn,1),K为CCD相机的内参数矩阵,其中fu表示为水平方向上的相机焦距,fv表示垂直方向上的相机焦距,(u0,v0)为主点像素坐标。根据Pn可以计算出光线的单位向量l(α,β,λ):
(2)
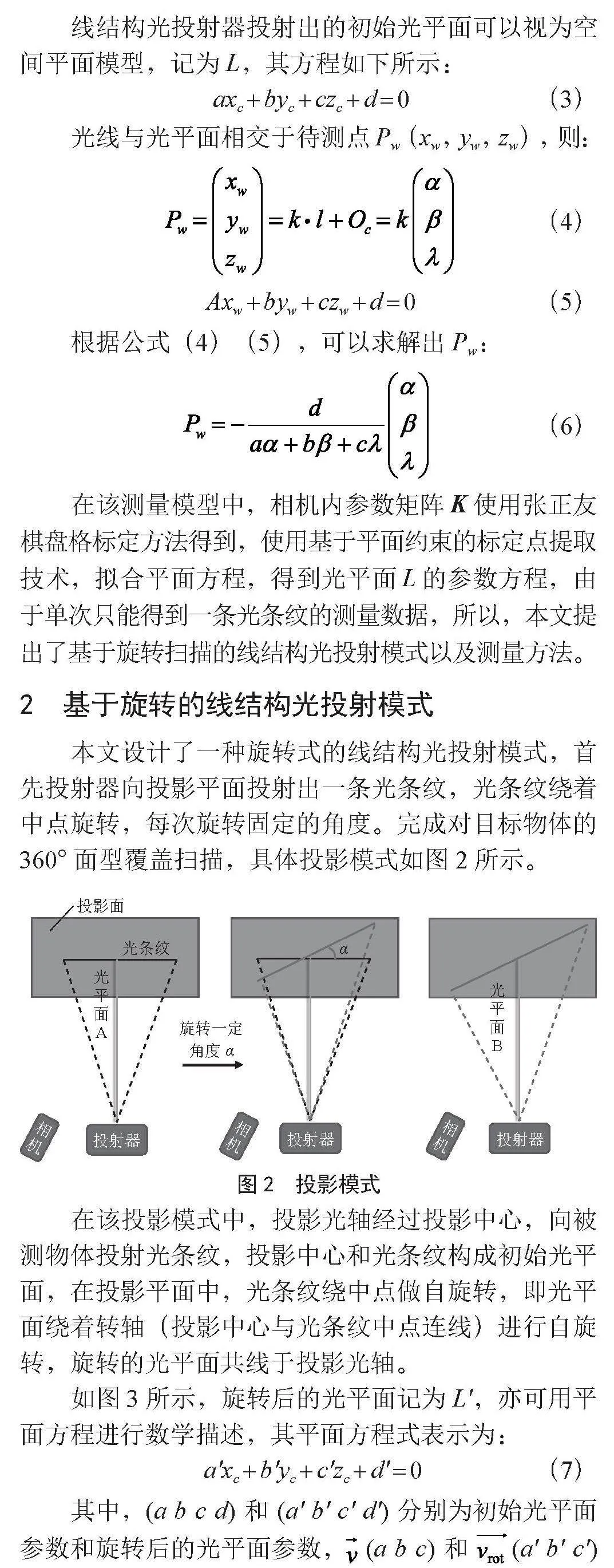
线结构光投射器投射出的初始光平面可以视为空间平面模型,记为L,其方程如下所示:
axc + byc + czc + d = 0 (3)
光线与光平面相交于待测点Pw(xw,yw,zw),则:
(4)
Axw + byw + czw + d = 0 (5)
根据公式(4)(5),可以求解出Pw:
(6)
在该测量模型中,相机内参数矩阵K使用张正友棋盘格标定方法得到,使用基于平面约束的标定点提取技术,拟合平面方程,得到光平面L的参数方程,由于单次只能得到一条光条纹的测量数据,所以,本文提出了基于旋转扫描的线结构光投射模式以及测量方法。
2 基于旋转的线结构光投射模式
本文设计了一种旋转式的线结构光投射模式,首先投射器向投影平面投射出一条光条纹,光条纹绕着中点旋转,每次旋转固定的角度。完成对目标物体的360°面型覆盖扫描,具体投影模式如图2所示。
在该投影模式中,投影光轴经过投影中心,向被测物体投射光条纹,投影中心和光条纹构成初始光平面,在投影平面中,光条纹绕中点做自旋转,即光平面绕着转轴(投影中心与光条纹中点连线)进行自旋转,旋转的光平面共线于投影光轴。
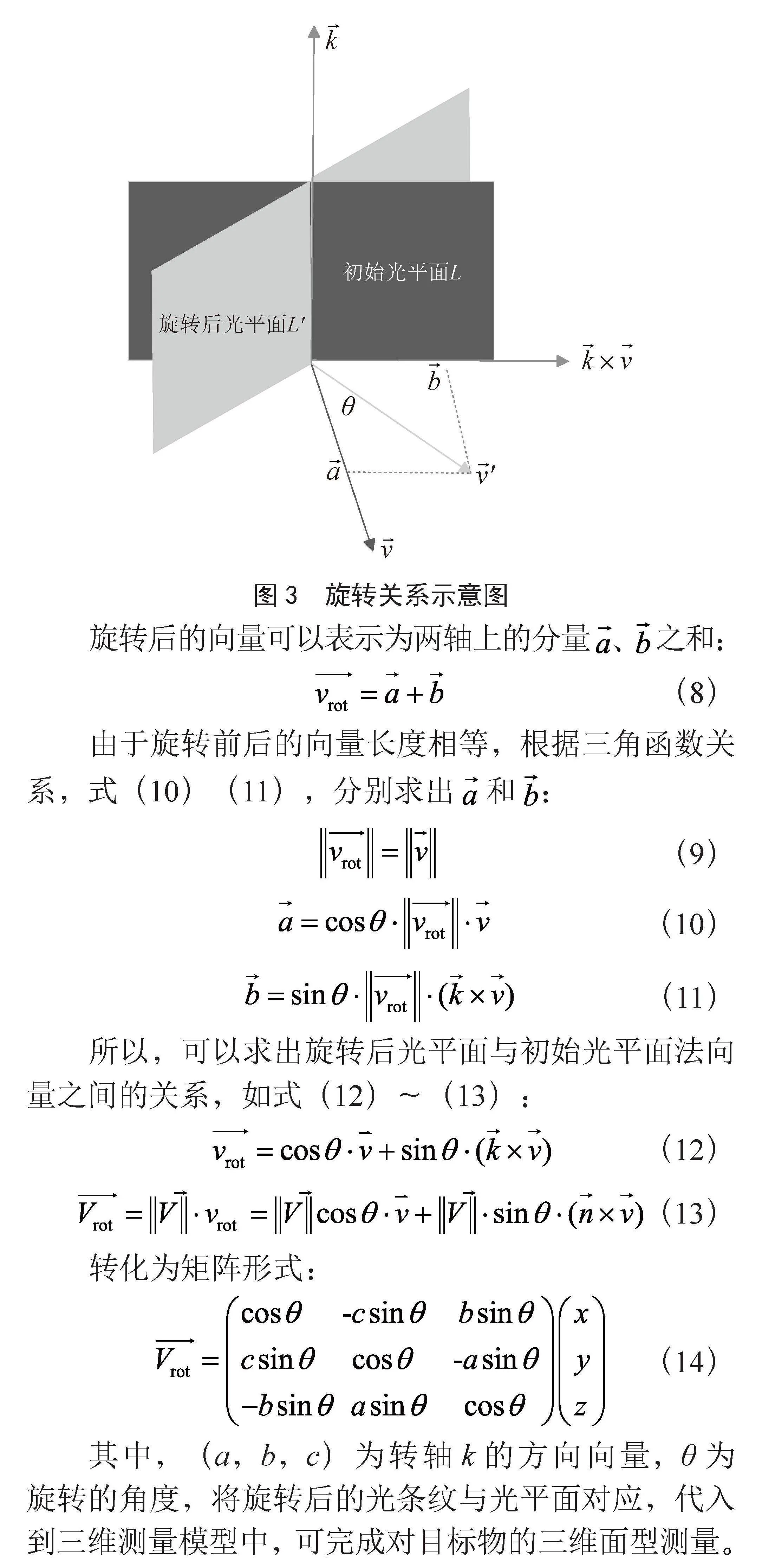
如图3所示,旋转后的光平面记为L′,亦可用平面方程进行数学描述,其平面方程式表示为:
a′xc + b′yc + c′zc + d′ = 0 (7)
其中,(a b c d) 和 (a′ b′ c′ d′) 分别为初始光平面参数和旋转后的光平面参数, (a b c) 和" (a′ b′ c′)为它们平面的法向量。
在图3所示的旋转关系示意图中,旋转轴k使用空间直线方程表示,即使用直线的方向向量" 和在旋转轴上一点进行表示。
旋转后的向量可以表示为两轴上的分量 、 之和:
(8)
由于旋转前后的向量长度相等,根据三角函数关系,式(10)(11),分别求出" 和 :
(9)
(10)
(11)
所以,可以求出旋转后光平面与初始光平面法向量之间的关系,如式(12)~(13):
(12)
(13)
转化为矩阵形式:
(14)
其中,(a,b,c)为转轴k的方向向量,θ为旋转的角度,将旋转后的光条纹与光平面对应,代入到三维测量模型中,可完成对目标物的三维面型测量。
3 实验和数据分析
为了验证所提方法的有效性,搭建三维测量系统,并在三维测量前进行系统标定,主要包括相机参数标定实验、初始光平面标定实验、以及旋转轴标定实验三部分,最后完成三维测量实验。
3.1 相机标定实验
相机参数标定实验是为了获取前文提到的fu、fv、u0、v0等参数。本文采用张正友相机标定方法[8],利用MATLAB中的工具箱对相机参数进行标定。平面靶标采用12×9、间隔20 mm的棋盘格作为,选择与测量位置等距离下的不同位置放置平面靶标并采集图像,使平面靶标覆盖在相机的整个视野下,共采集15张图像,如图4所示,最后五张靶标图为光平面标定实验获取旋转,平移参数所用,具体见下一节。
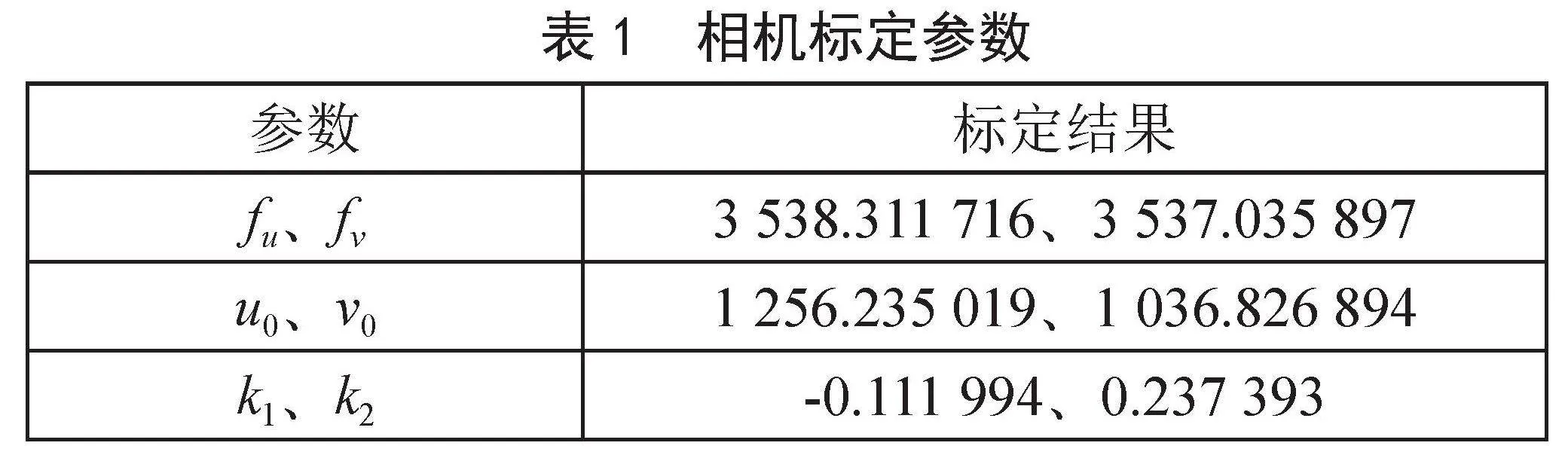
将提取出的平面靶标角点坐标导入张正友标定算法,得到的相机参数如表1所示。
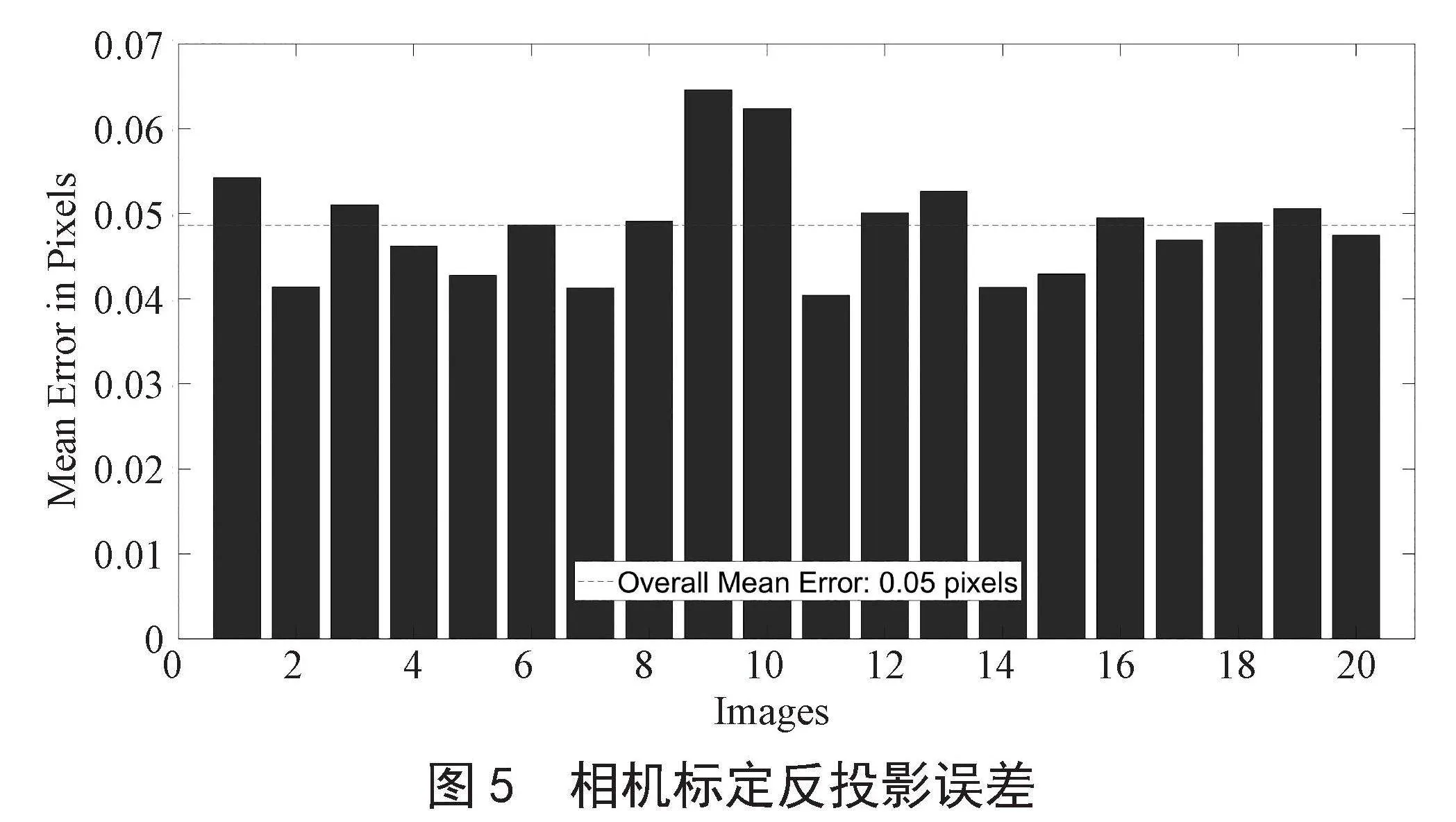
表中,fu、fv分别表示为相机水平和垂直方向上的焦距,u0、v0表示为主点像素坐标,k1、k2为相机径向畸变参数。为了评估相机参数标定的精度,通过已知棋盘格上角点在世界坐标系下的坐标计算出像素坐标,再通过内参矩阵和外参矩阵反投影回相机坐标系下,最后与实际的世界坐标求差,即可得到相机标定的反投影误差,如图5所示,最大误差0.067 8 pixel,平均误差为0.049 2 pixel。
3.2 光平面标定实验
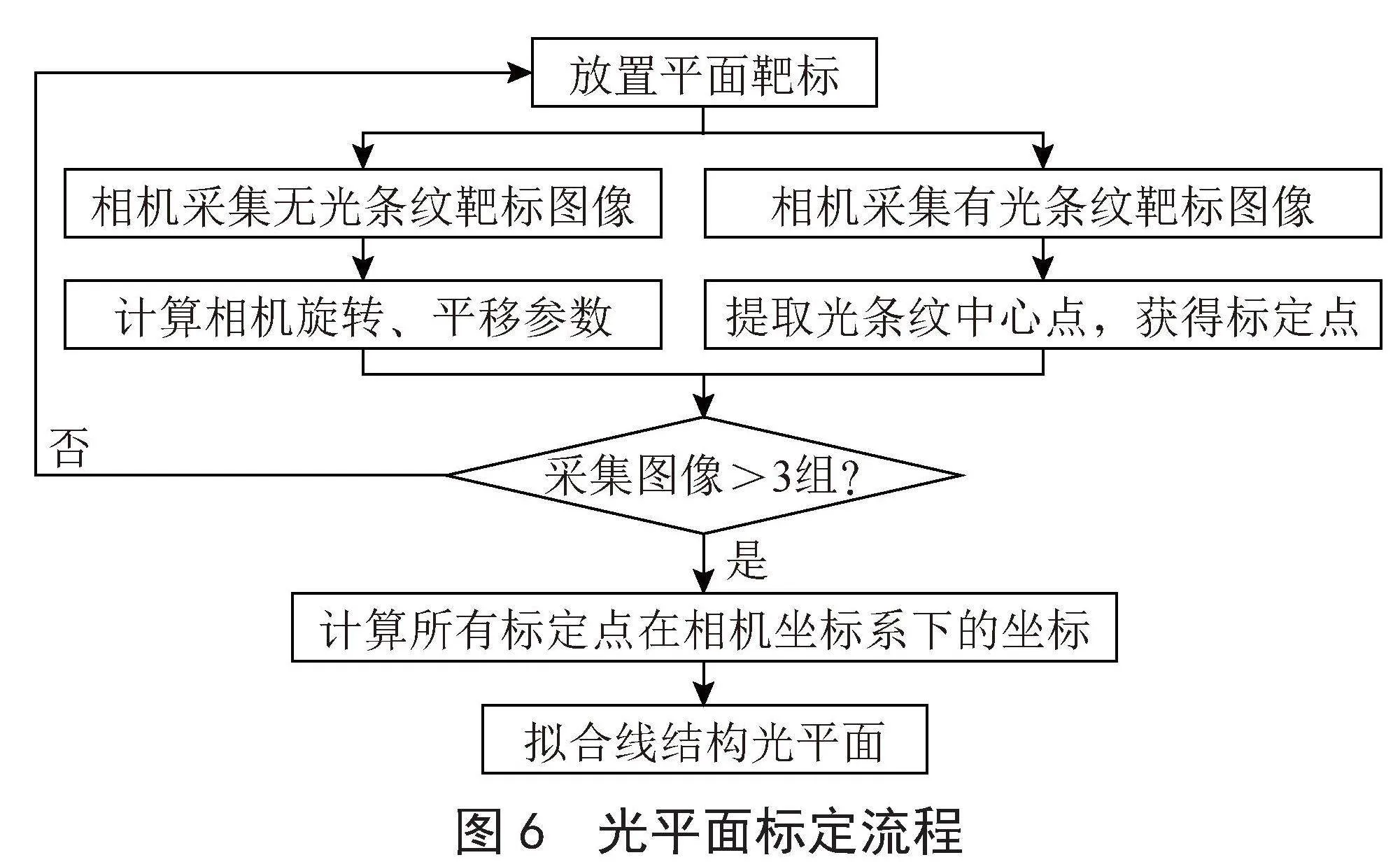
线结构光平面可以视为空间平面,在三维空间中,三个彼此不共线的三维点可以确定一个平面,基于此,采用基于平面约束的光平面标定算法[9],提取到大量的非共线标定点在相机坐标系下的三维坐标值,拟合光平面方程,图6为基于平面约束的光平面标定方法的实验流程。
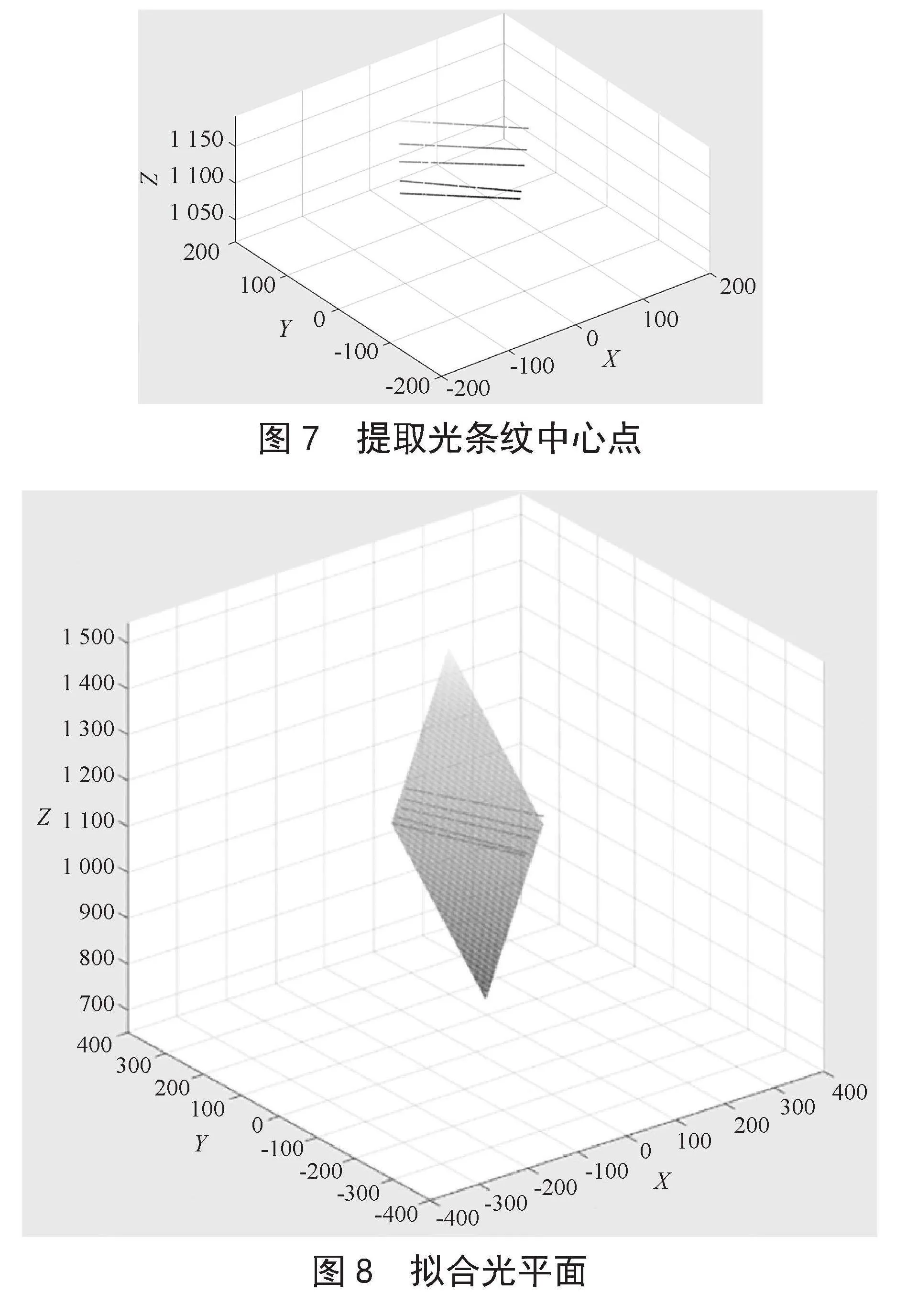
分别采集不带光条纹靶标图像和带有光条纹的靶标图像,之后对采集的图像进行畸变矫正。无光条纹图像通过相机标定方法计算出旋转矩阵以及平移向量;带有光条纹的靶标图像用来获得标定点,使用灰度重心法提取光条纹中心点[10],根据对应的相机外参数将标定点转化为相机坐标系下的坐标;改变标定板位置,重复上述操作五次,将所有的标定点的坐标统一在相机坐标系下,如图7所示,最后拟合出线结构光平面[11],如图8所示。
所得到的初始光平面参数如表2所示。
3.3 旋转轴标定
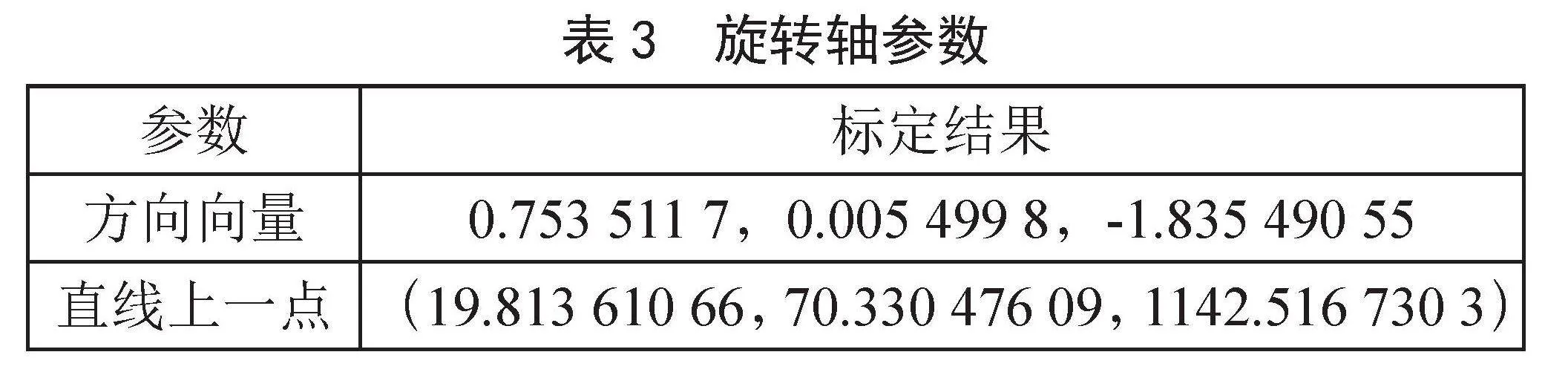
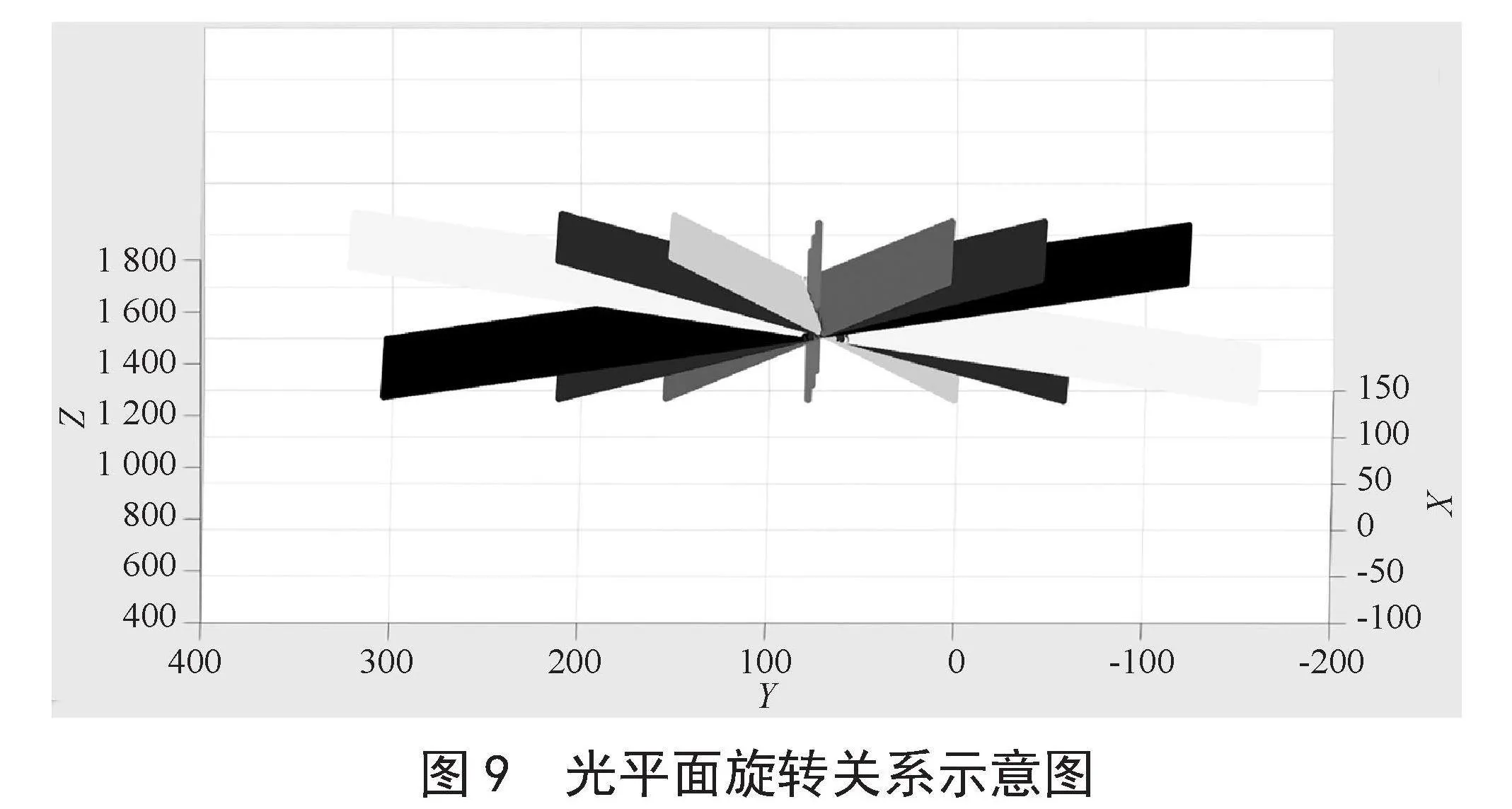
在本文提出的旋转式三维测量系统中,旋转轴k使用直线的方向向量和位于直线上一点进行表示。通过多次光平面标定得到具有旋转关系的7个光平面方程,它们相交于旋转轴,如图9所示。
求解出七个光平面方程线性方程组,得到相交直线的方向向量;向二维靶标多次投射旋转关系的线结构光,并且使用非线性优化算法,得出一点距离n条光条纹的距离之和最小,得到旋转轴上的一点,具体参数如表3所示。
3.4 三维测量实验
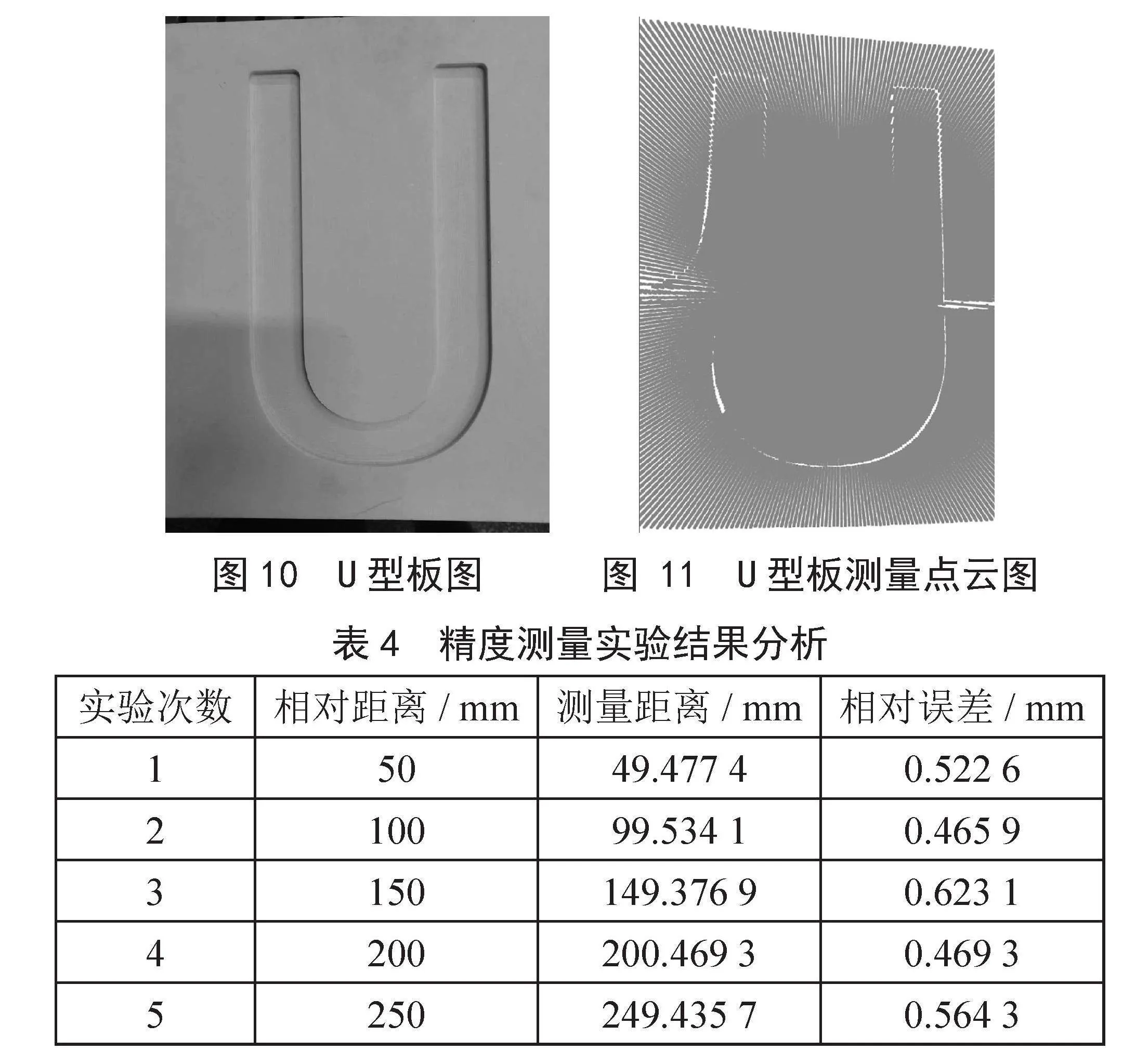
选择U型板作为被测物体,如图10所示,U型板高300 mm,宽300 mm,放置于距离测量系统1 200 mm视场下,使用投影仪向目标物投射旋转式线结构光,设定单次逆时针旋转1°,线结构光被U型板所调制,相机采集线结构光图像,并且传输至计算机中,采用灰度重心法提取光条纹中心点坐标,根据上述得到的标定结果,一同代入到三维测量模型中,计算得到U型板点云数据,如图11所示,可以看出,点云数据基本上的反映出了U型板的面型特征。
为了进一步分析测量系统的稳定性与可靠性,将一白板固定在平移台上,白板尺寸与U型板相同,白板首先在距离测量系统1 200 mm位置处进行测量,平移台控制白板向前移动,每次移动50 mm,进行5次测量,通过白板前后移动的实际相对距离与测量距离进行对比,分析出该系统的测量误差,具体如表4所示,结果证明,该三维测量系统的平均测量误差为0.529 04 mm。
4 结 论
针对线结构光扫描装置体积较大,扫描范围有限的问题,本文提出了一种旋转式线结构光的三维测量系统,该系统仅需要投影仪和相机即可完成对目标物体的三维测量。在测量之前,需要预先标定出相机参数,初始光平面参数以及旋转轴参数,再通过旋转矩阵对旋转后的光平面进行计算,完成点云的拼接组合。通过实验表明,该系统对目标物量有较好的测量效果,可以很好的显示出被测物体的面型特征,为线结构光三维测量提供了新思路。
参考文献:
[1] 张宗华,刘巍,刘国栋,等.三维视觉测量技术及应用进展 [J].中国图象图形学报,2021,26(6):1483-1502.
[2] 吴腾飞.视觉测量图像处理关键算法的研究和应用 [D].天津:天津大学,2010.
[3] 左超,张晓磊,胡岩,等.3D真的来了吗?——三维结构光传感器漫谈 [J].红外与激光工程,2020,49(3):9-53.
[4] 余石鹏.基于线结构光测量系统的齿轮测量误差与测量不确定度研究 [D].赣州:江西理工大学,2022.
[5] 王斌,张文清,王众,等.基于线结构光扫描的结冰冰形三维测量 [J].测控技术,2022,41(12):66-71+77.
[6] 梁莹智.基于线激光旋转扫描的三维快速测量系统 [D].杭州:浙江大学,2021.
[7] 余乐文,张达,张元生.基于线结构光的三维测量系统关键技术研究 [J].光电子·激光,2016,27(2):156-161.
[8] 迟德霞,王洋,宁立群,等.张正友法的摄像机标定试验 [J].中国农机化学报,2015,36(2):287-289+337.
[9] 余成义.基于线激光转镜扫描的机器人视觉检测技术研究 [D].上海:上海交通大学,2017.
[10] 李莹莹,张志毅,袁林.线结构光光条中心提取综述 [J].激光与光电子学进展,2013,50(10):13-22.
[11] 于龙龙,李艳文,栾英宝,等.基于二维平面靶标的线结构光标定 [J].仪器仪表学报,2020,41(6):124-131.
作者简介:冯宁(1999—),男,汉族,河南郑州人,硕士研究生在读,研究方向:数字图像处理、机器视觉;佟星(1998—),男,汉族,河南商丘人,硕士研究生在读,研究方向:数字图像处理、计算机视觉。
收稿日期:2023-09-08
Research on Three-dimensional Measurement Method Based on Single-line Structured Light
FENG Ning, TONG Xing
(North China University of Water Resources and Electric Power, Zhengzhou 450046, China)
Abstract: Line structured light measurement system has the characteristics of fast measurement and high accuracy. Aiming at the problems of large size and limited scanning range of line structured light 3D measurement system, this paper introduces a 3D measurement system using single-line structured light for rotational scanning, and carries out relevant experiments to verify it. First of all, based on the principle of intersection of perspective projection lines and surfaces, a three-dimensional measurement model of line structured light is established to complete the camera calibration as well as the calibration experiments of the optical plane. A projection mode of rotating line structured light is designed, and the calculation of the rotated optical plane is carried out through the rotation angle, so as to complete the measurement of the face shape of the target object. The experimental results show that the system has high measurement accuracy and can improve the portability of the visual measurement system.
Keywords: 3D measurement; calibration; line structured light; centerline extraction