
摘 要:对城市配送路线的设计进行了研究,在复杂的城市道路选择上,首先采用Dijsktra算法求解单源最短可行性路径,从而得到配送中心到客户以及客户到客户之间的物流配送网络;其次运用粒子群算法的自适应性和鲁棒性,设计出城市配送路线优化方案;最后将优化后的配送效果与原来的配送计划进行对比分析,发现优化后的路径更短,效果更优,可为解决城市配送问题提供实际参考。
关键词:路径优化;Dijsktra算法;粒子群算法
中图分类号:TP18;F252 文献标识码:A 文章编号:2096-4706(2024)08-0156-06
DOI:10.19850/j.cnki.2096-4706.2024.08.034
收稿日期:2023-09-12
基金项目:江苏省高等教育教改研究立项课题项目(2019JSJG367);江苏高校“青蓝工程”
0 引 言
相比较于长距离的运输,城市配送的交通道路四通八达,可选择性路径的数量更多,在每一次交通道路交叉点就面临一次线路选择,而每一次选择的不同,构成的路径就不同,因此,配送路线的选择更加复杂。车辆路径问题(Vehicle Routing Problem, VRP)是运筹学领域研究的热点问题之一,由Dantzing等人于1959年首先提出来[1],是配送优化中的关键问题,也是组合优化问题中经典的NP难题[2]。
在车辆路径问题的求解方法上,目前学者们展开了丰富的研究。张莉[3]采用粒子群算法中的学习因子优化技术,设定船只调度计算模块,完成海上物流智能配送系统的设计工作;刘娜翠等[4]通过使用改进的遗传算法求解以费用最小为目的的带时间窗的整车物流配送问题;杨倩等[5]认为改进粒子群算法的解优于自适应粒子群算法且运行时间短;明小菊等[6]认为利用莱维飞行和反向学习对粒子群算法进行优化用于模型求解;李董洁等[7]认为整车运输问题可以分为两段模型进行求解,长距离跨省运输采用Dijsktra算法进行求解,对于整车短距离省内运输可以采用改进粒子群算法以成本最小为模型进行求解。
本文在满足需求点配送辆和配送时间要求的前提下,以配送距离最短为模型目标,利用Dijsktra算法和粒子群算法相结合的方法求解最优配送方案,以期为城市物流配送的优化提供参考。
1 VRP模型假设和参数描述
1.1 VRP模型假设
为了提高研究的效率和实用性,提出以下假设:
1)配送中心能够满足所有客户的需求量。
2)配送中心的车辆的容量、型号、运量都已知,且每辆车在装载过程中都不会超载,中途不会出现抛锚现象,不会超过当天车辆的最大里程数。
3)每个客户的货物需求量和需求时间均为已知。
4)假设车辆不论是什么路段,均采用匀速行驶,不同路段的速度根据拥堵情况根据拥堵指数呈倍数关系。
5)假设操作工的单位货物卸载速度不变,卸货时间与货物量呈正比的线性关系。
6)假设客户需要的货物在装车的过程中可以进行混装。
7)假设每个客户每日只能由一个配送车辆为其送货,但每个配送车辆可以配送多个客户。
1.2 模型相关参数的描述
根据本文需要,相关参数所示的意义如下:
C表示总的运输距离;dij表示运输车辆在客户i点至客户j点之间的距离,当i = 0时,表示配送中心;I = {i i = 0,1,2,3,…,n}表示配送点集合,i = 0时,表示的含义是配送中心;K = {k k = 0,1,2,3,…,m}表示可选择的车辆的集合;m表示车辆总数;n表示客户总数;Qj表示表示配送点j的运载量; 表示第k辆车从配送中心到客户j的运输时间;Mk表示第k辆车的最大载重量; 表示第k辆车到达客户i后卸货花费的作业时间;Tij表示配送车辆从客户i到客户j花费的货运时间;[ei,li] (i = 1,2,3,…,n)表示配送中心与客户i预先定好的送货时间窗。
2 VRP模型目标函数的构建
2.1 VRP目标函数的构建
本文基于对城市物流配送问题的分析,根据南通大数据显示,南通交通的拥堵现状依旧位列文明交通畅通城市前三名,因此在文章的模型构建中基本可以忽略南通城市拥堵因素对路径优化的影响,所以将物流配送距离作为目标,构建目标函数。目标函数算式为:
(1)
2.2 VRP约束条件构建
根据配送目标为配送距离最小化,本文所建立模型的约束条件包括车辆、客户和配送时间窗,具体表现如下。
2.2.1 车辆的约束
1)公司每辆车都参与配送:
(2)
2)每辆车的实际货物载重量小于车辆最大载重量:
(3)
3)所有车辆的总运输量大于所有客户的总运输量:
(4)
2.2.2 客户的约束
1)所有的客户需求均被满足:
(5)
2)每一个客户配送过程由唯一车辆提供服务:
(6)
2.2.3 配送时间窗的约束
1)每个客户的配送时间都在时间窗允许的范围内:
(7)
2)到达客户点的时间由到达前一个客户的时间,加上前一个客户的卸货时间和车辆在客户之间的运输时间:
(8)
3 案例介绍
3.1 企业案例介绍
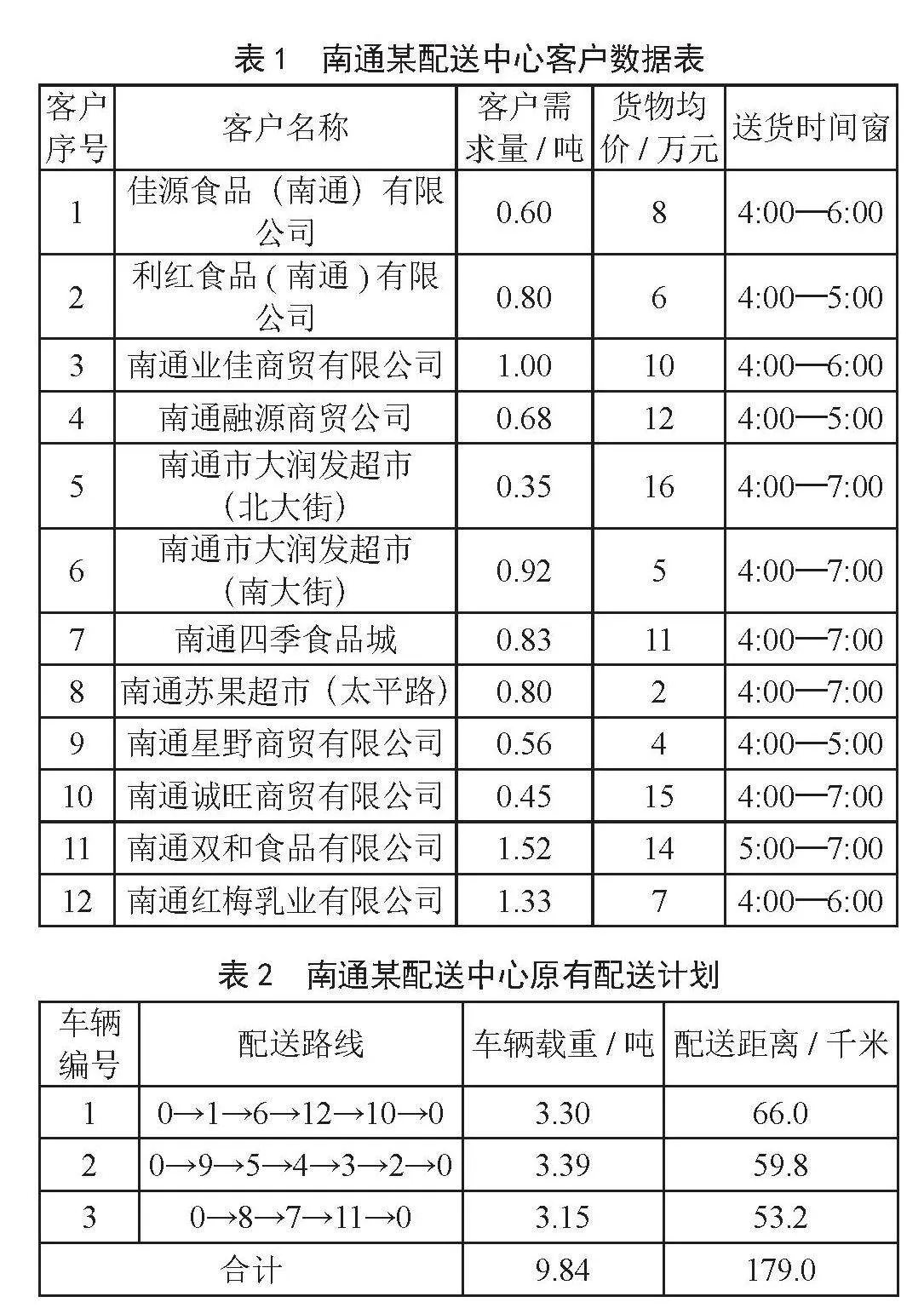
本文研究区域主要为南通市的主城区,以企业配送中心为起点,对客户进行每日配送。通过前期实践调研发现,在日常的配送安排中,调度员会根据各个客户的地理位置对其进行区域划分,再根据各个点的需求量将每辆车辆发货任务安排好了之后,货车司机根据被安排到的客户,由地图多个目的地进行导航,或者是按照自身经验来进行配送。实际上,由于客户的每日要货需求变化不大,在调度安排和路线选择时变化也不是特别大。数据收集包括门店信息、客户需求量、货物均价、送货时间窗以及配送点之间的可行路径数据,如表1所示。
3.2 企业配送现状
在日常配送中,配送路线计划主要是根据驾驶员的配送经验或是TMS手机APP软件或是导航地图推荐来安排具体工作的,这样的线路安排在某种程度上是十分合理的,但却不是我们要寻求的最短配送路径。通过实地走访调研,获得原始的配送方案,如表2所示,其中0表示配送中心,数字1~12指每一个客户点。
4 VRP模型求解企业案例
4.1 Dijkstra算法求解最短距离
4.1.1 基本思想
Dijkstra算法采用的是一种贪心的策略,解决的是有权图中单源最短路径问题[8],基本思想可以表述为,在一个图G = (V,E)中,有n个点,边上的权重记为两点距离,计算过程以起始点为中心向外层层扩展求解距离起点的最短路径,直到扩展到终点为止。计算方法一般有两种方式,一种是标号法,一种是用OPEN、CLOSE表的方式。
4.1.2 可行路径网络构建
文章研究的是城市配送,城市道路错综复杂、四通八达,可选择通行的道路有很多,配送点之间的可通行路径并不唯一。因此,为解决点到点的最短路径问题可以采用构建可行性路径网络的方式,在此基础上,相较于采用坐标计算的方式确定两点之间的距离,文章采用地图推荐路线的方式,在地图中输入地点名称,选择驾车搜索方式,地图中会推荐多条可选择性路径,根据推荐的多条路线规划的方式在实践中可操作性更强一些,计算出的结果更加符合实际。
4.1.3 物流配送网络构造
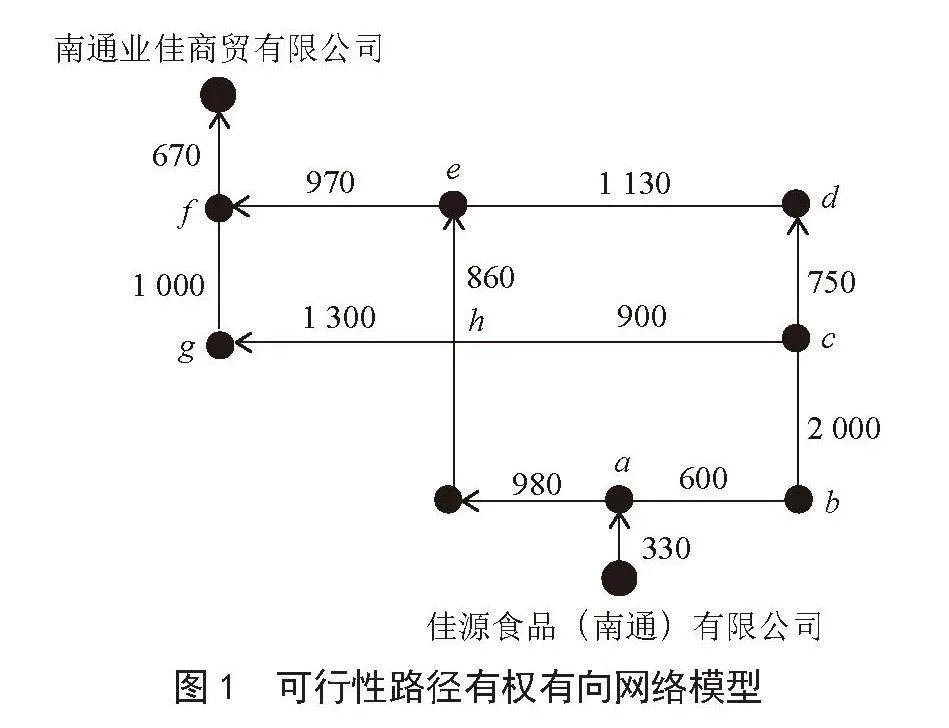
根据地图的搜索结果,将可行性路径抽象为网络模型,可以直接得到无权有向可行路径网络,但这还无法直接计算出两点之间的最短路径,需要进一步计算得出连接点之间的距离,即对每条边赋予权值。根据经验,本文运用了地图的测距工具获取每条路段的地理距离,以佳源食品(南通)有限公司到南通业佳商贸有限为例,如图1所示,距离单位为米。
4.1.4 Dijkstra算法求解步骤
运用Dijsktra算法计算从佳源食品(南通)有限公司到南通业佳商贸有限公司的可行性网络之间的最短距离,本文在计算过程中主要采用标号法进行计算,具体计算步骤如下:
1)首先给佳源食品(南通)有限公司以P标号。P佳= 0,X = {佳源食品(南通)有限公司}。
2)min{d佳a} = min{0 + 330} = 330,X = {佳源食品(南通)有限公司,a},pa = 330。
3)min{dai,dab} = {330 + 980,330 + 600}={1 310,930} = 930,X = {佳源食品(南通)有限公司,a,b},pb = 930。
4)min{dai,dbc} = min{330 + 980,930 + 2 000} = min{1 310,2 930} = 1 310,X = {佳源食品(南通)有限公司,a,b,i},Pi = 1 310。
5)min{dih,dbc} = min{1 310 + 3 140,930 + 2 000} = min{4 450,2 930} = 2 930,X = {佳源食品(南通)有限公司,a,b,i,c},pc = 2 930。
6)min{dch,dcd,dih} = {2 930 + 900,2 930 + 750,1 310 + 3 140} = min{3 830,3 680,4 450} = 3 680,X = {佳源食品(南通)有限公司,a,b,i,c,d},pd = 2 930。
7)min{dch,dih,dde} = {2 930 + 900,1 310 + 3 140,3 680 + 1 130} = min{3 830,4 450,4 810} = 3 830,X = {佳源食品(南通)有限公司,a,b,i,c,d,h},ph = 3 830。
8)min{dhg,dhe,dde} = {3 830 + 1 300,3 830 + 860,3 680 + 1 130} = min{5 130,4 690,4 810} = 4 690,X = {佳源食品(南通)有限公司,a,b,i,c,d,h,e},pe = 4 690。
9)min{dhg,def} = min{3 830 + 1 300,4 690 + 970} = min{5 130,5 660} = 5 130,X = {佳源食品(南通)有限公司,a,b,i,c,d,h,e,g},pg = 5 130。
10)min{dgf,def} = min{5 130 + 1 000,4 690 + 970} = min{6 130,5 660} = 5 660,X = {佳源食品(南通)有限公司,a,b,i,c,d,h,e,g,f},pf = 5 660。
11)min{df南} = min{5 660 + 670} = 6 330,X = {佳源食品(南通)有限公司,a,b,i,c,d,h,e,g,f,南通业佳商贸有限公司},p南 = 6 330。
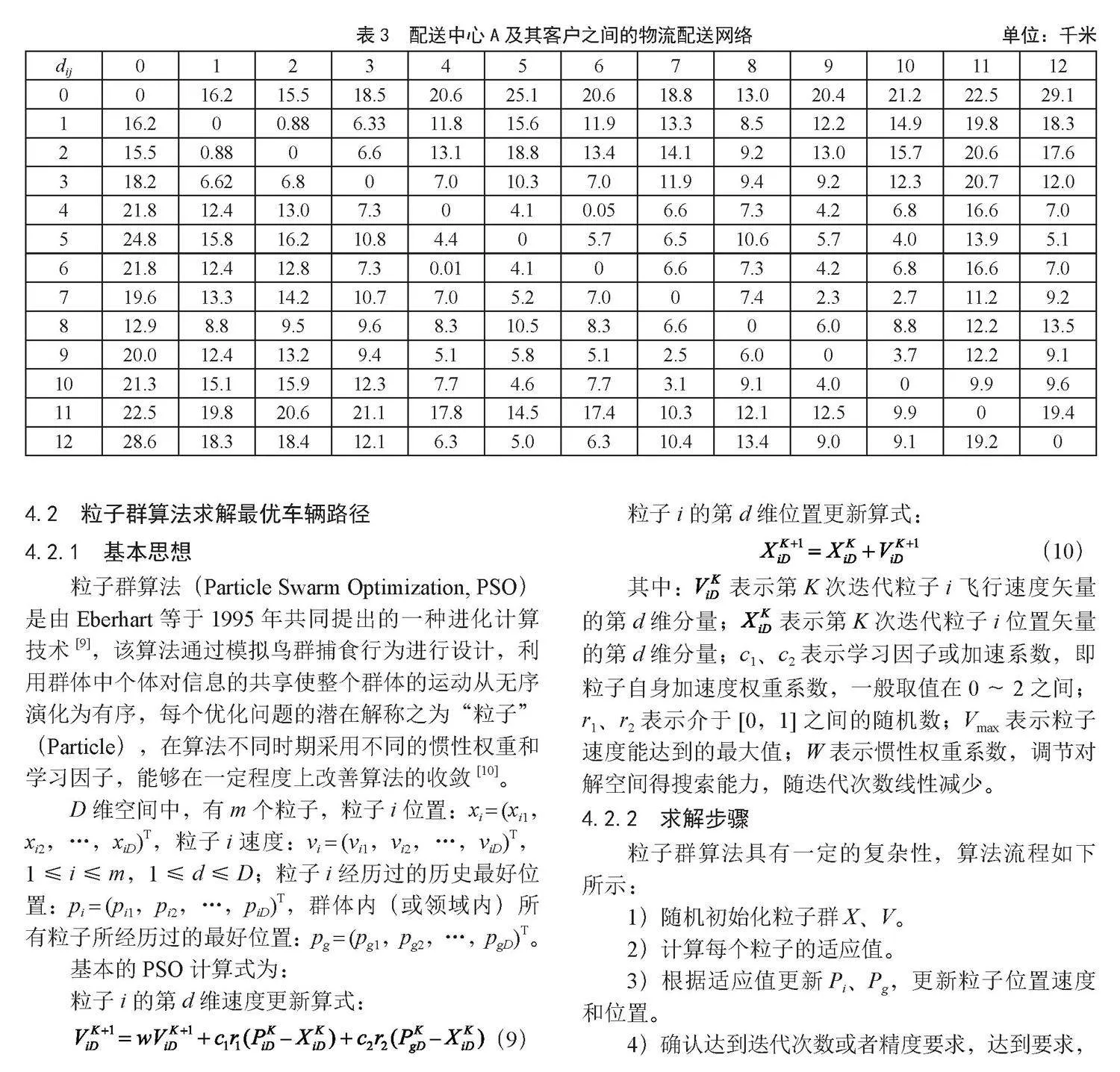
通过计算,可以得出p南 = 6 330。因此,从佳源食品(南通)有限公司到南通业佳商贸有限公司的可行性网络之间的最短距离为6.33千米,路径为佳源食品(南通)有限公司→ a → b → c → h → e → f →南通业佳商贸有限公司。这条路径在地图线路推荐和最短路径中并未显示,但却是最短距离。对本文13个点每两个点组成的156条路径运用Dijsktra算法筛选出两两点之间的唯一路径,因数据较多,本文采用Dijsktra代码的方法计算结果,构成一个物流配送网络,如表3所示。
4.2 粒子群算法求解最优车辆路径
4.2.1 基本思想
粒子群算法(Particle Swarm Optimization, PSO)是由Eberhart等于1995年共同提出的一种进化计算技术[9],该算法通过模拟鸟群捕食行为进行设计,利用群体中个体对信息的共享使整个群体的运动从无序演化为有序,每个优化问题的潜在解称之为“粒子”(Particle),在算法不同时期采用不同的惯性权重和学习因子,能够在一定程度上改善算法的收敛[10]。
D维空间中,有m个粒子,粒子i位置:xi = (xi1,xi2,…,xiD)T,粒子i速度:vi = (vi1,vi2,…,viD)T,1≤i≤m,1≤d≤D;粒子i经历过的历史最好位置:pi = (pi1,pi2,…,piD)T,群体内(或领域内)所有粒子所经历过的最好位置:pg = (pg1,pg2,…,pgD)T。
基本的PSO计算式为:
粒子i的第d维速度更新算式:
(9)
粒子i的第d维位置更新算式:
(10)
其中: 表示第K次迭代粒子i飞行速度矢量的第d维分量; 表示第K次迭代粒子i位置矢量的第d维分量;c1、c2表示学习因子或加速系数,即粒子自身加速度权重系数,一般取值在0~2之间;r1、r2表示介于[0,1]之间的随机数;Vmax表示粒子速度能达到的最大值;W表示惯性权重系数,调节对解空间得搜索能力,随迭代次数线性减少。
4.2.2 求解步骤
粒子群算法具有一定的复杂性,算法流程如下所示:
1)随机初始化粒子群X、V。
2)计算每个粒子的适应值。
3)根据适应值更新Pi、Pg,更新粒子位置速度和位置。
4)确认达到迭代次数或者精度要求,达到要求,转至5),若没有达到要求,返回至2)。
5)输出所需参数。
4.2.3 参数设置与分析
根据粒子群算法的描述和已有的研究成果,粒子群算法的模型中,主要有以下参数变量:惯性权值w,加速因子c1、c2,种群数N,迭代次数Loop_max,粒子维数D。本文的参数设置如下:
1)惯性权重w的大小决定了粒子在多大程度上保留了原来的速度,w值设置的过大或过小,都会影响到算法在求解时收敛能力。本文将w的值设置为0.729,并将其运用到粒子位置更新的幅度。
2)加速因子c1和c2分别用于控制指向自身或邻域最佳位置的运动,一般取值在0~4,两者的和小于等于4。本文取c1 = c2 = 1.494 45,用于计算粒子位置更新的速度。
3)种群规模N的设置,根据经验,种群规模太小则通常不能提供足够的采样点,容易导致算法性能较差,难以获取最优解;可是,如果种群规模过大,势必会增加整体计算量,从而导致收敛时间过长,即收敛速度缓慢。本文根据实际情况将N设置为12用于求解最优路径。
4)迭代次数Loop_max的大小决定了解的收敛,太小解值不太稳定,太大计算浪费时间,本文将Loop_max设置为50。
5)粒子维数D取决于有待优化函数的维数,即粒子群中粒子的个数,本文取1 000。
4.2.4 算法实现
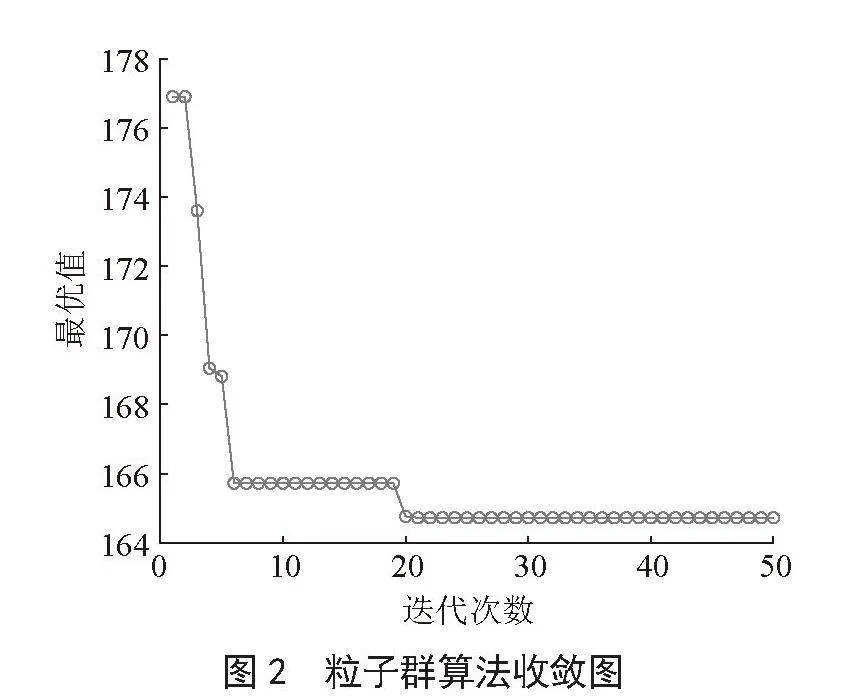
本文选择MATLAB软件进行配送路径优化工作,得出粒子群算法收敛图如图2所示,其中横坐标表示迭代次数,纵坐标表示路径长度。
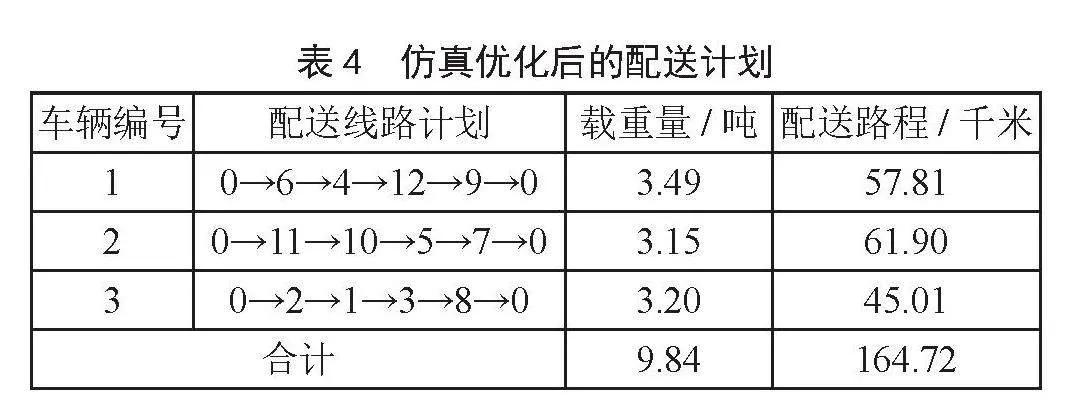
本次算法在第20次迭代中趋于稳定,数值稳定在164.72千米,具体粒子群算法结果如表4所示,其中0表示南通某配送中心,数字1~12指每一个客户点。
4.3 优化结果分析
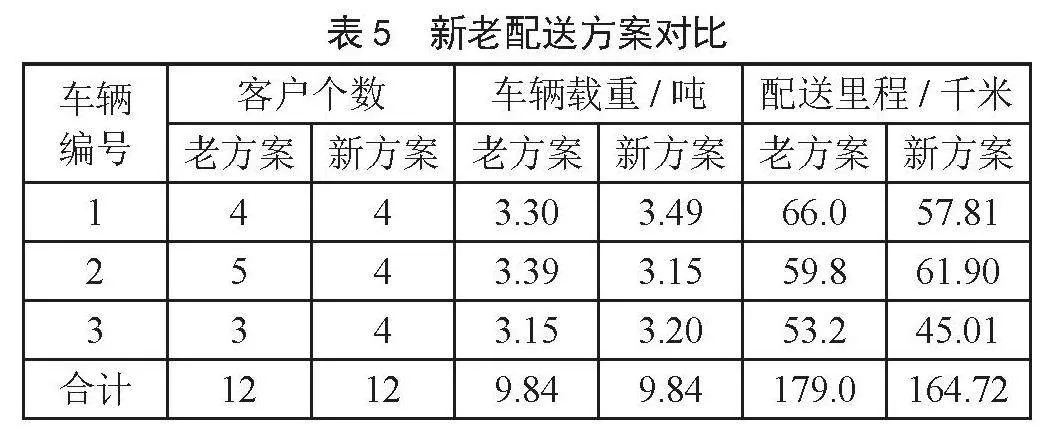
用MATLAB仿真软件优化得出的优化后新配送方案中,新计划中依然使用3辆冷藏运输车,每辆车的总载重量都在额定载重3.5吨以下。从每辆车分配客户的个数上看,新方案中车辆分配的客户个数比老方案总个数更均匀,每辆车的配送客户数量和货物载重相对一致,较之前的配送方案,不会产生因为某辆车配送客户较多而开关门的次数较多的现象,减少了货损机会;从车辆载重的对比分析可得,新老方案车辆都没有超载,货量分配相对都相对比较均匀,能够满足客户需求;从每辆车的配送里程对比发现,新方案中总的配送路程为164.72千米,比原来方案中配送里程179千米缩短了14.28千米,在城市小范围的配送中具有一定的效果,如表5所示。
5 结 论
文章在满足需求点的配送量和配送时间窗的前提下,以最短配送距离为目标构建城市配送路线优化模型,运用Dijkstra算法和粒子群算法相结合的求解方法设计了城市配送路线,结果表明,优化后的配送方案效果更优,验证了Dijkstra算法和粒子群算法在解决配送路径优化问题的价值,所得研究成果能够帮助企业在城市配送中合理安排配送方案,有效降低企业成本。然而,文章在研究配送路线方案时未考虑交通堵塞、单行道问题以及客户对配送时间先后顺序的要求,后续研究中将尽可能地考虑一些可能性因素对模型的影响,从而提升模型的适应度。
参考文献:
[1] DANTZIG G B,RAMSER J H. The Truck Dispatching Problem [J].Management Science,1959,6(1):80-91.
[2] 杨笑笑,柯琳,陈智斌.深度强化学习求解车辆路径问题的研究综述 [J].计算机工程与应用,2023,59(5):1-13.
[3] 张莉.基于粒子群算法的海上物流智能配送系统 [J].舰船科学技术,2020,42(10):196-198.
[4] 刘娜翠,张兰怡,杨映艳,等.基于遗传算法的汽车整车销售物流配送路径优化 [J].数学的实践与认识,2021,51(7):35-42.
[5] 杨倩,陈再良.基于改进粒子群算法的车间物料配送方法研究 [J].机械设计与制造,2022(8):238-241.
[6] 明小菊,珠兰.城市生鲜食品冷链物流配送路径优化技术研究 [J].包装与食品机械,2022,40(2):76-81.
[7] 李董洁,梁革英.整车智能调度运输研究 [J].物流工程与管理,2022,44(2):103-109.
[8] 张亚东,李起宏,陆涛涛,等.基于多源迪杰斯特拉搜索和拥塞协商的详细布线 [J].中国集成电路,2022,31(4):53-58+63.
[9] EBERHART R C,SHI Y. Comparing inertia weights and constriction factors in particle swarm optimization [C].Proceedings of the 2000 Congress on Evolutionary Computation.La Jolla:IEEE,2000:84-88.
[10] 王翼虎,王思明.基于改进粒子群算法的无人机路径规划 [J].计算机工程与科学,2020,42(9):1690-1696.
作者简介:孙红冉(1989—),女,汉族,江苏徐州人,经济师、实验师,硕士,研究方向:物流工程、物流实践教学;施彦(1984—),男,汉族,江苏南通人,经济师、高级实验师,硕士,研究方向:物流工程。
Research on Urban Delivery Path Optimization Problem Based on Dijsktra-PSO Algorithm
SUN Hongran, SHI Yan
(Jiangsu Vocational College of Business, Nantong 226011, China)
Abstract: A study is conducted on the design of urban delivery paths. In the selection of complex urban roads, the Dijsktra algorithm is first used to solve the shortest feasible path of a single source, thereby obtaining the logistics delivery network from the delivery center to customers and from customers to customers. Secondly, it designs an optimization plan for urban delivery paths using the adaptability and robustness of particle swarm optimization. Finally, the optimized delivery effect is compared with that of the original delivery plan, and it is found that the optimized path is shorter and the effect is better, which can provide practical reference for solving urban delivery problems.
Keywords: path optimization; Dijsktra algorithm; Particle Swarm Optimization