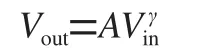

摘 要:针对传统图像去雾方法去雾效果有限、存在光晕效应、色彩失真等不足,文章提出一种结合Al-Alaoui算子的改进暗通道先验去雾算法。算法首先用Al-Alaoui算子对图像做卷积滤波增强处理,再用改进的四叉树搜索方法求大气光估值,同时使用引导滤波细化介质透射率。最后,使用优化的大气光值和透射率对已增强图像复原。经过对比分析,新算法在主客观方面都有明显提升。
关键词:分数阶;Al-Alaoui算子;四叉树;暗通道;图像去雾
中图分类号:TP391.4 文献标识码:A 文章编号:2096-4706(2024)08-0151-05
DOI:10.19850/j.cnki.2096-4706.2024.08.033
0 引 言
在计算机视觉技术、传感器技术日新月异的时代背景下,数字图像处理广泛用于智能交通、视频监控、军事侦察、图像判读、导航定位等领域。而在雾霾天气下,空气中悬浮的大量微粒(如水气、尘埃等)会散射、吸收光线,衰减目标物体的反射光,致使光学设备采集到的图像呈现颜色衰减、对比度下降、细节模糊不清晰等现象。低质、失真的雾图对上述应用带来诸多不利影响。因此,研究快速有效的去雾算法,提高图像质量具有重要意义和应用价值。
图像去雾的研究最早可追溯到20世纪50年代,美国学者针对地球资源卫星图像云雾退化问题所展开的工作。八十多年来,伴随着计算机技术的高速发展,国内外众多学者在图像去雾上的研究取得了许多突破性的进展。根据去雾原理的不同,大致分为基于图像增强的去雾算法、基于物理模型的去雾算法和基于深度学习的去雾算法三大类[1,2]。其中,基于单幅图像增强的算法主要有直方图均衡化[3]、Retinex理论算法[4,5]、同态滤波、小波[6]和曲波变换等。该类方法不考虑图像降质的原因,只是按照特定需要突出图像中的某些信息,同时削减或去除某些不需要处理的信息。基于物理模型的去雾方法常以大气散射模型为基础,从图像退化本质进行研究,估算模型参数,逆向复原出无雾图像。最具代表性的是何凯明提出的暗通道先验去雾方法[7]。基于深度学习的去雾方法[8]则主要是利用CNN强大的学习能力,寻找有雾图像与图像复原物理模型中某些系数的映射关系,或者使用GAN,根据有雾图像还原出无雾的清晰图像。
近年来,随着分数阶微积分在图像处理中的广泛应用[9,10],学者们通过合理运用分数阶微分弱导性(在提高图像信号高频成分的同时非线性地保留信号的低频成分),将其应用到图像去雾中,也取得了显著的效果。本文基于大气散射模型,提出一种结合Al-Alaoui算子的改进暗通道先验去雾算法,从主客观评价去雾效果,都有很大提高。
1 分数阶掩膜及Al-Alaoui算子的引入
1.1 分数阶微积分的定义与掩膜构造
分数阶微积分是整数阶微积分的衍生和连续内插。主要有Grümwald-Letnikov(G-L)、Riemann-Liouville(R-L)和Caputo定义。其中G-L定义在数值实现时可以转换为卷积运算形式,适合应用在信号处理中,R-L定义常应用于计算一些较为简单函数的解析解,Caputo定义适合应用于工程领域[11]。
分数阶微积分G-L定义是通过将整数阶微积分的差分近似以递推形式求极限推衍而来。表达式为:
(1)
式(1)中,D表示分数阶微分,GL表示G-L定义,分数阶次用α表示,Γ(α)为Gamma函数。
对取值范围x ∈ [a,b]的函数进行离散化表示,将取值区间单位间隔等分h = 1,n = [x-a],可推导出数字滤波器的差分形式:
(2)
根据式(2)写出对应的差分系数:
(3)
假设二维图像信号对于X轴和Y轴方向的分数阶微积分在一定条件下是可分离的,为实现抗旋转性和缩放不变性,设计构造出如图1所示的分数阶微积分掩膜算子。考虑到离中心像素越远的点与其相关性越小,若n取值过大,计算将变得复杂,增加计算时间,故n的值一般不大于3。
1.2 Al-Alaoui算子
Al-Alaoui算子是根据矩形算子1-z-1和梯形算子2 (1-z-1) / (1+z-1)在高频处频域特征互补特性而提出[12],将这2种算子按照3:1比例结合,表达式为:
(4)
对比矩形算子和梯形算子,Al-Alaoui算子在高频处具有更好的频域特性,代入z = ejω,Al-Alaoui算子的分数阶滤波函数为:
(5)
为实现基于Al-Alaoui算子的分数阶FIR数字微积分滤波器的设计,将" 因式分解,再利用因式与一阶鲁比希加权系数" 生成函数的关系可展开为:
(6)
式(6)中, 表示1阶逼近的鲁比希加权系数,等价于 ,G-L加权系数,
(7)
通过时域卷积频域相乘的性质,利用矩形窗函数将上述滤波器传递函数截断为有限项,得 [13]。
(8)
式(8)中" 表示Al-Alaoui算子的分数阶FIR数字微积分滤波器" 截断后的系数,取截断系数的前三项,代入图1中的掩膜,构造5×5的Al-Alaoui算子掩膜如图2所示,取分数阶次α = 0.5,与雾图做卷积滤波处理,增强图像的纹理细节,平滑图像低频部分。
2 暗通道先验理论
基于图像增强的去雾方法因未考虑图像退化降质原因,而是直接最大限度地从每个通道提取信息,来提高图像信息的利用率,这样容易造成颜色、纹理等信息的损失,引起图像失真,去雾效果一般。相比之下,基于物理模型的去雾算法具有更稳定高效的性能。该类算法将大气散射模型描述为:
(9)
式(9)中,I (x,y)表示设备采集到的含雾图像,J (x,y)表示对应场景的无雾图像,A表示大气光照强度,t (x,y)表示介质透射率,假设大气光均匀同质,t (x,y)=e-λd (x,y),λ表示大气散射系数,d (x,y)表示场景深度。
式(9)右边第一项为直接衰减项,描述了场景目标反射光在介质中的衰减;第二项为大气光幕,反映了全局大气光的散射导致图像景物颜色的偏移。该模型是一个欠约束病态求解问题,研究者们相继提出了对应策略。其中,最具影响力的是何凯明(He)等提出的暗通道先验(Dark Channel Prior,DCP)去雾算法。
He等通过对大量无雾图像统计分析发现,无雾图像中绝大部分非天空区域总能找到亮度值很低或亮度值接近于零的像素点。即无雾图像中的暗通道可以表示为:
(10)
式(10)中,J c表示J的一个确定的RGB颜色通道,Jdark (x,y)表示暗通道图像。Ω表示以像素点x为中心的方形局部区域。
He等挑选暗通道最亮的0.1%像素作为雾最浓的像素点,并将原图I中对应像素中亮度最大的像素均值作为大气光的估计值A。
由大气光在局部区域内均匀同质的假设可知,t (x,y)在Ω (x,y)内为常数,对式(9)变形并对等式两边求最小值,再代入式(10)可得:
(11)
此时,已知大气光照强度值A和介质透射率t (x,y),由式(9)可求得去雾图像J (x,y)。
(12)
t0表示一个透射率的下限阈值,为了避免去雾图像J (x,y)的值偏大导致图像过曝。取t0 = 0.1。
此后,He等用软抠图方法(soft matting)对透射率分布进行优化,又引入引导滤波对原始图像进行保边平滑。然而,此方法不适用于有大面积天空区域或白色场景的图像,且去雾后容易产生光晕效应或严重的色彩失真。
3 本文算法
对于以大气散射模型为基础的去雾算法,其核心是合理地预估出待去雾图像大气光以及透射率的值,实现有雾图像的去雾化。本文在DPC算法的基础上,对大气光值和透射率进行优化。
3.1 大气光估计
先将经Al-Alaoui算子预处理的图像二次滤波,求得暗通道图。然后根据四叉树[14]分解方法,将暗通道图平均分成四大块,分别计算每块均值减去标准差的得分,再将得分最高的块做迭代处理,继续分块并计算得分,重复该操作直到选取的区域小于预定义的范围时终止。在最终区域对应的像素中,选取一个与(255,255,255)最小距离的像素,将该像素坐标对应的暗通道值作为大气光估计值。
3.2 介质透射率优化
引导滤波的假设前提是引导滤波与输出图像之间存在局部线性关系:
(13)
式(13)中,Ji表示滤波输出图像,Ii表示引导图像,ωk表示以像素k为中心的方形窗口,ak和bk表示两个在窗口ωk下的线性系数,可通过线性回归求解代价函数得到。
考虑到每个窗口对应的ak和bk不同,因此对所有所有包含像素点i的窗口ωk邻域的输出结果计算均值,得到优化的引导滤波的计算式为:
(14)
3.3 算法流程图
本文算法流程图如图3所示。
4 实验结果与分析
本文实验均在MATLAB平台上进行,MATLAB版本为R2022b,PC处理器为2.50 GHz Intel(R)Core(TM)i5-12500H,操作系统为Windows 11家庭中文版。
4.1 实验结果图
文章选取了4种场景的含雾图像,其中1)天空区域较大;2)雾浓,包含事物特征多,纹理丰富;
3)含雾浓度较低,色调单一偏红;4)多为远景,偏暗。分别使用传统DPC算法[15]、多尺度Retinex算法(Msrcr算法)[16]、Kim算法[17,18]和本文算法对图像做去雾处理,实验效果如图4所示。
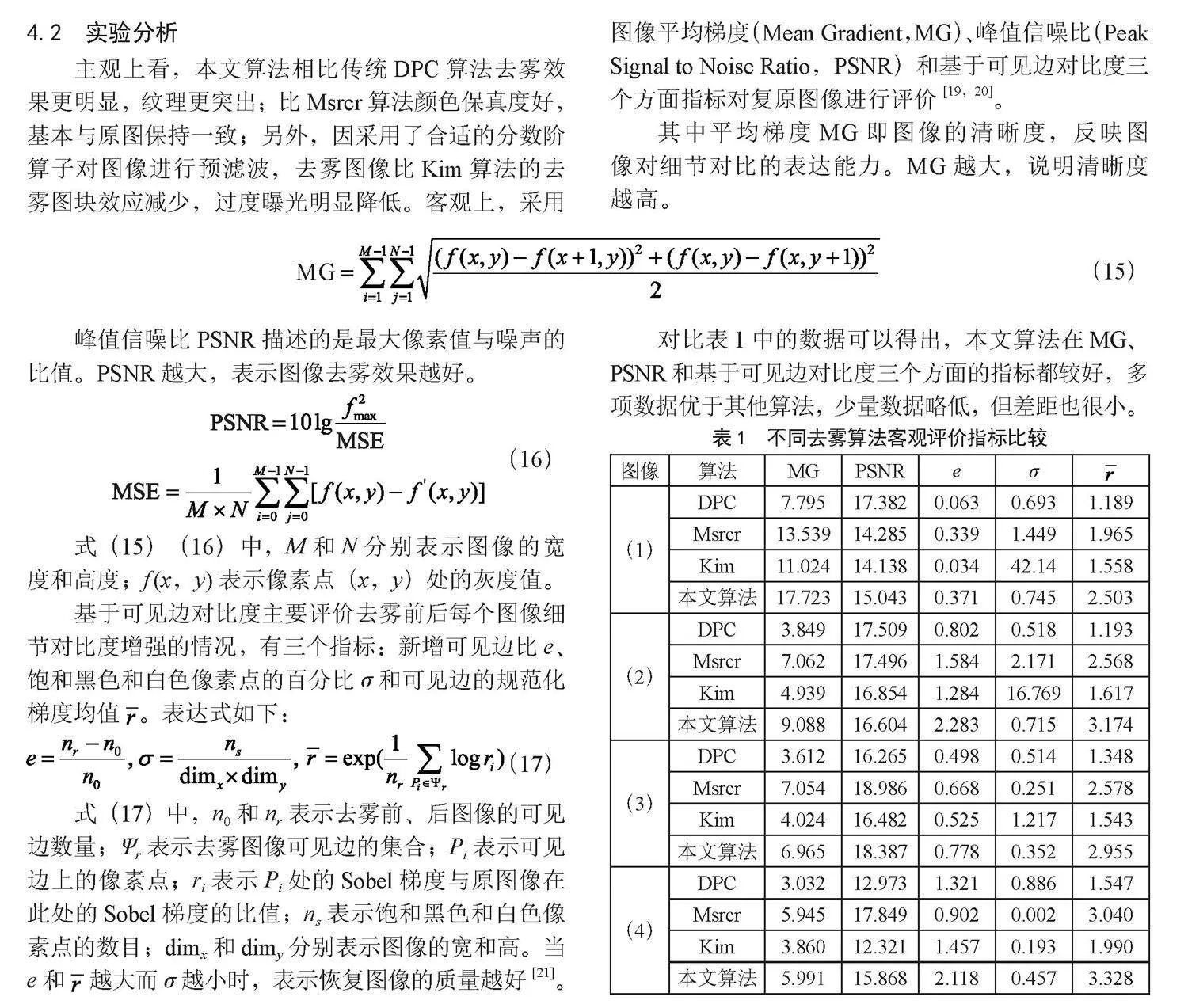
4.2 实验分析
主观上看,本文算法相比传统DPC算法去雾效果更明显,纹理更突出;比Msrcr算法颜色保真度好,基本与原图保持一致;另外,因采用了合适的分数阶算子对图像进行预滤波,去雾图像比Kim算法的去雾图块效应减少,过度曝光明显降低。客观上,采用图像平均梯度(Mean Gradient,MG)、峰值信噪比(Peak Signal to Noise Ratio,PSNR)和基于可见边对比度三个方面指标对复原图像进行评价[19,20]。
其中平均梯度MG即图像的清晰度,反映图像对细节对比的表达能力。MG越大,说明清晰度越高。
峰值信噪比PSNR描述的是最大像素值与噪声的比值。PSNR越大,表示图像去雾效果越好。
(16)
式(15)(16)中,M和N分别表示图像的宽度和高度;f (x,y)表示像素点(x,y)处的灰度值。
基于可见边对比度主要评价去雾前后每个图像细节对比度增强的情况,有三个指标:新增可见边比e、饱和黑色和白色像素点的百分比σ和可见边的规范化梯度均值 。表达式如下:
(17)
式(17)中,n0和nr表示去雾前、后图像的可见边数量;Ψr表示去雾图像可见边的集合;Pi表示可见边上的像素点;ri表示Pi处的Sobel梯度与原图像在此处的Sobel梯度的比值;ns表示饱和黑色和白色像素点的数目;dimx和dimy分别表示图像的宽和高。当e和" 越大而σ越小时,表示恢复图像的质量越好[21]。
对比表1中的数据可以得出,本文算法在MG、PSNR和基于可见边对比度三个方面的指标都较好,多项数据优于其他算法,少量数据略低,但差距也很小。
总的来说,本文算法在主客观上都能达到令人满意的去雾效果,能有效弥补经典去雾算法存在的不足,且适用于多种场景,不同浓度的雾图复原。
5 结 论
文章从传统图像去雾方法存在的不足出发,思考改进提高的算法。先用分数阶Al-Alaoui算子对图像做卷积滤波增强处理,再使用优化的大气光值和透射率对图像去雾处理。经过与多种经典算法对比,实验结果和测试数据证实了本文算法的有效性和可行性。下步还可以探索使用不同阶次、不同分数阶算子,在不同时机、不同域对图像做去雾研究,争取理论和实践的双突破。
参考文献:
[1] 张登银,鞠铭烨,钱雯.图像去雾算法研究现状与展望 [J].南京邮电大学学报:自然科学版,2020,40(5):101-111.
[2] 谢勇,贾惠珍,王同罕,等.图像去雾算法综述 [J].计算机与数字工程,2022,50(12):2765-2774.
[3] 吴成茂.直方图均衡化的数学模型研究 [J].电子学报,2013,41(3):598-602.
[4] 林东升.三种Retinex图像去雾算法比较与分析 [J].电脑知识与技术,2020,16(32):197-198.
[5] 汪林林,余梅,安超.模糊多尺度Retinex彩色图像增强 [J].计算机工程与应用,2012,48(7):174-176.
[6] 董静薇,赵春丽,海博.融合同态滤波和小波变换的图像去雾算法研究 [J].哈尔滨理工大学学报,2019,24(1):66-70.
[7] HE K,SUN J,TANG X.Single Image Haze Removal Using Dark Channel Prior [J].IEEE transactions on pattern analysis and machine intelligence,2011,33(12):2341-2353.
[8] 钱雯.基于深度学习的图像去雾算法研究 [D].南京:南京邮电大学,2020.
[9] 蒲亦非,王卫星.数字图像的分数阶微分掩模及其数值运算规则 [J].自动化学报,2007(11):1128-1135.
[10] 黄果,许黎,蒲亦非.分数阶微积分在图像处理中的研究综述 [J].计算机应用研究,2012,29(2):414-420+426.
[11] PODLUBNY I.分数微积分:理论基础与应用导论 [M].袁晓,译.北京:电子工业出版社,2021:106-113.
[12] 宋保业,许琳,卢晓,等. 基于变参数Al-Alaoui变换的分数阶微积分算子离散化 [C]//第三十四届中国控制会议论文集(D卷).杭州:[出版者不详],2015:1475-1479.
[13] 李琪,周宇,和浩铭,等.分数阶数字FIR微分器的快速WSLD设计算法 [J].太赫兹科学与电子信息学报,2023,21(5):652-660+670.
[14] 田健.基于四叉树和块区域的单幅图像去雾算法研究 [D].开封:河南大学,2018.
[15] CAI B L,XU X M,JIA K,et al. Dehazenet:anend-to-end system for single image haze removal [J].IEEE Transactions on Image Processing,2016,25(11):5187-5198.
[16] 曾铭萱,李娟,许志猛,等.结合多尺度和分数阶微分的单幅图像去雾算法 [J].福州大学学报:自然科学版,2022,50(3):330-336.
[17] KIM J,JANG W,SIM J,et al. Optimized contrast enhancement for real-time image and video dehazing [J].Journal of Visual Communication and Image Representation,2013,24(3):410-425.
[18] KIM J H,SIM J Y,KIM C S.Single image dehazing based on contrast enhancement [C]//IEEE International Conference on Acoustics,Speech and Signal Processing (ICASSP).Prague:IEEE,2011:1273-1276.
[19] 韩昊男,钱锋,吕建威,等.改进暗通道先验的航空图像去雾 [J].光学精密工程,2020,28(6):1387-1394.
[20] 韩昊男,钱锋,吕建威,等.图像去雾方法质量评价 [J].光学精密工程,2022,30(6):721-733.
[21] 王成文.基于物理模型的单幅图像去雾方法 [M].北京:科学出版社,2019:41-44.
作者简介:张伟(1990—),男,汉族,四川岳池人,硕士研究生,主要研究方向:分数微积分应用、图像去雾处理;李琪(1997—),女,汉族,四川简阳人,硕士在读,主要研究方向:信号与信息处理;袁晓(1964—),男,汉族,四川中江人,副教授,博士,主要研究方向:现代信息信号处理、分数微积分理论与应用、现代电路与系统理论与技术。
收稿日期:2023-09-14
A Image Dehazing Algorithm Combined with Al-Alaoui Operator and Improved
Dark Channel
ZHANG Wei, LI Qi, YUAN Xiao
(College of Electronics and Information Engineering, Sichuan University, Chengdu 610064, China)
Abstract: Aiming at the problems of limited effect, halo effect and color distortion in traditional image dehazing methods, a priori dehazing algorithm combined with Al-Alaoui operator and improved dark channel is proposed in this paper. Firstly, Al-Alaoui operator is used to enhance the image by convolution filtering, then the improved quadtree search method is used to estimate the atmospheric light, and the guided filter is used to refine the medium transmittance. Finally, the enhanced image is restored using the optimized atmospheric light value and transmittance. After comparative analysis, the new algorithm has obvious improvement in both subjective and objective aspects.
Keywords: fractional order; Al-Alaoui operator; quadtree; dark channel; image dehazing