





摘 要:针对目前云服务市场中如何快速有效为客户提供最优组合云服务问题,提出一种包括灰色关联和自适应遗传算法的两阶段云服务组合优化算法。首先根据用户云服务需求,利用灰色关联分析对云服务进行初步筛选形成候选云服务集;其次建立时间最短、成本最低、可用性、互操作性、可扩展性和满意度最佳的多目标决策模型,采用自适应遗传算法求解模型,确定最优云服务组合方案;最后通过算例证明该算法在解决最佳云服务组合方面的合理性和科学性。
关键词:云服务组合;灰色关联分析;改进遗传算法;多目标决策
中图分类号:TP391 文献标识码:A 文章编号:2096-4706(2024)08-0115-08
DOI:10.19850/j.cnki.2096-4706.2024.08.026
0 引 言
近十年来,云计算凭借部署简单、可靠性高、伸缩性好等优点逐渐被企业所接受。国内云计算已经从概念导入进入广泛普及、应用繁荣的新阶段,云计算成为数字经济背景下企业数字化转型的必然选择,企业上云进程进一步加速。随着云计算服务功能丰富和市场扩大,云计算应用的不断深入,用户对云服务的需求也愈发复杂,传统的单一云服务类型无法满足用户复杂的业务需求。因此通过云服务的组合来满足用户复杂业务需求显得至关重要。
针对云服务组合问题,很多学者构造云服务组合优化的决策模型,将云服务组合问题作为满足多个服务质量(quality of services, QoS)目标要求的多目标决策问题[1]。付超等提出了云制造环境下的云服务组合多目标规划模型[2]。Mostafa等采用两种多目标方法来解决具有冲突目的和对质量矩阵不同限制的服务组合问题[3]。Dahan认为随着云服务种类丰富,基于服务质量QoS的云服务组合具有NP-Hard问题特征[4]。启发式机制算法常被应用于求解云服务组合优化问题。Karimi等根据云服务中的SLA合同确定的组合要求,采用关联规则和遗传算法等来减少组合时间、提高算法性能[5]。Zhou等针对不同云服务组合多目标优化问题,分析如何选择合适的多目标进化算法[6]。Potluri等根据云服务QoS采用两阶段云服务推荐模型对云服务进行排序[7]。还有学者采用入侵性杂草优化算法(IWO)[8]、多智能体蚁群算法[6]、自适应遗传算法[9]、改进北极熊算法[10]等智能优化算法求解云服务组合问题。以上研究主要从时间、成本、性能、资源调度等角度研究云服务组合问题,较少综合考虑用户对云服务使用评价因素。另外在组合优化算法求解上,较少有考虑云服务数量多、组合优化效率低下等问题。考虑以上问题,本文在已有研究成果上,构建云服务组合QoS测度模型并提出一种包括灰色关联和改进遗传算法的两阶段云服务组合优化算法。
1 云服务组合问题和模型
1.1 云服务组合问题和模型
云服务组合是指云服务平台选择并组合云服务资源完成用户云服务需求的过程[1]。云服务组合优化的流程如图1所示。
具体步骤如下:
1)用户向云服务平台提交云服务需求。
2)将用户需求按照不同类型分解成若干云服务子任务,并针对每项子任务匹配满足要求的云服务资源集。
3)判定用户的云服务模式,如果为单一模式进入步骤四,否则进入步骤五。
4)在满足用户需求的云服务资源池中,选择最优的云服务推荐给用户。
5)对于用户复杂多样的云服务需求,则选择组合服务模式。云平台根据用户QoS目标,筛选出各子任务的候选云服务集。
6)通过云服务组合优化,得到最优的云服务组合,完成用户云服务任务。
为了实现云服务组合优化,选取科学、合理和可行的云服务评价指标尤为关键。目前学者们大多是基于成本、执行时间、可靠性、可用性、安全性等常用指标[11-13]来构建云服务质量QoS指标体系。本文在现有服务QoS评价指标基础上,结合用户对云服务的满意度,建立云服务组合优化的QoS评价指标体系,主要包括:时间、成本、可用性、互操作性、可扩展性、满意度。借鉴Web服务、云计算服务的相关QoS测度方法,可以定义云服务QoS属性的计算方法。
1)时间(Time, T)是指从用户提交云服务请求到获得服务执行结果所需的时间[1]。时间的测度主要包括服务响应时间和服务执行时间。
2)成本(Cost, C)是指用户在单位时间内使用某类云服务所需支付的费用[5]。
3)可用性(Availability)。可用性(A)指云服务能在特定时间、特定条件下被用户成功访问的能力,该指标综合了系统可用性、可靠性和可服务性的概念[14]。
4)互操作性(Interoperability, In)是云服务与提供商的其他平台服务或其他服务提供商的云服务之间的交互能力。互操作性也是用户选择云服务要考虑的一个重要因素,可以定义为:In = Np / Nc,其中Np为提供商支持的平台数,Nc为客户要求支持的平台数[15]。
5)可扩展性(Scalability, Sc)是指用户可以根据实际业务需求的增加自动或手动地扩展其云服务资源;同样,当业务需求减少时,亦可根据用户需求释放云服务资源[14]。
6)满意度(Satisfaction, Sa)是表示用户对云服务的期望值与用户实际体验之间的匹配程度。满意度的测量值直接利用云服务平台上用户对云服务的评价数据。
1.2 云服务组合问题建模
云服务组合优化的最终目标是根据用户云服务需求,从候选的云服务资源中选取最优云服务组合使得完成云服务任务的时间最短、成本最低、可用性、互操作性和可扩展性最好、满意度最佳。
该问题的数学描述如下:假设用户的云服务需求为S = {si i = 1,2,…,n},表示云服务需求是由n项云服务任务组成的集合;对于云服务任务si存在候选云服务集CSi = {csij i = 1,2,…,n,j = 1,2,…,mi},其中mi为si对应的候选云服务数量;云服务任务si的对应QoS属性集合为:QCSij = {TCSij,CCSij,ACSij,InCSij,ScCSij,SaCSij},其中TCSij为时间、CCSij为成本、ACSij为可用性、InCSij为互操作性、ScCSij为可扩展性、SaCSij为满意度。T ( fi )、C ( fi )、A ( fi )、In ( fi )、Sc ( fi )、
Sa ( fi )分别为完成云服务组合任务所需要的总时间、总成本、总可用性、总互操作性、总扩展性和总满意度。云服务组合优化的目标可采用如下目标函数表示:
(1)
针对该多目标优化决策问题,可以利用线性加权法将其转化为单目标优化决策问题,为此可以采用如下目标函数表示:
(2)
其中,w1、w2、w3、w4、w5、w6分别为QoS属性时间、成本、可用性、互操作性、扩展性和满意度的权重系数,且满足 。
2 云服务组合优化模型求解
2.1 云服务组合优化QoS指标测度方法
任何一个云服务组合路径都可以由顺序结构、并行结构、选择结构和循环结构四种基本结构组成,如图2所示。
基于四种结构的QoS值,可得云服务组合的QoS目标值:QCS={T ( fi ),C ( fi ),A ( fi ),In ( fi ),Sc ( fi ),
Sa ( fi )}。其中T ( fi )、C ( fi )、A ( fi )、In ( fi )、Sc ( fi )、Sa ( fi )的计算采用文献[2]中四类基本结构下的云服务组合QoS的计算方法,如表1所示。
表中,λi为选择结构中云服务csij被选中的概率,满足 ;θ为云服务循环的次数; 为0—1变量,表示云服务任务i由csij服务完成。
2.2 基于灰色关联分析的云服务集筛选
云服务平台中云服务种类繁多、数量巨大,不同云服务商的云服务之间水平差异也较大。直接进行云服务组合优化求解可能存在云服务组合数量较为庞大且计算效率低等问题。云服务的初始筛选对随后的云服务组合优化有重要作用,通过筛选QoS属性指标值较差的云服务,能缩小云服务组合优化问题的解空间,进而提高云服务组合的效率。本文拟运用灰色关联分析法进行云服务筛选[16],具体过程如下:
1)构建决策矩阵。设云服务类型Si(i = 1,2,…,n)中存在mk个候选云服务、n个属性,xij为云服务类型Si中第i个候选云服务的j指标值。则云服务类型Si的初始决策矩阵M为M = (xij)mk×n。采用线性标度转换法对决策矩阵作规范化处理,用式(3)对获益性和损失性目标属性的规范化分别进行计算,得规范化决策矩阵V = (vij)mk×n。
(3)
2)确定理想方案与负理想方案。根据决策矩阵V,可得理想方案A*和负理想方案A-,即:
(4)
(5)
其中,J1和J2分别为获益性、损失性指标,式(4)表示理想方案A*由各目标属性下最好的属性值组成,式(5)表示负理想方案A-由各个目标属性最差的属性值组成。
3)计算候选云服务方案与理想云服务方案和负理想云服务方案间的灰色关联度。首先分别利用式(6)、式(7)计算第i个候选云服务与理想方案和负理想方案关于第j个指标的灰色关联系数 、:
(6)
(7)
其中,ρ为分辨系数,ρ ∈ [0,1],通常取值ρ = 0.5。则第i个候选云服务与理想方案和负理想方案的灰色关联度分别为:
(8)
(9)
4)计算候选云服务方案的灰色关联相对贴近度:
(10)
根据相对贴近度的Ci的大小顺序,排列各云服务类型中候选云服务,从而筛选排序靠前的云服务作为各云服务类型的备选云服务。
2.3 基于自适应遗传算法的云服务组合优化
云服务组合优化问题是典型的多目标优化问题,文本采用自适应遗传算法(AGA)来求解云服务组合优化问题[17],具体步骤如下:
1)染色体编码方式。根据遗传算法二进制编码特征,每一个染色体即云服务组合可以用如图3所示的二进制代码串来表示,代码串中uij代表一个候选云服务的状态,当uij = 1表示任务Si的第j个候选云服务被选中,uij = 0表示未被选中。因此云服务组合优化问题就转换成求解最优染色体编码问题。
2)适应度函数。遗传算法中种群内个体遗传到下一代的机会取决于个体适应度值,因此所有个体的适应度fitness (x)必须为非负数。将(2)式目标函数进行转换,可以取:
fitness (x) = Z (x) + c (11)
其中Z (x)为目标函数,c为非负整数,使得满足fitness (x)>0即可。
3)选择操作。选择操作主要依据“优胜劣汰”原则,为了保证最佳的云服务资源能进入下一代新群体中,本文采用轮盘赌法,设种群数为M,个体i的适应度为fiti,整个种群适应度为 ,则个体i的选择概率Pi可以用公式表为:
(12)
若个体的选择概率大,则能被多次选择,其遗传基因会进一步在种群中扩大;若个体的选择概率小,则被淘汰。这样通过选择操作保证了种群进化过程中优良个体数目越来越多。
4)自适应交叉和变异概率。在标准遗传算法中,交叉概率Pc和变异概率Pm一般为固定值,这样很容易造成遗传算法的早熟,Pc和Pm越大,新个体更新速度加快,但后代的遗传特征变化更大,使得高适应度的个体可能会丢失。而当Pc和Pm越小时,个体适应度较为平稳,个体更新的速度就越慢。而AGA采用自适应的交叉概率Pc和变异概率Pm,让每个个体的交叉概率Pc和变异概率Pm随个体的适应度变化而变化。对适应度较小的个体,适当增大其Pc和Pm,以加速个体更新速度;对适应度较大的个体,Pc和Pm相应减少,使较优解不易丢失。这样种群中的每个个体对外界环境的变化就具有自适应能力。
设在遗传过程中,较差个体和较优个体的交叉概率分别为Pc0和Pc1(Pc0>Pc1);较差个体和较优个体的变异概率分别为Pm0和Pm1(Pm0>Pm1),并设定以上概率的取值范围:Pc0,Pc1 ∈ [0.2,0.7],Pm0,Pm1 ∈ [0.1,0.5]。种群中的最大适应度和平均适应度分别为fitmax和fitavg,执行交叉操作两个体适应度的较小值为fitsmall,执行变异操作个体的适应度为fitmut。则自适应遗传算法的交叉概率Pc可以用下式表示:
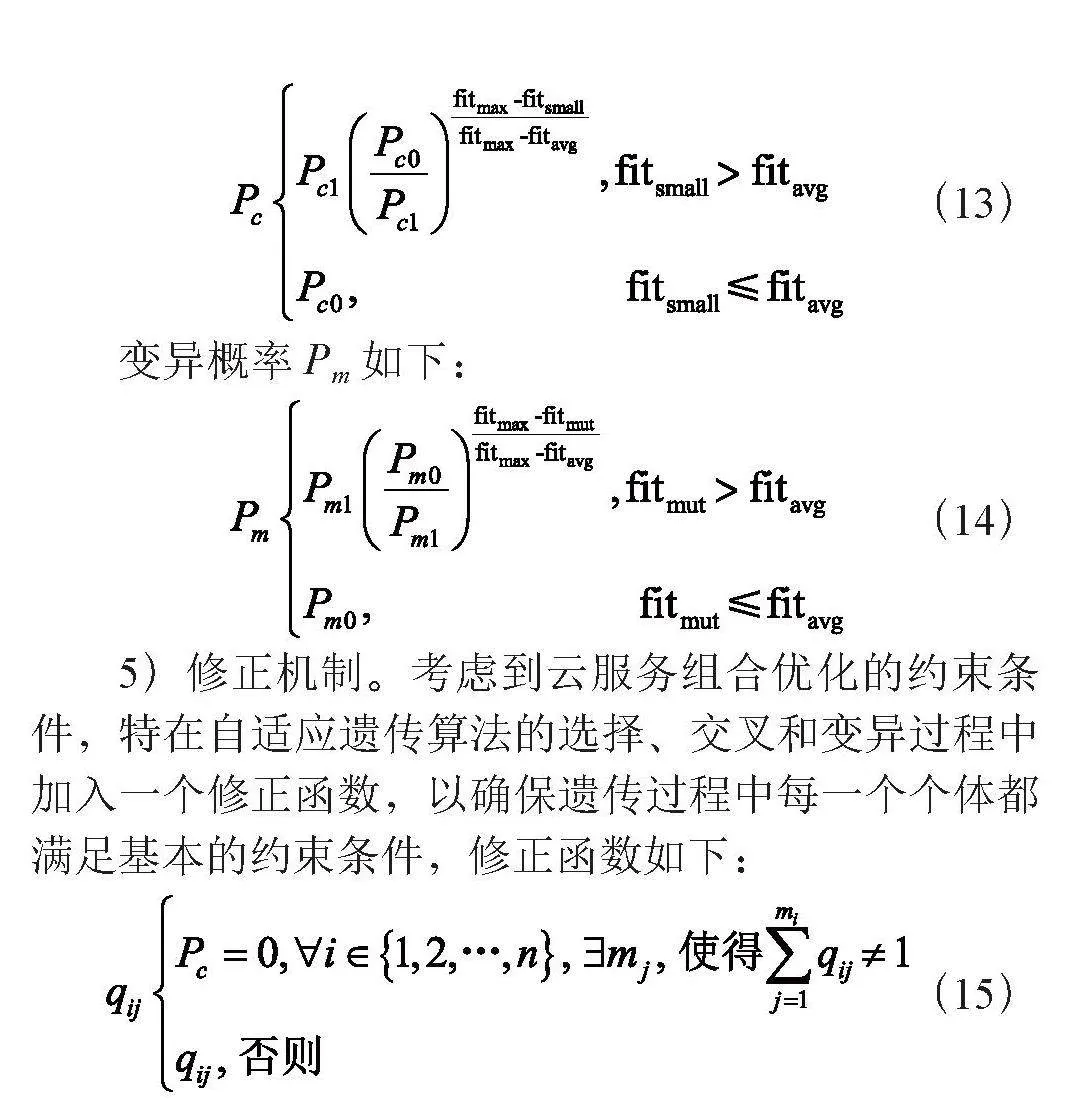
(13)
变异概率Pm如下:
(14)
5)修正机制。考虑到云服务组合优化的约束条件,特在自适应遗传算法的选择、交叉和变异过程中加入一个修正函数,以确保遗传过程中每一个个体都满足基本的约束条件,修正函数如下:
(15)
其中,qij为遗传过程中产生的一个个体,如果该个体不满足约束条件,则将该个体直接从种群中淘汰,重新进行种群的选择、交叉和变异操作,直到生成的个体满足基本约束条件,才作为有效的新个体。
6)自适应遗传算法步骤。根据上述建立的自适应遗传算法求解方法,利用MATLAB遗传算法工具箱GATBX对该模型进行求解[18]。具体步骤如下:
步骤一:参数定义。首先设定自适应遗传算法相关参数,包括种群初始个体数目,最大遗传代数、选择概率、较差个体和较优个体的交叉概率、较差个体和较优个体的变异概率。
步骤二:初始种群的产生。按照给定的种群个体数目和基因位长度,利用crtbp函数进行种群初始化,令迭代代数gen=1。
步骤三:如果gen已经达到最大迭代代数,转到步骤九,否则转到步骤四。
步骤四:适应度值计算。按照式(11)计算种群中个体的适应度,并统计种群的最大适应度值和平均适应度值。
步骤五:选择操作。采用轮盘赌法,通过select函数进行选择操作得到子代新种群。
步骤六:交叉操作。对种群中的个体进行随机配对,若随机配对个体中有个体的适应度值为最大适应度值,则保留该个体,否则按照式(13)计算自适应交叉概率,通过recombin函数进行交叉重组操作。
步骤七:变异操作。按照式(14)计算自适应变异概率,通过mut函数进行变异操作。
步骤八:令gen=gen+1,转到步骤三。
步骤九:将具有最大适应度值的个体作为云服务组合的最优解,算法结束。
3 案例分析
3.1 服务QoS属性样本数据收集
考虑某信息通讯企业将企业的云服务需求提交给某云服务平台,按照云服务类别,平台将企业需求分解为计算服务(IaaS服务)和存储服务(IaaS服务)、客户关系管理系统(SaaS服务)和OA(SaaS服务)四类子任务,即用户的云服务任务为S = {S1,S2,S3,S4},表示用户云服务任务是4项云服务组成的集合。假定用户的各项云服务都按照顺序结构执行,则每个子任务的初始候选云服务资源如图4所示,各候选云服务的相关QoS属性值:时间T、成本C、可用性A、互操作性In、可扩展性Sc、满意度Sa,如表2所示。本文要求用户的每项云服务任务选择一个对应的云服务,云服务组合优化的目标是找出满足用户需求的最佳云服务组合。
注:表中成本、满意度数据来自aliyun.com市场,时间、可用性、互操作性和可扩展性的数据为模拟数据,实际应用中核心云平台可以根据需要进行测试收集这四项数据。
3.2 基于灰色关联分析的初始云服务集筛选
1)针对表2中指标量纲不一致问题,采用线性标度法对每种云服务类型分别进行规范化处理,即利用式(3)对时间、成本两个损失性指标和可用性、互操作性、可扩展性和满意度四个获益性指标分别进行计算,得到规范化QoS属性值。
2)利用式(4)、式(5)可以求得计算服务(IaaS服务)和存储服务(IaaS)、CRM(SaaS服务)和OA(SaaS服务)四类云服务子任务中的理想方案和负理想方案分别为:
; (16)
3)根据式(16),分别利用式(6)、式(7)计算候选云服务与理想方案和负理想方案QoS指标之间的灰色关联系数;再利用式(8)~(10)计算候选云服务与理想方案和负理想方案的灰色关联度、与理想方案的相对贴近度,结果如表3所示。并对四类云服务任务进行排序,剔除掉每类云服务中排序靠后的云服务,筛选出较优的候选云服务,如图5所示。
3.3 基于自适应遗传算法的云服务组合优化
针对筛选出的云服务集,利用自适应遗传算法求解最优的云服务组合。
1)对筛选后的云服务集进行规范化。对筛选后的候选云服务集按照云服务类型分别进行规范化处理,利用向量规范化法,即 ,对时间、成本、互操作性、可扩展性和满意度五个QoS属性指标进行计算,针对可用性QoS组合计算中累积的特征,利用" 对其进行规范化,得到规范化QoS数据,如表4所示。
2)QoS属性权重确定。按照Satty标度法对企业和相关专家进行问卷调查,对云服务的QoS属性指标进行重要度评价,按照企业的需求,确定云服务的六个QoS属性指标的权重系数w分别是w1 = 0.075,w2 = 0.216,w3 = 0.28,w4 = 0.04,w5 = 0.075,w6 = 0.315。
3)自适应遗传算法求解过程。针对候选云服务集(图5),使用QoS属性规范化数据(表4)和对应的指标权重系数值,利用自适应遗传算法求解最优的云服务组合使得式(2)的目标函数达到最小值,其中云服务组合的总时间、总成本、总可用性、总互操作性、总扩展性和总满意度分别根据QoS组合公式中的顺序结构对应公式进行计算。实验参数设置如表5所示。
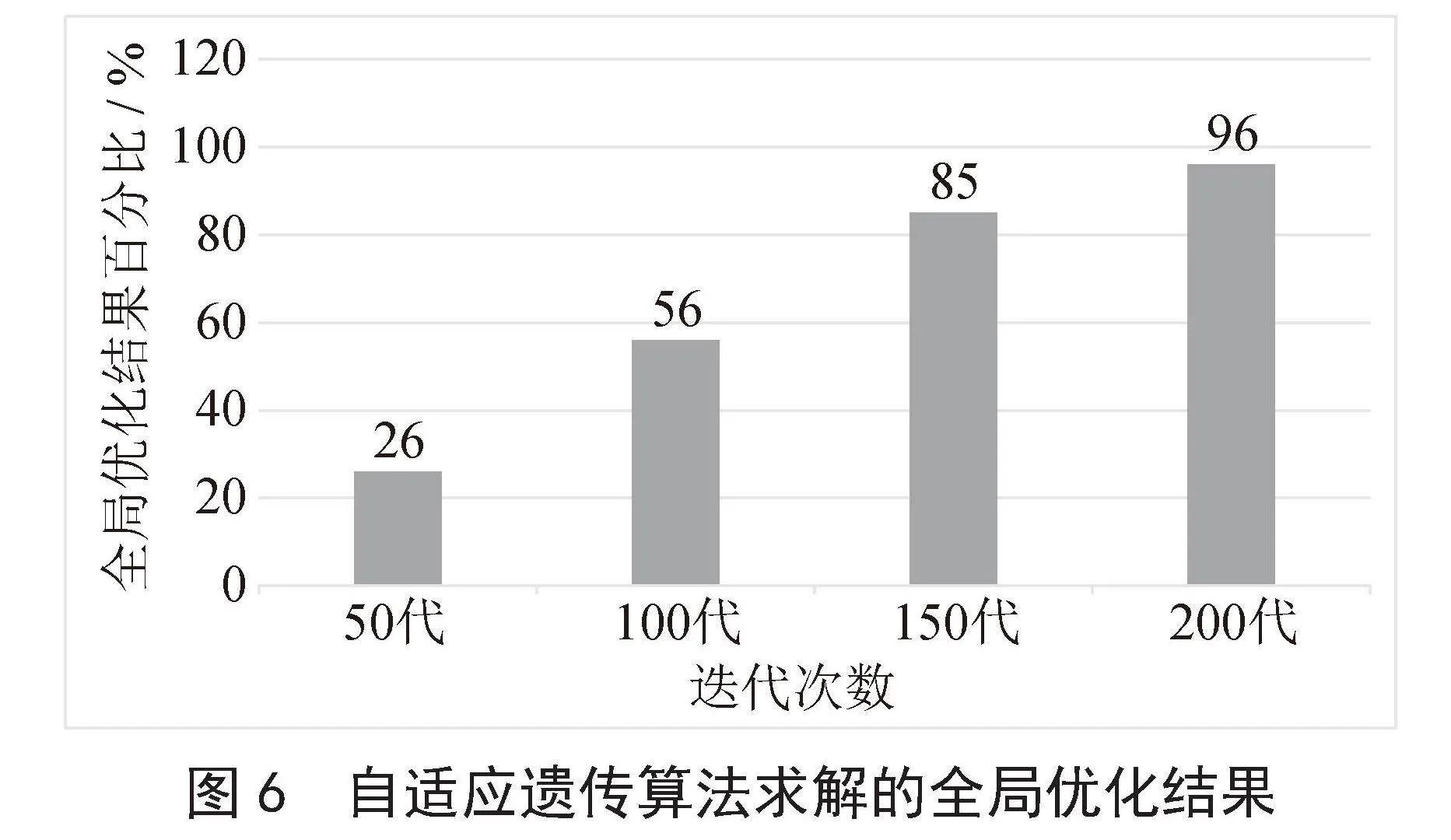
1)算法有效性验证。根据参考文献[19]的方法,选取全局优化百分数,即算法求得问题最优结果的次数占总试验次数的百分比作为验证自适应遗传算法有效性的评价指标。先利用穷举法得到云服务组合的最优解,然后利用自适应遗传算法AGA对问题进行求解,统计不同迭代次数下得到的最优解次数,进而得到全局优化结果百分数。如图6所示,迭代代数分别为50、100、150、200,试验次数为50时,所得的最优结果的次数。
由图可知,当迭代代数低于100时,得到最优解的百分比低于50%;当迭代代数大于150时,获得最优解的比例较高。因此证实自适应遗传算法对云服务组合优化问题求解的有效性。
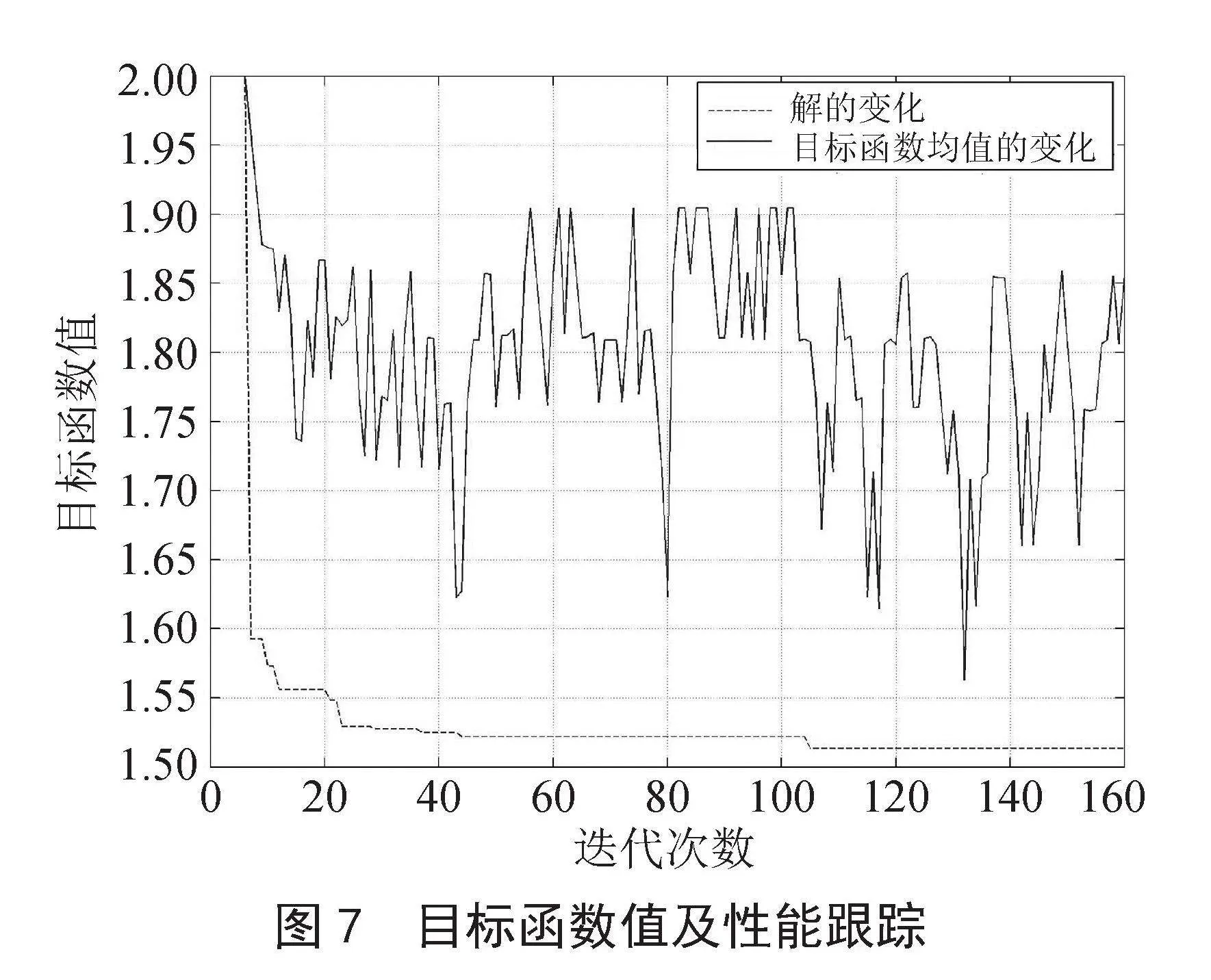
2)算法结果分析。设置迭代代数为160,通过MATLAB执行自适应遗传算法5次,选取最优结果,其目标函数均值及性能,如图7所示。
经过160代遗传后,得到最优的云服务组合的个体,最优目标函数值为1.513 4,表示满足该企业云服务任务的最优云服务组合为:{C11,C22,C31,C41}。该云服务组合完成用户云服务任务的总时间为27分钟,总成本为1 578元/年,总的可用性为92.64%,总互操作性为0.853,总可扩展性为0.733,总满意度为4.783。
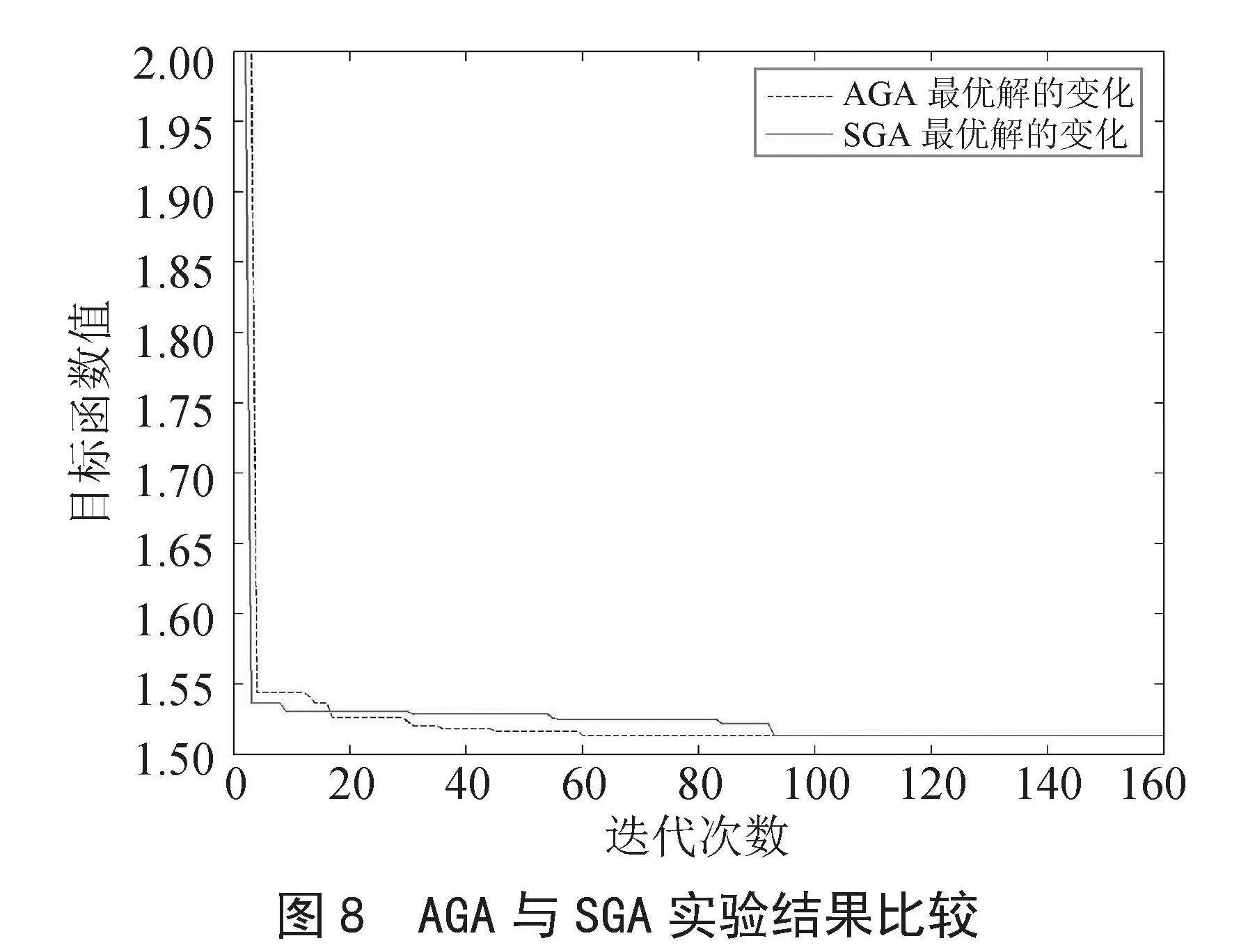
3)算法对比分析。利用MATLAB软件,设置迭代次数为160,分别利用标准遗传算法(SGA)和自适应遗传算法(AGA)各进行50次实验,结果显示采用SGA得到39次最优解,而AGA得到44次最优解,选取其中一次实验结果,如图8所示。
其中采用自适应遗传算法AGA时,当迭代达到61代时目标函数值就能达到最优解;而采用普通遗传算法SGA需要93代才能达到最优解。实验表明采用自适应遗传算法相比传统遗传算法,具有一定优越性,当用户任务数量和候选云服务数量增加时,自适应遗传算法的优越性将更加明显。
4 结 论
选择最优的云服务资源组合是完成用户复杂云服务需求的关键,云服务资源组合是否得到最优配置,具有重要的现实作用。为此本文提出一种云服务组合优化方法。首先建立包括时间、成本、可用性、互操作性、可扩展性和满意度的多QoS目标决策模型;再根据用户云服务需求,利用灰色关联分析对云服务进行筛选形成候选云服务集;采用自适应遗传算法求解多目标决策模型,确定最优云服务组合方案。最后以某企业云服务任务为例,采用上述两阶段云服务组合优化方法求解最优云服务组合,实验案例结果表明该方法的有效性和合理性。
参考文献:
[1] SHE Q P,WEI X C,NIE G H,et al. QoS-Aware Cloud Service Composition: A Systematic Mapping Study from the Perspective of Computational Intelligence [J].Expert Systems with Applications,2019,138:112804(2019-12-30).https://www.sciencedirect.com/science/article/abs/pii/S0957417419305007.
[2] 付超,肖明.云制造环境下的云服务组合优选方法 [J].计算机应用研究,2014,31(6):1744-1747+1751.
[3] MOSTAFA A,ZHANG M.Multi-Objective Service Composition in Uncertain Environments [J].IEEE Transactions on Services Computing,2015,29(1):19-28.
[4] DAHAN F. An Effective Multi-Agent Ant Colony Optimization Algorithm for QoS-Aware Cloud Service Composition [J].IEEE Access,2021,9:17196-17207.
[5] KARIMI M B,ISAZADEH A,RAHMANI A M.QoS-Aware Service Composition in Cloud Computing Using Data Mining Techniques and Genetic Algorithm [J].The Journal of Supercomputing,2016:1-29.
[6] ZHOU J J,GAO L,YAO X F,et al. Evolutionary Algorithms for Many-Objective Cloud Service Composition: Performance Assessments and Comparisons [J].Swarm and Evolutionary Computation,2019,51:1-17.
[7] POTLURI S,RAO K S. Improved Quality of Service-Based Cloud Service Ranking and Recommendation Model [J].Telkomnika,2020,18(3):1252-1258.
[8] JATOTH C,GANGADHARAN G R,FIORE U. Optimal Fitness Aware Cloud Service Composition Using Modified Invasive Weed Optimization [J].Swarm and evolutionary computation,2019,44:1073-1091.
[9] JATOTH C,GANGADHARAN G R,BUYYA R. Optimal Fitness Aware Cloud Service Composition using an Adaptive Genotypes Evolution based Genetic Algorithm [J].Future Generation Computer Systems,2019,94:185-198.
[10] 廖文利,魏乐,王宇.基于改进北极熊算法的制造云服务组合优化 [J].计算机应用研究,2022,39(4):1099-1104.
[11] 李珊,俞瑛,宋波.基于主客观综合权重的云服务时间序列选择算法 [J].计算机系统应用,2016,25(11):187-192.
[12] 鲁城华,鲁县华,钱升华.基于多层次属性建模的云制造服务优选方法 [J].计算机应用与软件,2022,39(1):79-88+218.
[13] YAGHOUBI M,MAROOSI A. Simulation and Modeling of an Improved Multi-Verse Optimization Algorithm for QoS-Aware Web Service Composition With Service level Agreements in the Cloud Environments [J].Simulation Modelling Practice and Theory,2020,103:1-16.
[14] 邓国华,陈冬林,姚梦迪.基于AHP-线性分配法的企业云计算投资决策 [J].统计与决策,2018,34(5):176-179.
[15] GARG S K,VERSTEEG S,BUYYA R. A Framework for Ranking of Cloud Computing Services [J].Future Generation Computer Systems,2013,29(4):1012–1023.
[16] 耿秀丽,杨珍.基于灰色关联预测与信任云混合算法的方案推荐 [J].计算机集成制造系统,2020,26(4):980-988.
[17] 马祖军.基于遗传算法的供应链联盟伙伴选择 [J].系统工程理论与实践,2003(9):81-84.
[18] 曾日波.Matlab遗传算法工具箱的应用 [J].兵工自动化,2005(6):115-116.
[19] 刘卫宁,刘波,孙棣华.面向多任务的制造云服务组合 [J].计算机集成制造系统,2013,19(1):199-209.
作者简介:邓国华(1984—),男,汉族,湖北武汉人,副教授,硕士研究生导师,主要研究方向:云服务管理、系统建模与仿真;丁海旭(2000—),男,汉族,湖北武汉人,硕士研究生,主要研究方向:管理系统工程;陈冬林(1970—),男,汉族,湖北安陆人,教授,博士研究生导师,主要研究方向:云计算和大数据、电子商务。
收稿日期:2023-08-07
基金项目:国家自然科学基金项目(72171102);湖北省教育厅哲学社会科学研究项目(19G028);江汉大学湖北省重点学科(管理科学与工程)开放性项目(ZDXK202019);江汉大学高层次人才科研启动经费(2018-12)
Two-Stage Cloud Service Composition Optimization Algorithm and
its Application Research
DENG Guohua1,2, DING Haixu1, CHEN Donglin3
(1.School of Business, Jianghan University, Wuhan 430056, China; 2.Wuhan Urban Circle Manufacturing Development Research Center, Jianghan University, Wuhan 430056, China; 3.School of Economics, Wuhan University of Technology, Wuhan 430070, China)
Abstract: Aiming at the problem of providing customers with the optimal composite cloud services quickly and effectively in the current cloud service market, this paper proposes, a two-stage cloud service composition and optimization algorithm which contains gray correlation and Adaptive Genetic Algorithm. Firstly, according to the users cloud service requirements, cloud services are screened by grey correlation analysis to form a candidate set of cloud services. Secondly, it constructs a multi-objective decision-making model of the shortest time, the minimum cost and the best availability, interoperability, scalability and satisfaction. It uses an Adaptive Genetic Algorithm to solve the model to determine the optimal cloud service composition scheme. Finally, an example is given to prove the rationality and scientificity of the algorithm in solving the optimal cloud service composition.
Keywords: cloud service composition; grey relation analysis; improved Genetic Algorithm; multi-objective decision-making