
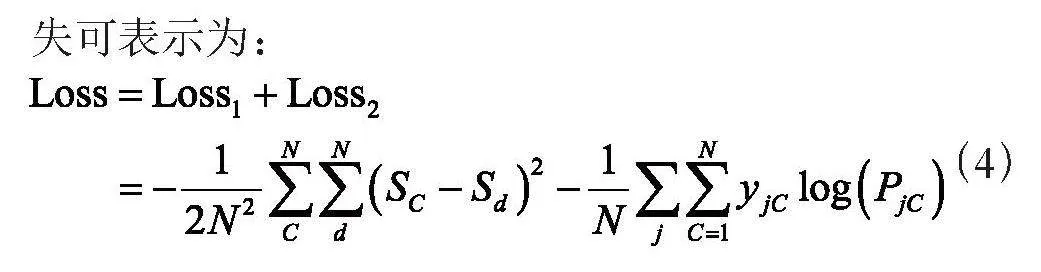
摘 要:在基于图神经网络的脑功能性疾病研究中,构建脑网络之后不再变化,且一般需要大量的数据进行建模训练。为了解决这两个问题,文章提出一种基于图编码与小样本学习的分析诊断模型。该模型采用皮尔逊相关系数和自注意力机制构建自适应脑网络,并将时域特征、频域特征和脑网络特征作为图卷积神经网络的输入,进行动态学习自适应脑网络和图编码特征。将图编码特征作为图原型网络的输入,进行小样本学习并实现分类。将该模型应用于精神分裂症的分类诊断,实验结果表明,精神分裂症的识别准确率达到83.4%,为脑网络研究提供一种全新的思路和方法,为小样本学习在精神分裂症研究中的应用开辟了新的方向。
关键词:自适应脑网络;图编码特征;小样本学习;图原型网络;精神分裂症
中图分类号:TP391.4;TP18 文献标识码:A 文章编号: 2096-4706(2024)08-0123-05
DOI:10.19850/j.cnki.2096-4706.2024.08.027
0 引 言
精神分裂症是一种严重的精神疾病,通常表现为人格解体、思维混乱、幻觉、妄想以及情感和行为异常。这种疾病往往对患者的社交功能等方面产生负面影响。许多学者和研究人员对精神分裂症进行了深入的分析和研究,以做好对精神分裂症疾病的早期识别和干预,探寻有效的治疗方法等。
近年来,图神经网络(Graph Neural Network, GNN)、图卷积神经网络(Graph Convolutional Neural Network, GCN)和图注意力网络(Graph Attention Networks, GAT)等基于图论的网络[1-3]在结合信号数据进行疾病诊断、情绪识别等研究中取得良好成效。Chen等[4]基于脑区和连接性特征进行分析,并运用GCN对精神分裂症患者进行分类,该方法与传统机器学习和深度学习方法相比,有效提高了分类性能。Li等[5]首先将重度抑郁症患者每个EEG数据的多通道脑电信号拼接成一个信号序列,计算拼接信号之间的皮尔逊相关系数(Pearson Correlation Coefficient, PCC)形成图网络(脑网络)。其次将每个信道划分为六个频段,计算出每个频段的平均功率,并将它们拼接在一起作为节点特征。最后预训练GCN模型并微调输出层。该方法充分利用多通道EEG之间的交互,结合预训练提高对抑郁症患者的病症识别。Lei等[6]利用PCC构建脑网络,结合GCN研究精神分裂症患者功能性脑网络的拓扑异常,并确定对分类有重要作用的最显著区域。An等[7]提出基于EEG的2-way k-shot小样本学习网络对运动图像进行分类,该网络能够有效学习未知类别的代表性特征并对其进行合理的分类。其根据卷积、池化等操作对EEG的支持集和查询集进行跨频段特征提取和网络编码,再对已提取的特征进行注意力评分,同时根据k个支持特征的加权平均计算每个类别的代表向量,最后根据类别代表向量和查询特征预测关联分数,关联得分最大的类被预测为查询的标签。该网络结构虽然采用了小样本学习思想,但是其特征提取、网络构建、注意力机制评分和关联得分4个主要模块基本上都是采用卷积操作。该模型虽然操作单一,但却为基于度量的小样本学习与EEG的紧密结合开辟了新的思路。目前,基于小样本学习思想的研究在图像等领域较为常见,但应用于EEG的数据相对较少。基于度量方法[8]的小样本学习模型应用相对广泛,尤其是原型网络[9,10],且有较多的相关改进模型,然而,对于同种疾病的不同数据或不同疾病的不同数据,大部分基于图论模型的方法(如GNN、GCN、GAT等)在构建脑网络时所采用的功能连接指标不统一[11,12],且脑网络构建之后不再变化,甚至选择不同指标所得到的结果差异较大。除此之外,这类模型对数据量的依赖性较大,无法很好地区分未知疾病的数据。为此,本文提出一种基于图编码与小样本学习的分析诊断模型,并将其应用于精神分裂症的分类。首先利用PCC构建原始脑网络并结合自注意力机制[13]构建自适应脑网络,提取脑节点局部特征;然后将自适应脑网络作为邻接矩阵和脑节点局部特征输入GCN进行图编码特征的学习;最后再将图编码特征输入图原型网络(Graph encoding Prototype Network, GEPN)进行小样本学习并完成对精神分裂症的分类。将本文提出的模型在无自适应脑网络和少量数据情况下进行对比实验,并在精神分裂症数据集上对模型的分类性能进行评估。
1 基于图编码与小样本学习的模型框架
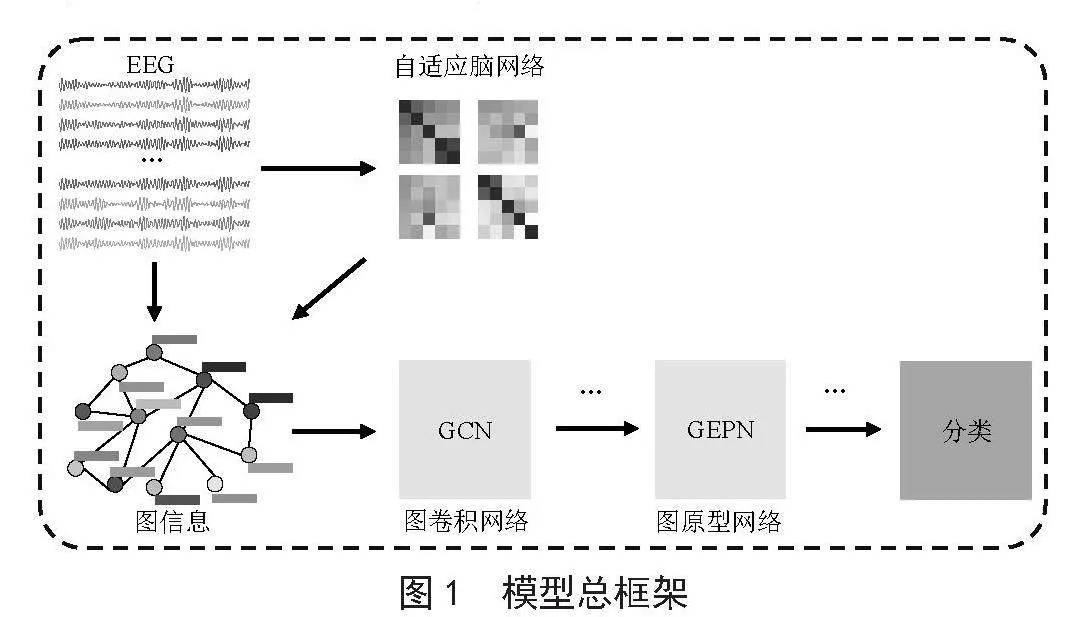
本文提出一种基于图编码与小样本学习的分析诊断模型,模型总框架如图1所示,主要包括四个部分,分别是:1)基于自注意力机制的自适应脑网络;2)基于GCN的图编码特征;3)划分图编码特征;4)基于GEPN的小样本学习。
1.1 基于自注意力机制的自适应脑网络
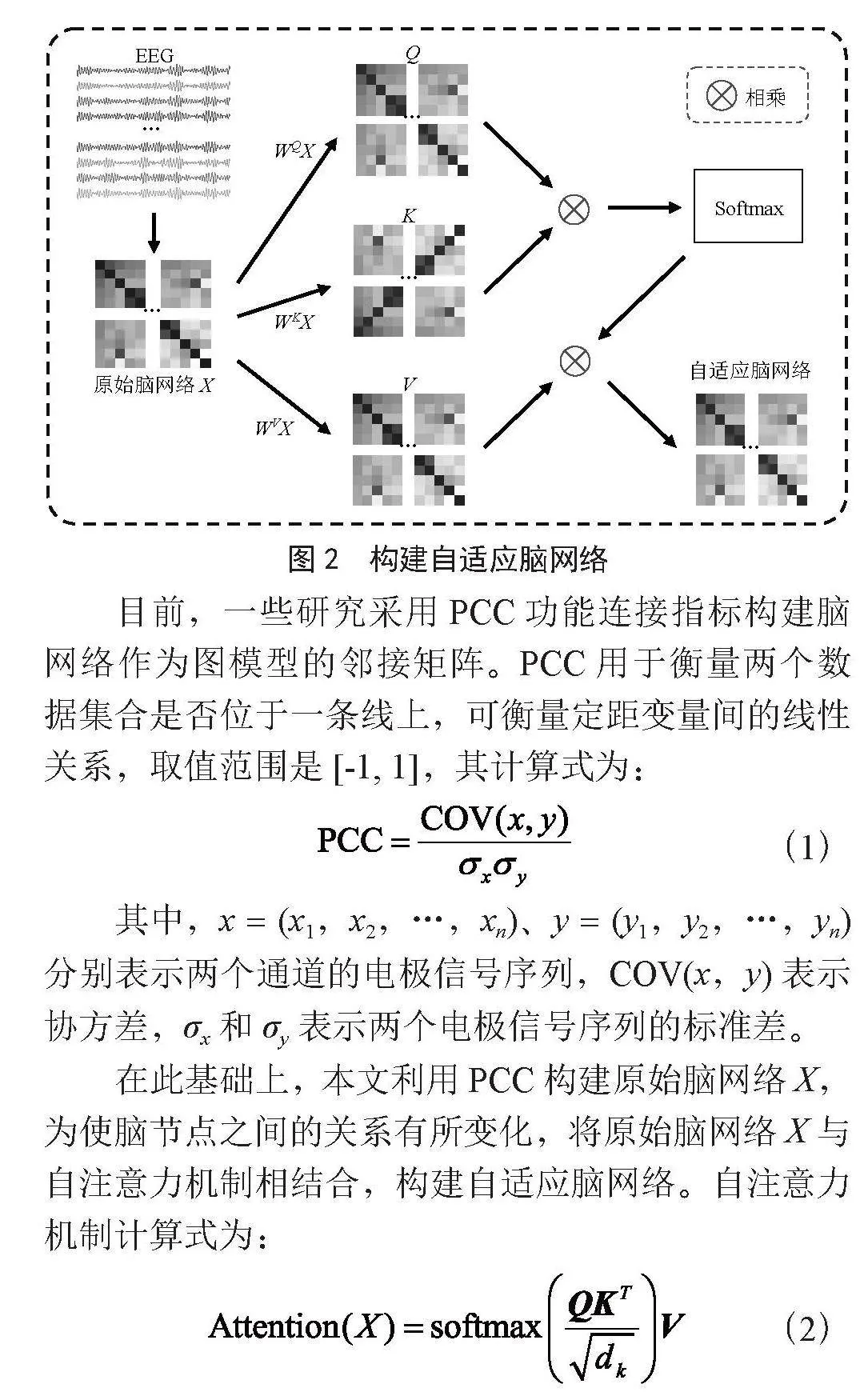
自适应脑网络构建过程如图2所示。
目前,一些研究采用PCC功能连接指标构建脑网络作为图模型的邻接矩阵。PCC用于衡量两个数据集合是否位于一条线上,可衡量定距变量间的线性关系,取值范围是[-1, 1],其计算式为:
(1)
其中,x = (x1,x2,…,xn)、y = (y1,y2,…,yn)分别表示两个通道的电极信号序列,COV(x,y)表示协方差,σx和σy表示两个电极信号序列的标准差。
在此基础上,本文利用PCC构建原始脑网络X,为使脑节点之间的关系有所变化,将原始脑网络X与自注意力机制相结合,构建自适应脑网络。自注意力机制计算式为:
(2)
其中,Q、K、V三个矩阵是由其对应的参数矩阵WQ、WK、WV与X相乘所得,dk表示脑节点通道维度。
1.2 基于GCN的图编码特征
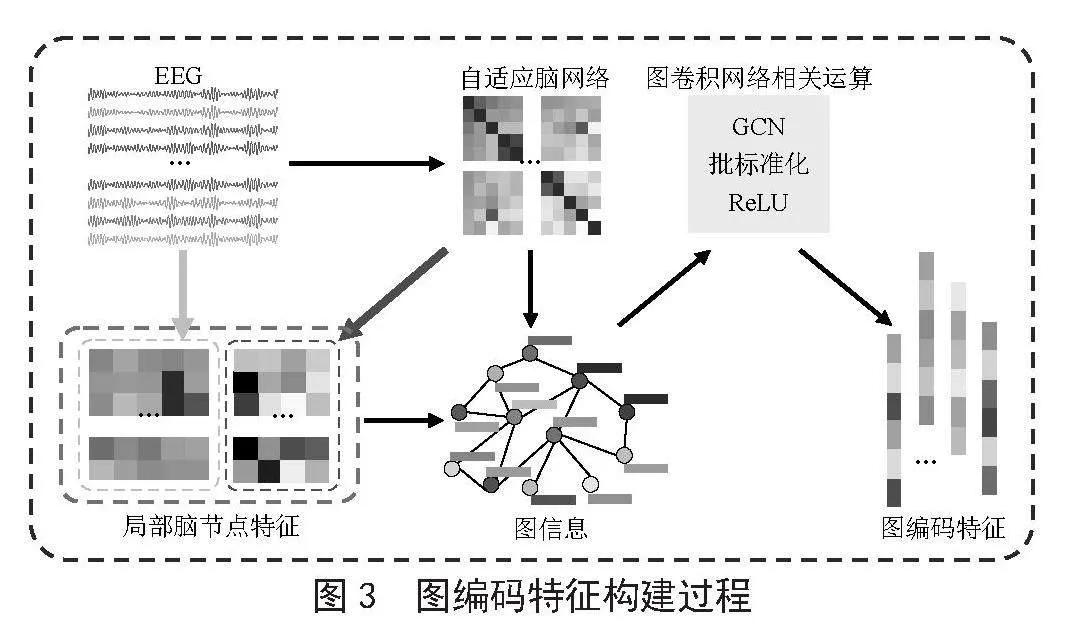
如图3所示为图编码特征的构建过程。
自适应脑网络的构建过程已在图2中有所展示,故图3中对该步骤进行了简化处理。
1.2.1 局部脑节点特征融合
首先,在处理好的EEG数据中提取脑节点的时域特征和频域特征[14]。其中,时域特征包括平均绝对值、方差、最小值、均方根、最大值、标准差、绝对标准偏差值、峰值、偏斜、峰度;频域特征包括功率谱密度,图2中的橙色虚线框为时域特征与频域特征的结合。
其次,在构建好自适应脑网络的基础上,从自适应脑网络中提取脑网络特征,脑网络特征随着自适应脑网络的变化而变化。其中,脑网络特征包括度中心性、节点介数、聚类系数、局部效率。提取脑网络特征时,选择步长2%和稀疏度范围20%~40%,计算该范围内每个脑节点的曲线下面积值作为脑网络特征,图3中的红色虚线框为脑网络特征。
最后,为了构建脑节点特征的多样性,将时域特征、频域特征和脑网络特征进行拼接融合,形成局部脑节点特征,图3中的绿色虚线框为融合特征。
1.2.2 图编码特征
利用GCN学习图编码特征,本文采用无向完全图并且将自环关系考虑在内。将融合后的局部脑节点特征作为GCN图信息中的结点特征,将所构建的自适应脑网络作为GCN图信息中的邻接矩阵。GCN中卷积层的运算式为:
(3)
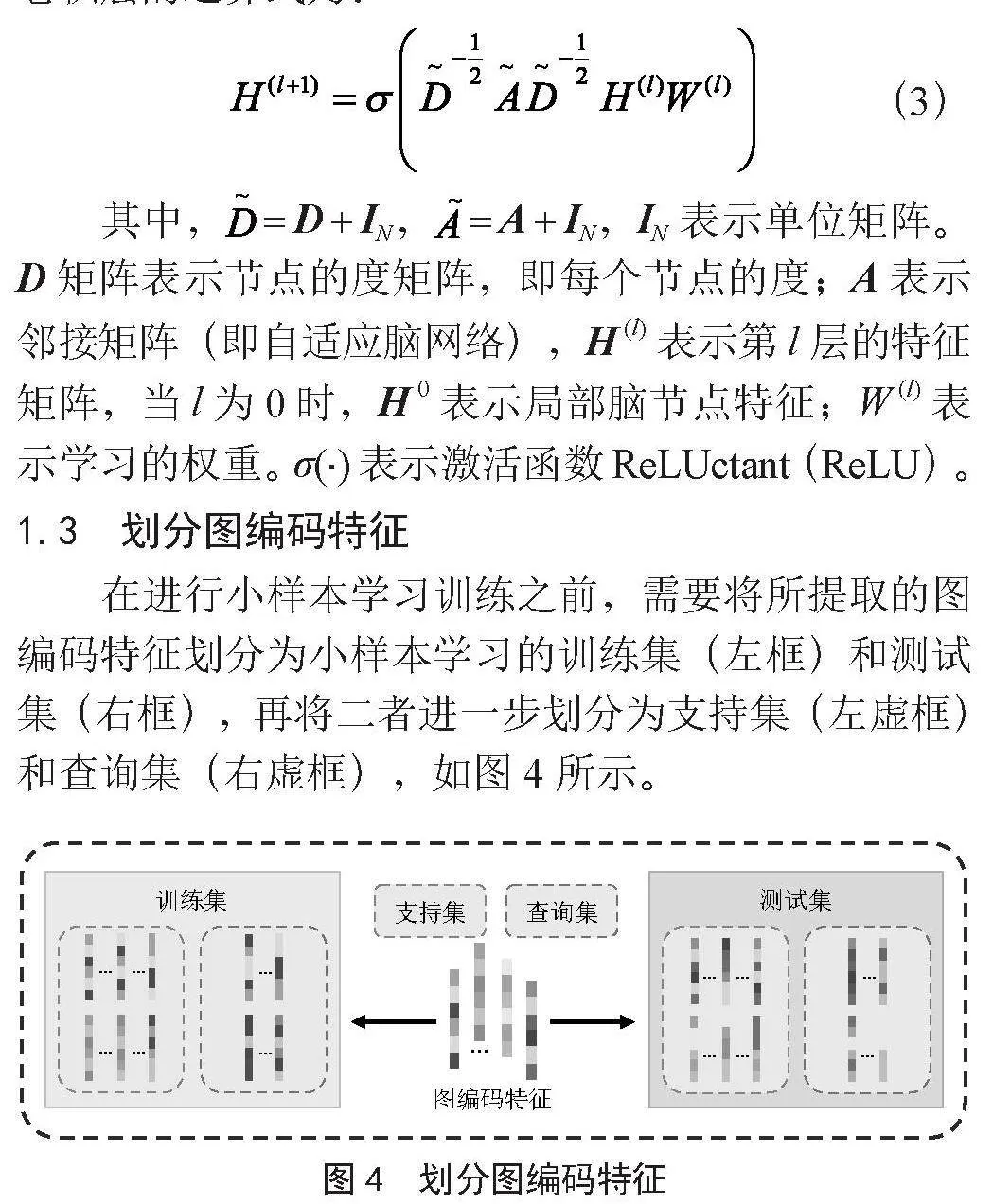
其中, = D + IN, = A + IN,IN表示单位矩阵。D矩阵表示节点的度矩阵,即每个节点的度;A表示邻接矩阵(即自适应脑网络),H (l)表示第l层的特征矩阵,当l为0时,H 0表示局部脑节点特征;W (l)表示学习的权重。σ(∙)表示激活函数ReLUctant(ReLU)。
1.3 划分图编码特征
在进行小样本学习训练之前,需要将所提取的图编码特征划分为小样本学习的训练集(左框)和测试集(右框),再将二者进一步划分为支持集(左虚框)和查询集(右虚框),如图4所示。
将全部数据按照一定的比例划分为GCN的训练集和测试集,按照上述过程进行GCN分类,当分类准确率达到70%时,保存其全连层的结果作为图编码特征。再根据实验需求划分为小样本学习的训练集和测试集图编码特征,作为后续小样本学习的训练输入。
1.4 基于GEPN的小样本学习
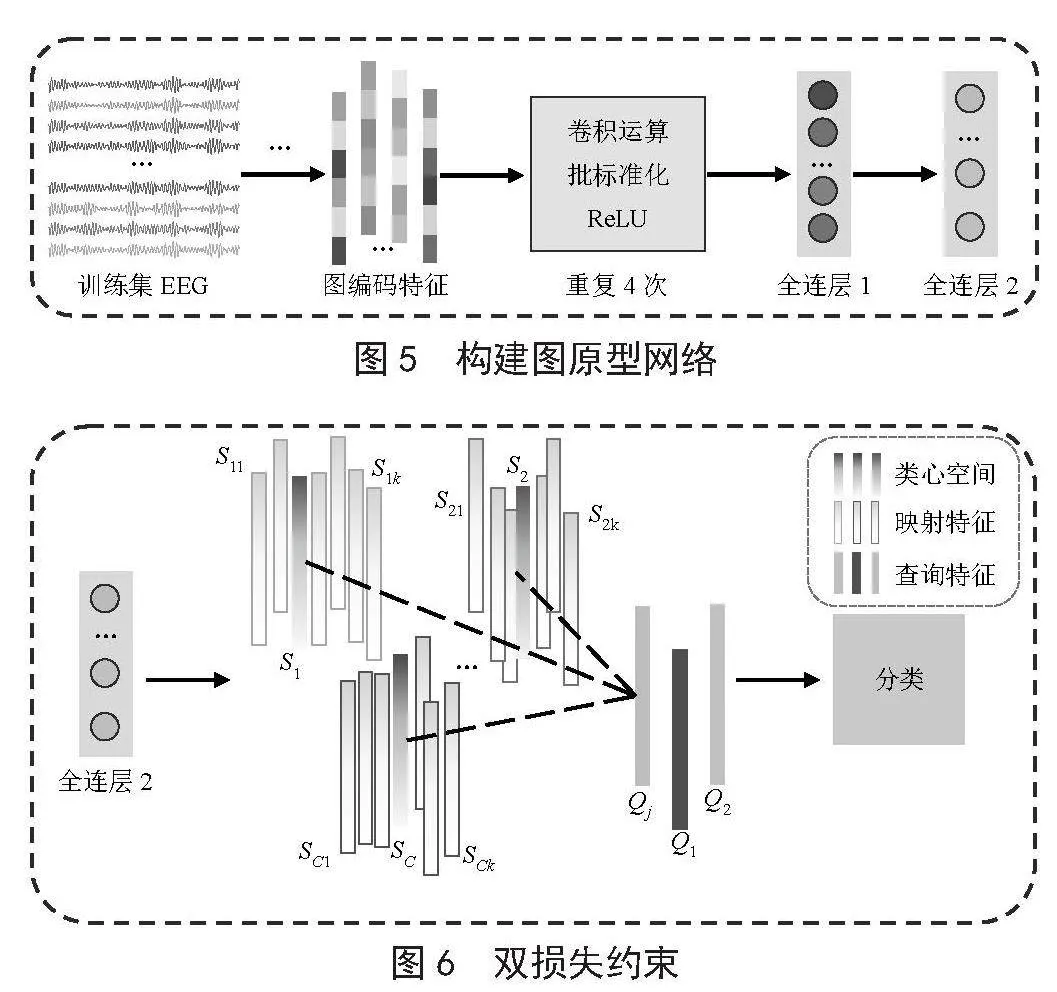
获取图编码特征后,将图编码特征作为GEPN的输入,经过全连层输出映射特征,并根据映射特征进行双损失约束训练,GEPN的构建过程和双损失约束如图5和图6所示。其中,构建自适应脑网络、图编码特征的详细过程已在图2和图3中予以展示,故图5中对该步骤进行了简化处理。
1.4.1 构建GEPN
在GEPN中,首先将所获取的图编码特征依次经过卷积运算、批标准化运算和ReLU激活函数映射并重复4次,然后运用两个全连层进行映射,最后进行分类训练和预测。其中,卷积运算的卷积核维度均为1×1。
1.4.2 双损失约束
在普通的网络中,经过全连层之后会直接进行概率计算进而进行分类的判断。GEPN则有所不同,GEPN是根据查询集进行分类效果的判断。GEPN通过双损失函数对模型进行约束,需要确保同类别之间的映射特征空间距离其“类心空间”较小,不同类别之间的映射特征空间距离其“类心空间”较大。
如图6所示,进行模型训练时,首先,将训练集中支持集和查询集的每个数据输入到网络中(经过全连层2之后,每个数据可得到最终的“映射特征”);其次,根据加权平均计算,进而算出同类别支持集的“映射特征”SCi的“类心空间”SC;再次,最大化不同“类心空间”SC的距离作为模型训练的第一个损失,即Loss1;最后,计算查询集中每个数据“查询特征”Qj到多个“类心空间”SC的距离,即Loss2(每个查询数据所属类别为离它最近的“类心空间”所属的类别,即最大概率的类别)。测试模型时,也需要使用支持集和查询集,除了参数不更新外,其他过程一样。
Loss1表示均方误差损失函数,Loss2表示交叉熵损失函数。yjc表示当前观察样本数据是否为其真实类别,当“查询特征”Qj属于其真实类别C时,yjc为1,否则为0;Pjc表示当前观察样本数据j属于类别C的预测概率,即“查询特征”Qj预测为真实类别的概率;k表示每个类别的样本数量。因此,模型训练的总损失可表示为:
(4)
2 实验与分析
2.1 数据说明
本文实验选用的数据为UMN数据库[15-17]的静息态EEG公共数据集,分别为强迫症数据集、抑郁症数据集、帕金森数据集,三个数据集的电极都超过64个;还有从北京回龙观医院采集的精神分裂症患者及其健康被试的静息态EEG数据集,数据均有59个电极。
2.2 数据预处理
不同的数据之间可能存在噪声和量纲上的差异,因此,先对每个数据进行500 Hz频率的采样,接着用EEGLAB剔除眼电等异常数据并删除坏段,然后将数据按照每个通道(电极)进行标准化,最后选择40秒到200秒之间的数据段。为了使不同数据的通道相同,本文采用56个相同的通道进行实验。
2.3 实验设计
本文中的EEG数据有56个脑节点(即56个通道),故最终构建的自适应脑网络维度为56×56,每个通道数据的长度均为160 s,采样频率为500 Hz,每个脑节点有15个特征。
在进行小样本学习之前,将预处理后数据的70%作为训练集,30%作为测试集,再通过GCN进行分类,当测试集的分类准确率达到70%时,提取出全连层所得结果作为图编码特征。将图编码特征分为训练集图编码特征和测试集图编码特征,训练集和测试集中都包含支持集图编码特征和查询集图编码特征。
采用3-way k-shot进行小样本学习训练,其中,3表示训练集图编码特征类别数量,即强迫症、抑郁症和帕金森,k表示小样本学习中每个类别的数量,可取3、5、10,即支持集在3个类别中随机选择k个数据进行学习,将其余的同类数据作为查询集进行验证。采用2-way k-shot进行测试,2表示测试集包括精神分裂症患者及其健康被试两个类别数据图编码特征,k表示这两个类别的支持集图编码特征的数量,与训练时保持一致,即训练和测试的k值一样。
2.4 实验评估指标
本文提出的模型采用不同的评估指标,分别有:正确率(Accuracy),表示正确分类的样本数占总样本数的比例;精确率(Precision),表示正确预测为正例的样本数占预测为正例样本数的比例;召回率(Recall),表示正确预测为正例的样本数占实际为正例样本数的比例;F1分数(F1-Score),表示综合考虑精确率和召回率的平衡性,是精确率和召回率的调和平均值。计算式分别如(5)至(8)所示:
(5)
(6)
(7)
(8)
其中,TP表示真正例(True Positive),即预测和真实均为精神分裂症患者;TN表示真负例(True Negative),即预测为精神分裂症患者,真实为健康被试;FP表示假正例(False Positive),即预测和真实均为健康被试;FN表示假负例(False Negative),即预测为健康被试,真实为精神分裂症患者。
2.5 实验结果分析与结论
k分别取3、5、10进行训练和测试,其评估指标如表1所示。
由表1可知,随着k值的增加(即每个类别训练样本和测试样本的增加),4个指标都有所提高。当k为10即每个类别的支持集为10个样本时,其正确率、精确率、召回率、F1分数都为最高,分别为0.834 3、0.932 4、0.741 9、0.826 3。实验结果表明,本文提出的基于图编码与小样本学习的分析诊断模型在样本数据很少的情况下仍可以很好地完成精神分裂症患者的判别,为那些想要在样本数据缺失情况下获得较高精神分裂症分类准确率的研究人员提供参考。
3 结 论
本文针对图论神经网络构建脑网络后不再变化以及对数据量的依赖问题,提出一种基于图编码与小样本学习的分析诊断模型。通过自注意力机制构建自适应脑网络来解决脑网络不变的问题,构建GCN提取图编码特征和对GEPN进行分类,缓解了深度学习网络对数据的依赖,解决了未见过数据的分类问题,泛化能力较强。实验结果证明了本文所提模型的有效性,在未来的工作中将继续利用其他图论网络和其他基于度量的小样本学习方式进行实验。
参考文献:
[1] LI Z J,ZHANG G Y,WANG L B,et al. Emotion Recognition Using Spatial-temporal EEG Features through Convolutional Graph Attention Network [J/OL].https://iopscience.iop.org/article/10.1088/1741-2552/acb79e.
[2] ZHU C,TAN Y,YANG S Q,et al. Temporal Dynamic Synchronous Functional Brain Network for Schizophrenia Diagnosis and Lateralization Analysis [J/OL]. arXiv:2304.01347v4 [q-bio.NC].[2023-07-23].https://arxiv.org/abs/2304.01347.
[3] ZHU Y Q,CUI H J,HE L F,et al. Joint Embedding of Structural and Functional Brain Networks with Graph Neural Networks for Mental Illness Diagnosis [J/OL].Annual International Conference of the IEEE Engineering in Medicine and Biology Society,2022[2023-08-05].https://pubmed.ncbi.nlm.nih.gov/36085703/.
[4] CHEN X Y,ZHOU J,KE P F,et al. Classification of Schizophrenia Patients Using a Graph Convolutional Network: A Combined Functional MRI and Connectomics Analysis [J/OL].https://doi.org/10.1016/j.bspc.2022.104293.
[5] LI W,WANG H,ZHUANG L H,et al. GCNS-MI: EEG Recognition of Depression Based on Graph Mutual Information Maximization [EB/OL].[2023-07-09].https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4000327Available at SSRN 4000327.
[6] LEI D,QIN K,PINAYA W H L,et al. Graph Convolutional Networks Reveal Network-level Functional Dysconnectivity in Schizophrenia [J].Schizophrenia Bulletin,2022,48(4):881-892.
[7] AN S,KIM S,CHIKONTWE P,et al. Few-shot Relation Learning with Attention for EEG-based Motor Imagery Classification [C]//2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Las Vegas:IEEE,2020:10933-10938.
[8] CRISOSTOMI D,ANTONELLI S,MAIORCA V,et al. Metric Based Few-Shot Graph Classification [EB/OL].[2023-07-06].https://proceedings.mlr.press/v198/crisostomi22a.
[9] SNELL J,SWERSKY K,ZEMEL R. Prototypical Networks for Few-shot Learning [C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. [S.l.]:Curran Associates Inc.,2017:4080-4090.
[10] GAO Y K,LIU A P,WANG L L,et al. A Self-Interpretable Deep Learning Model for Seizure Prediction Using a Multi-Scale Prototypical Part Network [J].IEEE Transactions on Neural Systems and Rehabilitation Engineering,2023,31:1847-1856.
[11] HU J L,CAO L J,LI T H,et al. GAT-LI: a Graph Attention Network Based Learning and Interpreting Method for Functional Brain Network Classification [J].BMC Bioinformatics,2021,22(1):1-20.
[12] POLAT H. Brain Functional Connectivity Based on Phase Lag Index of Electroencephalography for Automated Diagnosis of Schizophrenia Using Residual Neural Networks [J/OL].Journal of Applied Clinical Medical Physics,2023,24(7)[2023-07-20].https://doi.org/10.1002/acm2.14039.
[13] SHEN L,SUN M,LI Q,et al. Multiscale Temporal Self-attention and Dynamical Graph Convolution Hybrid Network for EEG-based Stereogram Recognition [J/OL].arXiv:2302.10428v1 [cs.LG].[2023-07-20].https://arxiv.org/pdf/2302.10428.pdf.
[14] 张格,林岚,吴水才.基于脑网络的图卷积神经网络在脑疾病中的研究进展 [J].医疗卫生装备,2021,42(8):85-92.
[15] ALBRECHT M A,WALTZ J A,CAVANAGH J F,et al. Increased Conflict-induced Slowing, But No Differences in Conflict-induced Positive or Negative Prediction Error Learning in Patients with schizophrenia [J].Neuropsychologia,2018,123:131-140.
[16] CAVANAGH J F,BISMARK A W,FRANK M J,et al. Multiple Dissociations between Comorbid Depression and Anxiety on Reward and Punishment Processing: Evidence from Computationally Informed EEG [J].Computational Psychiatry,2019,3:1-17.
[17] GRüNDLER T O J,CAVANAGH J F,FIGUEROA C M,et al. Task-related Dissociation in ERN Amplitude as a Function of Obsessive–compulsive Symptoms [J].Neuropsychologia,2009,47(8-9):1978-1987.
作者简介:符永灿(1997—),男,汉族,广东广州人,硕士研究生在读,研究方向:智能数据分析与应用。
收稿日期:2023-09-20
A Method for Analyzing Schizophrenia Based on Graph Encoding and Few-Shot Learning
FU Yongchan, YIN Guimei, SHENG Zhilin
(College of Computer Science and Technology, Taiyuan Normal University, Jinzhong 030619, China)
Abstract: In research on functional brain diseases based on graph neural networks, the constructed brain networks remain static and typically require a large amount of data for modeling and training. To address these two problems, this paper proposes an analysis and diagnostic model based on graph encoding and Few-shot learning. The model utilizes Pearson correlation coefficient and Self-Attention mechanism to construct an adaptive brain network, and takes temporal features, frequency domain features, and brain network features as inputs to a graph convolutional neural network, thereby dynamically learning the adaptive brain network and graph encoding features. The graph encoding features are used as inputs to a graph prototype network for Few-shot learning and classification. Applying this model to the classification and diagnosis of schizophrenia, experimental results demonstrate an accuracy rate of 83.4% in schizophrenia identification. This provides a novel perspective and approach for brain network research, and opens up new directions for the application of Few-shot learning in schizophrenia studies.
Keywords: adaptive brain network; graph encoding feature; Few-Shot Learning; graph prototype network; schizophrenia