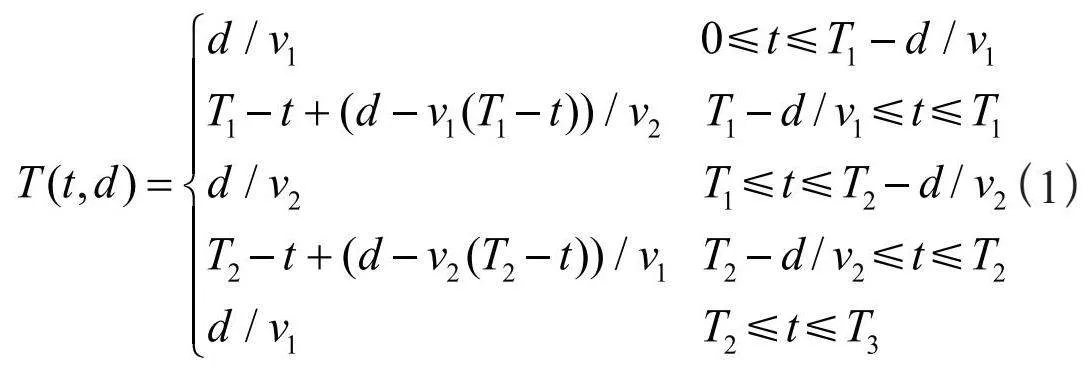

摘" 要:在人口稠密城区的卡车—无人机协同配送场景中,设计人员在设计已有配送路径规划模式时粗略地认为卡车的行驶速度恒定不变,但随着城市交通日益拥堵,卡车的行驶速度产生时变性。考虑到城区实际交通环境下卡车速度的时变性,对卡车和无人机的协同配送路径的建模进行分析。在分析问题根源的基础上,分别从模型假设、目标函数及约束条件等方面进行了探讨。
关键词:卡车—无人机协同配送;无人机配送;时变;路径优化;建模
中图分类号:TP391;U491" " 文献标识码:A" 文章编号:2096-4706(2024)09-0110-04
Research on the Modeling of Time-varying Truck and Drone Collaborative Delivery Path
ZOU Ye
(Hunan University of Technology and Business, Changsha" 410205, China)
Abstract: In the collaborative truck and drone delivery scenario in densely populated urban areas, designers roughly assume that the speed of trucks remains constant when designing existing delivery path planning mode. However, as urban traffic becomes increasingly congested, the speed of trucks varies over time. Considering the time-varying speed of trucks in the actual transportation environment of urban areas, analyze the modeling of collaborative truck and drone delivery paths. On the basis of analyzing the root cause of the problem, discussions are conducted from the perspectives of model assumptions, objective functions, and constraints.
Keywords: collaborative truck and drone delivery; drone delivery; time-varying; path optimization; modeling
0" 引" 言
无人机物流行业在迅速发展的同时面临着巨大的运营管理挑战。因此,如何在时变行驶速度的情形下规划卡车—无人机协同配送路径以最大限度缩短服务时间,这是无人机物流企业亟待解决的运营问题。本文主要研究基于时变卡车速度的卡车—无人机协同配送路径优化模型。
1" 国内外研究现状
近年来,卡车—无人机协同配送问题成为国内外的研究热点。无人机配送具有成本低、速度快以及飞行不受地面交通限制等优点,但其续航里程短、载重量有限、飞行安全性低。相反,卡车配送具有续航里程长、载重量大等优点,但成本高、速度慢、受地面交通限制。结合无人机配送和卡车配送的特点,国内外出现很多关于卡车—无人机协同配送问题的研究。例如,Vásquez等[1]针对基于无人机的旅行商问题构建了优化模型,决策由卡车服务的客户子集并对客户进行排序,同时决策无人机服务每个剩余客户的派遣以及收集位置。Yurek等[2]以最小化配送完成时间为目标,优化单卡车—单无人机的协同配送路径,在迭代算法中首先确定卡车路径和分配给无人机的客户,然后求解无人机路径优化的混合整数线性规划模型。郭秀萍等[3]在单卡车—单无人机的协同配送路径规划研究中充分考虑了无人机电量约束和载重量约束问题。
此外,考虑到无人机一次可运送多个包裹及服务多个客户,Poikonen等[4]研究了单卡车+多无人机的协同配送问题。Murray等[5]研究了卡车—无人机协同配送的两种混合整数线性规划模型,前者假设无人机由卡车进行派送和收集,后者假设无人机由配送中心进行派送和收集,且卡车和无人机的配送路径相对独立。Moshref-Javadi等[6]以客户等待时间最小化为目标,构建了单卡车+多无人机协同配送路径优化模型,以确定客户集合在卡车和无人机之间的最优分配、最优卡车路径,以及无人机沿卡车路径的最优发射和收集位置。Salama等[7]研究单卡车+多无人机协同配送问题,将客户划分为小集群,每个集群确定一个焦点,并假设集群焦点可位于其中一个客户位置或任一配送位置。构建优化模型并设计基于无监督机器学习的启发式算法。Dell´Amico等[8]以最小化服务时间为目标,构建了无人机和车辆并行配送优化模型。Saleu等[9]研究最小化配送时间的单卡车与无人机并行配送路径优化,卡车执行传统送货路径,而无人机执行往返路径,并提出迭代两步启发式算法,其中包括将问题转换为客户序列的编码步骤,以及将客户序列分解为车辆路径和无人机路径的解码步骤。Ha等[10]以最小化运输成本和车辆等待时间成本为目标,研究单卡车+多无人机协同配送路径问题,并提出两种算法:第一种算法通过局部搜索将最优TSP解转化为可行解。第二种算法是贪婪随机自适应搜索过程,它基于一个新的分割过程,将任意TSP路径最优地分割为问题解,通过局部搜索算子对问题解进行改进。Agatz等[11]研究单卡车+多无人机协同配送路径问题,构建优化模型并基于局部搜索和动态规划设计几种先路径、后聚类的启发式算法。
综上分析可知,大多数卡车—无人机协同配送模式并未涉及卡车的时变速度,这不符合城市交通日益拥堵的现实场景。本文在优化卡车—无人机的协同配送路径时将卡车的时变速度考虑在内。
2" 时变卡车速度
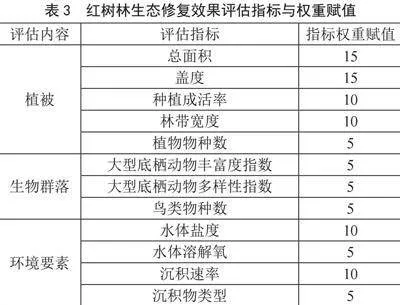
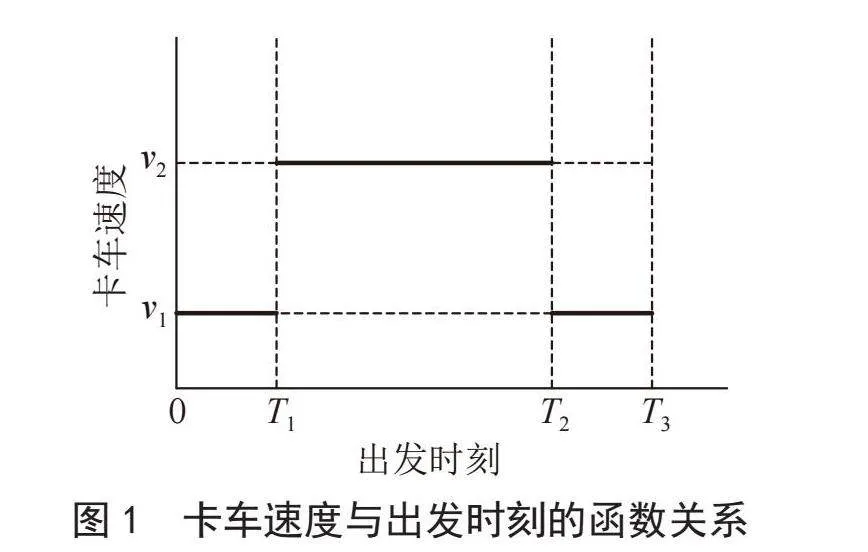
卡车速度因受城市交通拥堵状况的影响而具有时变性。卡车速度取决于出发时刻,假设二者之间的函数关系为阶梯函数[12],如图1所示。
由图1可知,时段[0,T1]和时段[T2,T3]分别为早高峰时段和晚高峰时段,此时卡车速度均为v1;时段[T1,T2]为非高峰时段,此时卡车速度为v2,且v2>v1。卡车在t时刻出发完成距离为d的路段所需的行驶时间T(t,d)的计算式为:
(1)
3" 问题描述
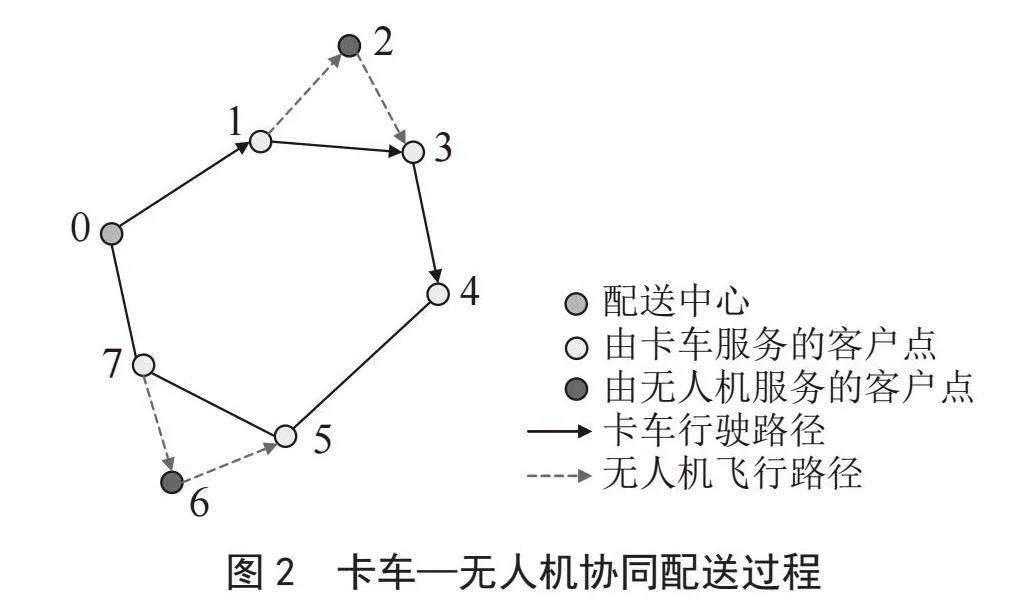
本文研究基于时变卡车速度的卡车—无人机协同配送路径问题,在Murray等[5]所提出FSTSP问题的基本假设上考虑卡车的时变速度,其配送过程如图2所示[13]。一辆卡车携带一架无人机从配送中心0出发,服务客户点1并发射无人机,在等待无人机返回过程中服务客户点3并收集无人机,然后服务客户点4和客户点5并在客户点5发射无人机,在等待无人机返回过程中服务客户点7并收集无人机,最后返回配送中心,其间无人机在两次行程中分别服务了客户点2和客户点6 [13]。卡车的速度依赖于出发时间,因而影响客户服务时间,且在城市拥堵高峰时段出发时的卡车速度小于其余时段出发时的卡车速度。
图2" 卡车—无人机协同配送过程
在卡车—无人机协同配送过程中,每个客户必须被无人机或卡车服务一次。值得注意的是,客户在某些情形下不能被无人机服务,例如,当出现包裹重量超过了无人机的额定载重量、包裹需要客户签字、客户所在位置无法使无人机安全着陆等情况时,这些包裹只能由卡车服务。
卡车和无人机只能从配送中心协同或单独出发一次,协同或单独返回配送中心一次。在一次配送的过程中,无人机会飞行多个架次,每个架次由三个节点组成。第一个节点为无人机出发节点,无人机可直接从配送中心出发,也可从某客户点出发。若从客户点出发,卡车司机负责替换无人机电池并将包裹装载至无人机。第二个节点为无人机所服务的客户节点。第三个节点为无人机返回节点,无人机可直接返回配送中心,也可返回卡车所在的客户节点。若返回至卡车所在的客户节点,卡车司机负责将无人机装载至卡车上。无人机一旦起飞,必须在其续航里程之内完成整个架次。本文研究的卡车—无人机协同配送的目标为最小化配送服务时间。
4" 模型假设条件
考虑时变卡车速度的卡车—无人机协同配送问题假设如下:
1)无人机在一个架次中只服务一个客户,而卡车在无人机飞行一个架次的期间内能服务多个客户。
2)除了服务客户时,无人机在一个架次中始终保持飞行状态,且当无人机和卡车汇合时,即使无人机先于卡车到达,无人机也不能临时着陆。
3)若无人机和卡车汇合于某客户节点i,无人机可直接从i起飞开启下一个架次的飞行。但若无人机从i起飞,那么它不能与卡车汇合于节点i。
4)若无人机与卡车汇合,则只能汇合于由卡车服务的某个客户节点,且不能在路线的某个点上与卡车汇合,同时卡车不能通过多次访问客户节点来回收无人机。
5)除配送中心外,卡车和无人机均不能访问任何非客户节点,且均不能多次访问客户。
6)无人机架次若结束于配送中心,即无人机和卡车单独返回配送中心,那么无人机不可再次从配送中心起飞,亦即无人机不再提供配送服务。值得注意的是,正是由于无人机存在续航里程、载重量等限制,故产生了卡车协助无人机进行配送的运营模式,故该假设与问题背景是相符的。
5" 模型目标函数和约束条件
针对考虑时变卡车速度的卡车—无人机协同配送问题,构建混合整数线性规划模型。C = {1,2,…,c}表示所有客户的集合,C′ ⊆ C表示C中可能会被无人机服务的客户子集。0和c+1表示同一个配送中心的起始点和返回点,即无人机和卡车从0出发,并返回c+1。由此,N = {0,1,…,c+1}表示配送网络中所有节点的集合,N0 = {0,1,…,c}表示无人机和卡车可能的出发节点集合,N+ = {1,…,c+1}表示无人机和卡车可能的到达节点集合。dij、τij分别表示卡车从节点i ∈ N0到节点j ∈ N+的行驶距离和时间, 表示无人机从节点i ∈ N0到节点j ∈ N+的行驶时间。sL表示卡车司机替换无人机电池并将包裹装载至无人机的时间,即为无人机起飞准备工作的时间。sR表示卡车司机回收无人机的时间。e表示以时间单位表示的无人机续航时间。P表示无人机可能执行的所有三节点架次lt;i,j,kgt;的集合,该架次lt;i,j,kgt;必须满足如下条件:
1)无人机架次lt;i,j,kgt;的起飞节点i不能是配送中心结束节点c+1,即i ∈ N0。
2)无人机架次lt;i,j,kgt;的配送节点j必须是无人机可服务的某客户点,且节点j不能与起飞节点i相同,即j ∈ {C′: j ≠ i}。
3)无人机架次lt;i,j,kgt;的汇合节点k为客户点或配送中心结束节点c+1,且节点k不能与节点i和j相同,无人机遍历i→j→k的路径飞行时间不能超过无人机的额定续航时间,即 。
决策变量如下:
其中,tj表示卡车到达节点j ( j ∈ N+)的时间,tj≥0; 表示无人机到达节点j ( j ∈ N+)的时间,≥0。另外,设置两个辅助决策变量如下:
其中,ui表示节点i (i ∈ N)在卡车路径中的位置,1≤ui≤c+2。
目标函数为最小化配送服务时间,约束条件如下:
1)卡车从配送中心出发并最终返回配送中心。
2)每个顾客必须被卡车或无人机服务一次。
3)对卡车路径上的每个客户节点而言,卡车将到达该节点并离开该节点。
4)无人机的每个起飞节点至多发射一次无人机。
5)无人机的每个回收节点至多回收一次无人机。
6)若无人机执行了某架次,卡车必然经过该架次的起飞节点和回收节点。
7)若无人机执行了某架次,无人机和卡车必须同时到达该架次的起飞节点。
8)若无人机执行了某架次,无人机和卡车必须同时到达该架次的结束节点。
9)在卡车路径中,卡车到达两个相邻节点的时间关系:即卡车到达后一节点的时间为卡车到达前一节点的时间加上两节点之间的卡车行驶时间,再加上卡车在后一节点回收无人机以及发射无人机的时间。
10)在一个无人机架次中,无人机到达客户节点的时间为无人机到达起飞节点的时间加上起飞节点和客户节点之间的飞行时间。
11)在一个无人机架次中,无人机到达回收节点的时间为无人机到达客户节点的时间加上客户节点与回收节点之间的飞行时间,再加上无人机的回收时间。
12)在一个无人机架次中,无人机的飞行时间不能超过其额定的续航时间。
13)卡车子路径消除约束。
14)在卡车路径中客户节点的先后服务顺序之间的关系。
15)卡车先从配送中心出发再服务客户。
16)无人机在某个架次的回收节点与在某个架次的发射节点的到达时间之间的关系。
17)无人机和卡车均于0时刻在配送中心出发。
18)决策变量的0—1约束。
19)决策变量的非负约束。
20)辅助决策变量的0—1约束。
21)卡车路径上节点位置序号的约束。
6" 结" 论
在卡车—无人机协同配送服务网络中,研究考虑时变卡车速度的卡车—无人机协同配送路径优化模型,更符合实际运营场景,在一定程度上丰富了现有的研究体系,并为物流企业的无人机配送路径决策提供参考,提高配送效率和企业利润,进一步加快了物流行业节能减碳的进程。
参考文献:
[1] VÁSQUEZ S A,ANGULO G,KLAPP M A. An Exact Solution Method for the TSP with Drone Based on Decomposition [J/OL].Computers amp; Operations Research,2021,127[2023-09-13].https://doi.org/10.1016/j.cor.2020.105127.
[2] YUREK E E,OZMUTLU H C. A Decomposition-based Iterative Optimization Algorithm for Traveling Salesman Problem with Drone [J].Transportation Research Part C: Emerging Technologies,2018,91:249-262.
[3] 郭秀萍,胡运霞.卡车与无人机联合配送模式下物流调度的优化研究 [J].工业工程与管理,2021,26(1):1-8.
[4] POIKONEN S,GOLDEN B. Multi-visit Drone Routing Problem [J/OL].Computers amp; Operations Research,2020,113[2023-09-15].https://doi.org/10.1016/j.cor.2019.104802.
[5] MURRAY C C,CHU A G. The Flying Sidekick Traveling Salesman Problem: Optimization of Drone-assisted Parcel Delivery [J].Transportation Research Part C: Emerging Technologies,2015,54:86-109.
[6] MOSHREF-JAVADI M,HEMMATI A,WINKENBACH M. A Truck and Drones Model for Last-mile Delivery: A Mathematical Model and Heuristic Approach [J].Applied Mathematical Modelling,2020,80:290-318.
[7] SALAMA M,SRINIVAS S. Joint Optimization of Customer Location Clustering and Drone-based Routing for Last-mile Deliveries [J].Transportation Research Part C: Emerging Technologies,2020,114:620-642.
[8] DELL´AMICO M,MONTEMANNI R,NOVELLANI S. Matheuristic Algorithms for the Parallel Drone Scheduling Traveling Salesman Problem [J].Annals of Operations Research,2020,289:211-226.
[9] SALEU R G M,DEROUSSI L,FEILLET D,et al. An Iterative Two-step Heuristic for the Parallel Drone Scheduling Traveling Salesman Problem [J].Networks,2018,72(4):459-474.
[10] HA Q M,DEVILLE Y,PHAM Q D,et al. On the min-cost Traveling Salesman Problem with Drone [J].Transportation Research Part C: Emerging Technologies,2018,86:597-621.
[11] AGATZ N,BOUMAN P,SCHMIDT M. Optimization Approaches for the Traveling Salesman Problem with Drone [J].Transportation science,2018,52(4):965-981.
[12] MA B S,HU D W,WANG Y,et al. Time-dependent Vehicle Routing Problem with Departure Time and Speed Optimization for Shared Autonomous Electric Vehicle Service [J].Applied Mathematical Modelling,2023,113:333-357.
[13] 宋佳怡,毛瑜琳,艾云艳,等.无人机配送问题研究综述 [J].现代信息科技,2023,7(8):146-150.
作者简介:邹晔(1991—),女,汉族,湖南益阳人,讲师,博士,研究方向:组合优化问题。