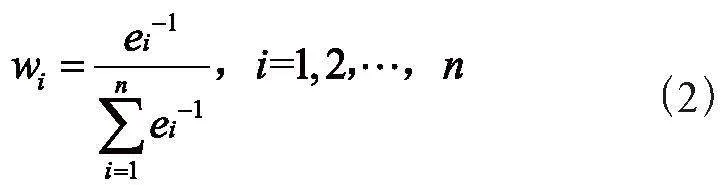

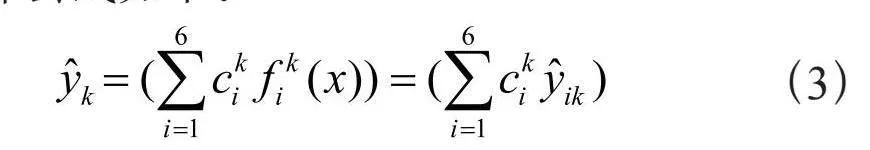
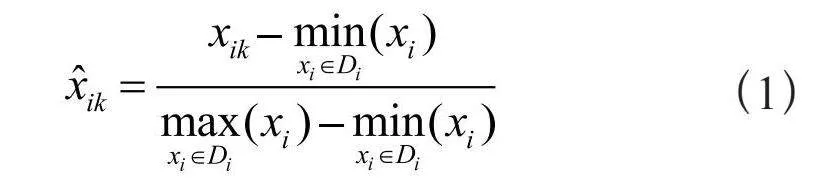
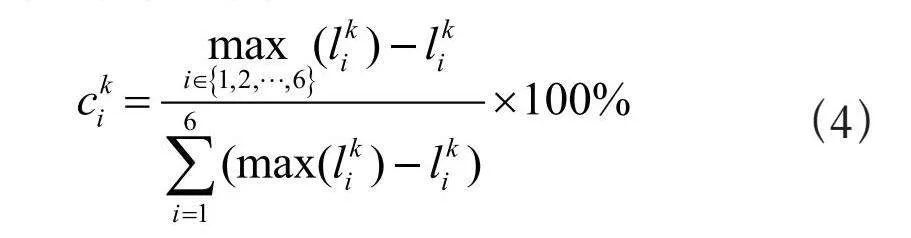
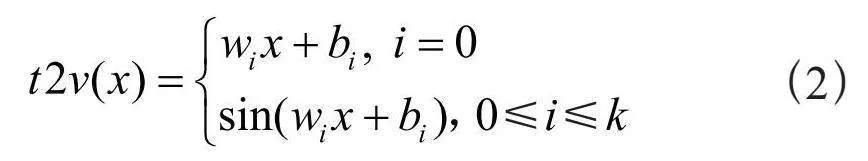
摘" 要:股票市场是国民经济的一个重要组成部分,股票投资是一项高风险但同时高回报的投资方式。为了给股票投资者提供参考,对未来股票价格进行了预测研究。设计了一种基于深度学习的集成预测算法,对未来5日的股价进行预测。研究结果显示,基于预测性能的权重分配集成方法相比基本模型平均绝对误差(MAE)降低,在平均绝对误差评价指标上给出了最好的结果。
关键词:深度学习;股价预测;集成学习
中图分类号:TP18" 文献标识码:A" " " 文章编号:2096-4706(2024)09-0114-06
Stock Price Prediction Based on Integrated Deep Learning
GUO Huiting, CHANG Yanzhen, LI Liang, XU Yongli
(Beijing University of Chemical Technology, Beijing" 100029, China)
Abstract: The stock market is an important component of the national economy, and stock investment is a high-risk but high-return investment method. To provide guidance for stock investors, a research is conducted to predict future stock prices. This paper designs an integrated prediction algorithm based on Deep Learning for predicting the stock price over the next 5 days. The research results show that the MAE of the weight allocation integrated method based on prediction performance reduces compared to the basic model and gives the best results on MAE index.
Keywords: Deep Learning; stock price prediction; integrated learning
0" 引" 言
股票市场是国民经济的一个重要组成部分,随着经济的高速发展,股票市场也涌入越来越多的投资者。股票的价格波动受到多方面因素的影响,因此股票投资是一项高风险但同时高回报的项目。作为投资者来说,希望对股票价格有正确的预测从而达到降低风险获得收益的目的。长期以来,股票预测一直是一项具有吸引力的任务,但由于市场的随机性和参与者行为模式的波动性,股票预测仍然具有挑战性。
股票价格预测的研究可以分为统计学和非统计学两个方向。基于统计学的股票价格预测方法有传统的广义自回归条件异方差模型(Generalized AutoRegressive Conditional Heteroskedasticity, GARCH)[1],差分整合移动平均自回归模型(Autoregressive Integrated Moving Average model, ARIMA)[2]等,这些方法能很好的捕捉到股票价格的线性相关特征,但是对于非线性特征无法很好的处理。基于非统计学的股票价格预测方法可以分为两支,传统的机器学习方法和随后发展起来的深度学习方法。随着机器学习的兴起,支持向量机(Support Vector Machine, SVM)[3]不仅可以用作分类,也可以进行回归预测,陈懿冰[4]等人利用支持向量机模型对市场指数进行预测,发现在股市平稳性比较好的情况下预测结果比较好,但是突变情况下拟合不是很好,经过改进的决策树预测模型[5]可以提取股票序列特征进行回归预测,改进过后的BP神经也可以用来预测股价[6]。随着深度学习在各个领域中的发展和应用,越来越多的学者开始尝试利用深度学习进行股价预测。卷积神经网络(Convolutional Neural Network, CNN)在图像分类回归问题中得到广泛使用,Ashwin Siripurapu [7]将时序数据画成折线图来满足CNN卷积的特征提取,但是没有得到很好的结果;齐晓娜等[8]利用长短期记忆网络(Long Short-Term Memory, LSTM)进行股票价格预测可以获得比较优异的预测精度;刘震等[9]利用改进的基于循环神经网络(Recurrent Neural Network, RNN)的模型LSTM可以实现对股票价格的预测;Transformer最初提出是为了机器翻译问题[10],随后也被广泛应用于图像处理等领域,张倩玉等人[11]利用注意力机制捕获输入特征参数的权重并结合门控循环神经网络(Gated Recurrent Neural Network, GRU)进行股票价格预测;陈诗乐等人[12]提出了基于GA-Transformer模型的多因子股票预测方法,该方法使用遗传算法(Genetic Algorithm, GA)进行特征选择,并结合Transformer模型进行股票预测;也有学者融合情感特征如股票评论数据等自然语言来对股票价格进行预测[13]。
为了基于股票多因子历史数据对未来5日的股票收盘价格进行预测,我们设计了一种基于深度学习的集成预测算法。这一算法将改进的Transformer编码器模型、长短期记忆网络和时间卷积网络3种模型分别在单任务预测和多任务预测模式下训练,为不同模型的单任务预测和多任务预测集成设计了一种新的权重分配方式。利用本文提出的算法,可以基于当下股票的历史多因子数据对未来多日股票收盘价进行预测,为投资者股票操作提供参考。
1" "数据处理
1.1" 数据来源
本文采用的数据集来自IBM、洛斯保险、建设银行和上证指数,股票数据通过招商证券客户端下载得到。
1.2" 特征选择
股票市场中被广泛使用的是K线图,K线图数据包含股票的开盘价、收盘价、最高价和最低价,每日的K线图放在一起就是日K线图,日K线图能反映大势的状况和价格信息;在各股票数据平台上我们能观察到在股票不同的趋势位置,有与K线图对应的成交量,很多交易信号需要K线图结合成交量来判断。这个5个特征信息是股票市场交易的重要依据,所以本文选取股票的开盘价、收盘价、最高价、最低价和成交量作为特征来源。
1.3" "数据归一化
由于数据的量纲不同,我们对数据进行归一化处理。本文采用了最小最大归一化方法,根据式(1)将数据归一化。我们按8:1:1的比例去划分全部数据集,划分出训练数据、验证数据和测试数据。公平起见,在选择最大值最小值时只从训练数据中选择,即Di = {第i个因子的训练数据},对五个因子分别取最大值和最小值,然后在因子内进行归一化:
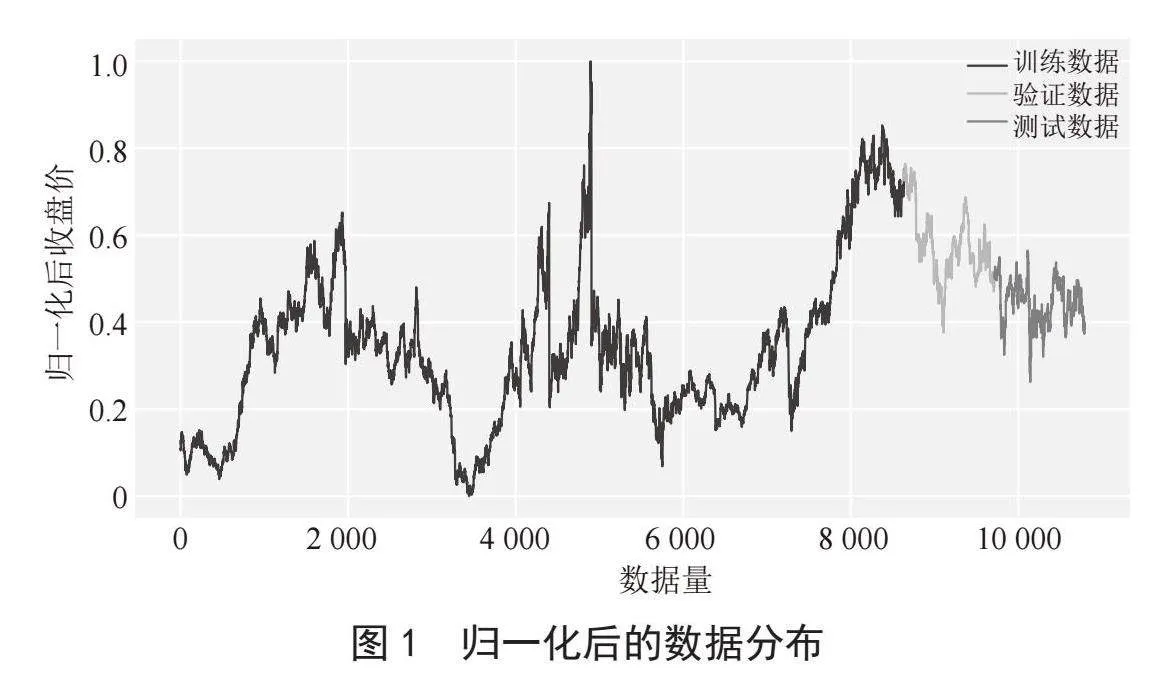
其中:i ∈ {1,2,3,4,5},k表示遍历全部数据。归一化后的数据如图1所示。
1.4" "数据集划分
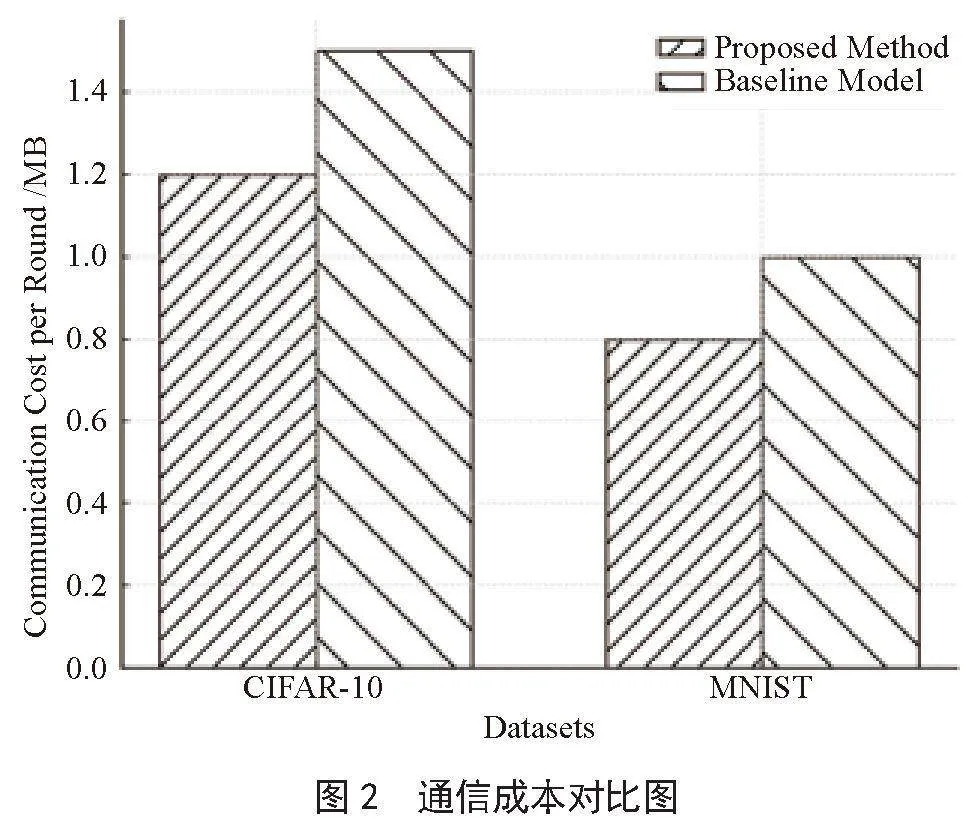
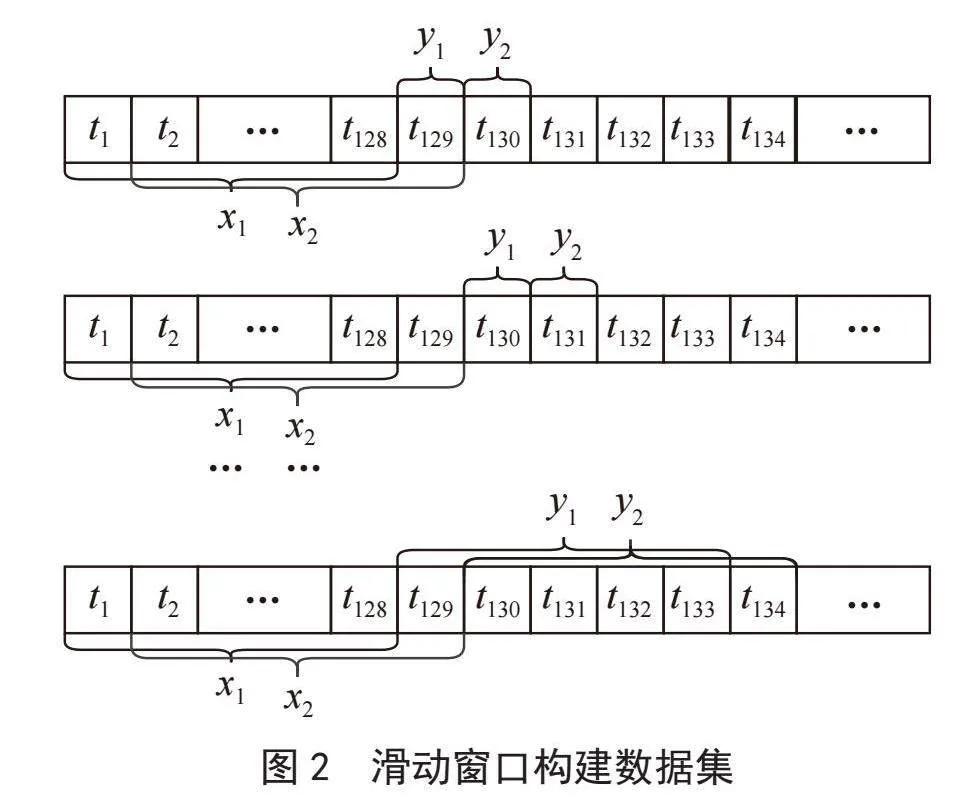
通过滑动窗口构建数据集样本,分别在划分好的训练数据、验证数据和测试数据中按图2方法构建训练集、验证集和测试集。验证集用来保存最优模型,测试集用来预测,下文呈现的实验结果均来自测试集。根据历史m天的数据预测未来n天。本文实验中m取128,在单任务回归预测中n取1,在多任务回归预测中n取5。
2" 网络结构
根据股票的历史数据来预测该股票未来的收盘价格属于回归问题,近年来,深度学习用来处理时间序列的常见模型有RNN、LSTM、TCN等,RNN网络可以利用历史数据对未来数据做出预测,但是学习不到长期依赖,而LSTM在RNN基础上做了改进,所以以下实验我们采用LSTM和TCN。Transformer最初用来处理机器翻译问题,随后在图片处理上也有很好的应用,其关键组件注意力机制也被很多模型添加引用。去除词嵌入组件以及对输出进行通道缩减和添加线性层后,Transformer编码层可以应用于回归问题。
2.1" Transformer编码层
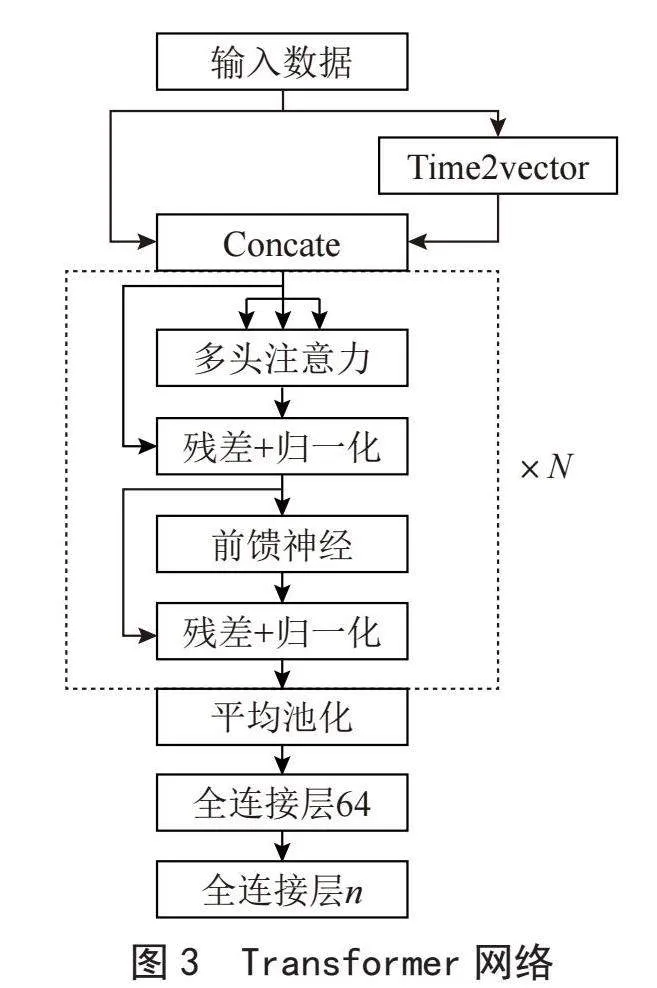
以Transformer编码层为主体结构,搭建了如图3所示的深度神经网络。不论是传统的自然语言理解还是本文研究的时间序列,都需要考虑前后顺序位置关系,用于自然语言处理的Transformer是将位置编码加到词向量中,而本文通过添加时间特征向量来体现时间信息[14]。
利用式(2)构造时间特征,选择k = 1,即非周期构造一个维度,周期性构造一个维度。x是原始时间序列特征,sin是周期性激活函数,w和b是可学习的参数。在实验中,sin函数使得算法能够捕获数据中的周期性行为,与此同时线性项(i = 0对应的公式)表示时间的非周期进程,用于捕获输入中的非周期性模式。
网络的输入是128×5的五因子历史股票数据,经过Time2vector层加上时间信息后变为128×7的历史数据,依次通过多头注意力层,残差和LayerNorm归一化层,前馈神经网络层和残差和LayerNorm归一化层,最后经过全局平均池化降低通道数,再经过线性层和dropout层输出结果。
2.2" TCN时间卷积网络
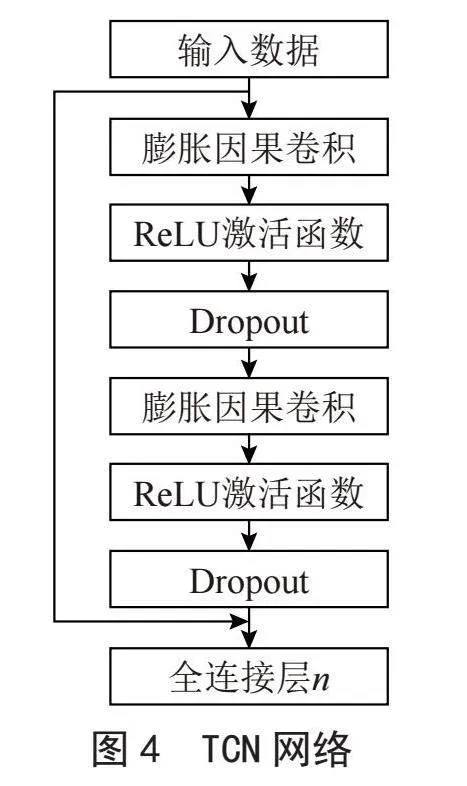
TCN模型是以CNN模型为基础,并做了因果卷积(Causal Convolution)、膨胀卷积(DilatedConvolution)和残差模块(Residual block)的改进。搭建如4图所示的TCN网络结构。输出序列经过一个全连接层后输出最终结果。
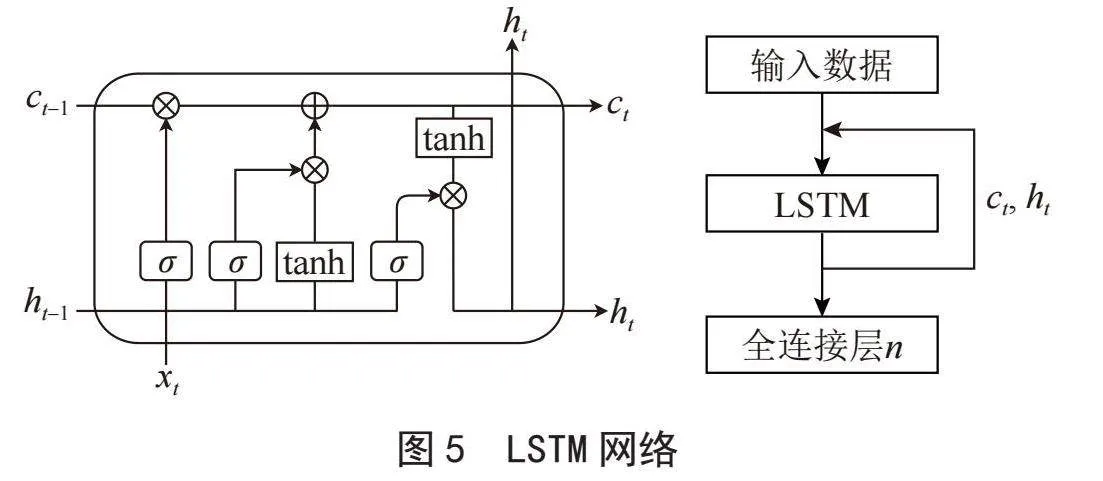
2.3" LSTM长短期记忆网络
LSTM是一种时间循环神经网络,它的提出是为了解决一般的RNN(循环神经网络)存在的长期依赖问题,数据经过LSTM后再添加一个全连接层输出最终结果。LSTM网络结构如图5所示。
2.4" 集成学习
集成学习是一种学习器结合的方法,最初用于分类问题,由训练数据构建一组基学习器,然后通过对每个基学习器的预测进行投票来产生最终预测。常见的集成方法有两种,同构集成和异构集成,本文采用的是异构集成,用不同类型的学习器,即我们前文提到的3种模型框架。
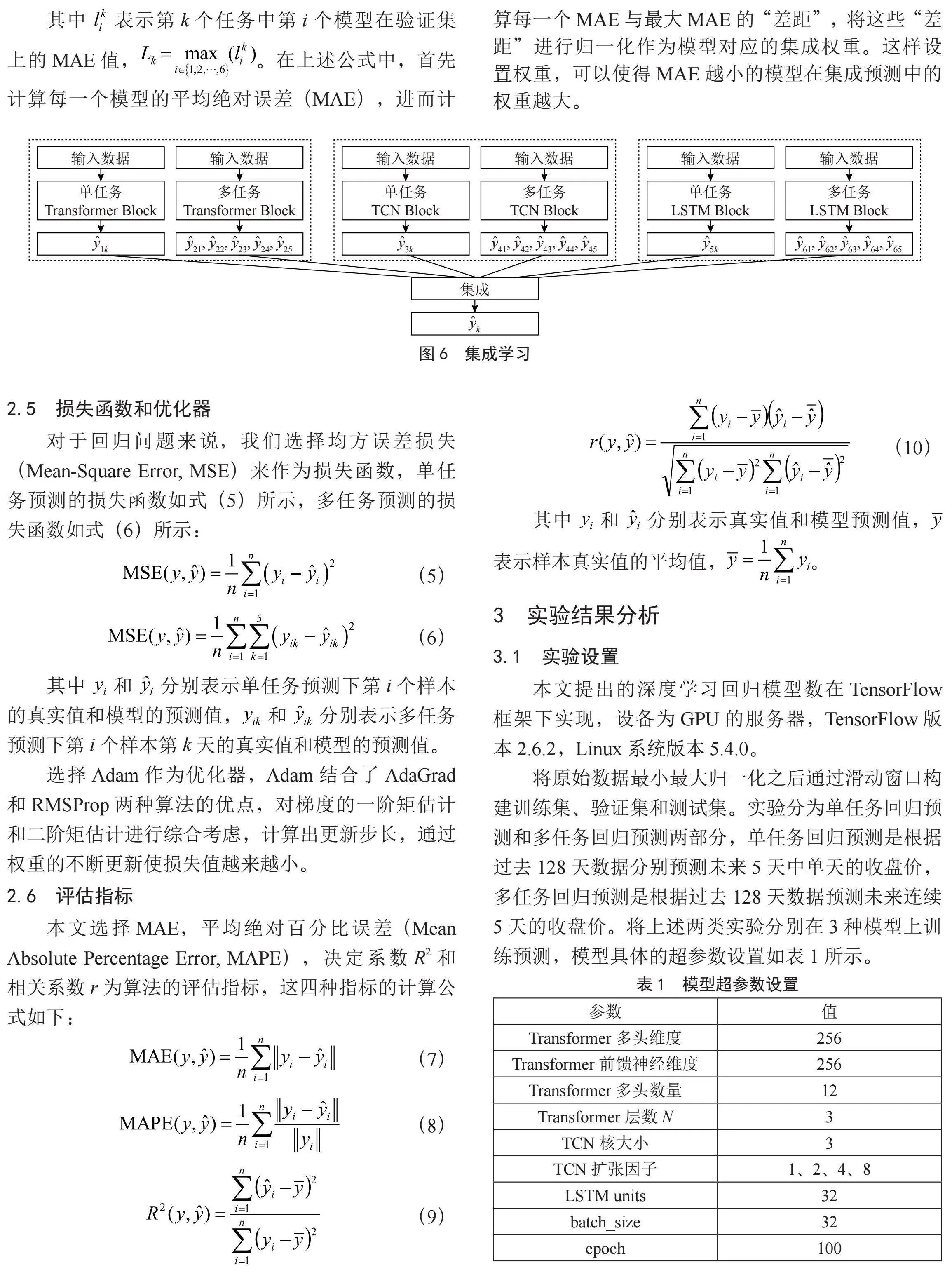
对回归问题来说,基于3种模型预测未来5天的股票收盘价,其中包括单任务回归预测和多任务回归预测,将单任务回归预测第k天的结果 ,i = 1,3,5以及多任务回归预测中第k天的结果 ,i = 2,4,6进行集成得到最终的预测结果,其中i为奇数表示3种模型单任务预测,i为偶数表示3种模型多任务预测,i = 1,2表示Transformer Block;i = 3,4表示TCN Block;i = 5,6表示LSTM Block。预测第k天的整体流程图如图6所示,其中k = 1,2,3,4,5。集成的计算公式如下:
其中" 表示集成的权重,在平均集成下,=1/6。
在经典的集成预测中,每一个基本预测模型在最终的预测中占有完全相等的投票权。一个自然的想法是,动态的为所有预测模型设置集成权重,使得预测精度更高的预测模型获得更大的集成权重,从而提升集成预测的准确性。这里,我们利用平均绝对误差(Mean Absolute Error, MAE)来刻画预测模型的准确性,MAE越小的模型被赋予越大的集成权重。集成权重的具体计算方式为:
其中" 表示第k个任务中第i个模型在验证集上的MAE值,。在上述公式中,首先计算每一个模型的平均绝对误差(MAE),进而计算每一个MAE与最大MAE的“差距”,将这些“差距”进行归一化作为模型对应的集成权重。这样设置权重,可以使得MAE越小的模型在集成预测中的权重越大。
2.5" 损失函数和优化器
对于回归问题来说,我们选择均方误差损失(Mean-Square Error, MSE)来作为损失函数,单任务预测的损失函数如式(5)所示,多任务预测的损失函数如式(6)所示:
其中" 和" 分别表示单任务预测下第i个样本的真实值和模型的预测值, 和" 分别表示多任务预测下第i个样本第k天的真实值和模型的预测值。
选择Adam作为优化器,Adam结合了AdaGrad和RMSProp两种算法的优点,对梯度的一阶矩估计和二阶矩估计进行综合考虑,计算出更新步长,通过权重的不断更新使损失值越来越小。
2.6" 评估指标
本文选择MAE,平均绝对百分比误差(Mean Absolute Percentage Error, MAPE),决定系数R2和相关系数r为算法的评估指标,这四种指标的计算公式如下:
其中" 和" 分别表示真实值和模型预测值, 表示样本真实值的平均值,。
3" 实验结果分析
3.1" 实验设置
本文提出的深度学习回归模型数在TensorFlow框架下实现,设备为GPU的服务器,TensorFlow版本2.6.2,Linux系统版本5.4.0。
将原始数据最小最大归一化之后通过滑动窗口构建训练集、验证集和测试集。实验分为单任务回归预测和多任务回归预测两部分,单任务回归预测是根据过去128天数据分别预测未来5天中单天的收盘价,多任务回归预测是根据过去128天数据预测未来连续5天的收盘价。将上述两类实验分别在3种模型上训练预测,模型具体的超参数设置如表1所示。
3.2" 结果分析
将模型在测试集上进行预测,由于初始数据进行了归一化,下面的结果都是返回归一化之前即原始价格去计算损失。模型名称后缀O表示单任务回归预测,C表示多任务回归预测,平均集成表示权重取1/6的单任务回归预测和多任务回归预测集成,本文集成表示按本文方法重新分配权重的单任务回归预测和多任务回归预测集成。
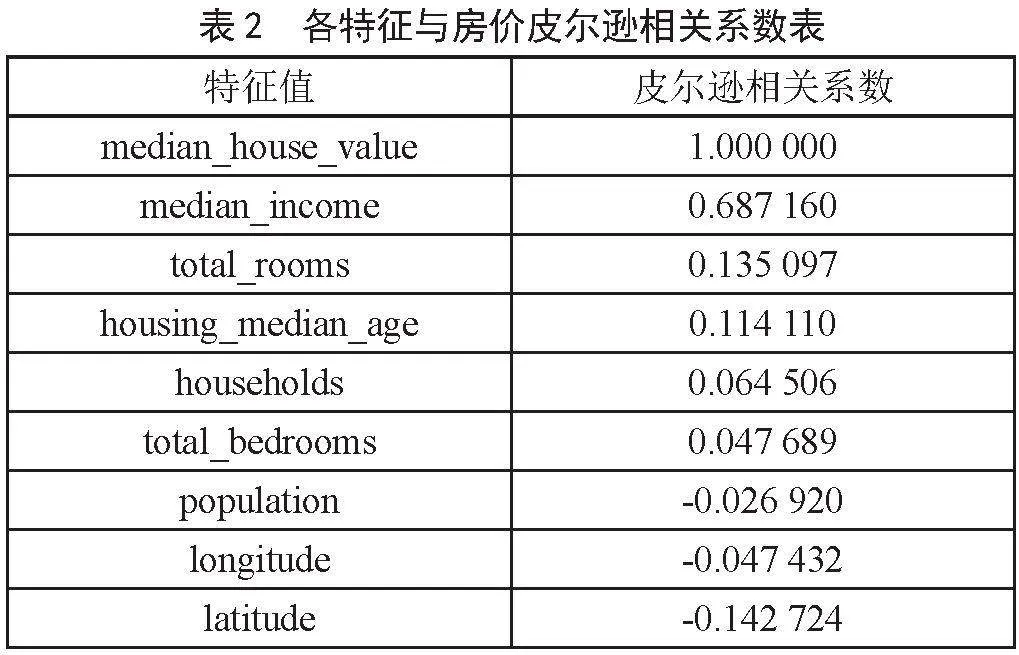
表2是预测未来5天股票价格在4个数据集上的MAE结果,可以看出本文设计的权重分配方式相比平均集成在4个数据集上MAE都减小,并且本文集成相比6种基本模型的MAE值都达到了最优,说明本文方法的有效性。在和SVR [4]模型的比较中本文集成的MAE值更优。和ARIMA [2]模型的比较中3个数据集上最优,剩余1个数据集上次优。
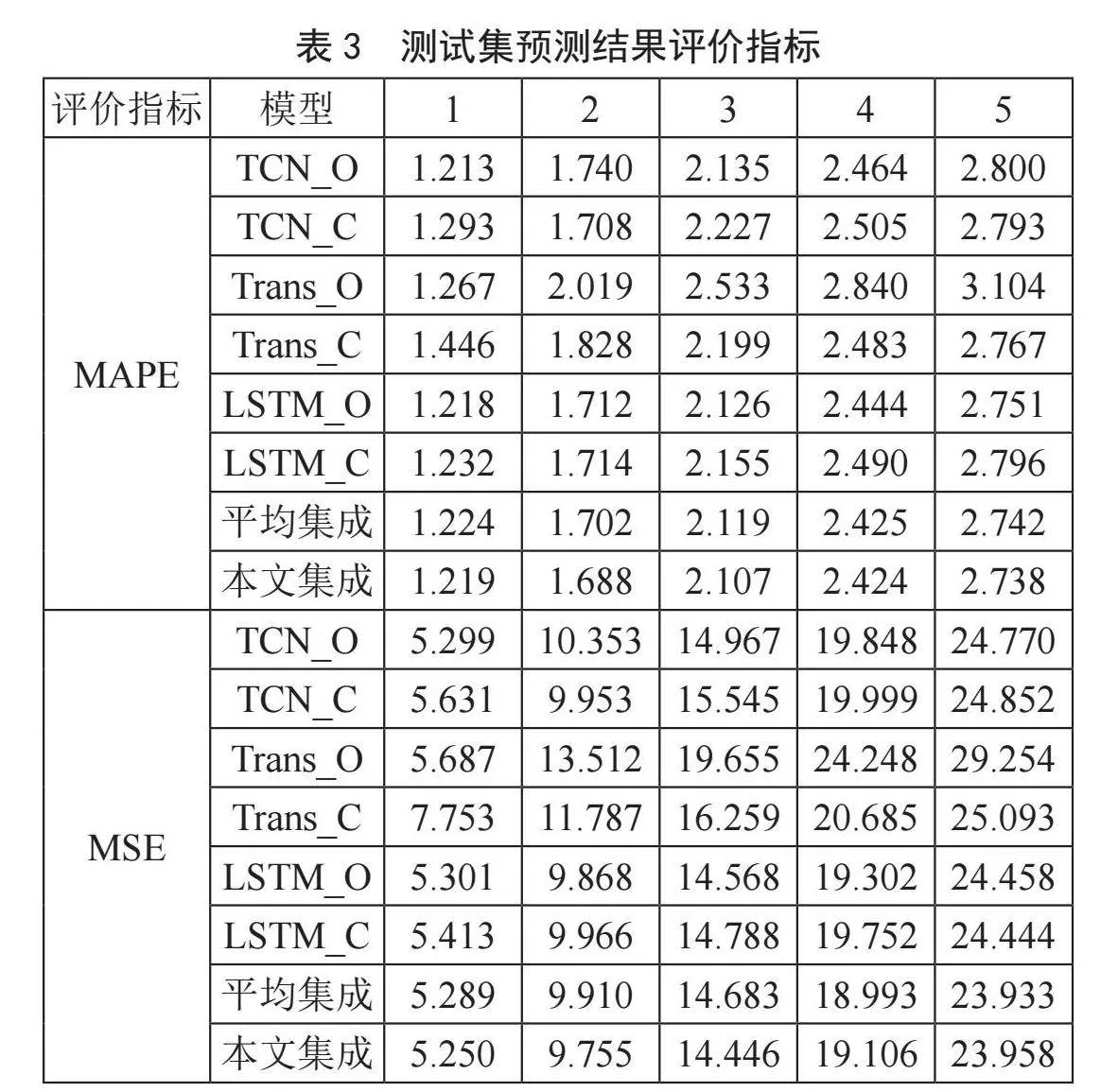
表2的结果显示在5天的总任务上本文集成都达到最优,下面对IBM数据集结果在单天维度上进行详细分析。表3分别展示了IBM测试集在不同模型以及单天维度上的结果。从表3中可以看出,单任务回归预测和多任务回归预测在不同的模型上都各有优势,对于TCN和LSTM来说,单任务和多任务的结果差距不是很明显,但是对于Transformer来说,单任务预测未来第1天的结果优势明显,但是随着预测时间的向后推移,Transformer多任务的优势体现出来;整体来看,无论是单任务预测还是多任务预测,预测未来的时间越远,误差越大。
在单天维度上,应用本文提出的权重分配方式后预测精度相比于平均集成都有明显提高,说明该种权重分配方式的有效性;在原先6种模型上,第1天优势在TCN_O,第2天优势在TCN_C,第3天优势在LSTM_O,最优值分散于不同的模型上,经过分配权重的集成后,在单天维度上指标的优势变得集中,单天维度的最优值不再分散于各个模型上,这也是集成方法的优势所在。
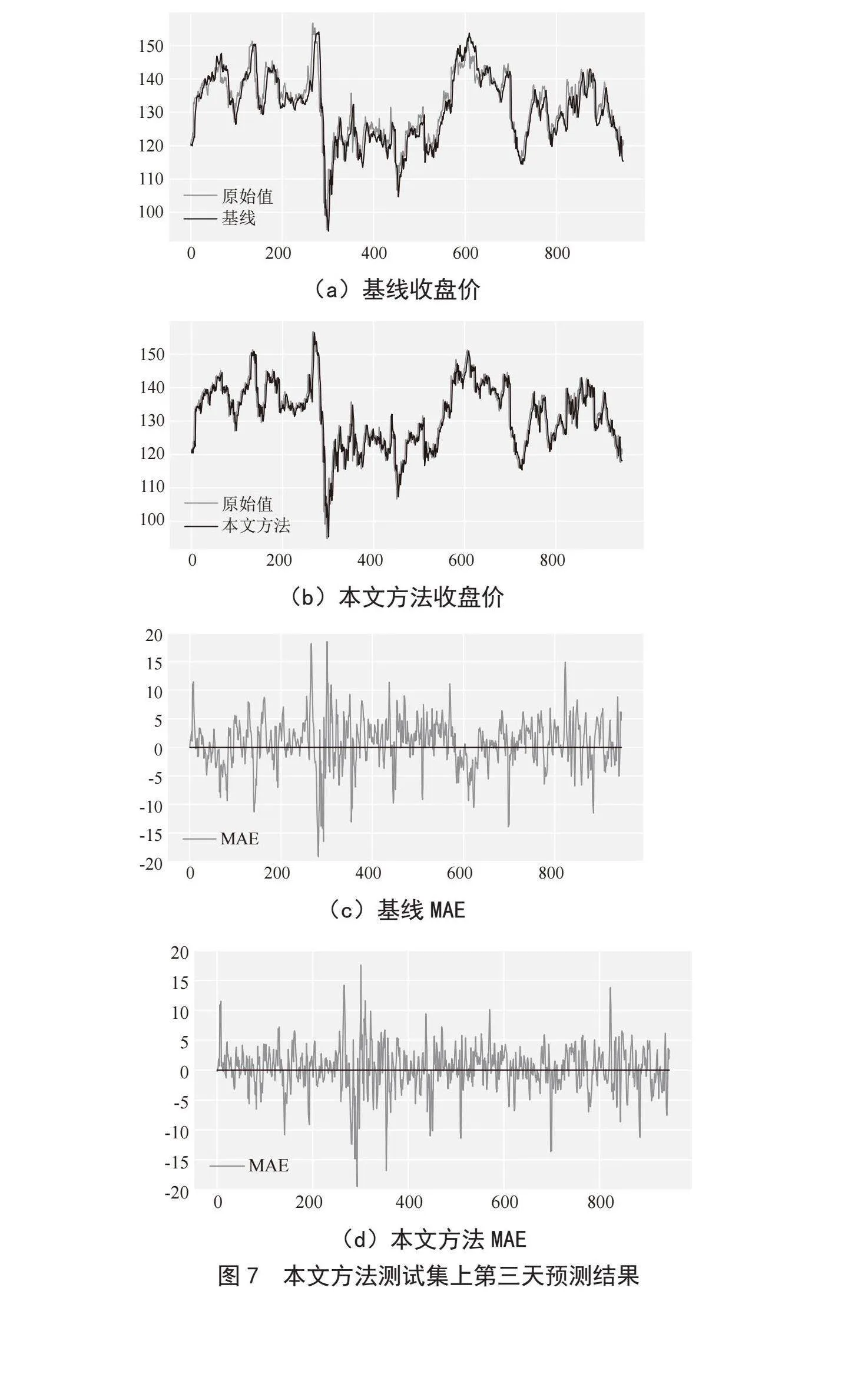
将单任务预测和多任务预测的6种模型按本文方法分配权重集成在测试集上第3天的预测结果以及MAE画图,基线模型选取的是Transformer Block单任务预测在测试集第3天上的结果。从图7中可以看出本文方法数据拟合的比较好,MAE波动更小且靠近0。
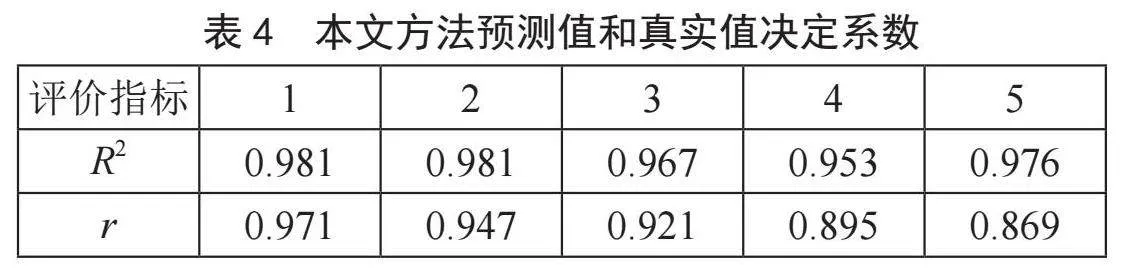
为了展示本文方法在股票价格的预测值和真实值的分布,计算决定系数和相关系数如表4所示,通过结果可以看出两者存在强相关性,同时随着时间的向后推移,相关系数变小,这也和前文提到的预测未来的时间越远MAE误差越大相符合。
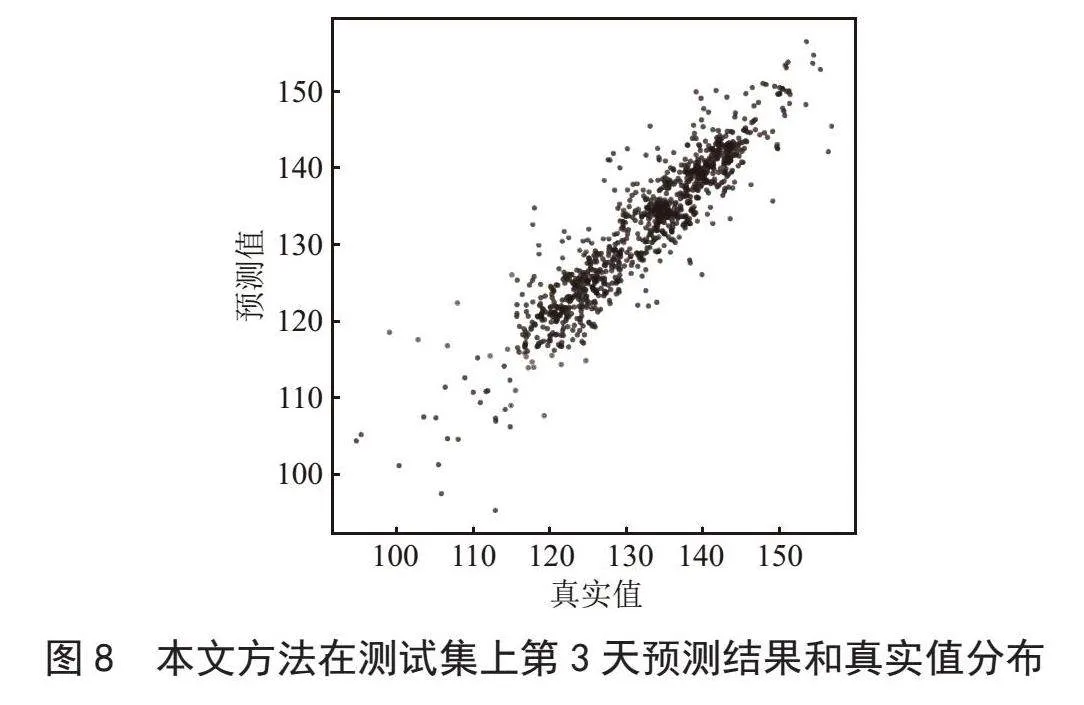
将股票价格的真实值作为横轴,本文方法的预测值作为纵轴,绘制第3天的散点图如图8所示,可以更直观地看出两者的相关性。
4" 结" 论
本文基于股票的历史开盘价、收盘价、最高价、最低价和交易量数据,提出了预测未来多日股票收盘价的集成算法。这一算法将改进的Transformer编码器模型、长短期记忆网络和时间卷积网络3种模型分别在单任务预测和多任务预测模式下训练,并且我们为不同模型的单任务预测和多任务预测集成设计了一种新的权重分配方式。在测试集上的结果表明本文方法有较低的平均绝对误差和较高的相关性。通过本文方法投资者可以作为参考来预测未来股价进行股票投资。未来的研究考虑纳入更多的因子作为特征,并且加入投资者情绪信息来辅助预测。
参考文献:
[1] BOLLERSLEV T. Generalized autoregressive conditional heteroskedasticity [J].Eeri Research Paper,1986,31(3):307-327.
[2] BOX G E P,PIERCE D A. Distribution of residual autocorrelations in autoregressive-integrated moving averagetime seriesmodels [J].Journal of the American statistical Association,1970,65(332):1509-1526.
[3] CORTES C,VAPNIK V. Support vector machine [J].Machine learning,1995,20(3):273-297.
[4] 陈懿冰,张玲玲,聂广礼,等.基于改进的支持向量回归机的金融时序预测 [J].数学的实践与认识,2012,42(4):38-44.
[5] 李想.基于XGBoost算法的多因子量化选股方案策划 [D].上海:上海师范大学,2017.
[6] ZHANG H. The forecasting model of stock price based on PCA and BP neural network [J].Journal of Financial Risk Management,2018,7(4):369-385.
[7] SIRIPURAPU A. Convolutional networks for stock trading [J].Stanford Univ. Dep. Comput. Sci,2014,1(2):1-6.
[8] 齐晓娜,张宇敬,郑艳娟,等.深度学习算法在股票价格预测方面的研究 [J].软件,2021,42(7):70-72.
[9] 刘震,王惠敏,华思瑜,等.基于深度学习的股价预测研究 [J].科技创新导报,2018,15(13):247-248.
[10] VASWANI A,SHAZEER N,PARMAR N,et al. Attention is all you need [C]//NIPS17: Proceedings of the 31st International Conference on Neural Information Processing Systems.Red Hook:Curran Associates Inc,2017:6000-6010.
[11] 张倩玉,严冬梅,韩佳彤.结合深度学习和分解算法的股票价格预测研究 [J].计算机工程与应用,2021,57(5):56-64.
[12] 陈诗乐,王笑,周昌军.基于GA-Transformer模型的多因子股票预测 [J].广州大学学报:自然科学版,2021,20(1):44-55.
[13] 严冬梅,何雯馨,陈智.融合情感特征的基于RoBERTa-TCN的股价预测研究 [J].数据分析与知识发现,2022,6(12):123-133.
[14] KAZEMI S M,GOEL R,EGHBALI S,et al. Time2vec:Learning a vector representation of time[J].arXiv:
1907.05321 [cs.LG].(2019-07-11).http://arxiv.org/abs/1907.05321.
作者简介:郭慧婷(1998—),女,汉族,山西晋中人,硕士在读,研究方向:深度学习在金融时间序列上的应用;常延贞(1981—),女,汉族,山东滨州人,副教授,博士,研究方向:偏微分方程数值解、计算最优控制;厉亮(1984—),男,汉族,台湾苗栗人,副教授,博士,研究方向:随机偏微分方程、金融数学、量化投资+AI;通讯作者:徐永利(1982—),男,汉族,山东济南人,教授,博士,研究方向:统计学习理论、机器学习、计算机辅助青光眼诊断。