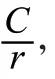
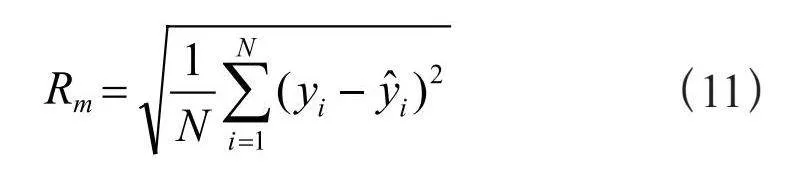
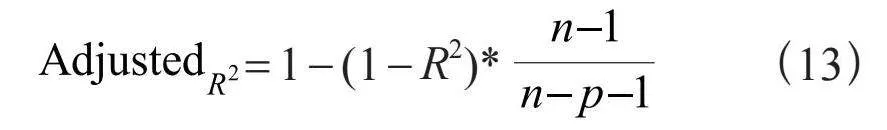
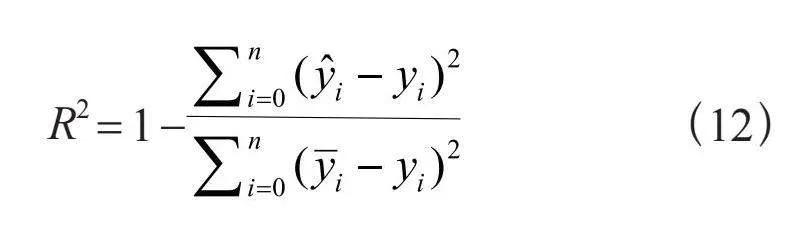
摘" 要:为提高自动扶梯轴承剩余使用寿命(RUL)预测模型的预测精度和泛化能力,提出一种基于卷积神经网络(CNN)的轴承RUL预测方法。首先基于3σ准则对原始数据进行去噪,通过快速傅里叶变换获得其频率特征,其次将不同于传统时间序列数据划分方法的分层抽样应用于数据划分,并构造一个由三个卷积层和两个全连通层组成的深度卷积神经网络DCNN模型,最后利用NASA IMS数据集对预处理方法、DCNN模型精度和泛化能力进行评估,证明了该方法的优越性。
关键词:剩余寿命预测;3σ准则;分层抽样;DCNN;泛化能力
中图分类号:TP391;TH133.3 文献标识码:A 文章编号:2096-4706(2024)10-0032-06
Prediction Method for Bearing Remaining Useful Life Based on
Convolutional Neural Networks
ZHANG Hao1, ZHAO Jun1, WANG Lu1, ZHANG Yinlong2, CHENG Siyu2
(1.Nanjing Metro Construction Co., Ltd., Nanjing" 211806, China;
2.China Railway Siyuan Survey and Design Group Co., Ltd., Wuhan" 430063, China)
Abstract: To improve the prediction accuracy and generalization ability of the Remaining Useful Life (RUL) prediction model for escalator bearings, a bearing RUL prediction method based on Convolutional Neural Network (CNN) is proposed. Firstly, it denoises the original data based on 3σ criterion, obtains its frequency characteristics through fast Fourier transformation. Secondly, it applies layered sampling different from traditional time series data partitioning methods to data partitioning, and constructs a Deep Convolutional Neural Network (DCNN) model consisting of three convolutional layers and two fully connected layers. Finally, the NASA IMS dataset is used to evaluate the preprocessing method, DCNN model accuracy, and generalization ability, proving the superiority of this method.
Keywords: RUL prediction; 3σ criterion; layered sampling; DCNN; generalization ability
0" 引" 言
自动扶梯轴承剩余使用寿命(Remain Useful Life, RUL)预测对公共安全极其重要,精确的RUL预测可以减少自动扶梯的维修停梯时间,提高运营效益并降低运营成本[1-3],确保采取适当的维护决策[4],避免扶梯设备造成的人员伤亡和财产损失[5],研究和提高自动扶梯轴承RUL预测技术的准确性具有较强的现实意义[6-8]。
深度学习结合不同的神经网络可以在RUL预测中取得优异的结果,泛化能力是评价模型预测性能的重要指标[9]。基于此,本文提出了一种用于轴承RUL预测的方法,利用3σ准则去除原始数据中的粗监测误差,通过快速傅里叶变换从时域数据中获得轴承的频率特征,基于时间和频率特征通过分层抽样构建训练集和测试集。如果训练后损失函数最小,则保存训练后的模型。如果损失函数不是最小的,则采用反向传播法来调整卷积层和全连接层的权重W和偏置B,直到损失函数达到最小。最后使用测试数据对训练好的模型进行测试。如果指数值是最佳的,则获得预测的RUL。如果指数值不是最优的,则调整训练次数、核大小和隐藏层深度,以获得最优的指数值。
1" 数据预处理
1.1" 数据去噪
假设数据服从高斯分布,采用3σ准则来消除测量数据中的粗差,数据分布几乎完全集中在(μ-3σ,μ+3σ)区间,超过该区间的数据比例为0.27%,区间之外的数据在此步骤被去除。
1.2" 时间和频率特征选择
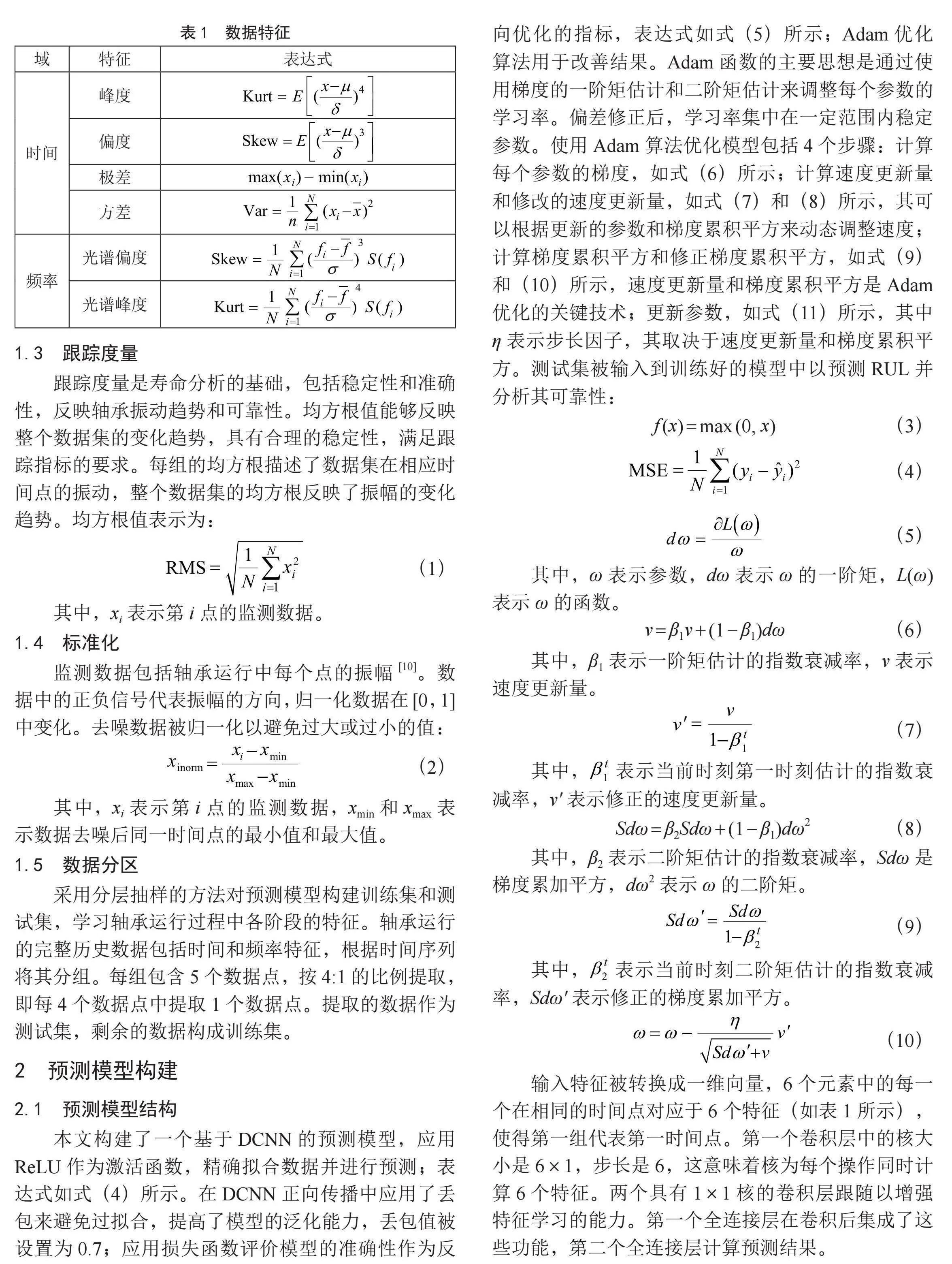
通过快速傅里叶变换从原始时域获取频率特征,如表1所示。
1.3" 跟踪度量
跟踪度量是寿命分析的基础,包括稳定性和准确性,反映轴承振动趋势和可靠性。均方根值能够反映整个数据集的变化趋势,具有合理的稳定性,满足跟踪指标的要求。每组的均方根描述了数据集在相应时间点的振动,整个数据集的均方根反映了振幅的变化趋势。均方根值表示为:
其中,xi表示第i点的监测数据。
1.4" 标准化
监测数据包括轴承运行中每个点的振幅[10]。数据中的正负信号代表振幅的方向,归一化数据在[0,1]中变化。去噪数据被归一化以避免过大或过小的值:
其中,xi表示第i点的监测数据,xmin和xmax表示数据去噪后同一时间点的最小值和最大值。
1.5" 数据分区
采用分层抽样的方法对预测模型构建训练集和测试集,学习轴承运行过程中各阶段的特征。轴承运行的完整历史数据包括时间和频率特征,根据时间序列将其分组。每组包含5个数据点,按4:1的比例提取,即每4个数据点中提取1个数据点。提取的数据作为测试集,剩余的数据构成训练集。
2" 预测模型构建
2.1" 预测模型结构
本文构建了一个基于DCNN的预测模型,应用ReLU作为激活函数,精确拟合数据并进行预测;表达式如式(4)所示。在DCNN正向传播中应用了丢包来避免过拟合,提高了模型的泛化能力,丢包值被设置为0.7;应用损失函数评价模型的准确性作为反向优化的指标,表达式如式(5)所示;Adam优化算法用于改善结果。Adam函数的主要思想是通过使用梯度的一阶矩估计和二阶矩估计来调整每个参数的学习率。偏差修正后,学习率集中在一定范围内稳定参数。使用Adam算法优化模型包括4个步骤:计算每个参数的梯度,如式(6)所示;计算速度更新量和修改的速度更新量,如式(7)和(8)所示,其可以根据更新的参数和梯度累积平方来动态调整速度;计算梯度累积平方和修正梯度累积平方,如式(9)和(10)所示,速度更新量和梯度累积平方是Adam优化的关键技术;更新参数,如式(11)所示,其中η表示步长因子,其取决于速度更新量和梯度累积平方。测试集被输入到训练好的模型中以预测RUL并分析其可靠性:
其中,ω表示参数,dω表示ω的一阶矩,L(ω)表示ω的函数。
v = β1v + (1 - β1)dω" " " " " " " " " " "(6)
其中,β1表示一阶矩估计的指数衰减率,v表示速度更新量。
其中, 表示当前时刻第一时刻估计的指数衰减率,v表示修正的速度更新量。
Sdω = β2Sdω + (1 - β1)dω2" " " " " " " " " " " " " "(8)
其中,β2表示二阶矩估计的指数衰减率,Sdω是梯度累加平方,dω2表示ω的二阶矩。
其中, 表示当前时刻二阶矩估计的指数衰减率,Sdω表示修正的梯度累加平方。
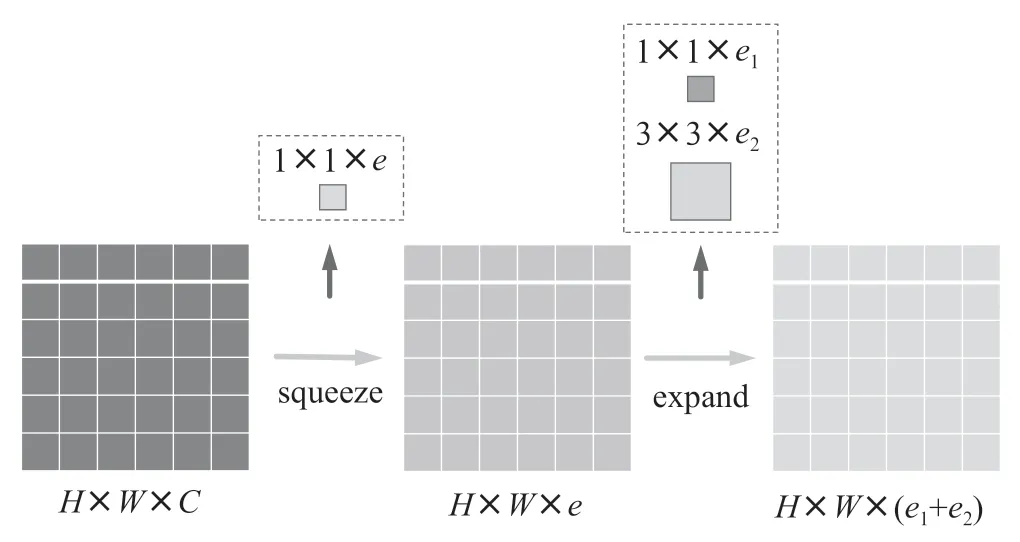
输入特征被转换成一维向量,6个元素中的每一个在相同的时间点对应于6个特征(如表1所示),使得第一组代表第一时间点。第一个卷积层中的核大小是6×1,步长是6,这意味着核为每个操作同时计算6个特征。两个具有1×1核的卷积层跟随以增强特征学习的能力。第一个全连接层在卷积后集成了这些功能,第二个全连接层计算预测结果。
2.2" 模型评估
该模型由均方根误差(Rm)、拟合优度(R2)、调整后的拟合优度(调整后的R2)进行评估。
Rm表示一个衡量预测值和实际值之间差异的指数。Rm越接近0,预测结果越准确,计算式为:
其中,yi表示实际值, 表示预测值。
R2表示统计学中用于评估回归模型拟合度的优秀标准。R2值通常在[0,1]范围内变化。值越接近1,模型的拟合越好。当模型拟合不好时,函数值接近于0。计算式为:
其中, 表示平均值,n表示数据中的样本数。
根据式(12),当样本数量相对较大时,R2增加,因此拟合优度可能不能准确地表示评估模型的性能,尤其是在大样本量的情况下。为了克服这个问题,提出了一种调整的" 来避免数据样本数量对模型评价的影响。计算式为:
其中,n表示数据中的样本数量,p表示数据中的特征数量。
3" 实验分析
本文利用NASA IMS数据集中的3个轴承运行的监测信息来进行模型验证。每个轴承都配有一个传感器,每次记录20 480个点的振动。
3.1" 模型比较
选择RNN、LSTM作为比较模型。为了使比较更有说服力和有效性,选择每个模型的最优预测结果进行比较;因此,每个模型数据集的划分比例是不同的:
1)RNN。为了保证比较的公平性,基于TensorFlow框架构建了RNN预测模型。将数据以8:2的比例分成训练集和测试集,并构建4个RNN层。最后一层是全连接层。采用ReLU作为激活函数,均方误差作为损失函数,采用Adam优化算法。每层神经元分别为33、17、6、1,丢包值设置为0.7。
2)LSTM。基于TensorFlow框架,构造了一个具有三个隐藏层的LSTM预测模型。数据集按照7:3的比例分为训练集和测试集。最后一层应用ReLU作为激活函数。损失函数采用均方误差,采用Adam优化算法。LSTM由四层组成;每层神经元分别为35、24、11和1,丢包值设置为0.7。
3)DCNN。对于本文提出DCNN模型,数据集按照4:1的比例分为训练集和测试集。
3.2" 模型验证
选择第二组IMS数据集中轴承1的监测数据作为模型训练数据。通过两个实验验证了该方法的有效性。实验一评估了本文提出数据去噪方法的有效性,实验二评估了模型的泛化能力。
3.2.1" 实验一
对于第1个轴承的运行数据,使用不同的数据预处理方法(无去噪、硬阈值去噪、软阈值去噪和3σ准则去噪)比较3个模型(RNN、LSTM、DCNN)的预测,以确定去噪方法对预测精度的影响:
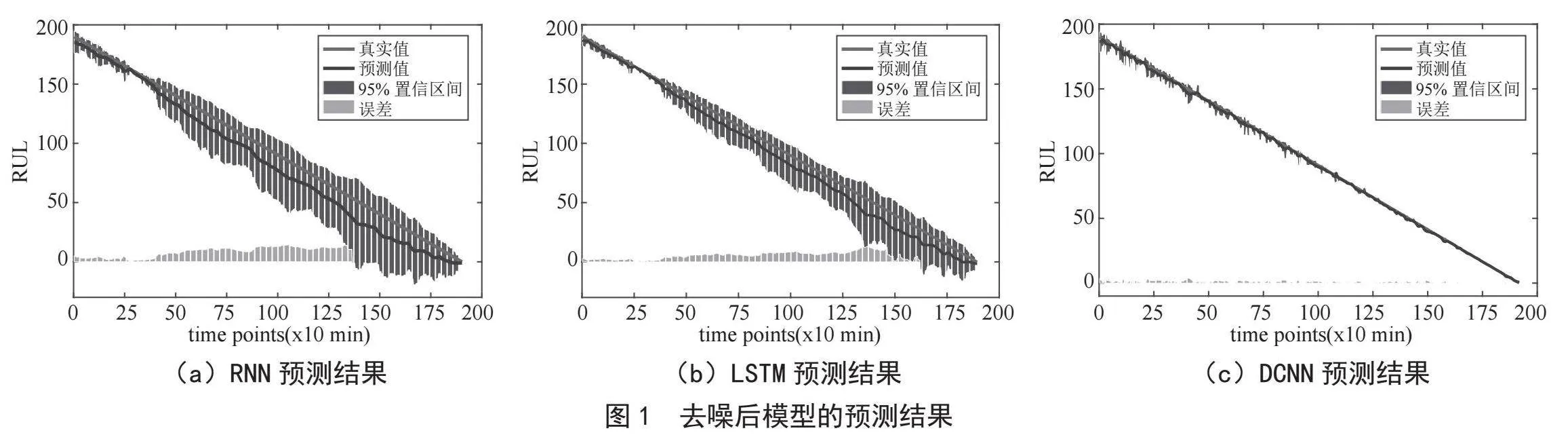
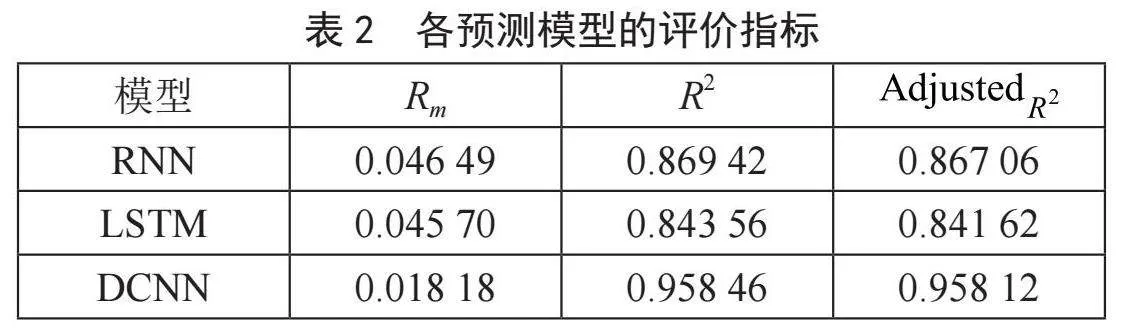
1)没有去噪的数据。实验结果如图1所示,RNN和LSTM模型的预测曲线与真实曲线有很大的不同,就95%置信区间和预测误差而言,最小波动出现在DCNN中,各模型的评价指标如表2所示。
表2中的定量分析表明,各评价指标的最优值为Rm = 0.018 18,R2 = 0.958 46,调整后的R2 = 0.958 12,均由DCNN模型实现。综合定性和定量分析表明,当数据未去噪时,DCNN模型的预测值最接近真实值。
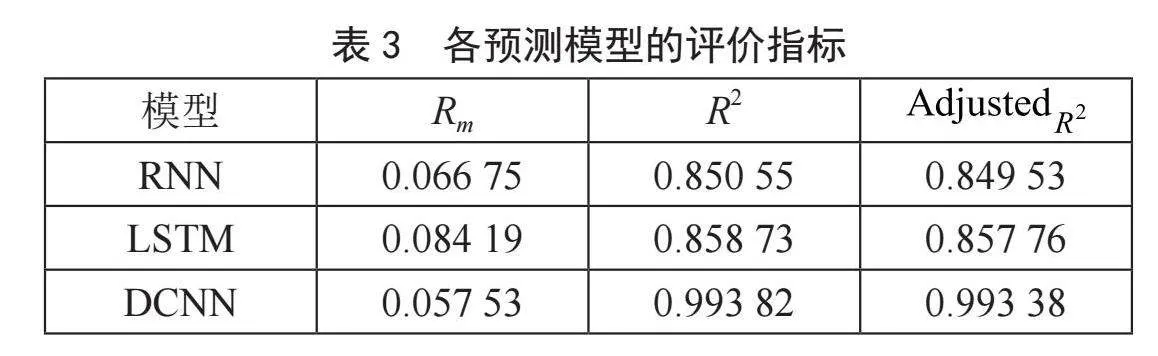
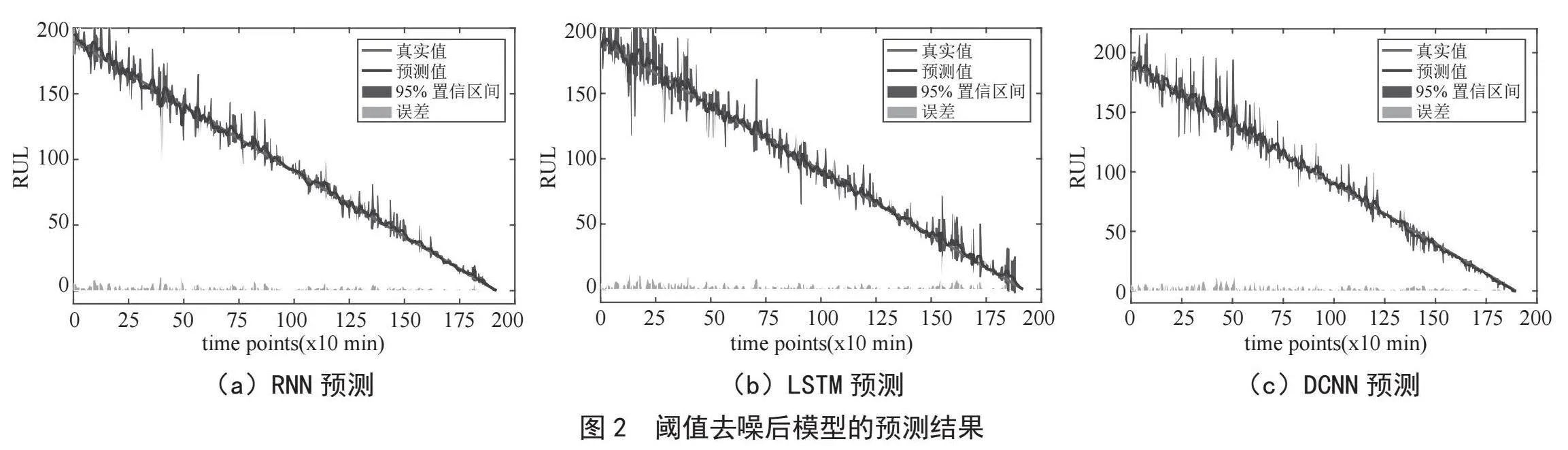
2)硬阈值去噪。硬阈值去噪在提高精度方面是有效的,结果如图2所示,评价指标如表3所示。
表3中的定量分析表明,除了得分指标之外,DCNN可以实现每个评估指标的最佳值,因为得分函数对高估给出了较大的惩罚,对预测不足给出了较小的惩罚。最优值为Rm = 0.057 53,R2 = 0.993 82,调整后的R2 = 0.993 38。
综合分析表明,DCNN可以在硬阈值去噪的情况下获得理想的预测结果,连续卷积操作有助于提高模型的预测能力。
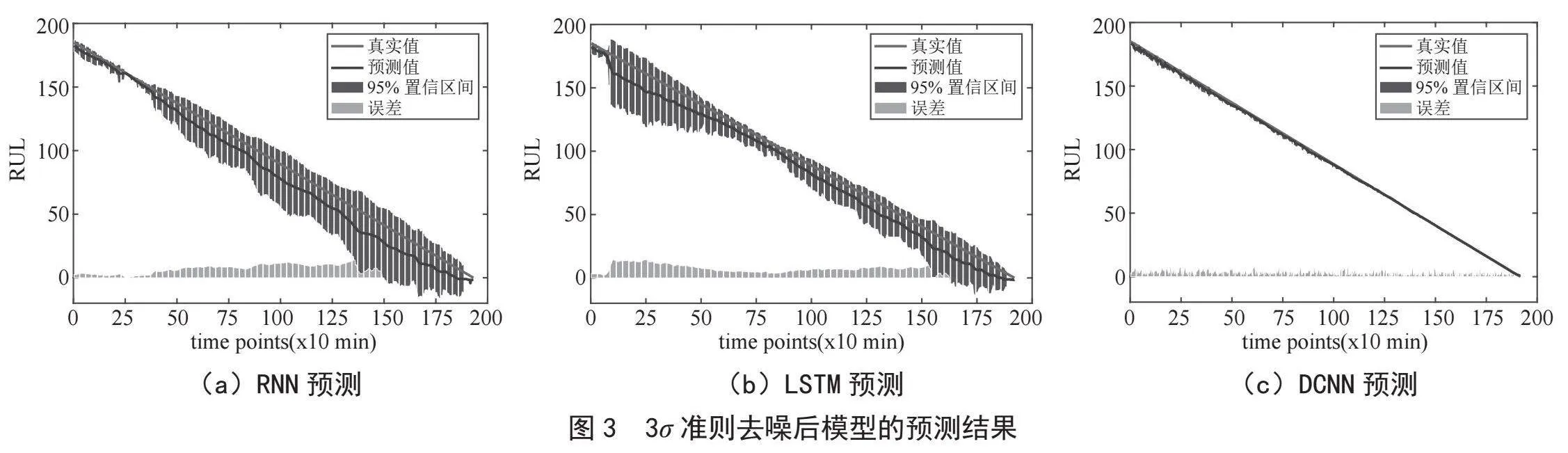
3)3σ准则去噪。本文提出的3σ准则去噪后模型的结果如图3所示,评价指标如表4所示。
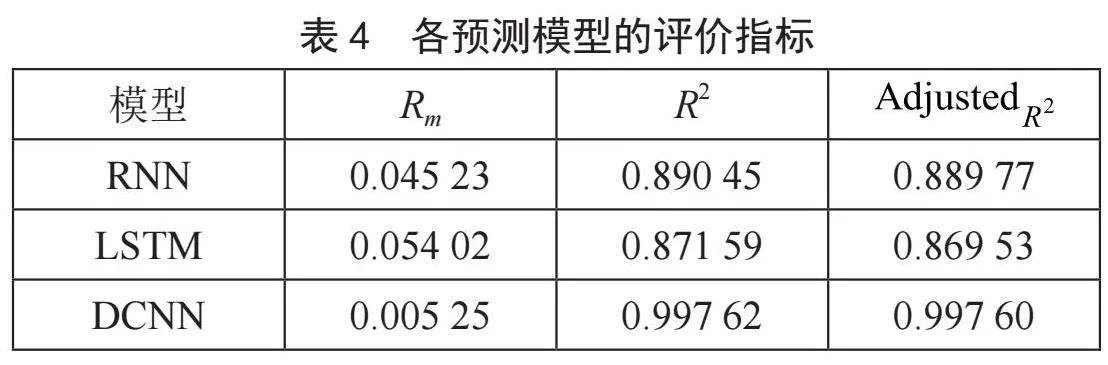
表5中的定量分析表明,各评价指标的最优值为Rm = 0.005 25,R2 = 0.997 62,调整后的R2 = 0.997 60,均由DCNN模型实现。
根据对三者的定量分析,用3σ准则去噪,预测值与实际值最接近。综合比较后可知采用3σ准则去噪结合DCNN可以得到最佳的预测结果。
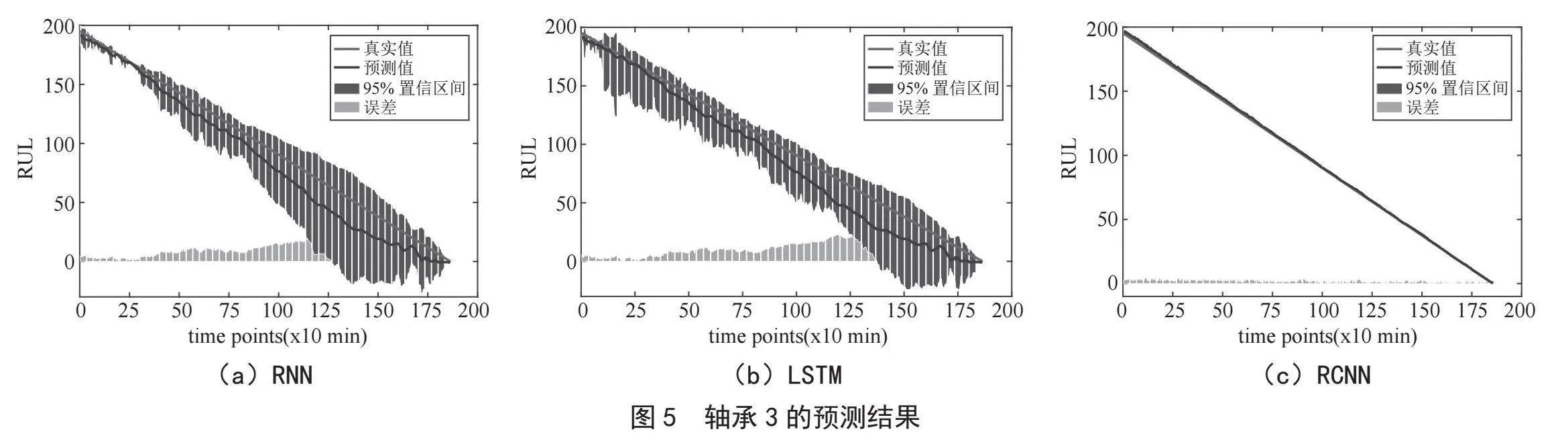
3.2.2" 实验二
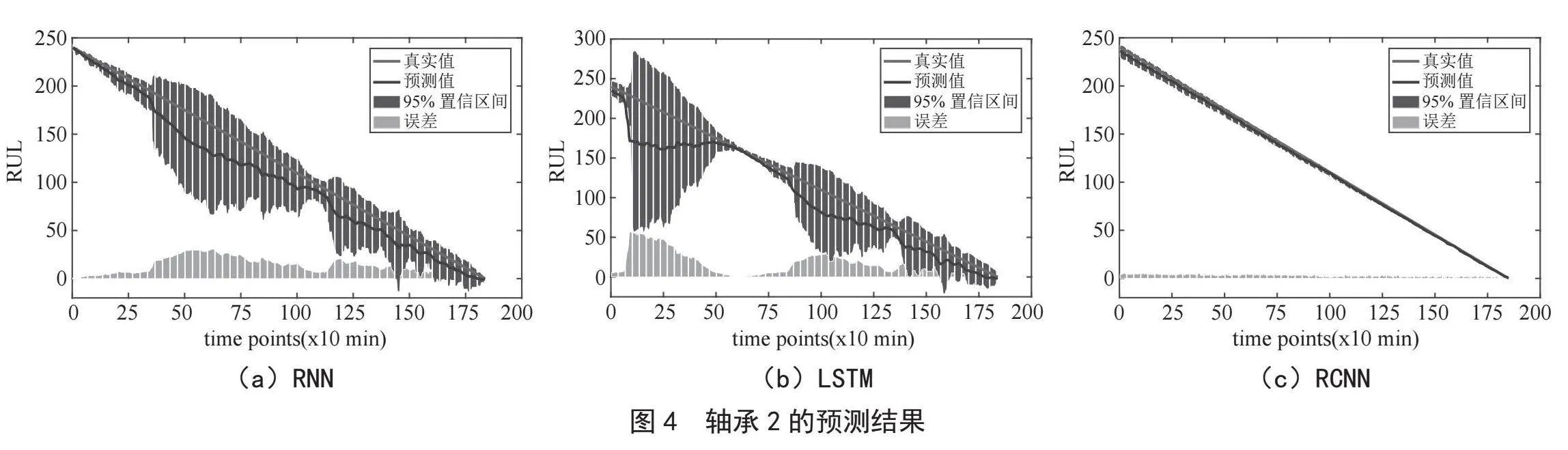
由于各轴承的退化趋势不同,选择第2、3轴承的运行数据作为实验测试数据,以验证模型的泛化能力,并评估模型依赖于每个数据集的性能。实验一结果如图4、图5所示,3σ准则去噪最大化了DCNN模型的预测精度。为了验证预测性能最好的模型(带3σ去噪的DCNN)的泛化能力,实验二仍然采用3σ准则去噪,应用3σ准则去噪时,3个模型的参数和结构与实验一一致。通过不同的数据集验证了模型的泛化能力。
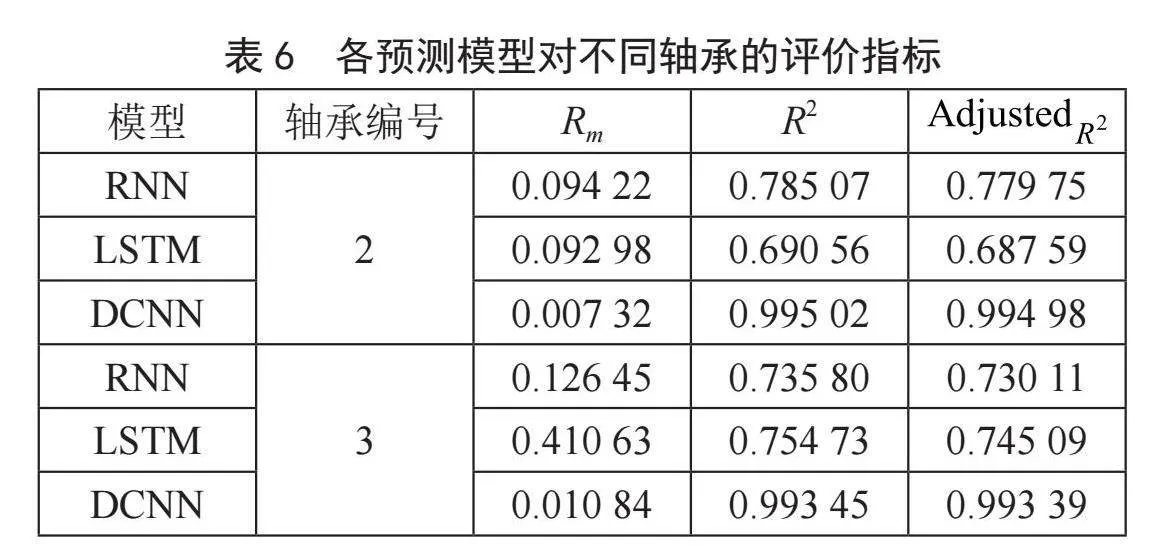
各模型的评价统计如6表所示,不同轴承的最佳评估指标值以粗体显示,所有这些评价指标都是通过DCNN实现的。
由表可知RNN和LSTM的评价指标值与DCNN模型存在较大差距;也就是说,预测结果是最差的,同时与轴承1的评价指标也有较大出入反映出其泛化能力也较弱。
表6的综合分析结果表明,RNN和LSTM的预测能力较差,DCNN对于不同退化趋势的轴承可以获得较好的预测结果,即DCNN的泛化能力最好。
3.3" 结果分析
实验一的结果分析,如表3至表6所示,表明DCNN模型的预测评价指标值最接近理想值;因此,DCNN模型的预测精度最高。通过3σ准则去噪预处理,提高了模型的预测评价指标值,表明3σ准则去噪效果最好。因此,结合DCNN模型的3σ准则去噪预处理方法对3个评价指标进行了优化,最优值为Rm = 0.005 25,R2 = 0.997 62, = 0.997 60。
实验二的结果分析,如表6所示,比较了每个模型的相应评价指标值。RNN、LSTM模型的相应评价尺度变化较大,表明RNN、LSTM严重依赖数据集,易受数据结构的影响,泛化能力弱。对应于DCNN模型的每个评估指标的值的变化最小。这一发现表明,该模型对数据集具有很强的适应性和最好的泛化能力。DCNN模型预测的评估指数值的范围如下:Rm (0.005 25,0.010 84)、R2 (0.993 45,0.997 62)、 (0.993 39,0.997 60),DCNN模型的变异范围最小,泛化能力最好。
4" 结" 论
本文提出了一种基于神经网络理论的轴承RUL预测方法,该方法预测能力强,泛化能力强。通过3σ准则法有效地去除了数据中的粗监测误差,提高了模型预测精度,得到的评价指标值比其他去噪方法得到的结果更接近理想结果。构造了由三个卷积层和两个全连通层组成的DCNN模型。并通过模型验证实验表明,基于3σ准则和分层抽样结合DCNN的去噪方法具有最高的预测精度和最强的泛化能力。
参考文献:
[1] 梁敏健,彭晓军,刘德阳.基于一维卷积神经网络的自动扶梯机械故障分类研究 [J].测控技术,2022,41(7):87-92+110.
[2] KHAN S,YAIRI T. A Review on the Application of Deep Learning in System Health Management [J].Mechanical Systems and Signal Processing,2018,107:241-265.
[3] KUNDU P,DARPE A K,KULKARNI M S. Weibull Accelerated Failure Time Regression Model for Remaining Useful Life Prediction of Bearing Working Under Multiple Operating Conditions [J].Mechanical Systems and Signal Processing,2019,134:106302[2023-06-10].https://doi.org/10.1016/j.ymssp.2019.106302.
[4] 关鹏,张毅.自动扶梯轴承健康指标提取及剩余寿命预测方法研究 [J].机电工程,2022,39(2):202-209.
[5] LEE J,WU F J,ZHAO W Y,et al. Prognostics and Health Management Design for Rotary Machinery Systems—Reviews, Methodology and Applications [J].Mechanical Systems and Signal Processing,2014,42(1-2):314-334.
[6] LEI Y G,LI N P,GONTARZ S,et al. A Model-Based Method for Remaining Useful Life Prediction of Machinery [J].IEEE Transactions on Reliability,2016,65(3):1314-1326.
[7] 杜泽厚.基于深度学习的轴承健康因子构建及寿命预测研究 [D].青岛:青岛科技大学,2022.
[8] QIAN Y N,YAN R Q,GAO R X. A Multi-Time Scale Approach to Remaining Useful Life Prediction in Rolling Bearing [J].Mechanical Systems and Signal Processing,2017,83:549-567.
[9] 郑琪,赵春晖.轴承磨损阶段划分与分段剩余寿命估计方法 [J].控制工程,2022,29(4):593-599+636.
[10] LEI Y G,LI N P,GUO L,et al. Machinery Health Prognostics: A Systematic Review from Data Acquisition to RUL Prediction [J].Mechanical Systems and Signal Processing,2018,104:799-834.
作者简介:张浩(1983—),男,汉族,江苏南京人,高级工程师,硕士研究生,研究方向:机械设计。