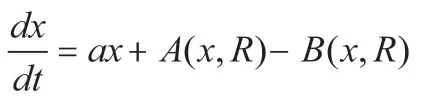
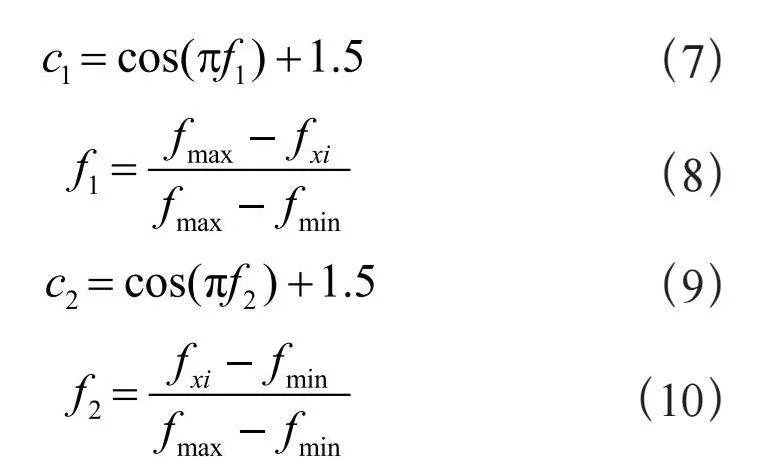
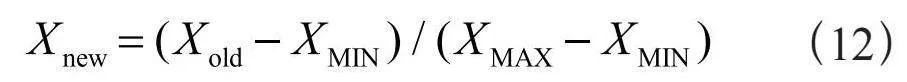
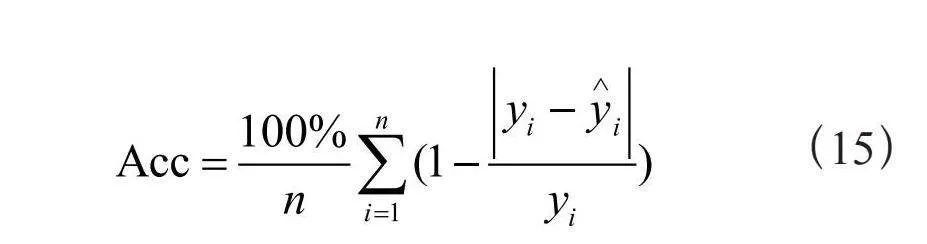
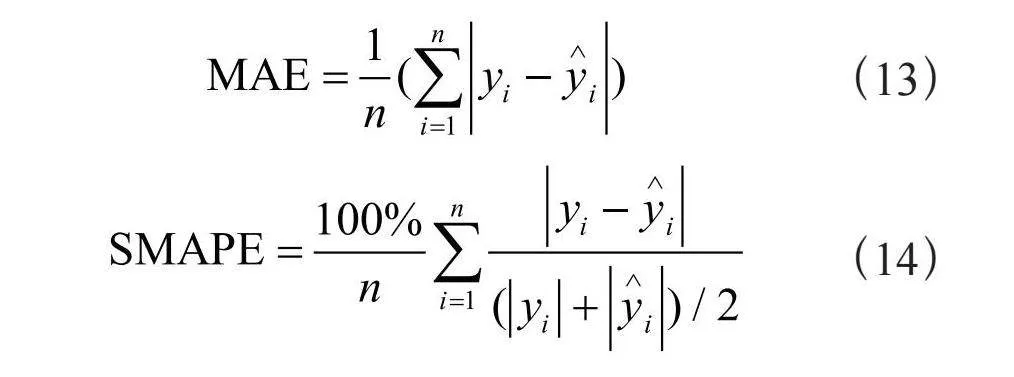

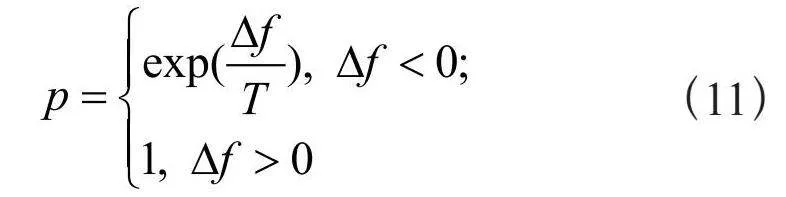
摘" 要:土壤重金属含量预测是土壤污染治理的重要一环,为提高预测准确性,文章提出一种基于COPSO-GRNN的土壤重金属含量预测模型。该模型针对广义回归神经网络(GRNN)的平滑因子难以确定的问题,使用余弦优化粒子群算法(COPSO)对其进行优化,优化过程中除了为种群个体增加小种群比较策略之外还采用了余弦加速系数来扩大搜索范围并避免陷入局部最优,之后引入适应准则来提高算法收敛速度。对该模型与几种常见的土壤重金属含量预测模型进行对比实验,实验结果表明该模型的预测值更接近于真实值,具有更好的预测性能。
关键词:土壤重金属含量预测;广义回归神经网络;余弦优化粒子群算法;参数优化
中图分类号:TP183;TP39 文献标识码:A 文章编号:2096-4706(2024)09-0153-05
Prediction Model for Soil Heavy Metal Content Based on COPSO-GRNN
CAO Wenqi
(Information Engineering Institute, Wuchang Institute of Technology, Wuhan" 430065, China)
Abstract: The prediction of soil heavy metal content is an important part of soil pollution control. To improve the accuracy of prediction, this paper proposes a prediction model for soil heavy metal content based on COPSO-GRNN. In response to the problem that it has difficulty in determining the smoothing factor of generalized regression neural networks (GRNN), the model uses cosine optimization particle swarm optimization (COPSO) for optimization. In addition to adding a small population comparison strategy to the population, it also uses cosine acceleration coefficient to expand the search range and avoid falling into local optima during the optimization process. Then, an adaptation criterion is introduced to improve the convergence speed of the algorithm. Comparative experiments are conducted between this model and several common prediction models for soil heavy metal content. The experimental results show that the predicted values of this model are closer to the true values and has better predictive performance.
Keywords: the prediction of soil heavy metal content; GRNN; COPSO; parameter optimization
0" 引" 言
随着工业化的发展,我国的土壤重金属污染问题愈发严重[1],但是由于人力、物力等条件的限制,往往难以做到对污染区域土壤重金属含量进行全面检测,因此选用有效的方法对未知区域的土壤重金属含量进行预测是一项重要的研究。
广义回归神经网络模型(GRNN)是一种无须反向迭代训练的前馈型神经网络[2],相较于BP神经网络等具有收敛速度快、非线性逼近能力强等优势,目前已被广泛应用到各个行业的数据预测上,如水质预测[3]、光伏发电量预测[4]等,因此将该模型用于土壤重金属含量预测是可行的。虽然在使用GRNN进行数据预测时能够取得较好的效果,但由于其平滑因子难以确定,容易导致预测性能不够稳定[5]。研究人员通常采用智能优化算法对GRNN中的平滑因子进行寻优以提高GRNN的预测性能,在算法的选择上,粒子群算法相较于其他智能优化算法在解决目标优化问题时具有更快的收敛速度与更好的收敛结果[6],但随着问题复杂性的增加,其优化结果容易陷入局部最优。
本文在GRNN与PSO的基础上提出了一种COPSO-GRNN模型,该模型首先在PSO的迭代过程中引入了余弦加速系数来进行个体位置的计算,同时利用小种群比较策略来让个体向周围方向进行发散以扩大搜索范围,之后引入适应准则进行迭代前后适应度值的比较来获得较优的位置信息,最后将该寻优方式用于确定GRNN的平滑因子最优取值,以此来克服GRNN与PSO本身存在的不足,从而在进行土壤重金属含量预测时获得更好的预测效果。
1" 基本原理
1.1 广义回归神经网络
广义回归神经网络(GRNN)是一种具有较好的非线性逼近能力的四层前向传播神经网络[2],其结构如图1所示,数据输入网络后依次经过输入层、模式层、求和层、输出层后得到输出结果。
1)输入层,将输入数据传递到模式层,节点数为输入数据的特征维度。
2)模式层,一般使用高斯函数对输入数据进行处理,节点数为训练样本的个数,具体的计算公式为:
其中,xi为训练样本,xj为学习样本,σ为平滑因子。
3)求和层,假设输出样本维度为k,则该层节点数为k+1,其中一个节点输出SD为模式层输出的算术和,其余节点输出SNi均为模式层输出的加权和,具体的计算式为:
其中,wij为加权系数;
4)输出层,该层节点数为输出样本维度,主要根据求和层求出的算术和与加权和进行计算输出,计算式为:
虽然GRNN无须进行网络训练,但模式层的平滑因子σ对网络的性能影响较大[7],平滑因子过大或过小会分别导致网络出现欠拟合与过拟合的现象,而在实验中通常难以将平滑因子设定至较优的数值,因此若想获得较好的网络性能,往往选用高效的智能优化算法对平滑因子进行寻优。
1.2" 粒子群算法
粒子群算法(PSO)于1995年被Kennedy等人提出[8],该算法受到自然界中鸟群捕食这一群体性行为的启发,将问题的不同解作为鸟群个体的位置信息,最优解作为食物的位置信息,个体间通过位置信息的交换进行移动,从而发现食物的位置,即问题的最优解。
假设种群中存在m个不同的个体,在第t次种群位置的迭代过程中,每个个体的移动速度计算公式和位置更新公式为:
其中" 和" 分别为第i个个体在第t次迭代时的移动速度和位置信息,w为惯性系数,c1和c2均为加速系数,r1和r2为0到1之间的随机数, 是第i个个体在第t次迭代时的历史最优位置信息,gbestt是该种群在第t次迭代时的历史最优位置信息。
虽然PSO在处理寻优问题时的高效性已得到证明,但与大多数元启发式算法一样,随着问题复杂度的提高,收敛精度降低、局部信息利用与全局信息搜索难以平衡等问题依旧存在[9],这也是需要对该算法进行改进的方向。
2" COPSO-GRNN模型
2.1" 余弦优化粒子群算法
本文提出的余弦优化粒子群算法(COPSO)在PSO的基础上进行了三个方面的改进:应用小种群比较策略扩大个体搜索范围、采用余弦加速系数更新个体学习方式以及利用适应准则进行个体位置更新前后比较。
2.1.1" 小种群比较策略
小种群比较策略在每次迭代时首先围绕种群的每个个体随机生成一个新的小种群,然后在小种群中进行最优位置的选择,并将该最优位置信息与个体的历史最优位置进行比较。假设个体i的历史最优位置信息和对应的适应度值分别是" 和 ,小种群的最优位置信息和对应的适应度值分别是" 和 ,那么每次迭代过程中,若" 小于 ,则" 将作为新的" 存在,反之则不发生变化。
通过这种方式,可以让个体在每次迭代过程中探索自身周围的区域,扩大搜索范围以增加种群的多样性,避免落入局部最优位置。
2.1.2" 余弦加速系数
在个体移动速度的更新公式中,存在参数c1和c2这两个加速系数,分别表示对个体和种群最优位置信息的学习速度,然而每个个体的位置优劣不同,个体学习的量也应随之改变,因此传统的c1和c2采用固定值不利于个体的全局寻优。
COPSO中的c1和c2采用基于余弦的变化方式,根据个体自身的适应度值大小来决定学习的速度,具体的计算式为:
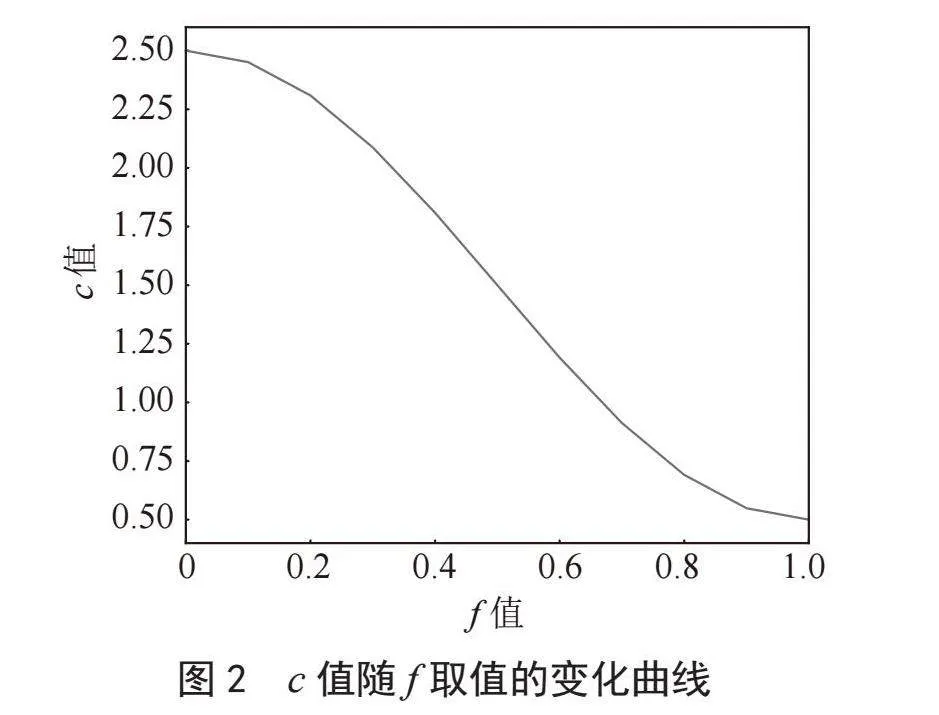
其中fxi为当前个体的适应度值,fmax和fmin分别为当前种群的最优适应度值和最差适应度值,c1和c2随f取值变化的曲线如图2所示。
结合图2以及c1和c2的计算公式可以得知当个体自身适应度值接近种群的最优时,f1取值越小,对应c1取值越大,那么个体本身将会更多地向周围进行探索,降低向种群最优个体学习的比例,以此来避免陷入局部最优;而当个体的适应度值越小时,f2的取值越小,c2取值越大,此时个体将更多地向种群最优个体进行学习,以此来加快其收敛速度。
2.1.3" 适应准则
适应准则主要通过比较更新前后的个体适应度来计算接受新的位置信息的概率,避免由于位置更新后适应度值的降低导致收敛速度降低的情况发生,概率的计算公式如下:
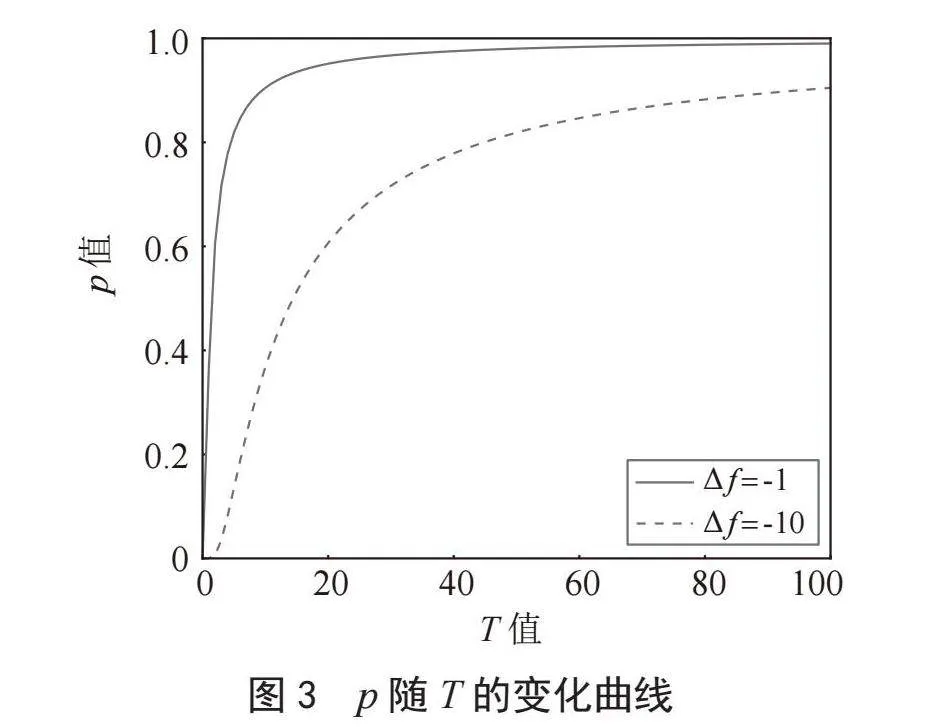
其中∆f为位置更新前后适应度的差值,T为迭代次数,初始值为0,随着迭代过程不断增加。当∆f大于或等于0时,p取值为1,即若更新后的位置信息优于更新前,将直接接受更新后的位置信息,而当∆f小于0时,p随T的变化曲线如图3所示。
由图3可以看出,迭代前期T取值较小,p取值较小,即个体将会以较小的概率接受更新后适应度较低的位置信息,以此加快收敛速度,而到了迭代后期,个体的收敛情况相对较好,出现更新前后差值较大的概率较小,那么个体接受适应度较低的位置信息的概率也会增大。此外当适应度差值∆f取值越大时,接受该位置信息的概率越低,这主要是为了保持较好的位置信息,从而加快其收敛速度。
2.2" COPSO-GRNN模型的建立
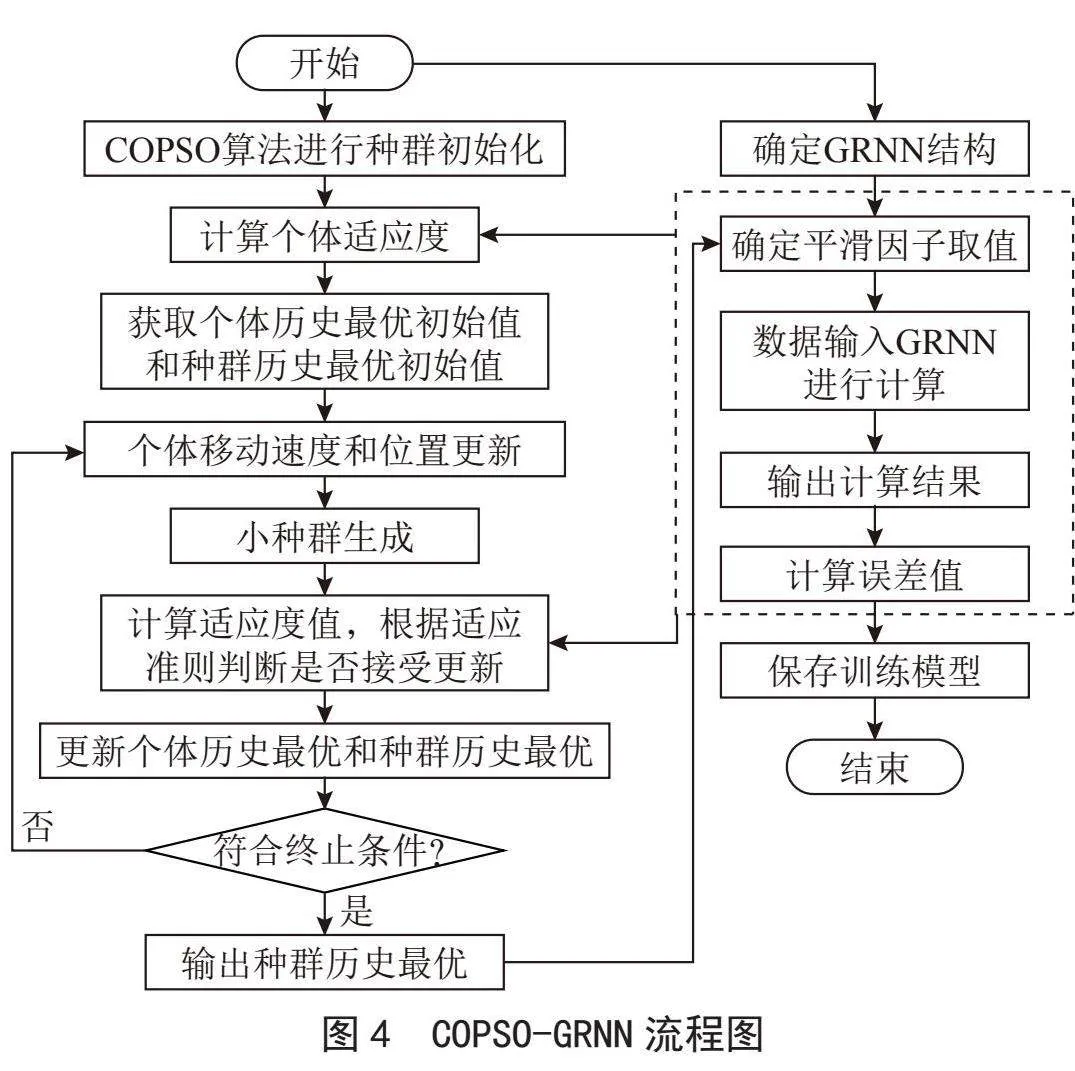
在COPSO和GRNN的基础上建立COPSO-GRNN模型,建模步骤如下:
1)以GRNN中平滑因子值作为COPSO算法个体的位置信息进行种群初始化。
2)将输入数据输入赋值不同平滑因子的GRNN,计算输出值与目标值之间的均方误差,并将其作为每个个体的适应度值。
3)将个体的位置信息作为个体的历史最优位置初始值,比较不同的个体适应度值来获取种群的历史最优位置初始值。
4)进行个体移动速度和位置信息的更新。
5)在每个个体周围生存小种群。
6)计算更新后的适应度值,根据适应准则判断是否接受新的位置信息。
7)通过适应度值的比较来对个体的历史最优位置和种群的历史最优位置进行更新。
8)重复步骤4)到步骤7),当满足停止迭代条件或达到最大迭代次数时停止迭代,输出种群历史最优位置信息,模型训练结束。
COPSO-GRNN的流程图如图4所示。
3" 实验与结果分析
3.1" 数据选择与处理
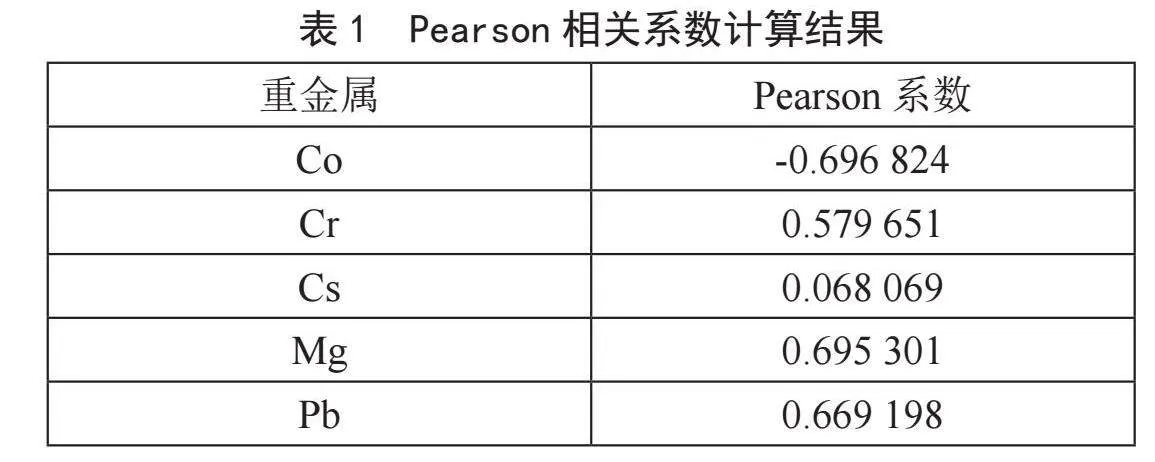
为验证COPSO-GRNN模型在土壤重金属含量预测上的有效性,选用宁夏银川市市区表层土壤重金属元素数据集作为实验数据[10],该数据集总共96组,随机选择其中的24组作为测试数据集,72组作为训练数据集。另外数据集中包含的重金属分别为Co、Cr、Cs、Mg、Pb、Ti,选取重金属Ti的含量作为待预测的输出特征,然后将其他重金属与重金属Ti进行相关性分析来确定模型的输入特征,本实验采用Pearson系数作为相关性分析依据,具体的计算结果如表1所示,根据计算结果,选取Pearson相关系数绝对值大于0.5的重金属Co、Cr、Mg、Pb作为模型的输入特征。
实验前与实验后需要对输入数据与输出数据分别进行归一化与反归一化处理,本实验采用最大最小归一化方法,公式为:
其中,Xold为原始数据,XMAX与XMIN分别为原始数据中的最大值与最小值。
3.2" 实验结果与分析
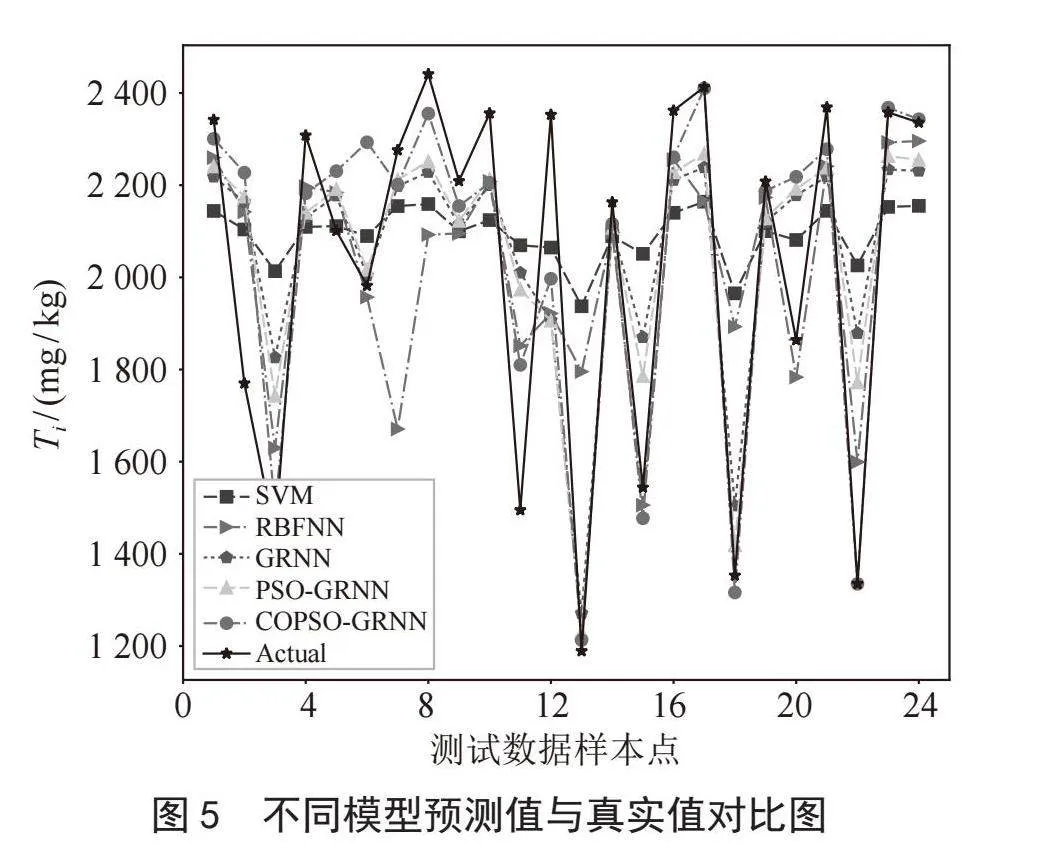
本实验选用支持向量机(SVM)、径向基神经网络(RBFNN)、GRNN、PSO优化GRNN(PSO-GRNN)以及COPSO-GRNN进行对比实验,其中SVM的相关参数设置为默认值,RBFNN的学习率与迭代次数分别设置为0.01和100,其他模型的参数设置与表1中的参数设置保持一致。将五种模型进行迭代训练,它们的最终预测值与真实值之间的差值对比情况分别如图5所示。
在图5中可以看到与真实值重合最高的是COPSO-GRNN预测值的曲线,这两条曲线的走势基本一致,部分样本点出现了重合,说明COPSO-GRNN的预测值较其他模型更接近真实值。
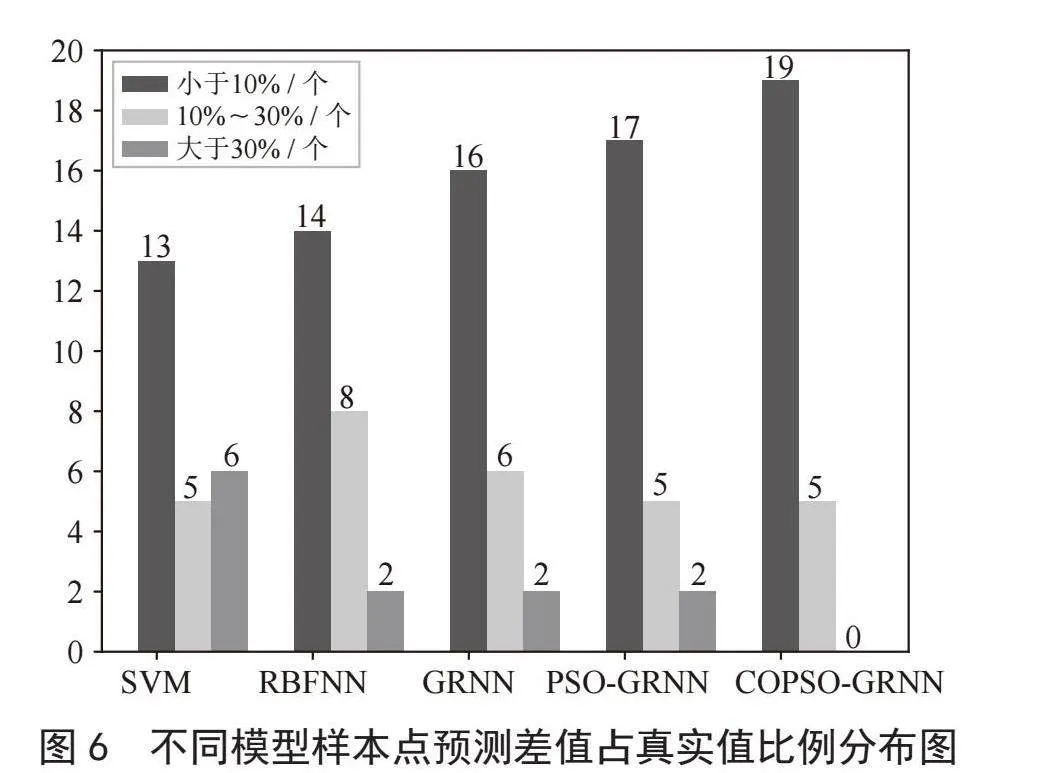
另外针对24个预测样本点,分别计算了每个预测点的预测值和真实值之间的差值占真实值的比例,并对不同比例区间的预测点的数量进行了统计,统计结果如图6所示。
在图6中,小于10%的样本个数越多,说明模型预测值与真实值之间差距越小,COPSO-GRNN在这个区间内点的数量最多,总共有19个,而在10%~30%以及大于30%的区间内数量要少于另外四种模型,说明CBSA-GRNN预测值与真实值之间的差距最小。
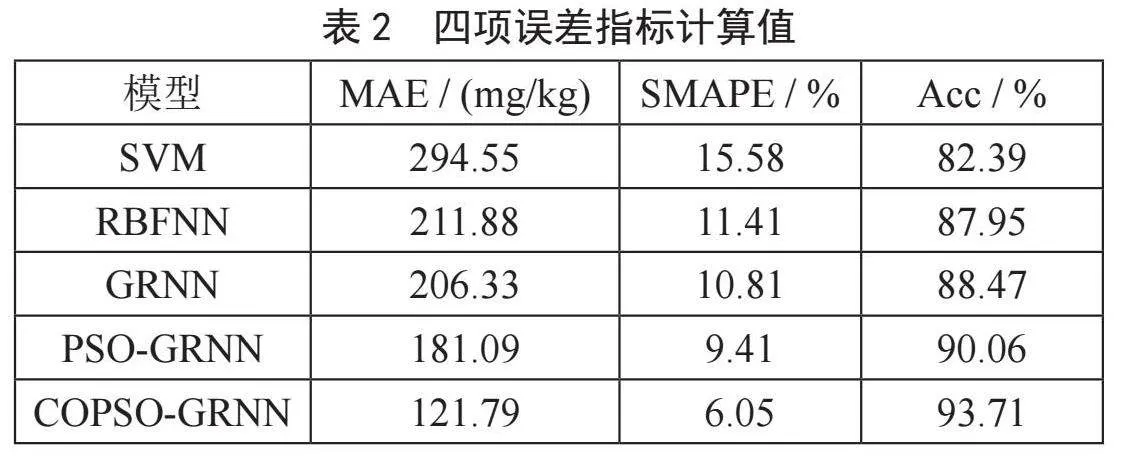
除上述两种实验结果分析外,还使用平均绝对误差(MAE),对称平均绝对百分比误差(SMAPE)以及准确率(Acc)三项误差指标对五种模型的预测效果进行评估,这三项误差指标的计算式为:
其中,yi为真实值, 为预测值,n为预测样本数量,MAE与SMAPE计算结果越小表示预测误差越小,Acc计算结果越大表明预测值越接近真实值。表2给出了五种模型在四项误差指标下的计算结果。
由表2可以看到,在MAE与SMAPE这两项误差指标上,COPSO-GRNN的计算结果最小,而在误差指标Acc的计算结果中,COPSO-GRNN相较于其他几种模型计算结果最大,说明COPSO-GRNN的三项误差指标结果计算值较其他模型更优。
综合上述三项实验结果及分析可以得出结论,本文提出的COPSO-GRNN在进行土壤重金属含量预测时较其他四种对比模型预测精度更高,预测效果更好。
4" 结" 论
本文提出一种COPSO-GRNN模型用于土壤重金属含量预测,其中COPSO是在PSO的基础上引入了小种群比较策略、余弦加速系数以及适应准则,在提高种群内部信息利用率的同时增强了算法的全局搜索能力,然后将COPSO运用到GRNN平滑因子的寻优上过程,最后将COPSO-GRNN与其他四组模型进行土壤重金属含量预测对比实验,证明了该模型较其他对比模型预测准确性更高,具有更好的预测性能。对COPSO-GRNN模型的结构进行改进以提高其预测性能,并将其应用到更多的实际问题上,是接下来将进一步研究的内容。
参考文献:
[1] 陈雅丽,翁莉萍,马杰,等.近十年中国土壤重金属污染源解析研究进展 [J].农业环境科学学报,2019,38(10):2219-2238.
[2] SPECHT D F. A General Regression Neural Network [J].IEEE Transactions on Neural Networks,1991,2(6):568-576.
[3] 徐睿,张晓斌,薛鹏松.基于改进的GRNN-Markov水质预测模型研究及应用 [J].灌溉排水学报,2022,41(S1):104-110.
[4] 卞海红,孙健硕.基于典型气象周的GRNN光伏发电量预测模型 [J].电力工程技术,2021,40(5):94-99.
[5] LIANG Y,NIU D X,HONG W C. Short Term Load Forecasting Based on Feature Extraction and Improved General Regression Neural Network Model [J].Energy,2019,166(1):653-663.
[6] 李轩宇,张兆军,许钊雄.基于改进PSO算法的B样条曲线拟合 [J].传感器与微系统,2022,41(7):130-133+138.
[7] 高媛,阳媛,凌启东.基于麻雀算法优化GRNN的三维定位算法 [J].计算机工程与设计,2022,43(11):3149-3158.
[8] Kennedy J,Eberhart R. Particle Swarm Optimization [C]//Proceedings of ICNN 95-international Conference on Neural Networks.Perth:IEEE,1995:1942-1948.
[9] 杜鑫钰,陈军锋,薛静,等.基于PCA-PSO-GRNN模型的冻融期土壤蒸发预报 [J].节水灌溉,2021(1):14-19.
[10] 张明鑫,李浩.宁夏银川市市区表层土壤重金属元素数据集 [J].全球变化数据学报:中英文,2018,2(2):198-204+321-327.
作者简介:曹文琪(1995—),男,汉族,湖北黄冈人,高级工程师,硕士研究生,研究方向:机器学习算法及其应用。