





摘" 要:针对起伏地形环境下雷达布站存在探测盲区难以精确求解组网优化布站性能指标的问题,基于实地数字高程模型数据,提出使用网格矩阵法进行求解,并对网格分辨率变化对精准度的影响进行了探索研究。仿真结果表明,网格分辨率与求解精度和平均计算耗时均成正比,当网格分辨率选择恰当时,性能指标与标准值之间的误差小于5%,为精确求解组网优化布站性能指标提供了新方法。
关键词:网格矩阵法;雷达组网;布站性能指标;优化布站
中图分类号:TN95" 文献标识码:A" 文章编号:2096-4706(2024)11-0001-07
Research on Solving Performance Index of Radar Networking Optimization of Station Layout Based on Grid Matrix Method
LIU Geng1, LI Xiaoyi2, FENG Ketao1, YANG Gang1, LIU Bo1
(1.Unit 31306 of PLA, Chengdu" 610036, China;
2.Communication Sergeant School of Army Engineering University, Chongqing" 400035, China)
Abstract: Aiming at the problem that it is difficult to accurately solve the performance index of networking optimization of station layout due to the existence of detection blind area in radar station layout in the undulating terrain environment, based on the field digital elevation model data, the grid matrix method is proposed to solve it, and the influence of grid resolution change on accuracy is explored and studied. The simulation results show that the grid resolution is directly proportional to the solution accuracy and the average calculation time. When the grid resolution is properly selected, the error between the performance index and the standard value is less than 5%, which provides a new method for accurately solving the performance index of networking optimization of station layout.
Keywords: grid matrix method; radar networking; performance index of station layout; optimization of station layout
0" 引" 言
现代战争中,电磁环境日益复杂,国土防空预警体系面临的挑战日益严峻[1],雷达系统获取信息的有效性对防御系统至关重要[2-4]。当前,雷达面临“电磁干扰、反辐射导弹、隐身技术和超低空突防”四大威胁[5]。雷达组网进行综合部署,可以构成全方位、立体化、多层次的防御体系,实现雷达间的战术协同,提高组网雷达的生存能力和探测能力[6],在应对“四大威胁”中发挥着越来越重要的作用[7,8]。
雷达组网优化布站是雷达组网应用的重要支撑,通过对组网雷达的搜索性能、阵地条件、电磁环境、任务要求、生存能力等各种因素的系统规划,在指定作战区域内实现有限雷达资源的合理布局,优化雷达网系统作战效能[9]。雷达组网优化布站问题,本质上属于多维优化问题,近年来兴起的粒子群算法[1]、猴群算法[10]、遗传算法[11]、蛙跳算法[12]等群体智能优化算法为解决该类问题提供重要工具。文献[1]和[13]均对雷达组网优化布站性能指标进行了描述,是雷达组网优化布站数学模型的基础,其求解的准确度直接制约后续组网优化布站。从文献资料看,未见相关文献对雷达组网优化布站性能指标进行精准化研究。
雷达探测距离是反映雷达性能的关键指标,对雷达网的优化部署具有重要作用[14],通常情况下其探测范围并非是一个规则圆,尤其受地形遮蔽因素影响较大[15,16],会直接引起雷达探测盲区,而文献[1,5,17,18]忽略了地形遮蔽引起的雷达探测盲区对求解过程的影响,不够贴合实际,直接制约对雷达组网布站的科学性。针对以上问题,本文基于雷达选址的数字高程模型(Digital Elevation Model, DEM)实际地形,考虑地物对雷达电磁波的遮蔽所引起的覆盖盲区,借鉴文献[19]的研究思路,提出使用网格矩阵法提高雷达组网优化布站性能指标求解的精确度,能够为后续进行雷达组网科学布站奠定基础。
1" 雷达布站组网性能指标
复杂态势下,雷达组网优化布站需要综合考虑不同任务需求,兼顾多种指标对雷达组网进行优化布站。常用的雷达布站组网性能指标包括:空域覆盖系数ρ,反映空域有效覆盖范围的大小及雷达网探测隐身目标的能力[20];空域覆盖重叠系数μ,反映雷达探测区域在责任区的重叠程度;重点区域探测系数θ,反映雷达探测重点区域占总责任区的比重;频率干扰系数λ,反映相邻雷达的同频干扰程度;资源利用系数τ,反映覆盖区域既要有一定的冗余度又要兼顾资源利用。常见的方法是通过加权求和的方式,将多个指标转化为一个指标进行研究[9]。
2" 雷达组网优化布站数学模型
2.1" 约束条件
为有效实现相互补盲,文献[21]对相邻雷达之间的距离约束使用衔接系数描述[1]:
(1)
式中:SCH为相邻雷达的重叠探测面积;SrH为探测半径较小的雷达的探测面积;d为相邻雷达之间的距离;rH为较小的探测半径,RH为较大的探测半径。
2.2" 数学模型
雷达组网优化布站的数学模型为[1]:
(2)
式中:k1~k5为加权系数,表征各指标对雷达网性能的重要程度。
3" 雷达组网优化布站性能指标量化求解方法
当考虑在高低起伏的地形环境下对雷达布站时,难以使用文献中的数学公式对其进行准确描述:一方面,起伏地形对雷达电磁波有遮挡,存在覆盖盲区;另一方面,防区通常是一个形状不规则的连续区域。综上分析,要直接确定可布站区域和求解空域覆盖系数ρ、重叠覆盖系数μ、重点区域探测系数θ、资源利用系数τ并不容易,使雷达网布站的数学模型难以准确建立。文献[13]紧贴实际地形,提出了改进的雷达布站数学模型,通过建立离散的布站网格剔除不可达地区的影响,提高了布站的准确度,但未考虑起伏地形对雷达有效覆盖区域的遮挡,难以准确求解出ρ、μ、θ和τ。本文引入实地DEM数据,并提出网格矩阵法求解雷达组网优化布站性能指标问题。
3.1" 起伏地形模型
DEM是地表形态的数字化表达,蕴含了丰富的地学应用分析所必需的地形地貌信息[22],坡度、坡向、地貌起伏、地势走向等地貌特性均可在DEM的基础上派生。考虑到DEM规则网格模型具有模型简单、易于处理的优点,本文选用规则网络模型进行研究[23]。
3.2" 方法步骤
本文提出网格矩阵法求解雷达组网优化布站性能指标问题,主要分为DEM数据预处理、雷达盲区确定和雷达组网优化布站性能指标求解三个步骤。
3.2.1" DEM数据预处理
DEM数据预处理的步骤如下:
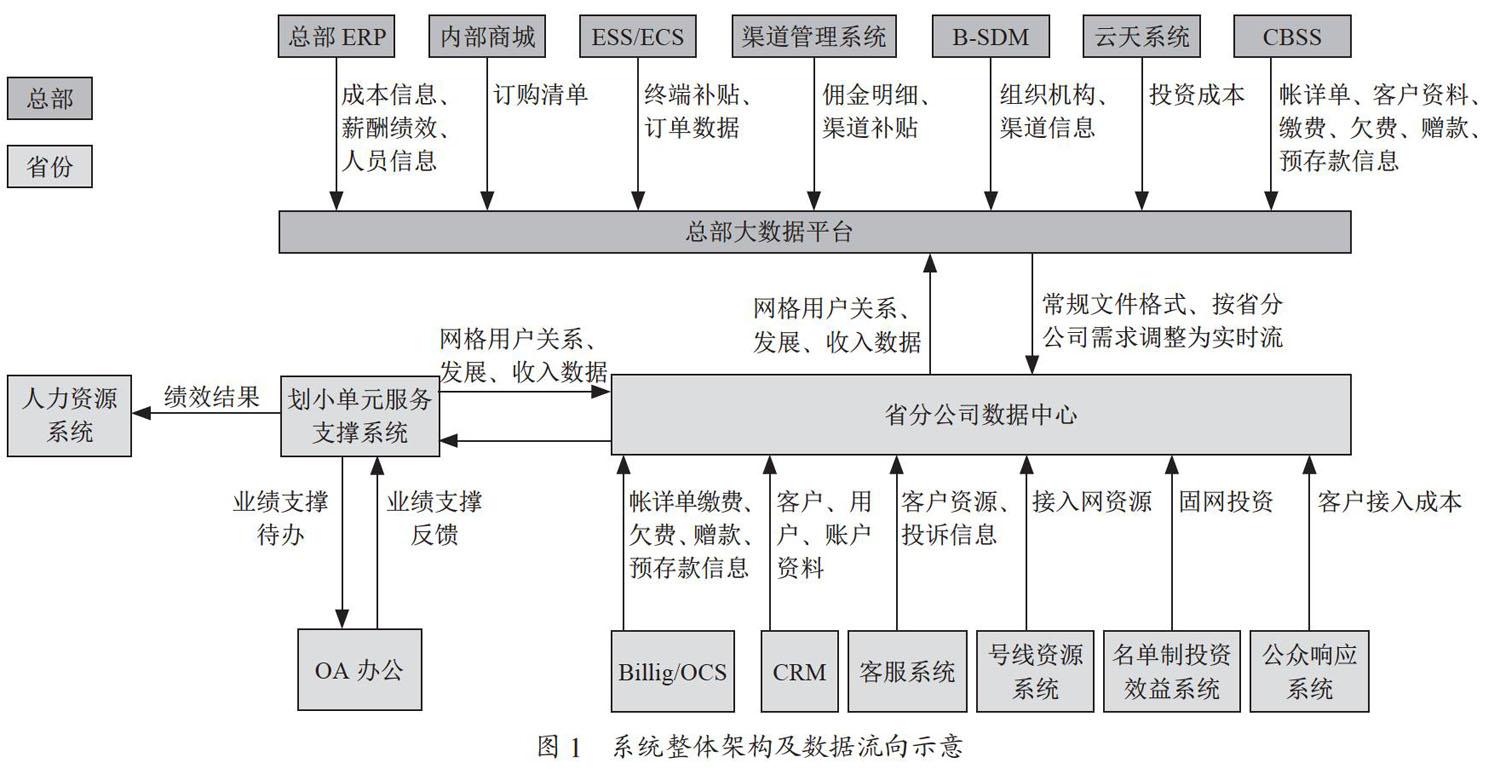
1)导入雷达布设地域周边的DEM数据,如图1所示。
2)高程清洗。采用“高程清洗”[19]的方法,降低计算冗余。设雷达天线中心点坐标为G = (x0,y0,z0),地域周边的DEM数据为W = (xi,yj,zij),定义f(i,j)为标记函数,其中:
(3)
设f (i,j)中1和0的数量分别为N1和N0,则相对传统最大斜率法减少的计算冗余比例为:
(4)
3)高差改正。为抵消地球曲率和大气折光差的影响,使用地球曲率补偿公式对高程进行高差改正[24]:
(5)
式中:δh为高差改正系数;d为地物点与G点之间的水平距离,K为大气折光差系数,RE为地球半径。
若h为地物点的DEM原始海拔高程值,则高差改正后的高程为:
(6)
3.2.2" 雷达盲区确定
对雷达布设地域周边的DEM数据进行预处理后,为准确求解出某一方位上雷达电磁波遭起伏地形遮蔽影响引起的探测盲区,需求解出该方位的最大斜率遮蔽角,如图2所示,O为雷达天线中心点位置,A为天线在地球表面的投影点,O为在设定高度H条件下求解的雷达覆盖区域的圆心,h0 = OA为天线海拔高度。E1~E5分别为离散的DEM网格交点,由于E1、E5海拔高度低于O,显然不会对雷达电磁波在海拔高度H平面造成遮蔽;E2、E3、E4为该方向的遮蔽点,E2、E3、E4分别为OE2、OE3、OE4延长线与H高度平面的交点,、、 分别为对应的遮蔽角。求出该方向的最大斜率遮蔽角" 后,即可确定起伏地形引起的雷达盲区,具体步骤为:
1)计算基准遮蔽角。如图3所示,OE为地球球心,B、C为覆盖圆上的过点O对称的两个点,B、C分别为其在地球表面的投影点。则H = BB为设定的雷达探测高度,D = OB为雷达最大有效覆盖距离,R = OB为在高度H条件下雷达有效覆盖区域的半径,RE = AOE为地球半径, 为O与B之间的地表距离。
根据余弦定理,有:
(7)
则在高度H下雷达的覆盖范围半径为:
(8)
水平距离OB为:
(9)
如图4所示,H为高度H经过式(6)高差改正后的高程,θs为基准遮蔽角,则有:
(10)
2)确定各个方向的最大斜率遮蔽角。首先以雷达天线中心点O为圆心,通过标记函数f (i,j)从W中挑选出对点O有遮蔽的点;然后寻找各方位上的最大斜率遮蔽点集合 ,其对应的最大斜率遮蔽角集合为 ,如图5所示。
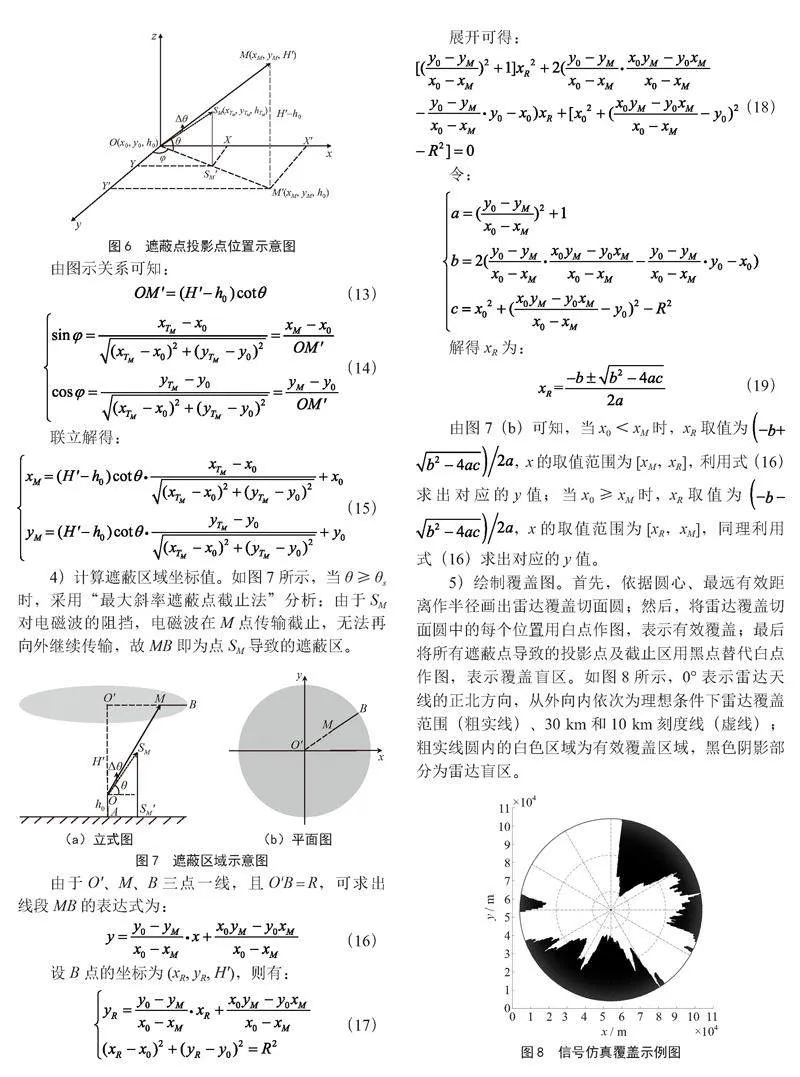
3)确定最大斜率遮蔽点在雷达探测高度的投影点位置。如图6所示,天线中心 、最大斜率遮蔽点" 已进行高差改正,M(xM, yM, H′)为因最大斜率遮蔽点SM阻挡在H高度平面的投影点,SM、M分别为SM、M在天线高度平面的投影点;φ为OM与y轴之间的夹角。考虑电磁波绕射影响,计算遮蔽角时需增加角度修正量Δθ [25]:
(11)
式中:c为光速,f为雷达工作频率,dL为O点与SM之间的斜距离。实际应用中,修正后的最大斜率遮蔽角计算公式为[26]:
(12)
由图示关系可知:
(13)
(14)
联立解得:
(15)
4)计算遮蔽区域坐标值。如图7所示,当θ≥θs
时,采用“最大斜率遮蔽点截止法”分析:由于SM对电磁波的阻挡,电磁波在M点传输截止,无法再向外继续传输,故MB即为点SM导致的遮蔽区。
由于O、M、B三点一线,且OB = R,可求出线段MB的表达式为:
(16)
设B点的坐标为(xR, yR, H),则有:
(17)
展开可得:
(18)
令:
解得xR为:
(19)
由图7(b)可知,当x0<xM时,xR取值为 ,x的取值范围为[xM,xR],利用式(16)求出对应的y值;当x0≥xM时,xR取值为 ,x的取值范围为[xR,xM],同理利用式(16)求出对应的y值。
5)绘制覆盖图。首先,依据圆心、最远有效距离作半径画出雷达覆盖切面圆;然后,将雷达覆盖切面圆中的每个位置用白点作图,表示有效覆盖;最后将所有遮蔽点导致的投影点及截止区用黑点替代白点作图,表示复盖盲区。如图8所示,0°表示雷达天线的正北方向,从外向内依次为理想条件下雷达覆盖范围(粗实线)、30 km和10 km刻度线(虚线);粗实线圆内的白色区域为有效覆盖区域,黑色阴影部分为雷达盲区。
3.2.3" 雷达组网优化布站性能指标求解
雷达组网优化布站性能指标求解的步骤如下:
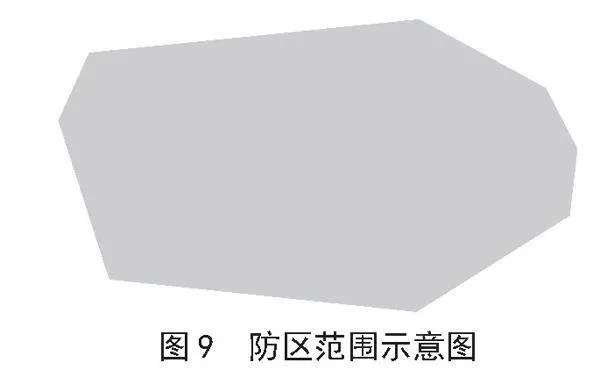
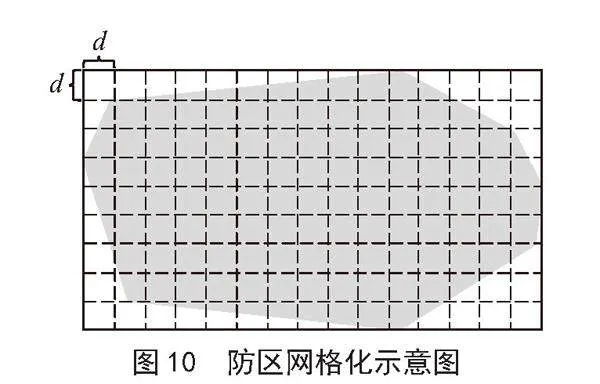
1)防区网格化。首先设定防区高度,确定防区范围,如图9所示。再按照经线和纬线方向,使用一个最小的矩形框将防区包裹起来,并使用等间隔为d的网格线对其进行分割,如图10所示。
2)防区描述矩阵。将图11中的每个网格进行统计:若浅灰色区域面积占比小于50%,则将相应位置的值置为0,表示该位置不在防区内;否则,值置为1,表示该位置属于防区。经过统计后,得到防区描述矩阵F,如图11所示。
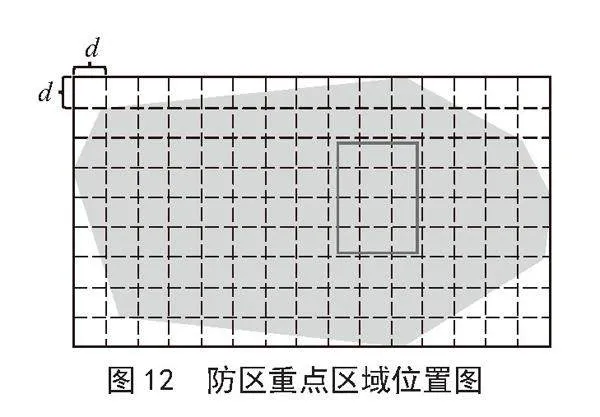
3)重点区域描述矩阵。如图12所示,本文设定黑色矩形框内的区域为重点区域。参照2)中防区描述矩阵的构建方法,构建重点区域描述矩阵Z,如图13所示。
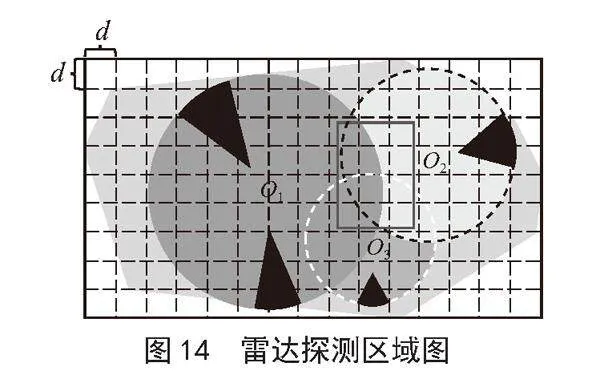
4)雷达探测区域描述矩阵。如图14所示,O1、O2和O3分别为三部雷达的部署点,其对应的探测区域分别为圆O1、圆O2和圆O3,深黑色扇形区域表示探测盲区。分别得到三部雷达探测区域描述矩阵为L1、L2和L3,如图15所示。
3.3" 程序实现
当只求某一高度层(即m = 1)的雷达布站组网性能指标时,可得到n部雷达总的探测区域描述矩阵:
(20)
空域覆盖系数可表示为:
(21)
式中:sum(sum(L~=0))为统计矩阵L中非零元素的总数,sum(sum(F==1))为统计矩阵F中元素为1的总数。
空域重叠覆盖系数可表示为:
(22)
式中:sum(sum(L>=2))为统计矩阵L中不小于2的元素的总数。
重点区域探测系数可表示为:
(23)
资源利用系数可表示为:
(24)
4" 仿真研究
分析文献[19]可知,网格分辨率与求解精度息息相关。为探讨网格分辨率对雷达组网优化布站性能指标量化的影响,本节设置实验进行仿真研究。仿真环境为Intel Core i7 2.8 GHz处理器,内存24 GB,使用MATLAB 2019b作为仿真平台。
4.1" 实验对象
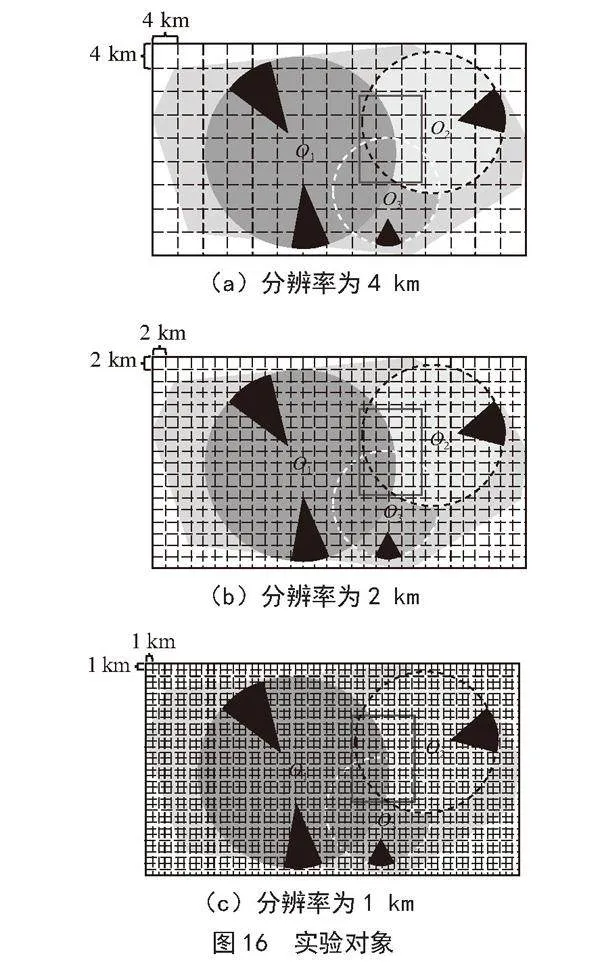
本文以某雷达组网实际覆盖图为研究对象,区域范围均为60 km×36 km,分别使用4 km、2 km和1 km的网格分辨率对该区域进行网格化分割,依次得到图16(a)(b)(c)。
4.2" 实验结果
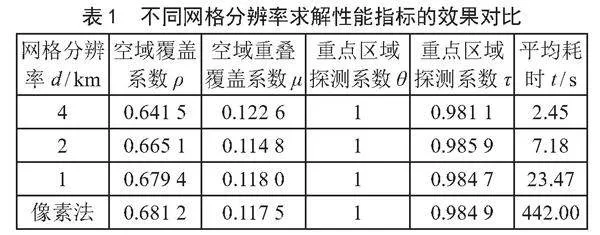
由于图16中的深黑色雷达盲区部分是不规则的,而软件Photoshop在计算不规则图形面积时具有精度高的优势[27],并在多个领域中应用广泛。本节采用本文方法和文献[28]使用的Photoshop像素法进行比较,计算得到的4个性能指标值和平均耗时结果,如表1所示。
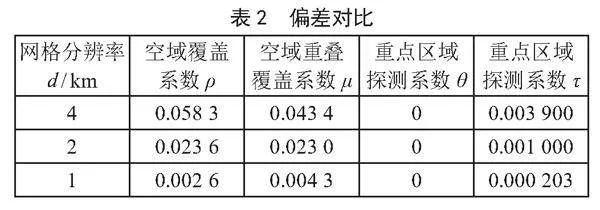
三种分辨率下计算得到的4个性能指标值,相对像素法计算结果的偏差如表2所示。
由表1可知,本文方法和像素法计算得到的4个性能指标值非常接近,且随着分辨率的提升,平均耗时逐渐增大,而像素法耗时最长。分析表2可知,随着分辨率提升,空域覆盖系数ρ、空域重叠覆盖系数μ和重点区域探测系数τ与像素法求得值的偏差依次降低,重点区域探测系数θ由于全覆盖,没有变化。表明提升网格分辨率可有效提高性能指标求解精度,但同时网格分辨率与计算耗时是一对矛盾:分辨率越高,则耗时越长;分辨率越低,则耗时越短。
5" 结" 论
本文针对雷达探测存在不规则盲区的实际,基于雷达布站周边区域DEM数据,提出网格矩阵法对雷达组网优化布站性能指标求解进行了研究,并通过实验分析了网格分辨率对求解雷达组网优化布站性能指标精度的影响。仿真结果表明,当网格分辨率选择恰当时,随着网格分辨率的提升,网格矩阵法求解值积极逼近像素法求解值,偏差在5%以内,且无须大量人工操作,耗时大幅减少。在实际应用中,可根据实际需求合理选择网格分辨率,同步考虑计算精度和耗时。
参考文献:
[1] 马艳艳,金宏斌,李浩,等.改进粒子群算法在雷达组网优化布站中的应用 [J].现代防御技术,2020,48(3):104-112.
[2] DELMARCO S P, DASGUPTA N, TOM V,et al. Modeling Radar Probability of Detection for a Randomly-located Mover on an Arbitrary Road Network [J].IEEE Systems Journal,2015,9(4):1208-1217.
[3] DYMOND K F,NICHOLAS A C,BUDZIEN S A,et al. Ionospheric-thermospheric UV Tomography: 2)Comparison with Incoherent Scatter Radar Measurements [J].Radio Science,2017,52(3):357-366.
[4] 胡磊,张凤奎,刘宝印,等.美国反导预警系统建设思考 [J].飞航导弹,2018(9):61-64.
[5] WANG X F ,CHEN M M. Application of Mathematical Model Based on Optimization Theory and Particle Swarm Algorithm in Radar Station Layout Optimization [J].Journal of Physics: Conference Series,2021,1848(2021):1-9.
[6] 潘伟.基于自适应遗传算法的雷达组网优化部署 [J].电子信息对抗技术,2013,28(4):34-38.
[7] 刘洁怡,张林让,赵珊珊,等.欺骗式干扰下组网雷达优化布站方法分析与仿真 [J].电子科技大学学报,2017,46(4):513-519.
[8] 崔树林,张翔宇,张光轶.多飞航导弹目标协同跟踪技术研究 [J].海军航空工程学院学报,2018,33(2):210-216+230.
[9] 马艳艳,金宏斌,李浩,等.雷达组网优化布站综述 [J].飞航导弹,2020(8):82-85.
[10] 崔玉娟.改进混沌自适应猴群算法在雷达组网优化部署中的应用 [J].海军工程大学学报,2020,32(5):95-101.
[11] 刘洋,宫志华,田家磊,等.基于量子遗传算法的雷达组网布站分析 [J].弹道学报,2019,31(4):39-43+67.
[12] 崔玉娟,察豪,田斌.改进的混合蛙跳算法在雷达网部署中的应用 [J].海军工程大学学报,2015,27(1):108-112.
[13] 刘砚菊,胡杨,于洋,等.基于改进粒子群算法的复杂地况下雷达布站优化 [J].火力与指挥控制,2014,39(9):164-168.
[14] LI Z M,CHEN H N,CHU H X,et al. Monitoring Wildfire Using High-resolution Compact X-band Dual-polarization Radar: A Case Study in Southern China [J].Atmospheric Research,2019,225:165-171.
[15] 董晶,陈辉,刘云龙.基于地球曲率的雷达地形遮蔽盲区计算 [J].中国电子科学研究院学报,2021,16(4):408-413.
[16] 陈明福,王超,施军.多站无源雷达作用距离和覆盖范围分析 [J].现代雷达,2020,42(2):7-11+15.
[17] LI H P,FENG D Z,LIU C,et al. Optimal Deployment of Multistatic Radar for Belt Barrier Coverage [J].Wireless Networks,2022,28(5):2213-2235.
[18] MINTEUAN G,PALADE T,PUSCHITA E,et al. Monopulse Secondary Surveillance Radar Coverage-Determinant Factors [J].Sensors,2021,21(12):4198.
[19] 冯克涛,李晓毅,曲晨,等.基于DEM的民航地空VHF通信有效覆盖仿真研究 [J].系统工程与电子技术,2022,44(2):684-695.
[20] 廖玉忠,张自林.基于改进量子粒子群算法的雷达布站优化研究 [J].航天电子对抗,2011,27(2):24-27+43.
[21] 王中杰,李侠,周启明,等.多约束条件的雷达组网系统部署决策问题 [J].火力与指挥控制,2008,33(12):133-136.
[22] 汤国安,李发源,刘学军.数字高程模型教程:第2版 [M].北京:科学出版社,2010.
[23] 徐公国,单甘霖,段修生.基于改进d-Xdraw算法的起伏地形下异构多传感器分簇部署方法 [J].系统工程与电子技术,2019,41(7):1516-1524.
[24] 王豪.大区域多尺度雷达遮蔽角计算关键技术研究与实现 [D].郑州:解放军信息工程大学,2011.
[25] 陈超凡,江晶,李佳炜.一种用于雷达遮蔽分析的DEM数据处理方法 [J].空军预警学院学报,2020,34(1):21-26.
[26] 刘文评,曹博,刘志刚,等.不规则地形对ADS-B地面站信号覆盖影响分析 [J].电光与控制,2016,23(6):84-89.
[27] ZHAI Y,XU M,DIMOPOULOS I S,et al. Quantification of RPE Changes in Choroideremia Using a Photoshop-Based Method [J].Translational Vision Science amp; Technology,2020,9(7):21.
[28] 泮樟胜,叶连宝.浅谈利用PhotoShop精确计算图形面积 [J].绿色科技,2012(8):261-263.
作者简介:刘赓(1985—),男,汉族,四川成都人,硕士研究生,研究方向:情报处理、任务规划;通讯作者:李晓毅(1973—),男,汉族,重庆人,教授,博士,研究方向:雷达对抗、无线光通信。
收稿日期:2022-09-16
基金项目:军内科研项目(KYCQJWJK1703)