摘" 要:基于开普勒第三定律,研究Starlink卫星轨道运行轨迹,分析其轨道运行特征,建立轨道仿真模型,使用高阶的Runge-Kutta方法求解方程,并利用STK对中国东南地区以及中国低纬度地区的Starlink卫星覆盖情况进行分析。仿真结果表明:随着Starlink卫星发射数量的增加,整体覆盖能力稳步提升。最开始1 000颗卫星的覆盖范围在北纬54°至南纬54°之间,中国低纬地区的覆盖程度要比中纬地区低;2 000颗卫星在此范围之间的覆盖达到了100%,3 000颗卫星的覆盖水平明显提高,并且向两极方向延伸,但是一直无法覆盖两极地区。
关键词:星链;轨道特征;覆盖分析;运动仿真
中图分类号:TP391.9" 文献标识码:A" 文章编号:2096-4706(2024)11-0049-05
Starlink Satellite Motion Simulation Analysis
WANG Xiaoyu, WANG Yisu
(North China University of Water Resources and Electric Power, Zhengzhou" 450046, China)
Abstract: Based on the Keplers third law of planetary motion, this paper studies the orbit trajectory of Starlink satellite, analyzes its orbit characteristics, establishes an orbit simulation model, uses the high-order Runge-Kutta method to solve the equation, and uses STK (Satellite Tool Kit) to analyze the coverage situation of Starlink satellite in southeast China and low-latitude areas of China. The simulation results show that the overall coverage capacity is steadily improved with the increase in the number of Starlink satellite launches. The coverage of the first 1 000 satellites is between 54°N and 54°S, and the coverage degree of low-latitude areas in China is lower than that of the mid-latitude areas. The coverage of 2 000 satellites has reached 100% between this range, and the coverage level of 3 000 satellites has increased significantly, and it has extended to the poles, but it has not been able to cover the polar regions.
Keywords: Starlink; orbit characteristic; coverage analysis; motion simulation
0" 引" 言
近20年来,低轨通信卫星数量爆发式增长,低地球轨道(LEO)卫星在年度发射航天器数量占比从57%迅速攀升至97%,年均部署数量提升了2个数量级,直至今日,LEO轨道卫星占比超过83%。卫星互联网巨大的潜在应用效能已经引发政府、军方、商业等多方力量的强烈关注和重视[1]。其中,美国SpaceX的Starlink计划尤为突出:为世界各地的用户提供高速宽带互联网服务,包括了位于不同近地轨道(LEO)和极低地球轨道(VLEO)星座的约12 000颗卫星[2],共计约4.2万颗通信卫星。
目前,随着航天事业的发展,空间任务也在不断增多,采用的新技术新方法也在不断增加,但这些新技术新方法的正确性与可靠性无法验证,并且目前已开展的研究项目大多数都基于常规的卫星和小卫星平台,以微纳卫星为平台开展的仍属于少数。目前,用Starlink卫星的数值仿真的方法,即建立微纳卫星运动的数学模型,通过计算软件进行微纳卫星的轨道和姿态的参数模拟仿真。
本文分析了星链的研究意义和Starlink卫星的运动特性,基于开普勒第三定律等建立了Starlink卫星的运动模型,并利用卫星仿真工具包stk对星链组网进行辅助模拟计算,以验证在误差允许范围内的模型精确性,并进行相关的覆盖分析,为国内后续研究微纳卫星相关的卫星导航、通信和广播、科学研究以及探测任务等提供了有效的参考。
1" 星链(Starlink)系统简介
Starlink计划是SpaceX公司于2015年提出的一个全球互联网项目,通过发射卫星构建网络,以实现提供高速、可靠的互联网连接的目的,该公司已经宣布星链互联网服务已覆盖美国、加拿大、英国、德国、新西兰、澳大利亚等32个国家[3],用户数量超过了100万[4],国际市场进一步扩大,优势愈发明显。庞大的微纳卫星数量以及广泛的覆盖,提供全球范围内的高速互联网接入,改善互联网服务的覆盖范围和质量,同时推动太空经济的发展。建立卫星网络,推动了太空产业的发展,包括卫星制造、发射、运营和相关技术的创新。
由于SpaceX公司只发射了Starlink第一阶段的1 584颗卫星于22个轨道上,故本文仅将已知卫星作为研究对象。其中,卫星以STARLINK-abcd格式命名,ab表示轨道面序号,cd表示某轨道面上的卫星序号[5],以其中5个Starlink卫星为例,Starlink卫星参数如表1所示。
星链是由直径约3米的平板组成,上面安装着通信天线和推进系统,在最初星座层的550 km高度,它们将根据方向呈1°到4°的角度[6]。根据官方给出的Starlink卫星覆盖角度,可在距视轴(天底)最远44.85°的范围提供服务,用户终端与Starlink卫星连线与地面夹角可达到40°仰角[7],如图1所示。
2" Starlink卫星的模型构建与计算
2.1" 真近点角的计算
真近点角f表示轨道六根数之一,对于计算微纳卫星的轨道位置具有极其重要的作用。本文中f表示时刻t卫星的真近点角,此时r表示卫星与地心间的距离,则根据开普勒第二定律有:
(1)
式(1)中,h表示积分常数,表示航天器单位时间内扫过的面积,a表示卫星轨道长半轴,e表示轨道偏心率,μ表示地心引力常数[8]。
此时卫星与地心间的距离r与真近点角f对应关系为:
(2)
式(1)(2)构成了Starlink卫星在其轨道平面上运动的仿真计算模型,本文选择运用四阶Runge-Kutta算法对该微分方程进行求解。
Runge-Kutta是一种可靠且高精度的数值积分方法,相对于低价,能够提供更高的数值精度,且步长可定、结果稳定可靠。利用四阶Runge-Kutta算法,对于该微分方程,建立方程组如下:
(3)
对于式(3)中f的求解公式如下:
(4)
式(4)中的k1,k2,k3,k4求解方程组如下:
(5)
式(5)中,h表示求解步长,Starlink卫星轨道仿真求解的精度可以直接通过仿真步长进行控制,简单易行,便于实验调试。本文取步长h为1,即表示1秒,并对5个不同编号的Starlink卫星的运行速度(角度/秒)进行计算,然后与stk的结果进行对比,对比结果如表2所示。
通过对比分析,并计算误差率,可知在一定的误差允许范围内,本文的四阶Runge-Kutta法具有可行性和可信性。对于存在的误差,本文分析可能由于地球本身是非圆球体摄动、空气阻力、地球磁场环境不同、重力因素影响等原因,造成一定的误差结果。
2.2" Starlink卫星位置关系以及轨迹求解
如图2所示,OXYZ表示地心惯性坐标系,S表示微纳卫星t0时刻的瞬时位置,M表示春分点,N表示轨道升交点,Ω表示升交点赤经,u表示纬度幅角,i表示轨道倾角,作球面三角形SMN [9]。
根据球面三角形公式可得:
(5)
又根据平面三角形公式,可计算出Starlink卫星在OXYZ地心惯性坐标系中X的值:
(6)
用类似的方法,计算出y、z,进而有:
(7)
利用式(5)(6)(7),可计算出在地心惯性坐标系下Starlink卫星的坐标位置,将卫星模拟环境大大简化,可更高效地对Starlink卫星进行分析。
Ωe表示地球自转角速度,λ表示星下点轨迹的经度,δ表示星下点轨迹的纬度,详细计算方法本文不再叙述,进一步可得Starlink卫星星下点轨迹的经纬度:
(8)
式(8)中,λ1表示Starlink卫星处于升轨状态时的经度计算,λ2表示其处于降轨状态时的经度计算。
如图3所示,太阳角β表示地心—太阳方向向量与卫星轨道平面法线n的夹角,α表示卫星轨道平面中会日点与近地点的夹角,相关计算方法本文在此省略,可参考文献[10]。
进一步可计算出地心—太阳方向向量与卫星—地球方向向量夹角的余弦:
(9)
如图4所示,由于地球距离太阳遥远并且Starlink卫星体积微小,故本文将太阳光近似看作平行光线,Starlink卫星近似看作质点,计算时不将Starlink卫星半径考虑在内。此时,d0表示Starlink卫星进入地球阴影时太阳光方向向量与地球向量夹角的临界值,Re表示地球半径,则根据图4几何关系:
(10)
当卫星处于地球阴影部分时:
(10)
3" Starlink卫星覆盖分析
本文根据SpaceX公布的卫星轨道根数,以在官方网站AGI于2023年11月6日导出的Starlink卫星.TLE文件,利用卫星工具包(stk)对Starlink卫星对地面的覆盖分析。本文分别以1 000、2 000、3 000颗Starlink卫星作为研究对象,对仿真结果进行分析和比较。
从图5、6、7全球覆盖分析可以发现,1 000颗Starlink卫星的覆盖范围在北纬54°至南纬54°之间,2 000颗Starlink卫星大部分仍然处于北纬60°至南纬60°之间,但是有极少数的卫星已经逐渐开始向高纬度方向延伸覆盖,3 000颗时,已经有小部分的Starlink卫星继续逐渐向两极地区覆盖,可见Starlink卫星覆盖密度逐渐提高,但是南北两极一直无法覆盖。
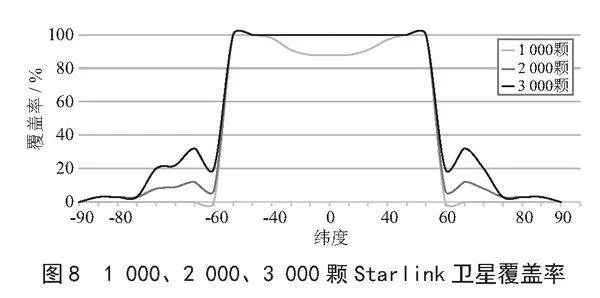
从图8可以分析出不同数量的Starlink卫星对全球地面不同纬度内覆盖时间比例。添加1 000颗Starlink卫星时,在北纬30°~55°和南纬30°~55°附近两个区域覆盖率基本可实现90%以上,但是低纬地区的覆盖水平并不高,在北纬47°~53°和南纬北纬47°~53°之间可实现100%的覆盖率;而当Starlink卫星数量增加到2 000 颗时,在北纬53°直至南纬53°之间覆盖率有明显的提升,已经达到了100%的覆盖率,并且南北纬高纬度地区的覆盖率也有一定的增加;当Starlink卫星数量增加到3 000 颗时,Starlink卫星向两极方向的覆盖逐渐增加,但是仍然无法覆盖到两极。
4" 结" 论
本文基于对Starlink卫星运动研究的需要,获取Starlink卫星的基本参数,分析Starlink卫星的运动特性,基于开普勒第三定律建立Starlink卫星的运动仿真模型,对于求解关键参数真近点角f,本文使用了四阶Runge-Kutta求解微分方程,使得计算机结果更精确,并与stk计算结果比较分析。
其次,本文使用stk,对全球进行了Starlink卫星覆盖分析,寻找覆盖规律,得出结论:Starlink卫星在中纬地区的覆盖能力最强,分别向赤道即低纬地区以及两极即高纬度地区呈递减趋势;当Starlink卫星数量逐渐增加后,卫星对全球的覆盖情况整体上升,但是两极地区一直难以覆盖。
目前,SpaceX公司已经发射了5 300颗卫星,其中4 800颗在正常运行。Starlink卫星计划的诞生以及卫星的发射,无疑为国家的地区安全带来严峻挑战,同时卫星帮助满足实现各类任务需求,产生巨大的经济和社会效益,又进一步加剧全球对低轨太空资源的争夺,发展低轨卫星已经成为重点工程。
2021年中国启动了“星网”项目,中国卫星网络集团和中国卫通合作,联手加入低轨资源争夺战,以更好地保护国家网络安全。国家发改委已经将卫星互联网建设纳入国家“新基建”建设计划,将加大对“虹云工程”“鸿雁星座”两大卫星通信卫星系统的建设力度,加速布局天基互联网系统,加快我国低轨卫星网络和空天地一体化建设。
参考文献:
[1] 王韵涵,李博,刘咏.国外低轨卫星互联网发展最新态势研判 [J].国际太空,2022(3):7-12.
[2] CHAUDHRY A U,YANIKOMEROGLU H. Laser Intersatellite Links in a Starlink Constellation: A Classification and Analysis [J].IEEE Vehicular Technology Magazine,2021,16(2):82.
[3] 孙美玉,彭健,周钰哲.SpaceX发展路径及启示 [J].卫星应用,2022(8):41-43.
[4] JEWETT R. SpaceX Starlink Internet Service Surpasses 1M Subscribers [EB/OL].(2022-12-19).https://www.satellitetoday.com/connectivity/2022/12/19/spacex-starlink-internet-service-surpasses-1m-subscribers/.
[5] 李元龙,李志强.Starlink星座通信建模仿真分析 [J].指挥控制与仿真,2023,45(4):118-126.
[6] MCDOWELL J C. The Low Earth Orbit Satellite Population and Impacts of the SpaceX Starlink Constellation [J/OL].arXiv:2003.07446 [astro-ph.IM].(2020-03-16).https://arxiv.org/abs/2003.07446v2.
[7] 王迪,骆盛,毛锦,等.Starlink卫星系统技术概要 [J].航天电子对抗,2020,36(5):51-56.
[8] 李运泽,宁献文,王晓明,等.纳卫星轨道热环境仿真分析 [J].系统仿真学报,2007(14):3166-3168+3175.
[9] 张雅声,徐艳丽,杨庆.航天器轨道理论与应用 [M].北京:清华大学出版社,2020.
[10] 闵桂荣.卫星热控制技术 [M].北京:宇航出版社,1991.
作者简介:王小雨(2003—),女,汉族,河南平顶山人,本科在读,研究方向:系统仿真。
收稿日期:2024-03-08