



摘" 要:为了解决传统Floyd算法生成路径中出现的结点遗漏问题,提出三种构造路径的方法对Floyd算法进行改进。首先,使用代数方法推演了三种方法构造路径的过程,分别证明了三种方法的正确性;然后,证明了基于“递归法+后继顶点法”组合方法在增减序列存在“zz”“zjz”或“jzj”其中一种子串的条件下,Floyd算法生成的路径中存在结点遗漏的情况,解答了出现结点遗漏的原因;最后,对Floyd算法的正确编写方法给出建议。实验结果表明,基于Floyd算法改进的三种构造路径的方法能够生成不遗漏结点的最短路径。
关键词:Floyd算法;生成路径;结点遗漏;递归法;后继顶点法
中图分类号:TP312" 文献标识码:A" 文章编号:2096-4706(2024)11-0031-09
Research on the Shortest Path of the Improved Floyd Algorithm Integrating Path Generation Process
FAN Nisheng, HU Yibo, KE Jinhong, WANG Jiaqi, XIA Xiaoyun
(Jiaxing University, Jiaxing" 314001, China)
Abstract: In order to solve the problem of missing nodes in the generation path of traditional Floyd algorithm, three methods of path construction are proposed to improve Floyd algorithm. Firstly, the process of constructing the path by three methods is deduced by algebraic method, and the correctness of the three methods is proved respectively. In the next section, it is proved that node omission exists in the path generated by Floyd algorithm based on the combination method of “recursion method + successor vertex method” under the condition that Increase/decrease sequence has one of the seed strings of “zz”“zjz”or“jzj”, and the reason of node omission is explained. Finally, the author gives some suggestions on how to write Floyd algorithm correctly. The experimental results show that the three methods of path construction improved by Floyd algorithm can generate the shortest path without missing nodes.
Keywords: Floyd algorithm; generation path; node omission; recursion method; successor vertex method
0" 引" 言
最短路径问题是图论问题中非常重要的一个分支[1]。Floyd算法是求解最短路径问题的经典算法之一[2],它是一种应用于求解给定的加权图中各个顶点之间的最短距离,并将求解结果保存入二维数组L[][]的算法[3]。同时,也可以构造一个同型的二维数组PATH[][]。
在传统的Floyd算法中,此数组的元素PATH[i][j]为穷举结点i、j的断点[4],因此常常通过该数组构造出从起点astart到终点aend之间的最短路径。但本文的研究发现,某些由Floyd算法构造的路径存在中间一些结点遗漏的情况。结点遗漏是指,在最短路径算法构造的结点顺序表中,存在相邻两个元素,它们对应的结点为图中两个不邻接的结点。
本文研究表明,点的遗漏的原因不仅与二维数组PATH[][]的赋值方式有关,也与构造路径的算法有关。若数组的元素PATH[i][j]仅为穷举结点i、j的断点且使用了对应的构造路径的算法,则确实能得到完整路径,反之如果用错了构造路径的算法,则可能会存在结点遗漏[5],将造成算法计算出实际情况中不存在的路线的问题。因此,生成的路径中出现结点遗漏的问题亟待研究。
1" 相关工作
最近三年来的研究表明,Floyd算法的应用领域广泛,可以独立解决或辅助解决许多问题,例如:路线规划[3,6-11]、避障避险[12-14]、方案优化[15]、路网布局[16]、乱序图像拼接[17]等。路线规划属于Floyd算法的第一类应用。刘芳等[6]提出了简单因素下的多目标整体最优路线规划,其中,借助Floyd算法计算景区各景点之间的最短距离。张帝等[7]提出基于Floyd算法的有毒气体泄漏的人员疏散路径规划方法,可为化工园区内大多数建筑提供方案,但未考虑建筑等障碍物对有毒气体扩散的影响。惠庆华等[8]为了解决疫情防控中存在的物资配送方案漏洞,利用Floyd算法,建立了经济快速且风险度最低的运输方案。在各种具体的研究项目里,还有一部分使用了其他方法对Floyd算法改善,使之拥有更强大的计算性能,或能够处理更加特殊的需求。主国娜等[3]提出了用模拟退火算法迭代优化的方法对Floyd算法进行改进,也应用于农村应急物流配送路径的优化研究。Yang等[9]实现了一种基于多层负载均衡策略的并行Floyd算法,在计算过程中使用动态负载平衡技术,根据不同节点的计算量进行动态调整,在大规模图上表现出很好的加速效果。袁梦婷等[10]通过量化不确定因素的方式提高Floyd算法的兼容性,提高了生鲜农产品冷链运输过程的经济效益。Bożejko等[11]提出了一种动态规划的思想,对于加速图处理、网络分析等领域具有重要的意义。
解决类图论问题是Floyd算法的第二类应用。邵丽丽[12]针对危险区域为多边形或圆盘约束的无人机巡航路径问题,提出了利用Floyd算法,改良圈算法,遗传算法来综合求解的方法。龚鹏等[13]和高九州等[14]把扩展子结点与Floyd算法结合起来,对路径进行平滑处理,不仅减少了航线转角数量,也使得转角相对平缓,改进算法能有效地避障且效率高。赵立杰等[17]提出了一种基于Floyd算法的多图像拼接方法,解决了视野受限、多图乱序情况下显微图像的拼接问题。Maady等[18]设计了一种新的节点映射方法应用于基于双重压缩数据结构的社交网络加权图的Floyd算法,以此加速社交网络加权图的计算速度。一些优化类问题把利润最大或成本最小作为求解目标,Floyd算法给这些问题提供了思路。张雨筱等[15]在Floyd算法中引入0-1变量,分析不同情况下的供应链网络建立及最短路径优化问题,对企业实现利益、效率最大化有重要意义。裴玉龙等[16]针对传统方法无法同时考虑现有路网与新建路网的缺陷,建立了探寻重要节点间需求度最大的路径的改进Floyd算法,并引入建设阻抗系数,提出了基于综合交通理念的主要干线公路网布局方法。
曾有不少研究提出对Floyd算法的改进方法,但改进的方向以提升算法的性能为主,并没有对构造路径的过程进行剖析。Nova等[19]提出了一种新的自组织网络(vanet)安全和sybil攻击检测框架,并在定位K-means算法的簇头过程中使用Floyd-Warshall算法,优于现有模型。Wang等[20]通过引入Floyd算法和多目标优化函数,提高了路径规划的收敛速度和全局最优解概率,从而更加高效地实现单源最短路径计算。李金泽等[21]提出基于Floyd改进算法的控制策略,其依据系统的实时变化对权值进行动态调整,结果表明,该改进使Floyd在各项指标上显著优于其他算法,但当实验数组达到一定上限时,该改进的效果则不显著。魏玉华等[22]研究了Floyd算法的位置矩阵由一个2维的位置矩阵,推广到两个4维矩阵,分别表示节点的横纵坐标,使得最短路径的计算更为便捷。近三年来,部分文献[4,23]中的代码仍存在“构造路径的算法使用错误”的问题;而也有一些文献采用了正确的代码,但未给出其改进的原因。因此,本文着力于解决PATH数组的赋值方法的问题和构造路径算法的使用方法的问题。对目前已知的Floyd算法三种构造路径的方法,分别是递归法、后继顶点法、前驱顶点法,推导演示每种方法构造路径的过程,对三种方法的正确性分别证明。然后剖析生成的路径中出现结点的遗漏的情况的原因,最后对Floyd算法的正确编写方法给出建议。
2" 概念设计与代数表示
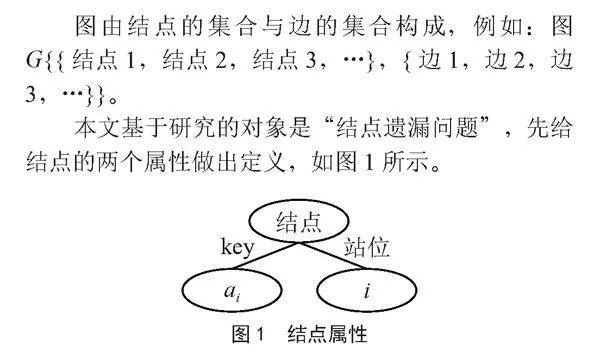
图由结点的集合与边的集合构成,例如:图G{{结点1,结点2,结点3,…},{边1,边2,边3,…}}。
本文基于研究的对象是“结点遗漏问题”,先给结点的两个属性做出定义,如图1所示。
2.1" key属性
第一个属性是key,意为关键字。关键字是Floyd算法的三层循环里每层循环都遍历的值。在Floyd算法中,最外层循环值又称为“断点”,它是将两个端点通过已构造的路径连接在一起的桥梁。一般把最外层循环值赋值给k,即k就是“断点”。因此,本文所述路线中的结点的关键字值key的大小,决定了这些结点在Floyd算法中作为“断点”的先后顺序。
2.1.1" key值的唯一性
任意两个结点关键字之间不相等。当i ≠ j时,不存在ai = aj的情况。
2.1.2" key值的非零性
受PATH矩阵的主对角线和邻接结点之间的值设为0的影响,要求最外层循环值k不能为零,所以本文应设各结点的key值不为零。
2.2" 站位问题
第二个属性是当G为“一个边数比结点数少1的连通图”的情况下讨论的。这个属性是“站位”,站位的本质是数组元素的下标,在数组的范畴里,下标按着序排,所以站位应当是从小到大顺序排列。也可以说,站位问题本质是排列问题。与数组下标从0开始有所区别,站位从第1位开始。
2.3" 递增递减问题
对于同一组数的不同排列,站位问题会影响到这个排列中数的大小的递增递减问题。例如序列4,5,3,2,1中数字4的站位是第1位,递增递减序列为“增减减减”,序列5,4,3,2,1中数字4的站位是第2位,递增递减序列为“减减减减”,两者比较,递增递减序列不同。但不同的序列不代表递增递减序列一定不同,又如4,5,3,2,1与3,5,4,2,1,两者比较,递增递减序列相同。研究本课题的核心问题正是基于这一递增递减概念。
2.4" 代数表示
为了简化研究过程,本文把研究对象设定为原图的具有一定特性的子图,即一个边数比结点数少1的连通图。具体描述如下:设图G中有n个结点,序列a中存放了这n个结点的key属性,用集合表示为{a1,a2,a3,…,an},(n≥,n ∈ N∗)。
设由图G中r个结点的key属性组成的互异数数列为A: am,am+1,…,am+r-1 (r ∈ {3,4},1≤m≤n - r + 1),并且,对于i ∈ [0,r - 2],am+i与am+i+1邻接,am+i与am+i+1的大小关系如下:
记这r个结点的递增递减序列为ZJ序列,在计算机程序中,ZJ序列初始化为一个有r - 1个元素的“char类型”数组。对于i ∈ [0,r - 2],若am+i<am+i+1,则ZJ[i] =“z”;若am+i>am+i+1,则ZJ[i] =“j”。
图G中其他的任意的结点与结点之间的邻接关系、大小关系不对本研究产生影响,因此均忽略不讨论。
在下文的需引出路径的各个描述语句中,也使用结点的key属性指代结点。本文还假设经过Floyd算法的计算后,路线am→am+1→…→am+r-1始终是am至am+r-1的最短路线。根据站位“理论”,在这段路线中,am的站位是第1位,am+1的站位是第2位,…,am+r-1的站位是第r位。
2.5" 数列的ZJ序列的特点
2.5.1" ZJ序列的列举
由本文第2.4节可知,r = 3时,对于大小关系未知,但排列顺序已知的互异数数列am,am+1,am+2,其ZJ序列有4种可能的情况,即:“zz”“zj”“jz”“jj”。
r = 4时,对于大小关系未知,但排列顺序已知的互异数数列am,am+1,am+2,am+3,其ZJ序列有8种可能的情况,即:“zzz”“zzj”“zjz”“zjj”“jzz”“jzj”“jjz”“jjj”。其中,字符串“zzz”“zzj”“jzz”都含有子串“zz”,字符串“zjj”“jjz”“jjj”都含有子串“jj”,字符串“zjz”含有子串“zjz”,字符串“jzj”含有子串“jzj”。
2.5.2" ZJ序列的递推式
结合本文第2.3、2.4节,可知ZJ序列为一个仅由字母“z”“j”组成的字符串。这说明,若ZJs为任意一个长度等于s的ZJ序列,那么ZJs、ZJs+1关系为:
ZJs+1 = “z”+ ZJs或ZJs+1 =“j”+ ZJs
可以看出,对于满足上式的两个ZJ序列ZJs、ZJs+1,ZJs是ZJs+1的子串。
结合第2.5.1、2.5.2节的结论递推,可知,r≥4时,数列的ZJ序列的特点为:对于∀ZJs (s≥3),∃x∈{“zz”“jj”“zjz”“jzj”},使得x是ZJs的子串。
2.6" 结点遗漏证明问题的简化
根据本文第2.4节,设数列A的ZJ序列为ZJr,可再设A [i:i + t - 1]为从数列A中截取连续的t个数作为一个新数列,其中m≤i≤m + r - t,其ZJ序列为ZJt,则ZJt是ZJr的子串。
经过推导可知,使用Floyd算法的计算后,如果A [i:i + t - 1]段所得路径与真实的情况相比较,存在结点遗漏,那么整个A段所得路径与真实的情况相比较,也存在结点遗漏。
综上所述,只需证明,r = 3或r = 4时,且ZJ为“zz”“jj”“zjz”“jzj”其中一种情况的条件下,Floyd算法生成的路径中存在结点遗漏;对于r>4的情况,由于数列的ZJ序列必然存在上述子串,而子串对应的数列又由原数列截取而来,所以,也会存在结点遗漏。
3" 公式与证明
目前Floyd算法有三种构造路径的方法,分别是递归法、后继顶点法、前驱顶点法。它们构造路径的方法不同,但过程是统一的,总结如下:首先初始化连通图G的加权邻接矩阵、PATH矩阵。对于加权邻接矩阵,主对角线的值设为0,邻接结点之间的值设为边的权重;对于PATH矩阵,主对角线和邻接结点之间的值设为0;两个矩阵中的其余情况均设为无穷值INF。接着使用Floyd算法求解G的PATH矩阵,此为“步骤一”;再调用PATH矩阵和构造路径的公式,生成路径,并将求解结果保存入数组R[],此为“步骤二”。具体算法流程如图2所示。
令r = 4,则根据2.4节,设定的研究对象为以下所示的子图:
该子图中任意的结点与结点之间的大小关系不对本研究产生影响,因此忽略不讨论。令am+4和am+3邻接,此时1≤m≤n - 4,结点数变为5个,即r = 5。忽略am+4和am+3之间的大小关系。假设经过Floyd算法的计算后,路径am→am+1→am+2→am+3→am+4始终是am至am+4的最短路径。根据2.2节的站位理论,在这段路径中,am的站位是第1位,am+1的站位是第2位,…,am+4的站位是第5位。
3.1" 递归法
递归法通过递归端点与断点之间所有的结点构造整段路径,其“步骤一”“步骤二”的公式分别为式(1)(2):
(1)
(2)
式中,Rmiddle = PATH[Rstart][Rend],对于i ∈ [0,r - 1],保证R[i] ≠ 0。
3.1.1" 套用式(1)完成步骤一
本节中,子图的ZJ序列是不确定的。使用递归法构造该PATH矩阵,依据不同的ZJ序列将得出不同的结果。但由于不同的PATH矩阵构造结果,不影响递归法的步骤二构造路径的过程。所以,受篇幅所限,递归法的步骤一的过程省去。本文将在下文第4节具体阐述此处省去的内容。
3.1.2" 套用式(2)完成步骤二
递归法构造路径过程阐述如下:
1)把R[0]作为递归函数的起点参数Rstart,把R[r - 1]作为递归函数的终点参数Rend。
2)若递归函数的起点、终点既不邻接也不是同一结点,则从PATH矩阵中索引出它们之间的断点。否则,跳过第3)、4)步骤。
3)把当前起点作为下一层递归函数的起点,把当前断点作为下一层递归函数的终点,并执行第2)步操作。
4)把当前断点作为下一层递归函数的起点,把当前终点作为下一层递归函数的终点,并执行第2)步操作。
5)返回上一层递归。
具体算法流程如图3所示。
综上所述:路径中的所有结点都能被递归到,递归完成的路径则插入R数组中。最终R数组内key值排列的顺序就是路径结点的顺序。最终得路径为:am→am+1→am+2→am+3→am+4,结果与真实的情况相符合,经检验可知方法正确。
3.2" 后继顶点法
后继顶点法通过顺序连接各后继顶点构造整段路径,其“步骤一”“步骤二”的公式分别为式(3)(4):
(3)
(4)
式中,R[0] = Rstart,R[1] = PATH [R[0]][Rend],…,R[r - 2] = PATH [R[r - 3]][Rend] ≠ 0。
3.2.1" 套用式(3)完成步骤一
1)讨论PATH[am][am+3]的值。
如果在k = am+2时形成通路,PATH[am][am+3] = PATH[am][am+2];如果在k = am+1时形成通路,由于PATH[am][am+1] = 0,所以得am+1,即PATH[am][am+3] = am+1 = PATH[am][am+2]。
2)讨论PATH[am][am+4]的值。
如果在k = am+1时形成通路,PATH[am][am+4] = am+1 = PATH[am][am+2];如果在k = am+2时形成通路,PATH[am][am+4] = PATH[am][am+2];如果在k = am+3时形成通路,PATH[am][am+4] = PATH[am][am+3] = PATH[am][am+2]。
3)讨论PATH[am+1][am+4]的值。
如果在k = am+2时形成通路,PATH[am+1][am+4] = am+2 = PATH[am+1][am+3];如果在k = am+3时形成通路,PATH[am+1][am+4] = PATH[am+1][am+3]。
综上所述:PATH[am][am+3] = PATH[am][am+2],PATH
[am][am+4] = PATH[am][am+2],PATH[am+1][am+4] = PATH[am+1][am+3]。可得如下所示的PATH矩阵:
3.2.2" 套用式(4)完成步骤二
首先推导R[]列表的元素:
R[0] = Rstart = am,R[1] = PATH[R[0]][Rend] = PATH[am][am+4] = PATH[am][am+2],R[2] = PATH[R[1]][Rend] = PATH[am+1][am+4] = PATH[am+1][am+3],…,R[i] = PATH[R[i-1]][Rend] = PATH[am+i-1][am+i+1],…,[R[r-1] = Rend = am+4。
综上所述:R数组的推导结果收敛为:
R[] = {Rstart,PATH[am][am+2],PATH[am+1][am+3],…,PATH[am+i-1][am+i-1],…,Rend}。最终得路径为:am→
am+1→am+2→am+3→am+4,结果与真实的情况相符合,经检验可知方法正确。
3.3" 前驱顶点法
前驱顶点法通过顺序连接各前驱顶点构造整段路径,其“步骤一”“步骤二”的公式分别为式(5)(6)为:
(5)
(6)
式中,R[r-1] = Rend,R[r-2] = PATH[Rstart][R[r-1]],对于i ∈ [0,r-1],保证R[i] ≠ 0。
3.3.1" 套用式(5)完成步骤一
受篇幅所限,本文省略前驱顶点法构造PATH矩阵的过程,直接给出PATH矩阵构造结果:
3.3.2" 套用式(6)完成步骤二
首先推导R[]列表的元素:
R[r-1] = Rend = am+4,R[r-2] = PATH[Rstart][R[r-1]] = PATH[am][am+r-1] = PATH[am+r-3][am+r-1],R[r-3] = PATH[Rstart][R[r-2]] = PATH[am][am+r-2] = PATH[am+r-4][am+r-2],…,R[i] = PATH[Rstart][R[i+1]] = PATH[am+i-1][am+i+1],…,R[0] = Rstart = am。
综上所述:R数组的推导结果收敛为R[] = {Rstart,…,PATH[am+i-1][am+i+1],…,PATH[am+r-4][am+r-2],PATH[am+r-3][am+r-1],Rend}。最终得路径为:am→am+1→am+2→am+3→am+4,结果与真实的情况相符合,经检验可知方法正确。
4" “递归+后继”结点遗漏证明
“递归+后继”即步骤一使用递归法构造PATH矩阵,步骤二使用后继顶点法生成路径。本节把结点遗漏的基本条件分为三种,分别为ZJ序列中存在“zz”“zjz”或“jzj”其中一种子串。基于这三种不同的基本条件,分别剖析“递归+后继”方法构造路径的过程,证明其结果中存在结点遗漏,总结出现结点的遗漏的情况的原因,从而解答“生成的路径中出现结点的遗漏的情况”的问题。
4.1" 在ZJ序列中存在子串“zz”
令r = 3,则根据2.4节,设定的研究对象为如下所示的子图:
am--am+1--am+2
且,使得am<am+1且am+1<am+2。
4.1.1" 情况1
令am+3和am+1邻接,此时1≤m≤n-3。忽略am+3和am+2之间的大小关系。假设经过Floyd算法计算,路径为am→am+1→am+2→am+3始终是am至am+3的最短路径。根据2.2节的站位理论,在这段路径中,am的站位是第1位,am+1的站位是第2位,…,am+3的站位是第4位。构造PATH矩阵流程如图4所示。
首先am、am+1、am+2这三个结点作为断点的先后顺序,由它们的key属性之间的大小关系决定。当k<am+1(包括等于am)时,由于k在上述路径中不能作为断点,所以在这些循环中,不会对该子图的PATH矩阵产生变化;当k = am+1时,因为am与am+3邻接,am+1与am+2邻接,am与am+2之间的通路形成,PATH[am][am+2] = am+1;当k = am+2时,由于am与am+2之间的路径已经构造,所以,此时,am与am+3之间的,am+2作为断点的,通路形成,PATH[am][am+3] = am+2;又因为am+1与am+2邻接,am+2与am+3邻接,am+1与am+3之间的通路也形成,PATH[am+1][am+3] = am+2;当k = am+3时,由于am+3在上述路径中不能作为断点,所以在这轮循环中,不会对该子图的PATH矩阵产生变化。可得如下所示的PATH矩阵:
再构造am与am+3的路径。根据式(4),得路径为:am→am+2→am+3。
4.1.2" 情况2
令am-1和am邻接,此时2≤m≤n-2。忽略am-1和am之间的大小关系。假设经过Floyd算法计算,路径为:am-1→am→am+1→am+2始终是am-1至am+2的最短路径。之后,构造的PATH矩阵的过程与4.1.1节类似,受篇幅所限,本文直接给出PATH矩阵构造结果:
再构造am-1至am+2的路径。根据式(4),得路径为:am-1→am+1→am+2。
综上所述,在ZJ序列中存在子串“zz”时,所得路径与真实的情况相比较,均存在结点遗漏。所以,在ZJ序列中存在子串“zz”能作为“递归+后继”结点遗漏的基本条件之一。
4.2" 在ZJ序列中存在子串“zjz”
令r = 4,则根据2.4节,设定的研究对象为如下所示的子图:
am--am+1--am+2--am+3
且,使得am<am+1,am+1>am+2,am+2<am+3。
4.2.1" 情况1
令am+4和am+3邻接,此时1≤m≤n-4。忽略am+4和am+3之间的大小关系。假设经过Floyd算法计算,路径为:am→am+1→am+2→am+3→am+4始终是am至am+4的最短路径。之后,构造的PATH矩阵的过程与4.1.1节类似,受篇幅所限,本文直接给出算法流程,如图5所示。
其中,am+1与am+3之间的大小关系将影响对PATH[am][am+4]的赋值。若am+1>am+3,当k = am+3时,am至am+3之间的路径未构造,所以不能在am与am+4之间形成通路,当k = am+1时,am与am+4之间的am+1作为断点,通路形成PATH[am][am+4] = am+1;反之,若am+1<am+3,PATH[am][am+4] = am+3。可得PATH矩阵:
其中:
再构造am至am+4的路径。根据式(4)可得,若am+1>am+3,路径为am→am+1→am+2→am+3→am+4;若am+1<am+3,路径为am→am+3→am+4。
4.2.2" 情况2
令am-1和am邻接,此时2≤m≤n-3。忽略am-1和am之间的大小关系。假设经过Floyd算法计算,路径为:am-1→am→am+1→am+2→am+3。
始终是am-1至am+3的最短路径。之后,构造的PATH矩阵的过程与4.1.1节类似,PATH矩阵构造结果:
再构造am-1至am+3的路径。根据式(4),得路径为:am-1→am+1→am+2→am+3。
综上所述,在ZJ序列中存在子串“zjz”时,所得路径与真实的情况相比较,均存在结点遗漏。所以,在ZJ序列中存在子串“zjz”能作为“递归+后继”结点遗漏的基本条件之一。
4.3" 在ZJ序列中存在子串“jzj”
令r = 4,则根据2.4节,设定的研究对象为如下所示的子图:
且,使得am>am+1,am+1<am+2,am+2→am+3。
4.3.1" 情况1
令am+4和am+3邻接,此时1≤m≤n-4。忽略am+4和am+3之间的大小关系。假设经过Floyd算法计算,路径为:am→am+1→am+2→am+3→am+4。
始终是am至am+4的最短路径。之后,构造的PATH矩阵的过程与4.1.1节类似,PATH矩阵构造结果:
再构造am至am+4的路径。根据式(4),得路径为:am→am+2→am+3→am+4。
4.3.2" 情况2
令am-1和am邻接,此时2≤m≤n-3。忽略am-1和am之间的大小关系。假设经过Floyd算法计算,路径为:am-1→am→am+1→am+2→am+3。
始终是am-1至am+3的最短路径。之后,构造的PATH矩阵的过程与4.2.1节类似,PATH矩阵构造结果:
其中:
再构造am-1至am+3的路径。根据式(4),可得,若am>am+2,得路径为:am-1→am→am+2→am+3;若am<am+2,得路径为:am-1→am+2→am+3。
综上所述,在ZJ序列中存在子串“jzj”时,所得路径与真实的情况相比较,均存在结点遗漏。所以,在ZJ序列中存在子串“jzj”能作为“递归+后继”结点遗漏的基本条件之一。
4.4" 小结与分析
“递归+后继”生成的路径中存在结点的遗漏的原因:在一条真实路径的ZJ序列中,存在“zz”“zjz”或“jzj”其中至少一种子串。但存在子串只是产生错误时呈现在表面的现象,究其本质,“递归法”“后继顶点法”这两个不同方法构造PATH矩阵和使用PATH矩阵的逻辑是不一样的,这使得混用它们成为引起结点遗漏的表面现象。
5" Floyd算法正确编写方法建议
5.1" 其他方法组合的结点遗漏
本文至此已展示了“递归法+递归法”“后继顶点法+后继顶点法”“前驱顶点法+前驱顶点法”“递归法+后继顶点法”共4种方法组合。若递归法、后继顶点法、前驱顶点法两两组合,共可组合的方法组合数为9种。受篇幅所限,在此无法给出其余5种的正确性证明或路径结点遗漏证明。表1则总结了9种方法组合的结点遗漏的情况。
5.2" Floyd算法正确编写方法建议
若步骤一使用了递归法,即式(1),那么步骤二只能使用式(2),不能使用式(4)或式(6)。
若步骤一使用了后继顶点法,即式(3),那么步骤二只能使用式(2)或式(4),不能使用式(6)。
若步骤一使用了前驱顶点法,即式(5),那么步骤二只能使用式(2)或式(6),不能使用式(4)。
6" 实验验证与软件实现
6.1" 生成最短路径实验
6.1.1" 实验设计
本节用数据实验验证理论推导部分的正确性。
设一个数组N[5] = {1,2,3,4,5},使用C语言程序计算得数组N的全排列,排列种数为5! = 120种。对于i ∈ [1,120],设第i种排列为{n[i][1],n[i][2],n[i][3],n[i][4],n[i][5]},记为数组n[i],数n[i][j](1≤j≤5)看作结点的key,且结点n[i][j]与n[i][j+1]之间都存在无向且权重为有限自然整数的边ej(1≤j≤4),不存在其他边,这样构造出一个含有5个结点和4条边的连通图Gi;设第i种排列中数n[i][v]与n[i][v+1]之间的增减情况为{ZJ[i][v]}(1≤j≤4),记为数组ZJ[i]。
6.1.2" 实验操作
首先初始化连通图Gi的加权邻接矩阵、PATH矩阵。分别使用改进前的和改进后的Floyd算法求解Gi的PATH矩阵,此为“步骤一”;再调用PATH矩阵和构造路径的公式,生成路径,此为“步骤二”。在本课题实验中,具体为生成结点n[i][1]与n[i][5]之间生成的路径,记为数组R[]。
6.1.3" 实验结果
1)使用错误的Floyd算法编写方法。四种错误的编写方法已在上文表1中给出。实验结果表明:使用F1编号方法时,只要ZJ序列中存在“zz”“zjz”或“jzj”其中一种子串,就必然在构造路径的结果中存在结点遗漏;使用F2编号方法时,只要ZJ序列中存在“jj”“zjz”或“jzj”其中一种子串,就必然在构造路径的结果中存在结点遗漏;使用F3、F4编号方法时,只要ZJ序列长度大于等于3,就必然在构造路径的结果中存在结点遗漏。
2)使用正确的Floyd算法编写方法。实验结果表明,使用T1至T5编号方法时,都能够生成不遗漏结点的最短路径。
6.2" 软件实现
6.2.1" 软件简介
Floyd算法的简洁性使其得到广泛应用,因此,本项目开发了一种融合路径生成过程的改进Floyd算法的最短路径问题求解软件,来演示Floyd算法。该软件由Python语言开发,带有生成PATH矩阵、生成路径、结点遗漏检测等功能,界面友好,为解答生成的路径中可能存在结点的遗漏的问题提供了一个简单实用的平台。
6.2.2" 软件解决的问题与创新点
软件在使用Floyd算法的基础上,对PATH矩阵的计算过程使用的方法进行分类与改进,分类出了递归法、前驱顶点法和后继顶点法共三种方法。
软件创新点在于能够辨别使用方法不当的问题。具体如下:首先,软件功能分别基于本文第3节的“步骤一”“步骤二”理论;其次,为了提示软件使用者的使用方法不当的问题,软件设置了相应的警告文字。
当辨别出软件使用者混乱使用上述三种方法来分别进行“步骤一”“步骤二”时,软件立刻在Warning模块给出警告。通过在软件内部生成文字提示,软件解决了Floyd算法使用者,组合使用上述三种方法时,使用了错误组合,形成了错误方法,遗漏了部分结点,生成了错误路径的问题。软件使用者通过在软件中多次试验比较,能总结出“步骤一”“步骤二”使用哪两个方法组合是正确的,哪些是会被警告的。软件帮助软件使用者学习快速而又精确地求出带权无向图的最短路径,其界面如图6所示。
7" 结" 论
本文重点给出了使用Floyd算法生成路径过程中的三条“步骤一”公式和三条“步骤二”公式。一方面,回答了PATH数组的赋值方法的问题;另一方面,回答了构造路径算法的使用方法的问题。
本文使用代数方法,既证明了递归法、后继顶点法、前驱顶点法这三种方法的正确性;也证明了基于“递归法+后继顶点法”组合方法时,生成的路径中确实存在结点遗漏的情况;本文提出的Floyd算法的编写方法的建议,对正确使用Floyd算法构造路径具有意义。
在实际应用方面,基于Floyd算法的最短路径求解过程开发了一个简单实用的平台,因其带有生成PATH矩阵、生成路径、结点遗漏检测等功能,可以作为众多Floyd算法研究的参考之一,适合在最短路径教学相关的领域内推广。
参考文献:
[1] 覃柯棚.经典的最短路径算法及实现 [J].中国新通信,2019,21(19):137-139.
[2] KLEENE S C. Representation of Events in Nerve Nets and Finite Automata [EB/OL].[2023-09-06].https://www.degruyter.com/document/doi/10.1515/9781400882618-002/html.
[3] 主国娜,唐小平.基于模拟退火法和Floyd优化算法的农村应急物流配送路径研究[J].软件工程,2022,25(12):9-12+8.
[4] 贺军忠.最短路径问题Floyd算法的改进 [J].兰州文理学院学报:自然科学版,2019,33(5):27-30.
[5] 司守奎,孙兆亮.数学建模算法与应用第2版 [M].北京:国防工业出版社,2017.
[6] 刘芳,李思凡,张超平.基于Floyd算法的景区游历路线规划问题 [J].农村经济与科技,2021,32(3):83-84+126.
[7] 张帝,毛占利,龚美玲,等.基于Floyd的化工园区毒气泄漏人员疏散路径规划 [J].消防科学与技术,2021,40(10):1475-1478.
[8] 惠庆华,张恒运,唐晨洋,等.基于Floyd算法和线性规划的疫情防控物资配送方案[J].青海大学学报,2022,40(4):76-81+87.
[9] YANG J. Application of Floyd algorithm in the design of a coastal Tourism Route Optimization System [J].Journal of Coastal Research,2020,106(SI):668-671.
[10] 袁梦婷,张雨洁.基于改进Floyd算法的生鲜农产品冷链运输路径优化 [J].物流工程与管理,2023,45(2):50-52+49.
[11] BOŻEJKO W,RUDY J,IDZIKOWSKI R. Parallel Computing for the Non-permutation Flow Shop Scheduling Problem with Time Couplings Using Floyd-Warshall Algorithm [EB/OL].[2023-09-06].https://springer.longhoe.net/chapter/10.1007/978-3-030-67063-4_1.
[12] 邵丽丽.有危险区域约束的无人机巡航路径研究 [J].计算机应用与软件,2012,29(9):271-273.
[13] 龚鹏,李文博,马庆升,等.基于改进A*算法的无人车路径规划研究 [J].组合机床与自动化加工技术,2023,589(3):17-20+24.
[14] 高九州,徐威峰,张立辉,等.基于改进A*算法的无人机避障航线规划 [J].现代电子技术,2023,46(8):181-186.
[15] 张雨筱,南卓里,赵淑萍,等.供应链网络建立与最短路径优化问题研究 [J].现代工业经济和信息化,2021,11(11):196-197+223.
[16] 裴玉龙,宇文翀,刘静,等.基于综合交通理念的主要干线公路网布局方法 [J].吉林大学学报:工学版,2023,53(11):3078-3087.
[17] 赵立杰,张桂硕,邹世达,等.基于Floyd算法的活性污泥显微图像的多图像拼接 [J].激光与光电子学进展,2022,59(22):122-129.
[18] MAADY M N P,SYAHDA T S N,RIZQI A F,et al. On using Floyd-Warshall under uncertainty for Influence Maximization in Instagram social network:A case study of Indonesian FnB unicorn company [J].Procedia Computer Science,2024,234:164-171.
[19] NOVA K,UMAAMAHESHVARI A,JACOB S S,et al. Floyd–Warshalls algorithm and modified advanced encryption standard for secured communication in VANET [J].Measurement:Sensors,2023,27:100796.
[20] WANG L N,WANG H J,YANG X,et al. Research on smooth path planning method based on improved ant colony algorithm optimized by Floyd algorithm [EB/OL].[2023-09-06].https://www.frontiersin.org/articles/10.3389/fnbot.2022.955179/full.
[21] 李金泽,武文豪,李开航.基于改进Floyd算法的网络舆情监测 [J].计算机与现代化,2021(5):73-77+82.
[22] 魏玉华,谢小军,薛申芳.Floyd算法的推广 [J].贵阳学院学报:自然科学版,2022,17(4):115-119.
[23] 蔡佳成,白克强,李旭春,等.基于JPS改进的移动机器人路径规划算法 [J].计算机应用研究,2022,39(7):1985-1991.
作者简介:范倪圣(2002—),男,汉族,江苏南通人,本科在读,研究方向:数学建模;通讯作者:夏小云(1982—),男,汉族,江西南昌人,副教授,博士,研究方向:计算智能、调度优化等。
收稿日期:2023-09-25
基金项目:2022年度嘉兴学院大学生研究训练(SRT)计划项目(8517221274)