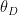

摘 要:对如何提升电磁侦察仿真模型逼真度进行了模型校验方法的研究,针对传统电磁侦察模型与实际效能相差较大等问题,参考数字孪生和黑白盒模型构建的思路,提出基于数据对模型进行逆向校验的方法,从侦察距离、测向和截获数据率3个方面提出了校验算法,并基于仿真数据对校验算法进行验证,仿真案例表明文章提出的方法可以解决电磁侦察模型中3个效能计算结果的逼真度问题,对构建高置信度的电磁侦察模型可起到指导作用,同时该方法可以为其他电磁领域模型的校验提供方法参考。
关键词:模型校验;电磁侦察;模型数据
中图分类号:TN973.3 文献标识码:A 文章编号:2096-4706(2024)14-0001-04
Research on Inverse Verification Method of Electromagnetic Reconnaissance Simulation Model Based on Data
ZOU Benzhen, CHEN Zhenhua
(Southwest China Research Institute of Electronic Equipment, Chengdu 610036, China)
Abstract: This paper studies the model verification method of how to improve the fidelity of the electromagnetic reconnaissance simulation model. Aiming at the large difference between the traditional electromagnetic reconnaissance model and the actual efficiency, the method of inverse verification for model based on data is proposed by referring to the idea of Digital Twin and construction of black and white box model. It presents a validation algorithm from three aspects of reconnaissance distance, direction finding and data rate of interception, and validates the validation algorithm based on simulation data. The simulation example shows that the proposed method in this paper can solve the fidelity problem of the three effectiveness calculation results in the electromagnetic reconnaissance model, and can play a guiding role in constructing the electromagnetic reconnaissance model with high confidence. At the same time, this method can provide the method reference for other electromagnetic field model verification.
Keywords: model verification; electromagnetic reconnaissance; model data
DOI:10.19850/j.cnki.2096-4706.2024.14.001
0 引 言
传统建模与仿真是基于相似理论,对问题进行抽象后,通过时间轴前推,实现“发现问题或预测未来”的目的。对于电子装备,其很多信号处理、工作过程复杂,对其进行抽象建模很难完全还原其工作过程,因此在建模过程中往往存在很多简化假设;另外装备实际的效能除了受人为操作水平的影响之外,还与作战环境与对抗目标关系很大,有些装备效能往往不能简单地通过算法方程描述。上述这些原因都导致了仿真模型逼真度不够,仿真结果可信度不高。
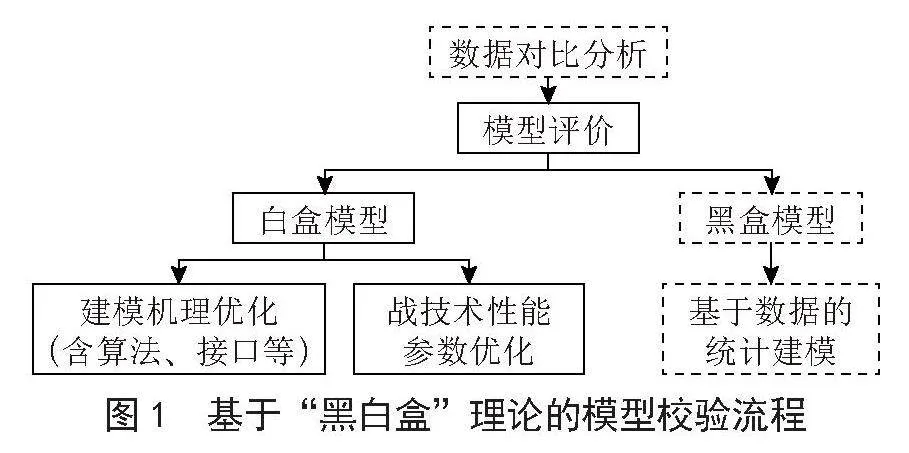
针对这个问题,本文基于数字孪生的思想[1-2],利用装备在产生的实测数据,对比仿真模型的仿真输出数据进行可信度评估,根据评估结果优化模型[3],采用“黑白盒”理论,迭代优化模型的效能指标,持续提升模型逼真度,使得模型能准确地符合实际场景中装备的效能。
1 方法概述
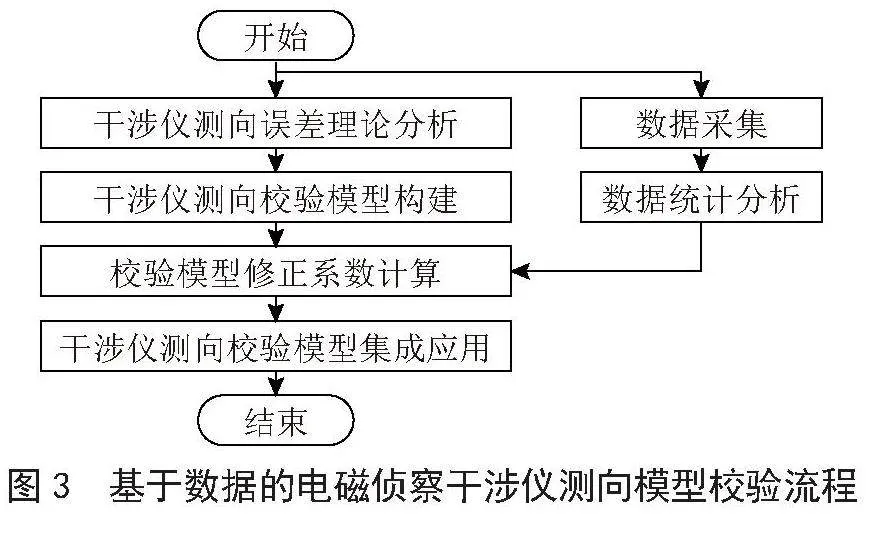
在没有真实数据支撑的情况下,模型的优化只能是不断更加深入地去分析装备的工作流程和原理,以使得抽象的过程更加准确。而在有数据支撑的情况,模型的优化过程可以结合基于传统机理方法的优化和基于统计建模方法的优化这两种方式进行[4]。如图1所示,基于采集的数据可以对模型计算的结果和实际的数据进行对比分析,以此评价和分析建模的逼真度,在此基础上,当评价分析的结果显示是由于模型建模的机理方法、考虑维度、参数配置等原因造成逼真度问题时,可以采用白盒模型的分支,通过正向建模的传统思路对建模的机理方法、模型接口、性能参数等进行调整优化;如果白盒模型无法解决该问题,则应当采取黑盒模型的建模方法,即通过数据的形式代替传统解析算法的形式,以数据为基础,构建统计模型,模型可以加载这些统计数据,当匹配使用的场景时,则可以输出对应的数据。但这有一个问题是数据是持续迭代完善的,即黑盒模型是一个不断完善的建模过程,而传统的白盒模型则不存在此问题。
在模型迭代优化流程中,对于采用传统机理建模方法的模块,若仿真数据与实测数据相差较大,则根据仿真数据和实测数据的差异值,反推模型传统机理建模过程中不合理的地方,并对其进行改进,得到优化后的白盒模块;而对于无法通过传统机理建模得到合理模型的模块,则选取合适的样本,利用第四科学范式的思想,采用统计建模的方法[5],对其进行优化。通过对大量的观测数据建立统计相互关系的规律或数学表达式,建立描述这些统计量之间关系的统计数学模型,得到黑盒模块。最后将白盒模块和黑盒模块组合形成优化后的灰盒模型:
1)传统机理建模优化(白盒模型):通过数据对比和反推,对传统机理建模算法、参数进行优化和校正,形成优化后的白盒模块。
2)基于数据的统计建模优化(黑盒模型):对实装采集数据建立统计数学模型,形成黑盒模块,用于代替原有模型算法和参数。
2 校验算法
电磁侦察能力最重要的是得到对目标的侦察距离、测向误差、定位能力,定位能力一般取决于装备本身的测向误差和定位算法设计。这里主要聚焦侦察作用距离、测向精度和截获数据率三个指标来分析。
2.1 电磁侦察距离计算模型
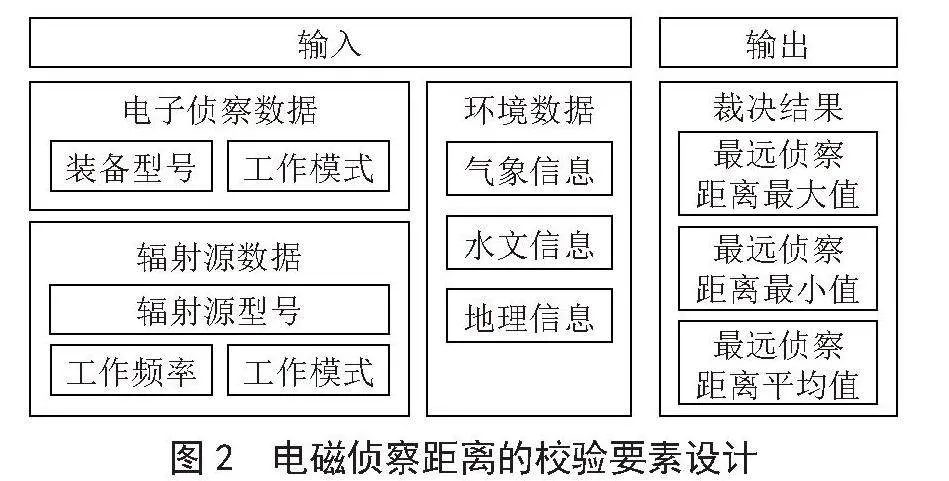
视距条件下,电磁侦察作用距离一般由侦察方程计算[6-7],根据侦察方程,影响侦察装备侦察距离的因素主要是辐射源的辐射参数、空间衰减和装备本身的侦察能力参数这三部分,具体包括发射功率、天线增益、接收增益、波长、检测门限和损耗值组成。而在实际建模过程中,由于对空间衰减建模的简化、装备和目标性能参数不准确等原因,造成理论计算的侦察距离结果与实际情况往往有很大偏差,因此在很多应用场景下使用该侦察方程来计算出的距离值跟很多人的认知存在较大差距。由于对侦察距离的解算需要更多维度的信息,同时对真实物理空间环境的客观抽象建模又存在诸多科学上的门槛,因此可以采用基于黑盒模型的构建方法,通过数据来逆向建模。具体方法是通过对实际数据进行收取和提炼,记录不同环境、不同参数条件下的侦察距离结果,将其数据统计为数据表,以查表的形式代替原有解析函数的形式,而数据表可以长期维护,不断丰富完善,使得模型输出的结果无限逼近真实的客观效能,真正达到在数字空间对物理空间的映射。通过上述方法,即基于对历史数据进行统计分析,可以预测未来“某型电磁侦察装备”在“某种气象地理环境”下对“某型辐射源”的侦察能力。为了对电磁侦察距离进行校验,需要设计试验收集的数据表,如图2所示。电磁侦察距离校验的输入要素包括3个部分,一是侦察数据,主要包括型号和工作模式;二是辐射源数据,主要包括型号、工作频率、工作模式;三是环境数据,包括气象、水文、地理信息。电磁侦察距离校验的输出要素是裁决结果,包括侦察距离的最大值、最小值和平均值。
2.2 测向计算模型
针对电磁侦察中干涉仪测向能力计算,通过理论分析建模和数据校验相结合的方式,构建电磁侦察干涉仪测向模型。
如图3所示,根据天线干涉仪测向原理[8],从理论分析推导出干涉仪测向误差计算模型,在此基础上构造可利用数据进行校验的校验模型。同时,通过采集干涉仪测向数据,对采集的数据进行处理,统计样本方差作为测向误差的估计值[9]。利用不同条件下的侧向误差估计值,基于最小二乘拟合计算得到校验模型中的修正系数,最后应用到干涉仪测向模型的仿真计算中。
根据天线干涉仪测向原理,从理论分析得到干涉仪测向误差σθ:
其中:σφ为相位不一致性误差。
基于干涉仪测向数据,对不同信号频率,不同入射角的测向结果进行统计,利用不同信号频率不同入射角下的干涉仪测向样本方差作为干涉仪测向误差的估计值[10]:
由于实际干涉仪天线的测向误差由系统安装误差、测量误差、圆锥效应、天线和接收通道的相位不一致性误差等各种因素组成,采用理论计算得到的干涉仪测向性能不能准确描述实际情况。以干涉仪测向数据的统计结果,对干涉仪测向误差的计算理论公式进行修正,建立如下校验模型:
这里C1、C2、C3为修正系数,通过对不同频率、不同方位的数据统计结果,采用最小二乘法对模型进行参数拟合,得到最佳的修正系数。利用修正系数外推到不同频段的干涉仪天线测向计算中,实现干涉仪测向的仿真计算。
2.3 截获数据率计算模型
在满足信号截获条件下,电磁侦察输出和上报侦察结果的数据率不只跟天线扫描有关系。辐射源信号经过空间传输达到检测门限后,会再进行信号分选、识别、数据处理等过程,最终将侦察结果上报给上级情报系统,整个处理链路比较复杂。而且在各个传输或处理环节都可能存在误差和不确定性,在仿真建模过程中往往会对这些过程进行简化,因此电磁侦察实际上报的侦察结果的数据率跟理论分析的结论往往无法对应。
在装备执行任务期间,想要得到对特定目标的真实数据上报率,应该假设以上几个情况都不存在,即数据上报率仅与敌我双方天线扫描和一些误差(系统误差、随机误差)有关。而当出现一些间断时长较长的情况时,应该认为已经超出了正常的范围,应当予以排除。
对时间间隔数据按从小到大进行排序,得到时间间隔序列,记为t,假设经过筛选后共有n个数据元素。分析其概率分布函数pdf,记为p = P(t),其中,t = (t1,t2,…,tm),p = (p1,p2,…,pm),ti<ti+1。
根据概率分布函数pdf得到累积分布函数cdf,记为f = F(t),需要说明的是,由于存在各种误差和不确定性,采集的数据可能并不会服从一个特定的数学分布,即无法通过一个数学方程来表达。并且实际的间隔时间是由离散的少量数据组成,这样就会得到间隔时间t与其累积分布函数值f的对应关系表R = {t,f },其中f = ( f1,f2,…,fn)。
生成一个服从均匀分布的随机数U,即,将随机数U带入概率分布函数和累积分布函数,将会得到:P (F -1(U)≤t) = P (U≤F -1(t)) = F(t)。
理论上,对于生成的随机数U,只要将其带入累积分布函数的逆函数,就可以得到与实际数据分布规律一致的时间间隔T,其对应的数学关系为:T = F -1(U) = INF(t:F(t) = U)。
前面分析到,由于累积分布函数是离散和不规律的,因此无法通过数学表达式进行逆解析。另外实际的时间间隔数据本身规模就比较小,因此可以采用查表的方法,直接在累积分布关系表R = {t,f }中查询,当f = U时,其对应的时间间隔t即为想要得到的模拟数据。
3 仿真应用
3.1 电磁侦察距离
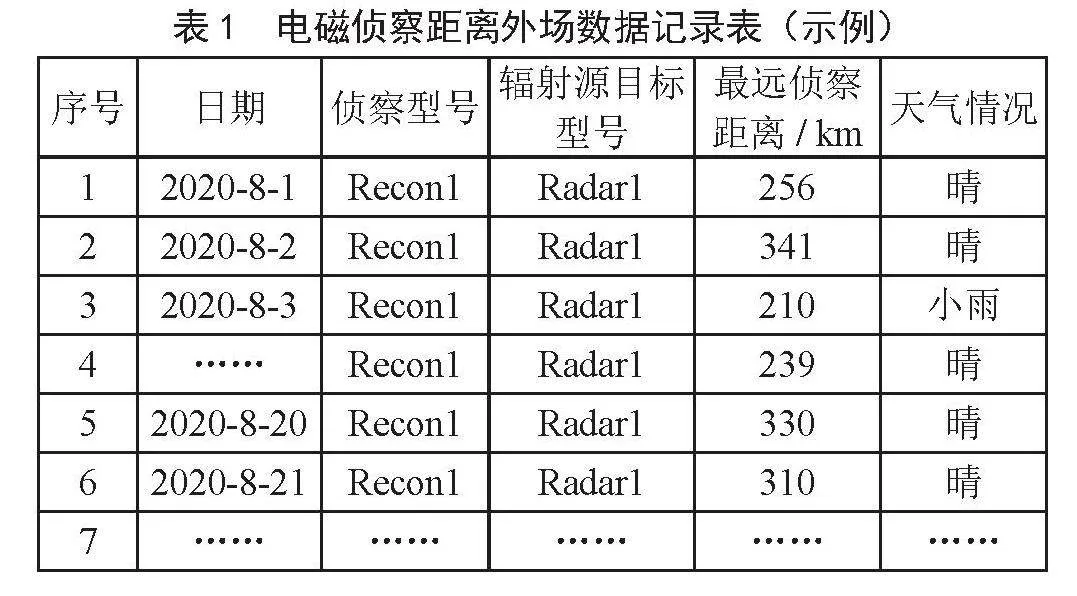
针对外场数据,获取每次执行任务期间对目标截获的最远距离,对该最远距离进行记录和统计如表1所示。
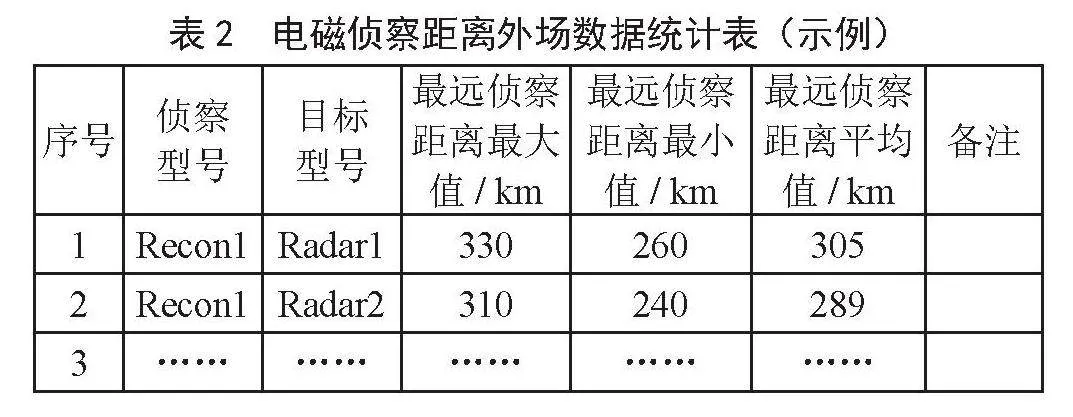
针对外场数据,获取每次执行任务期间对目标截获的最远距离,对该最远距离进行记录和统计如表2所示。输出指标:最远侦察距离最大值、最小值、平均值。
3.2 测向计算模型
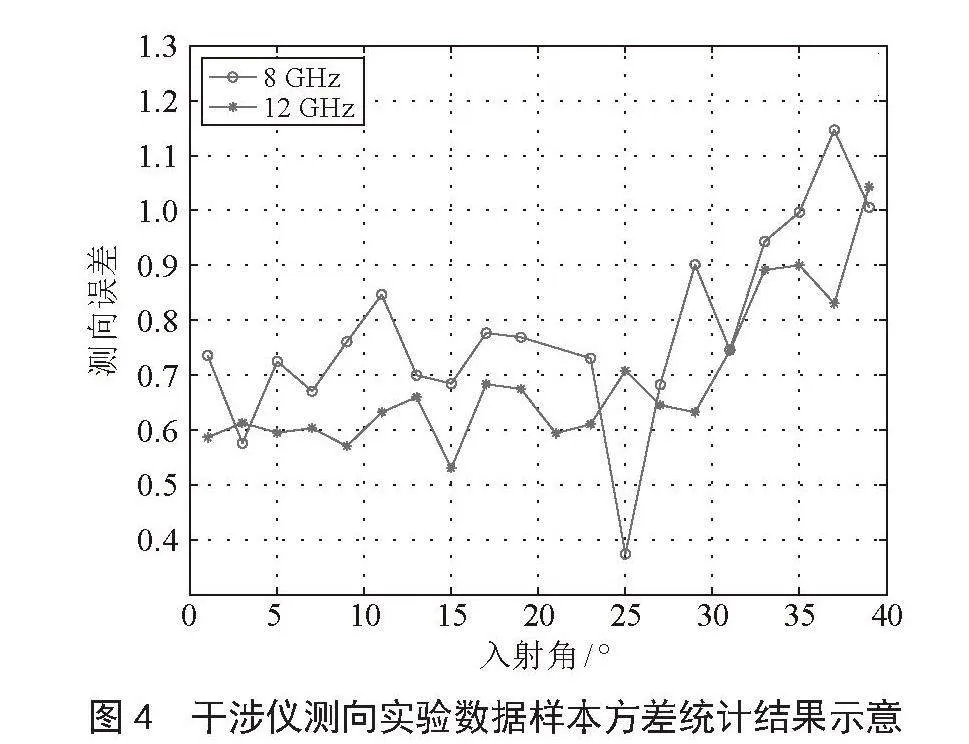
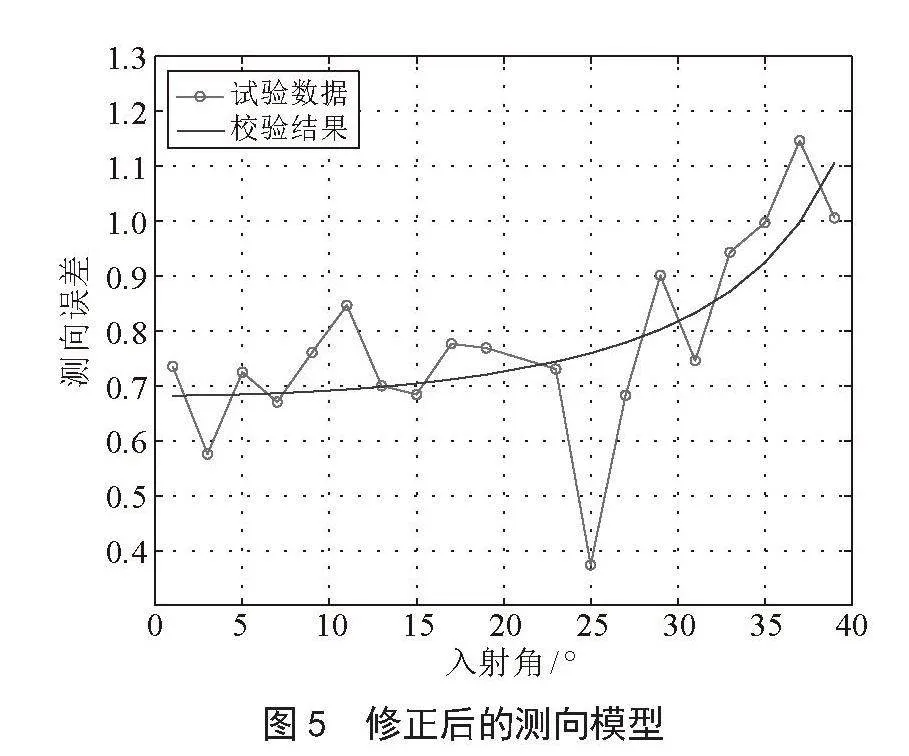
通过干涉仪测向的理论分析,干涉仪测向误差仅与入射角相对干涉仪天线法向的夹角(0°~45°)相关,对原始数据进行处理,将入射角度与45°、135°、225°、315°进行差值,换算到0到45度的范围进行统计处理,得到不同频率(8~16 GHz)、不同入射角(0°~45°)下的测向结果。剔除测向角度中的异常值,利用样本方差计算公式,对不同条件下的测向结果统计样本方差,如图4所示。
基于最小二乘拟合,用统计的数据对构建的校验模型系数进行估计,得到最佳的修正系数,从而得到数据校验后的测向模型,如图5所示。
3.3 截获数据率
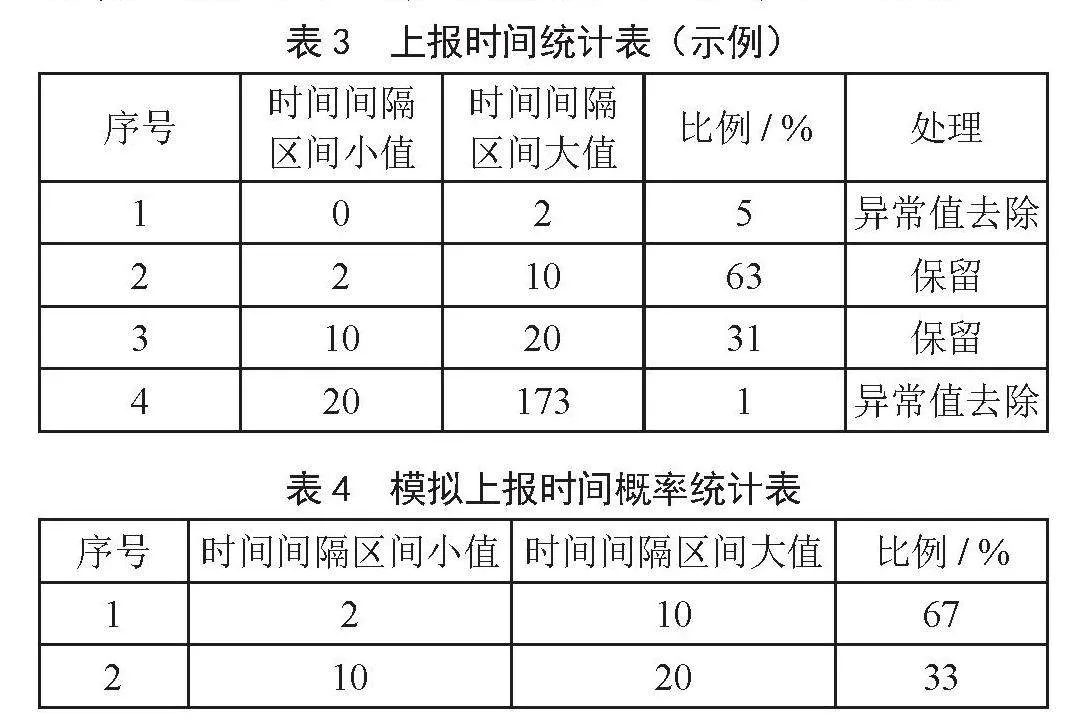
首先采集外场数据,对某型侦察装备对某型目标的上报时间间隔进行统计,仿真示例如表3所示,对数据进行统计及异常值处理。
对表中保留的间隔时间数据按照从小到大的顺序进行排序,并进行概率统计,然后利用ITM逆变换方法生成随机的间隔时间数据,重复执行1 000次。对得到的间隔时间数据进行概率分布统计,并与经过处理后得采集数据进行对比,如表4所示,可以看出模拟的数据与试验采集数据的概率分布是一致的。
4 结 论
针对模型可信度的问题,基于数字孪生的思想,以电磁侦察模型为例,利用采集数据对电磁侦察模型中的侦察、测向和数据上报等能力进行校验优化。本文未来的研究方向将结合人为操作和环境对效能等方面的影响,持续对模型的校验方法进行深入研究。
参考文献:
[1] 杨林瑶,陈思远,王晓,等.数字孪生与平行系统:发展现状、对比及展望 [J].自动化学报,2019,45(11):2001-2031.
[2] 李欣,刘秀,万欣欣.数字孪生应用及安全发展综述 [J].系统仿真学报,2019,31(3):385-392.
[3] 李培林,邹本振,王洪鹏,等.基于机器学习的电子对抗装备跨层次建模技术 [J].电子信息对抗技术,2021,36(6):84-88.
[4] 吴云章,肖阳,王丽萍,等.基于实时数据驱动的低空数字平行战场研究 [J].国防科技,2022,43(6):114-122+134.
[5] 沈远海,黄炳涛,刘曲明.试验数据统计建模研究 [J].舰船电子工程,2004(2):12-14.
[6] 周文辉,闵柏成.舰载雷达对抗设备测向精度试验系统误差分析及修正方法 [J].舰船电子对抗,2019,42(3):30-33+47.
[7] HANNEN P J.雷达与电子战导论:第4版 [M].李轲,卢建斌,包中华,等译.北京:国防工业出版社,2017:25-30.
[8] 范忠亮,胡元奎.阵列单脉冲比幅和干涉仪测向精度比较 [J].雷达科学与技术,2013,11(4):434-436+442.
[9] 李忠良.比幅测向系统截获雷达信号的方位误差 [J].电子对抗,2000(3):7-15.
[10] ADAMY D L.电子战原理与应用 [M].王燕,朱松,译.北京:电子工业出版社,2017.
作者简介:邹本振(1986—),男,汉族,山东泰安人,高级工程师,硕士研究生,研究方向:计算机仿真。
收稿日期:2024-01-09