中图分类号:TN911.7 文献标识码:A 文章编号:2096-4706(2025)08-0006-05
Abstract:Aiming at the problemof high 1 alarm rateand low acuracyof circular array direction finding algorithm underambient noise and multipath interference,this paper proposes aone-dimensional direction finding algorithm basedon high-ordercumulative slicing space sparse representation.Firstly,thealgorithmuses the ideaofExpectation Maximization toconstructahigh-order slicematrixcontaining allthe informationofthe incidentdirectionofthe signal andremoving the redundantinformation,soastorealizethespatialsparsefeaturereconstructionoftheequivalentsignaltrengthinthehighoder cumulativeslcesace.Secondlythroughlinearinterpolationandbilateralinterpolation,theeconstructionquantizatioor is reduced,andthecandidateanglesetandthecorespondingovercompletearraymanifoldmatrixareobained.Theiterative optimizationiscariedout,andthentesecondaryreconstrutioniscarriedout.Finallybasedonteresultsofsatialsparse featurereconstruction,thesignalcomponentsareseparated toachievehig-precisiondirection findingofeachcomponent,nd the complexityofthe algorithm is analyzed.Thesimulationresultsshow thatcompared with the typical sparsereconstruction algorithms,when the Signal-to-Noise Ratio is - 1 0 d B ,the direction finding accuracy of the proposed algorithm is increased by about 4 times,and the angle resolution probability is increased by about 80 %
Keywords:array direction finding; spatial reconstruction; multipath interference; cumulative slicing
0 引言
阵列测向是阵列信号处理的重要分支,具有波束控制灵活、信号增益高及抗干扰能力强的优点,广泛应用于卫星导航、雷达预警和无线电监测等多个领域。阵列测向是一种利用多天线在时域、频域、空域对信号的幅相信息进行联合分析处理的新测向体制,它在多信号、弱信号测向场景中展现了突出优势。然而,随着电磁辐射源空间密度的逐渐增大,阵列测向系统所处的信号环境日益复杂。各天线接收到的环境噪声具有强相关性,且存在与目标信号相干的多径干扰,这会导致信号与噪声子空间能量泄露,使得主流子空间分解类算法的测向性能急剧恶化甚至失效。为摆脱对子空间的依赖,学者们提出了稀疏重构类算法,利用信号的空域稀疏性实现相干信号测向,具备抗多径干扰能力,为阵列测向带来了新的思路。但是,现有稀疏重构类算法对环境噪声敏感,在低信噪比情况下存在性能退化严重、计算复杂度高的问题,无法满足高精度、实时性的需求。因此,本文选取典型的圆阵为研究对象,开展了环境噪声及多径干扰下的阵列测向技术研究。
本文主要针对均匀圆阵在环境噪声及多径干扰下测向虚警高、精度低的问题进行分析。均匀圆阵的阵元均匀分布在平面内的圆环上,能同时满足一维和二维测向需求,并且具备 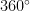 全方位测向的特点,在方位角测向能力上具备各向同性。此外,其阵列结构稀疏,满足设备轻量化需求,具有广阔的应用前景和发展潜力。因此,基于均匀圆阵的阵列测向算法逐渐成为学者们广泛关注的研究热点。不同于均匀线阵,均匀圆阵的阵列流形向量不具备范德蒙特性,因此适用于均匀线阵中对环境噪声和多径干扰的处理方式不再适用于均匀圆阵。模式空间变换的方式可以将均匀圆阵等效为虚拟线阵,使其近似具备均匀线阵的特性,即阵列流形矩阵具备范德蒙特性。文献[1]利用模式空间变换对均匀圆阵接收信号的协方差矩阵进行预处理,再通过波束空间矩阵重构的方式恢复其Toeplitz特性[2],达到解相干的目的,能够处理多径传播带来的相干干扰问题。然而,模式空间变换对阵元数的要求高,仅在阵元数较多的情况下适用。当阵列规模受限时,近似误差大,导致算法测向性能恶化甚至失效。此外,该算法建立在独立高斯白噪声的假设下,对噪声敏感,当环境噪声较强时,测向精度会严重降低。稀疏重构类算法不依赖于子空间分解,充分利用阵列的空间处理能力和信号的空域稀疏特征,可以显著增大信号子空间和噪声子空间的分离度,进而提升阵列的超分辨能力,适用于小样本、低信噪比、相干信号的场景[3-4]。但是同样对环境噪声较敏感,现有算法无法适用于强环境噪声、弱信号的场景[5]。
全方位测向的特点,在方位角测向能力上具备各向同性。此外,其阵列结构稀疏,满足设备轻量化需求,具有广阔的应用前景和发展潜力。因此,基于均匀圆阵的阵列测向算法逐渐成为学者们广泛关注的研究热点。不同于均匀线阵,均匀圆阵的阵列流形向量不具备范德蒙特性,因此适用于均匀线阵中对环境噪声和多径干扰的处理方式不再适用于均匀圆阵。模式空间变换的方式可以将均匀圆阵等效为虚拟线阵,使其近似具备均匀线阵的特性,即阵列流形矩阵具备范德蒙特性。文献[1]利用模式空间变换对均匀圆阵接收信号的协方差矩阵进行预处理,再通过波束空间矩阵重构的方式恢复其Toeplitz特性[2],达到解相干的目的,能够处理多径传播带来的相干干扰问题。然而,模式空间变换对阵元数的要求高,仅在阵元数较多的情况下适用。当阵列规模受限时,近似误差大,导致算法测向性能恶化甚至失效。此外,该算法建立在独立高斯白噪声的假设下,对噪声敏感,当环境噪声较强时,测向精度会严重降低。稀疏重构类算法不依赖于子空间分解,充分利用阵列的空间处理能力和信号的空域稀疏特征,可以显著增大信号子空间和噪声子空间的分离度,进而提升阵列的超分辨能力,适用于小样本、低信噪比、相干信号的场景[3-4]。但是同样对环境噪声较敏感,现有算法无法适用于强环境噪声、弱信号的场景[5]。
针对以上分析,本文提出了面向圆阵的高阶累积切片空间稀疏表示测向算法,利用环境噪声的高斯特性,通过高阶累积切片矩阵对环境噪声进行抑制,并基于此建立高阶累积切片空间稀疏贝叶斯模型,重构其空域稀疏特征,以准确的空域稀疏特征重构结果为基础进行高精度测向。
高阶累积切片矩阵构造
均匀圆阵由多个均匀分布在圆环上的天线阵元构成,假设圆环的半径为 R ,以其圆心为坐标原点建立直角坐标系。假设 M 阵元均匀圆阵位于XOY平面,以 X 轴上的阵元为首,沿逆时针方向分别标号为{1,2,3,…, $M _ { ☉ }$ ,将各阵元与圆心相连,其连线和 X 轴的夹角 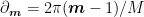 ,其中, m = 1 ,2,…,
,其中, m = 1 ,2,…, 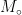
假设有 D 个远场窄带信号从不同的方向同时入射至阵列,方位角定义为入射信号在XOY平面内的投影与X轴的夹角,俯仰角定义为入射信号与XOY平面的夹角,因此信号的入射方向可以表示为 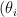
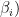 ,其中,
,其中, 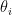 为方位角,
为方位角, 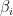 为俯仰角, i = 1 ,2,…,D 。通常情况下
为俯仰角, i = 1 ,2,…,D 。通常情况下 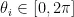 ,
, 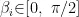 。一维测向时,俯仰角为0,仅考虑方位角的估计。以圆心为相位参考点,均匀圆阵的阵列流形矩阵可以表示为:
。一维测向时,俯仰角为0,仅考虑方位角的估计。以圆心为相位参考点,均匀圆阵的阵列流形矩阵可以表示为:
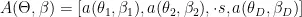
其中, 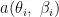 为阵列流向量,其表达式为:
为阵列流向量,其表达式为:
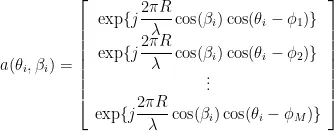
考虑均匀圆阵应用于一维测向时的算法创新,适用的场景为远距离测向,俯仰角可以忽略不计,因此在本文讨论的测向算法中,均匀圆阵的阵列输出信号模型为:
X ( t ) = A ( Θ ) S ( t ) + N ( t )
其中, S ( t ) 为入射信号, N ( t ) 为环境噪声信号。根据高阶累积量的定义和性质,可以推出阵列输出信号 X ( t ) 的四阶累积量为:
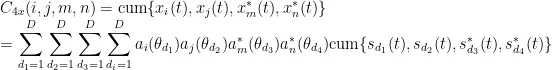
传统的稀疏重构思想构造时需要假设入射信号相互独立,当多径干扰存在时,算法即会失效。利用式(4)的结果,对于 M 阵元的阵列, i , j , m , n 均为正整数。
由环境噪声的高斯特性可知,高阶累积量可以用来抑制噪声。根据高阶累积量的性质,构造出包含信号入射方向全部信息并去除冗余信息的高阶切片矩阵为:
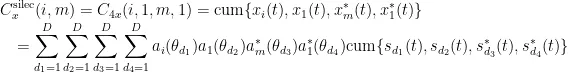
2 算法实现
高阶累积切片矩阵的空域稀疏重构过程建立在离散角度完备集  上,可得到等效信号强度的空域离散分布情况。而DOA估计问题本质上是连续角度估计,离散角度网格会引入无法避免的量化误差。同时,稀疏特征重构过程注重对观测数据拟合的整体误差,而测向问题更关注单个分量的精准估计,因此需要基于空域稀疏特征,进行高精度测向。
上,可得到等效信号强度的空域离散分布情况。而DOA估计问题本质上是连续角度估计,离散角度网格会引入无法避免的量化误差。同时,稀疏特征重构过程注重对观测数据拟合的整体误差,而测向问题更关注单个分量的精准估计,因此需要基于空域稀疏特征,进行高精度测向。
为了满足RIP约束条件,避免由于角度间隔太小使得超完备阵列流形矩阵的列相关性增强。从而导致重构性能恶化,一般情况下角度间隔取值存在下限。这会导致量化误差无法被忽视,直接影响到测向精度。本文利用线性插值与双边插值相结合的方式,降低离格情况下量化误差带来的影响。根据空域稀疏特征的重构结果y,选取前M-1个最大的谱峰。在信源数D未知时,阵元数为 M 的阵列最多能处理的信号个数为 M - 1 。
本文所述面向圆阵的高阶累积切片空间稀疏表示测向算法的流程图如图1所示。算法首先利用EM思想实现高阶累积切片空间中等效信号强度的空域稀疏特征重构,再通过线性插值及双边插值降低重构量化误差并进行二次重构,最后基于空域稀疏特征重构结果,将信号分量进行分离,实现各个分量的高精度测向。
开始 获得备选角度集Ωnen+初始化γ,²),Ω迭代次数 i = 1 EM思想迭代更新?EM思想迭代更新 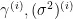 是否满足√ 收敛条件i=i+1上获得空域稀疏重构结果是否满足收敛条件 ↓分离信号分量高精度侧向√√线性插值双边插值 输出测向结果
是否满足√ 收敛条件i=i+1上获得空域稀疏重构结果是否满足收敛条件 ↓分离信号分量高精度侧向√√线性插值双边插值 输出测向结果
目标函数为:
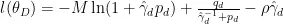
其中 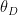 为入射角,
为入射角, 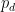 和
和 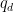 为关于
为关于 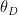 的中间变量。算法1:面向圆阵的高阶累积切片空间稀疏表示测向算法输入:阵列接收数据的高阶累积切片矩阵
的中间变量。算法1:面向圆阵的高阶累积切片空间稀疏表示测向算法输入:阵列接收数据的高阶累积切片矩阵 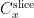 。输出:测向结果
。输出:测向结果 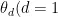 ,2,3,…, D ) 。Part1空域稀疏特征重构如:
,2,3,…, D ) 。Part1空域稀疏特征重构如:
1)构建角度完备集 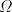 及其对应的超完备阵列流形矩阵A
及其对应的超完备阵列流形矩阵A
2)初始化 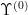 和迭代次数
和迭代次数 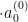 ,确定固定参数
,确定固定参数 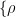 ,a,
,a, 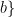 、收敛门限
、收敛门限 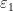 及最大迭代次
及最大迭代次 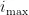 0
0
3)while 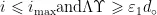
4) 更新 Υ 。
5) 更新 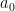 。6)更新 i = i+1 ,
。6)更新 i = i+1 , 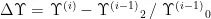 (207) end while。8)return重构结果。Part2多重插值及二次重构如:1)进行线性插值及双边插值。2)获得备选角度集
(207) end while。8)return重构结果。Part2多重插值及二次重构如:1)进行线性插值及双边插值。2)获得备选角度集 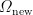 及其对应的超完备阵列
及其对应的超完备阵列
流形矩阵A。3)初始化Y及迭代次数 j ,确定收敛门限 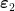 及
及
最大迭代次数 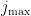 。4) while
。4) while 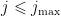 and
and 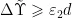 。5) 更新Y。6 更新 j=j+1 ,
。5) 更新Y。6 更新 j=j+1 , 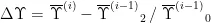 7) end while。8)return 重构结果。Part3信号分离及高精度测向如:1)得到高精度测向范围。2)对目标信号分量进行分离。3)基于空域稀疏特征的二次重构结果,实现各
7) end while。8)return 重构结果。Part3信号分离及高精度测向如:1)得到高精度测向范围。2)对目标信号分量进行分离。3)基于空域稀疏特征的二次重构结果,实现各
分量的高精度测向。4)return测向结果。
3 计算复杂度分析
算法的计算复杂度是指运行算法所需的资源量,主要包括CPU运行时间和内存占用空间。在阵列测向算法中,计算复杂度常被作为衡量性能的重要指标。其中,时间复杂度,即CPU运行时间,常被重点关注。本小节根据上小节中分析的算法流程及具体步骤,分析所提算法的时间复杂度,其衡量标准为算法所需的复数乘法次数。
根据算法的结构可知,总计算复杂度是三个部分计算复杂度的总和。影响算法中矩阵维度的量有阵元个数 M . 、信源个数 D 、角度完备集大小 F 和备选角度集大小 $\boldsymbol { \cdot } \overbar { F }$ ,通常 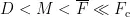 。Partl的计算复杂度由单次迭代的计算量和迭代收敛速度共同决定。综合每个步骤的计算复杂度,并忽略常数项及低次项,Partl中单次迭代的计算复杂度为
。Partl的计算复杂度由单次迭代的计算量和迭代收敛速度共同决定。综合每个步骤的计算复杂度,并忽略常数项及低次项,Partl中单次迭代的计算复杂度为 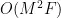 。算法的收敛速度极大程度影响了计算复杂度,其计算复杂度与达到收敛条件所需的迭代次数成正比,但是关于算法收敛性的分析大多是定性的,很难定量,因为算法实际运行过程中,所处理的信号与环境噪声特点、参数初始化及收敛门限的大小均会对迭代次数造成影响。不动点迭代方式能极大程度加快收敛速度,提高重构结果的稀疏性,其具体分析也将在后续仿真实验中给出。这里先假设Part1重构过程达到收敛时的迭代次数为
。算法的收敛速度极大程度影响了计算复杂度,其计算复杂度与达到收敛条件所需的迭代次数成正比,但是关于算法收敛性的分析大多是定性的,很难定量,因为算法实际运行过程中,所处理的信号与环境噪声特点、参数初始化及收敛门限的大小均会对迭代次数造成影响。不动点迭代方式能极大程度加快收敛速度,提高重构结果的稀疏性,其具体分析也将在后续仿真实验中给出。这里先假设Part1重构过程达到收敛时的迭代次数为 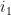 ,则可得到其计算复杂度为
,则可得到其计算复杂度为 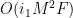 。Part2中多重插值的计算复杂度可以忽略,二次重构过程的复数乘法次数分析与Part1类似,假设其迭代次数为
。Part2中多重插值的计算复杂度可以忽略,二次重构过程的复数乘法次数分析与Part1类似,假设其迭代次数为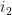 ,则有其计算复杂度为
,则有其计算复杂度为 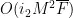 。Part3中,假设在单分离的高精度测向范围内搜索的点数为
。Part3中,假设在单分离的高精度测向范围内搜索的点数为 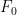 ,则算法需要在
,则算法需要在 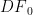 个角度值上对目标函数进行计算,因此其计算复杂度为
个角度值上对目标函数进行计算,因此其计算复杂度为 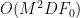 。
。
综上,本文所提算法的计算复杂度为上述三部分之和: 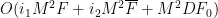 。
。
4仿真分析
本节将借助仿真实验对本文所提测向算法的性能进行评估,选取的性能指标主要为测向均方根误差(RMSE)和正确分辨概率(PR)。为了证明所提算法的优越性,本文选取了现有的典型算法作为参考对象,主要包括 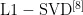 、OGSB[]、PSBL[10]Correlate-VBI[11]以及SAMV2和 SAMV2-SML算法[12]。计算相应条件下的克拉美罗下界(CRLB)作为理论性能下限。本节中的仿真实验使用的阵列是一个7阵元的均匀圆阵,其半径为 1 7 0 m m ,接收的信号是常见的 2 . 4 G H z 无线频段信号,采用BPSK调制方式。由于本节中所对比的算法均是稀疏重构类,不失一般性地,将整个空域
、OGSB[]、PSBL[10]Correlate-VBI[11]以及SAMV2和 SAMV2-SML算法[12]。计算相应条件下的克拉美罗下界(CRLB)作为理论性能下限。本节中的仿真实验使用的阵列是一个7阵元的均匀圆阵,其半径为 1 7 0 m m ,接收的信号是常见的 2 . 4 G H z 无线频段信号,采用BPSK调制方式。由于本节中所对比的算法均是稀疏重构类,不失一般性地,将整个空域  ,
, 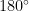 )固定间隔
)固定间隔 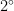 划分为180个可能的角度取值。
划分为180个可能的角度取值。
同时,为了降低算法的计算时间,将本文所提算法第一次重构的最大迭代次数设置为100,收敛门限设置为0.01,二次重构的最大迭代次数设为500,收敛门限设为0.001。其他对比算法的初始化方式均按照相应论文中规定进行,并且统一设置算法的最大迭代次数和收敛门限。算法在MATLAB2020a中运行,计算环境的配置为IntelCorei5-12450H,C P U@ 4 . 4 0 G H z. 9
在环境噪声及多径干扰条件下,通过仿真实验对比不同算法的性能。假设有两个信号同时入射到阵列上,其真实DOA分别为 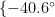 ,
, 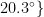 ,幅度分别设置为1和0.8,观测时间内采样点数为512。在以下场景下进行仿真实验:环境噪声相关系数为0.8,一个信号为另一信号的多径干扰,即两个信号相干,幅度衰减因子分别为{1,0.8},相位差为
,幅度分别设置为1和0.8,观测时间内采样点数为512。在以下场景下进行仿真实验:环境噪声相关系数为0.8,一个信号为另一信号的多径干扰,即两个信号相干,幅度衰减因子分别为{1,0.8},相位差为 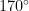 ,信噪比从 - 1 0 d B 逐渐变化至 1 0 d B ,通过500次蒙特卡洛试验,计算各算法的均方根误差(RMSE)和正确分辨概率(PR),结果如图2、图3所示。
,信噪比从 - 1 0 d B 逐渐变化至 1 0 d B ,通过500次蒙特卡洛试验,计算各算法的均方根误差(RMSE)和正确分辨概率(PR),结果如图2、图3所示。
从图2可以看出,L1-SVD算法的性能最差,其没有利用稀疏贝叶斯假设,仅靠正则化参数来控制信号的空域稀疏性,这相比稀疏贝叶斯类算法有明显的劣势。OGSB的性能在低信噪比下恶化较快。其次,在理想条件下,SAMV2-SML的性能优于SAMV2,但在本文所关注的环境噪声及多径干扰条件下,其性能出现了明显的恶化,在信噪比 - 1 0 d B 到 1 0 d B 之间均比SAMV2算法的性能差。在高信噪比范围内,即信噪比高于 - 4 d B 时,所提算法及PSBL、Correlate-VBI算法表现优异,其RMSE均在 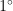 以内;但当信噪比低于-4dB时,PSBL、Correlate-VBI算法的性能将快速恶化,而所提算法仍能保持较高的测向精度。从整个信噪比变化范围来看,所提算法具有最高的测向精度,是最接近CRLB的。并且在信噪比为 -1 0 d B 时,所提算法的RMSE接近
以内;但当信噪比低于-4dB时,PSBL、Correlate-VBI算法的性能将快速恶化,而所提算法仍能保持较高的测向精度。从整个信噪比变化范围来看,所提算法具有最高的测向精度,是最接近CRLB的。并且在信噪比为 -1 0 d B 时,所提算法的RMSE接近 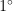 ,低于其他几种算法的1/4,即相比较而言,所提算法的测向精度提升了4倍。
,低于其他几种算法的1/4,即相比较而言,所提算法的测向精度提升了4倍。
图3显示的是不同算法的正确分辨概率随信噪比的变化。从图中可以明显着出,所提算法能适应的信噪比最低,当信噪比为 - 1 0 d B 时,本文算法的分辨概率超过 80 % ,显著高于其他算法。在这种情况下,其他算法的分辨能力基本上已经丧失。其中,L1-SVD和OGSB的分辨性能最差,SAMV2-SML的分辨概率在信噪比低于 6 d B 时开始出现下降,SAMV2紧随其后,在信噪比为 2 d B 时出现下降趋势。PSBL和Correlate-VBI的表现较优异,能够适应的最低信噪比在 - 5 d B 左右,而所提算法则在 - 1 0 d B 时仍能保持较高的分辨概率。
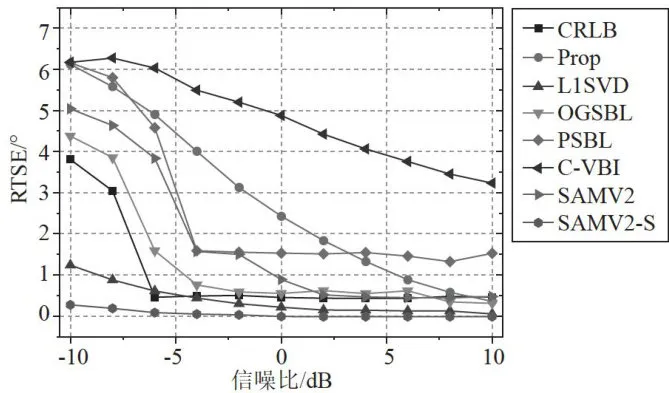 图2不同算法的RMSE随信噪比变化示意图
图2不同算法的RMSE随信噪比变化示意图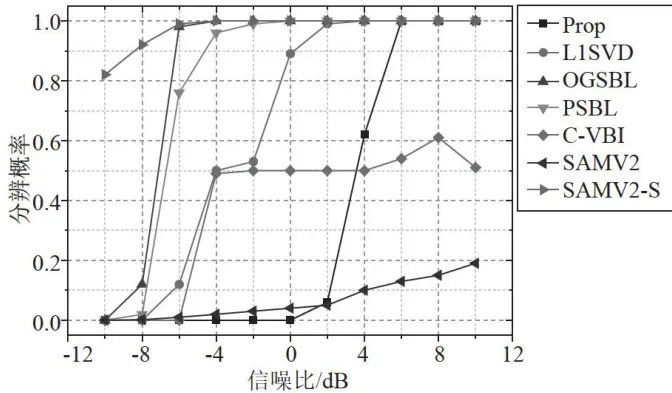 图3不同算法的PR随信噪比变化示意图
图3不同算法的PR随信噪比变化示意图5结论
本文针对圆阵测向算法受环境噪声及多径干扰的影响测向虚警高、精度低的问题,提出了高阶累积切片空间稀疏表示一维测向算法利用环境噪声的高斯特性,通过高阶累积切片矩阵对环境噪声进行抑制,并基于此建立高阶累积切片空间稀疏贝叶斯模型,重构其空域稀疏特征,以准确的空域稀疏特征重构结果为基础进行高精度测向。借助仿真实验对本文所提测向算法的性能进行评估,结果显示,相比典型稀疏重构类算法,信噪比为-10dB时,所提算法的测向精度提升约4倍,角度分辨概率提升约 80 % 。未来工作中,可以考虑将本文结果扩展到二维测向领域,通过构建动态感知矩阵实现高精度测向。
参考文献:
[1]张薇.基于矩阵重构的相干信源波达方向估计算法研究[D].哈尔滨:哈尔滨工业大学,2021.
[2]张龙,刘杨远,唐晓红,等.基于概率切片累积特征的轴承双向传感器信息融合故障诊断[J].计算机集成制造系统,2023,29(8):2722-2732.
[3]夏楠,马昕昕,王思琦.强干扰下基于三阶互累积量的FMCW雷达信号DOA估计算法[J].电子学报,2024,52(2):510-517.
[4]袁伟力,汤新民,顾俊伟.基于天线方向性参数辨识的航空器测向研究[J].系统工程与电子技术,2024,46(7):2446-2455.107070.
[5]崔宏,马杰.不同阵列布局的空间谱测向方法的抗多径性能研究[J].无线电工程,2023,53(12):2765-2770.
[6]范广伟,王永杰,王飞.一种基于多天线测向的欺骗干扰抑制方法[J].计算机仿真,2023,40(9):158-161+175.
[7]张紫晗,赵文杰,黄永辉,等.一种基于低成本软件无线电的二维测向系统设计[J].电讯技术,2023,63(6):831-836.
[8]CHENX,XUHT,ZHANGYF,etal.Sequential Recommendation with User Memory Networks [C]//Proceedings oftheEleventhACMInternational ConferenceonWeb Searchand DataMining.NewYork:,2018:108-116.
[9]YANGZ,XIELH,ZHANGCS.Off-grid DirectionofArrival Estimation Using Sparse Bayesian Inference [J].IEEETransactions on Signal Processing,2013,61 (1):38-43.
[10]WUXH,ZHUWP,YANJ.DirectionofArrivalEstimation forOff-Grid SignalsBased onSparse BayesianLeaming[J].IEEESensorsJournal,2016,16(7):2004-2016.
[11]CAOZ,DAIJS,XUWC,etal.FastVariationalBayesianInferenceforTemporallyCorrelatedSparseSignalRecovery[J].IEEE Signal ProcessingLetters,2021,28:214-218.
[12]ABEIDAH,ZHANGQL,LIJ,etal.Iterative Sparse Asymptotic Minimum Variance BasedApproachesfor Array Processing[J].IEEE Transactions on Signal Processing, 2013,61(4):933-944.
作者简介:周烨(1992一),女,汉族,山东济南人,助理工程师,本科,研究方向:信息安全、抗干扰。