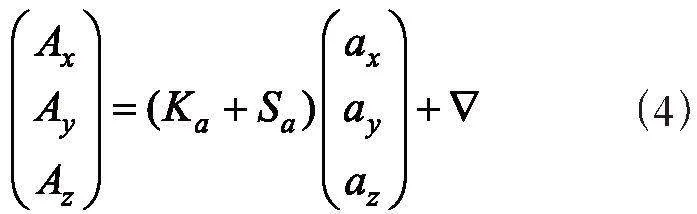
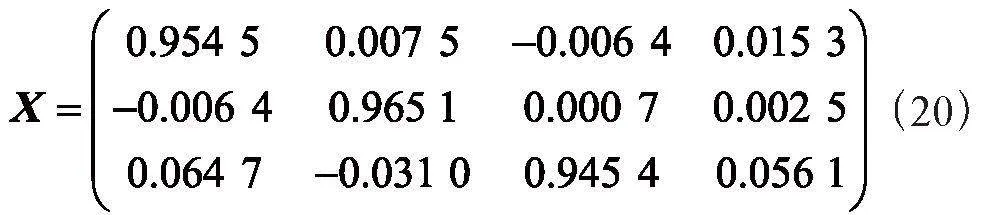
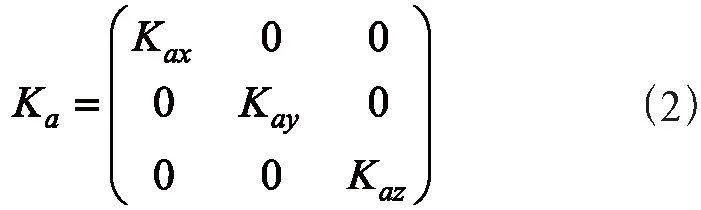
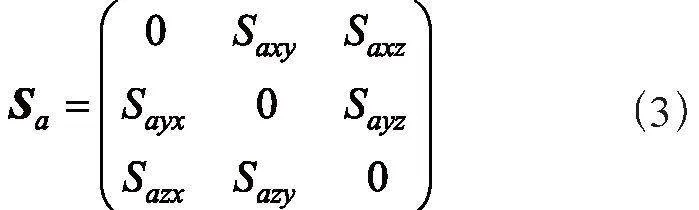
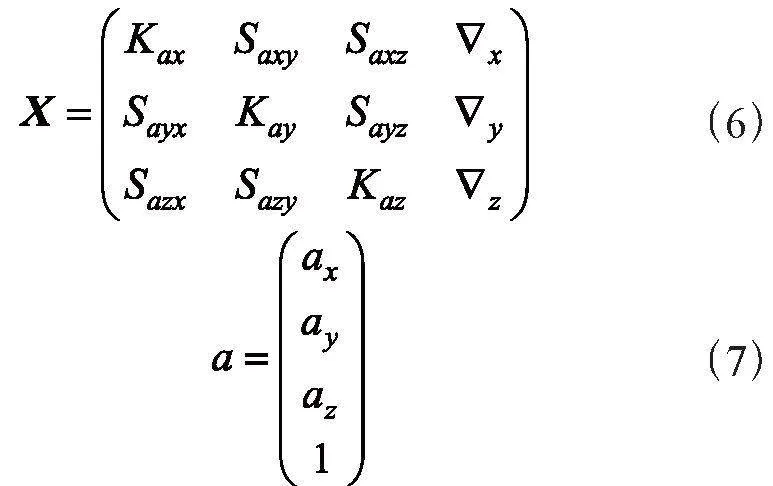
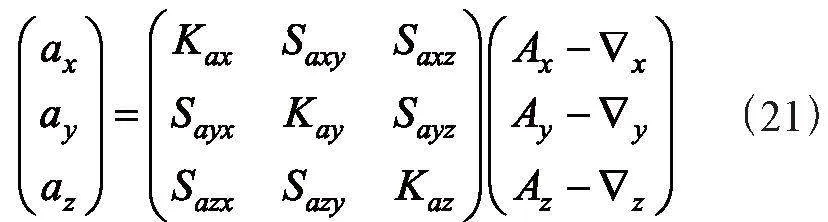
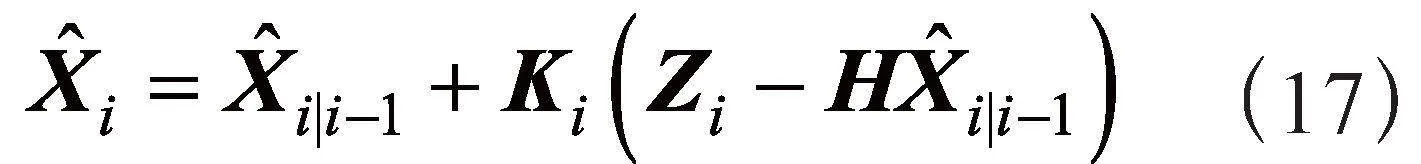
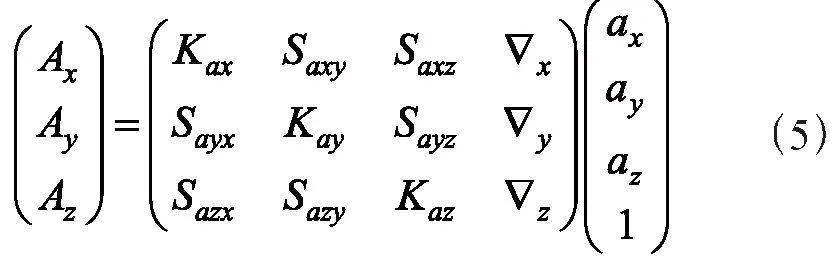
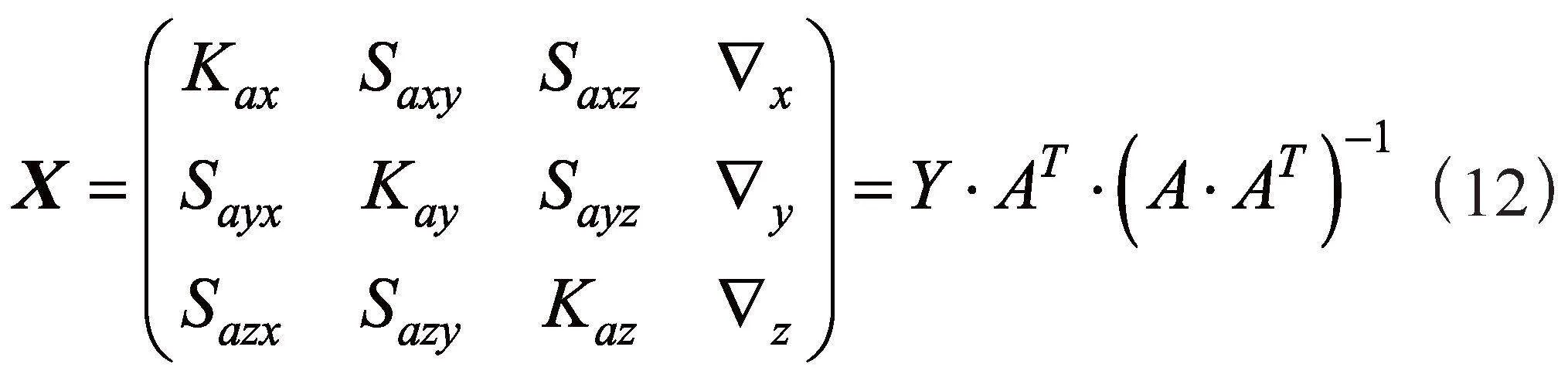


摘 要:MEMS传感器以其体积小、廉价等优点备受关注,然而,其误差相对较高。由于相同规格的MEMS惯性传感器存在误差特性的差异,建立准确的传感器误差模型成为一项颇具挑战性的任务。低准确度的MEMS惯性传感器误差,主要涉及零偏、标准化规范影响因数和相对较大的安装偏差。为克服这种误差源,文章提出一种采用Kalman滤波和六位法的MEMS加速度计补偿方法。实验结果表明,MEMS加速度计在补偿后输出的误差明显减小。横滚角在-90°~+90°范围内变化的绝对误差在应用该方法后,由补偿前的2.44°减小至0.64°。
关键词:六位置法;卡尔曼滤波;MEMS加速度计;标定
中图分类号:TP212;TH824 文献标识码:A 文章编号:2096-4706(2024)16-0010-05
Compensation Method of MEMS Accelerometer Based on Six-position Method and KF
Abstract: MEMS sensors have attracted much attention because of their advantages such as small size and low cost. However, their error level is relatively high. Due to the difference in error characteristics of MEMS inertial sensors with the same specifications, it is a challenging task to establish an accurate sensor error model. The low accuracy MEMS inertial sensor error mainly involves zero bias, standardized specification influence factor and relatively large installation deviation. To overcome this error so7l0fVW/r5rS/MSFFeQ36QKGanNK7bpHzgqWBkZ5z7V4=urce, a MEMS accelerometer compensation method using Kalman filtering and six-position method is proposed. The experimental results show that the output error of MEMS accelerometer is obviously reduced after compensation. The absolute error of roll angle in the range of -90° to +90° is reduced from 2.44° before the compensation to 0.64° by applying the proposed method.
Keywords: six-position method; Kalman filtering; MEMS accelerometer; calibration
0 引 言
MEMS惯性传感器以其紧凑的体积、轻量化设计、经济实惠以及高度可靠性等特性,显著推动了微型化和智能化技术的发展。这些传感器在汽车、导弹以及电子产品等多个领域得到了广泛应用。MEMS传感器的研究对于实现高性能、低成本的微型化设备以及智能化系统至关重要。
尽管MEMS加速度计面临零偏、刻度因子和安装误差等方面的主要误差问题[1-3],但通过建立其相关误差模型并实时进行误差补偿和修正,能够有效地应对这些挑战,以确保传感器输出的准确性和可靠性。在不断发展的科技前沿,对于MEMS惯性传感器的研究和创新不仅对提高传感器性能、拓展应用领域具有重要推动作用,同时也促进了微型化技术和智能系统的不断演进。这为未来科技应用带来了更广阔的发展空间,为实现智能化、高效化的技术解决方案奠定了坚实的基础。
1 原理和方法
1.1 MEMS加速度计的误差与标定
1.1.1 MEMS加速度计误差来源
1)常值零偏。常值零偏漂移误差是指加速度计在输入为零时,输出端的输出信号称为常值零偏漂移误差,加速度计的常值零偏漂移误差不受加速度计任何方向运动的影响[4]。常值零偏的发生往往受多个因素的影响,如加速度计质量块的折叠梁存在的加工偏差和敏感电极之间存在的寄生电容,它们也是引入零偏的一个重要因素。因此,加速度计的零偏可通过式(1)来描述:
其中,∇x、∇y、∇z为加速度计三轴常值零偏。
2)标度因数。标度因数受多种因素的综合影响,其中温度对硅材料的MEMS传感器件的影响尤为显著。这是因为温度的波动会对硅材料的微结构尺寸及杨氏模量等参数带来变化。由于敏感电容与位移之间存在非线性关系,因此可将标度因数分为两大类:非线性误差(Nonlinear Mission)和温度误差(Temperature Mission)。此外,折叠梁加工尺寸不一致、微弱信号探测放大环节等MEMS惯性器件中的因素,也可能导致各测量轴因数量不一致而导致标度不一致[5]。加速度计的标度因数可通过式(2)表示:
其中,Kax、Kay、Kaz为加速度计三测量轴的标度因数。
3)安装误差。微型MEMS惯性传感器通常巧妙地集成在芯片内,这一封装方式使其在各类应用中变得更加灵活和普适。然而,这种微小封装也引入了一项主要挑战,即安装误差。在MEMS惯性器件的运用中,精确描述安装误差对其性能的影响至关重要。
可以通过描述惯性测量单元内的3个敏感轴相对于载体坐标系的相对角速度关系来实现对与安装误差的描述。这3个敏感轴通常沿X、Y和Z方向,它们的测量结果直接受到外部载体运动的干扰。在考虑安装误差时,关注这3个轴在MEMS坐标系和载体坐标系之间的相对角速度,这有助于更准确地理解和纠正由于安装引起的误差。
通过深入研究这些相对关系,可以建立相应的坐标变换模型,从而更好地理解MEMS传感器在不同应用场景中的性能特征。这有助于采取有效的校准和补偿措施,确保传感器在实际使用中具有可靠的测量性能。相应的坐标变换矩阵可使用式(3)表示:
其中,Saxy、Saxz、Sayx、Sayz、Sazx、Sazy为加速度计安装误差参数。
1.1.2 MEMS加速度计误差模型
基于前文对MEMS加速度计误差的分析,可以构建MEMS加速度计输出误差的数学模型,具体表达如式(4)所示:
其中,Ax、Ay、Az为加速度计三轴的输出值,ax、ay、az为加速度计三轴测量的真实值。
1.1.3 MEMS加速度计标定方法
针对MEMS加速度计标定方法,许多学者进行了相关的研究。中国电子科技集团公司第五十四研究所的贾继超等人针对现有标定方法在加速度计非线性误差参数发生变化时无法满足免拆卸高精度标定的问题,设计了一种基于双轴精密离心机和捷联惯导系统转位机构交替旋转、依靠转位机构实现9位置标定路径的系统级标定方法,可实现加速度计二次项、交叉耦合项共9个非线性误差参数系统级高精度标定[6]。海军航空大学的鹿珂珂等人提出了174dfc00d34d2fb3fe1e8ed760a645ab一种不依赖精密转台的MEMS-IMU误差标定补偿方法,使用Allan方差分析方法确定随机误差参数;采用与视觉融合的非线性优化方法在线实时估计并补偿零偏,最终达到提高定位精度的目的[7]。基于前文讨论的加速度计误差模型,将式(4)经过变形可得式(5):
令:
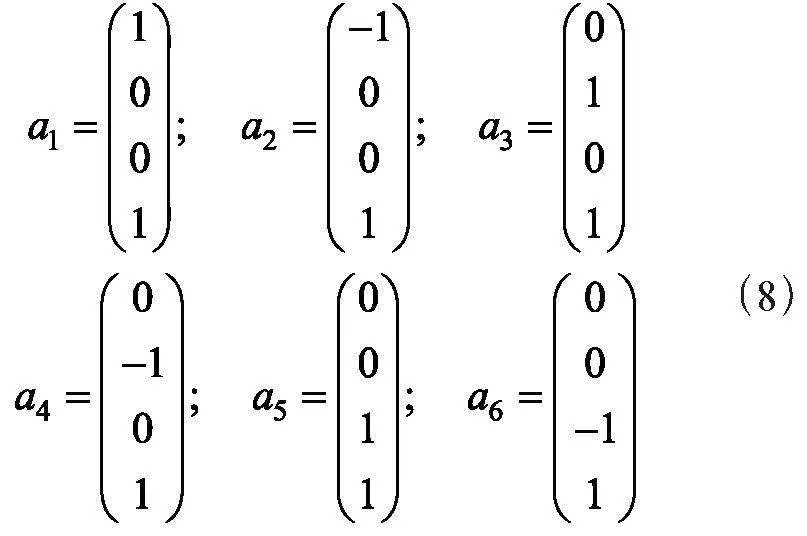
因此,矩阵X即为基于加速度计的标定需求确定的参数。本文所使用的MEMS加速度计量程为±2 g,采用以下标定方法:在双轴转台上进行了6个不同位置的翻转,使得重力方向与加速度计的3个敏感轴方向重合。所设计的6个位置下,加速度计3个敏感轴的测量值分别为g和-g[8]。通过使用转台,使MEMS加速度计在每个位置保持静止大约1分钟,以采集相应的数据。这个过程旨在确保对于各个轴的重力响应的准确测量。获得6次数据采集信息,可以单独记录为:
令:
加速度计在六位置时的实际输出可用式(10)表示:
其中:
分别表示加速度计在第i个静止时刻的输出值。在本文中,进行了维持1分钟的加速度计输出数据测量,并将其平均值作为第i个静止时刻的加速度计输出值。在标定实验中,将MEMS加速度计固定在双轴转台上进行旋转。
矩阵X可以根据最小二乘法求得,如式(12)所示:
1.2 Kalman滤波原理
卡尔曼滤波是一种基于最小化误差协方差准则的最优估计方法,其独特之处在于计算效率高且具有出色的实时性。这一滤波技术通过连续修正未来运动状态的估计值,充分利用实际的运动参数,以提升对系统状态的准确估计。同时,卡尔曼滤波在保持实时性和稳定性方面找到了一种优雅的平衡。其核心思想是通过融合测量值和先验估计,以及考虑系统动态模型,来计算最优估计。这样的动态估计不仅能够有效抵抗噪声的干扰,而且能够在时变环境下保持高度鲁棒性。相比于一些传统的滤波方法,卡尔曼滤波的独到之处在于其对系统的动态变化有更为敏锐的感知。通过动态调整滤波器的增益,卡尔曼滤波能够适应不同运动模式和系统状态的变化,从而在估计过程中更为灵活和准确。卡尔曼滤波器的状态方程和测量方程通常以以下形式表示[9]:
式中,A为状态转移矩阵;H为测量矩阵;W、V分别为状态和测量的噪声矩阵,其方差分别为Q、R。状态向量预测方程为:
状态向量协方差矩阵预测为:
状态向量更新方程为:
状态向量协方差更新方程为:
Kalman增益矩阵为:
2 实验平台与结果分析
2.1 实验平台
为验证六位置误差补偿模型对加速度计输出特性的准确反映,采用MPU6050和2TS-450型双轴精密转台进行实验,实验装置如图1和图2所示。
2.1.1 双轴精密转台
在试验中,采用的转台是2TS-450双轴速率位置转台,由江西九江精密试验技术研究所研制。转台具有两个自由度,其双轴位置精度达到±0.000 3°/秒的速率精度,为±0.3″。它的速率范围从0.001°/s覆盖到400°/s,在研究过程中满足了测试要求。
2.1.2 MPU6050
MPU6050是InvenSense公司推出的整合性6轴运动处理组件,它将3轴陀螺仪、3轴加速度计和DMP(数字运动处理)封装在一个4 mm×4 mm×
0.9 mm的小型封装中。它可以通过每帧11 Byte(2 Byte帧头+8 Byte数据+1 Byte校验)的姿态数据与设备寄存器进行通信,并且能够在400 kHz的I2C总线上工作,从而实现高效的姿态传感功能。这个传感器具有小尺寸、低功耗、高精度和高耐震性等特点,使得它非常适用于在空间狭小的环境中采集姿态数据,广泛应用于航空航天、自动驾驶、机器人技术等领域[10]。
2.2 实验结果与分析
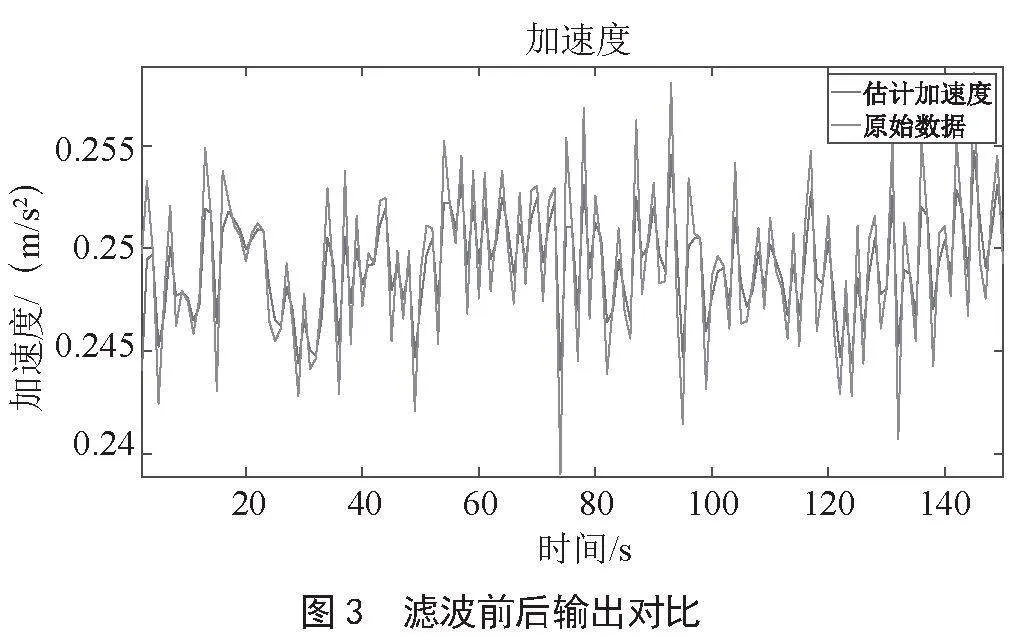
考虑到MEMS加速度计的输出容易受到严重的随机噪声干扰,为提高测量结果的稳定性和精度,在计算标定系数之前采用了卡尔曼滤波对MEMS加速度计的测量值进行了滤波处理。在6个不同位置采集了1分钟的数据测量值,并对这些值进行了滤波处理。图3展示了滤波前后的对比图。
通过卡尔曼滤波处理,有效降低了随机噪声对加速度计输出的影响。这一处理步骤不仅提高了测量结果的稳定性,同时也有助于保持测量精度。图3中的对比清晰展示了滤波前后数据的差异,表明卡尔曼滤波在减弱测量误差方面发挥了显著作用。
这种预处理步骤为后续标定系数的计算提供了更可靠的输入数据,确保了标定过程的准确性。通过减少随机噪声的影响,更可靠地获取MEMS加速度计在不同位置的准确测量值,从而提高了标定结果的可信度。
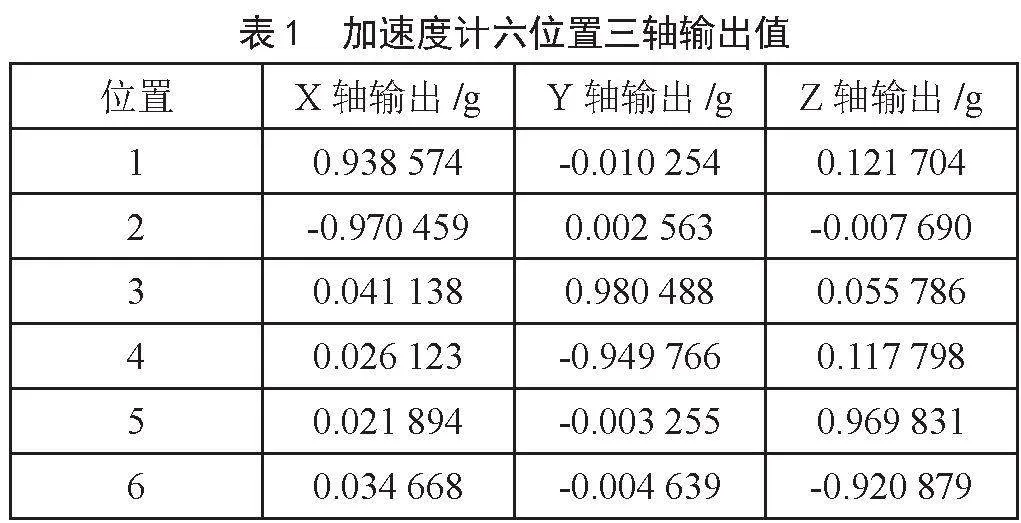
在进行MEMS加速度计数据采集时,采用了6种不同的位置方式,每一种方式下进行了1分钟的静态测量,并计算了相应位置下的平均值,形成了6组加速度计测量数据,具体数据详见表1。接下来,将这些采集的加速度计数据输入六位置误差模型,以获得误差参数矩阵X,并将这些误差参数应用于相应的校正模型,从而获得经过校正后的加速度计输出值。
将加速度计六位置三轴输出值代入式(12)中可求出误差参数矩阵X如下:
将误差参数矩阵X中的值代入式(21)中即可求出加速度计补偿后的输出值:
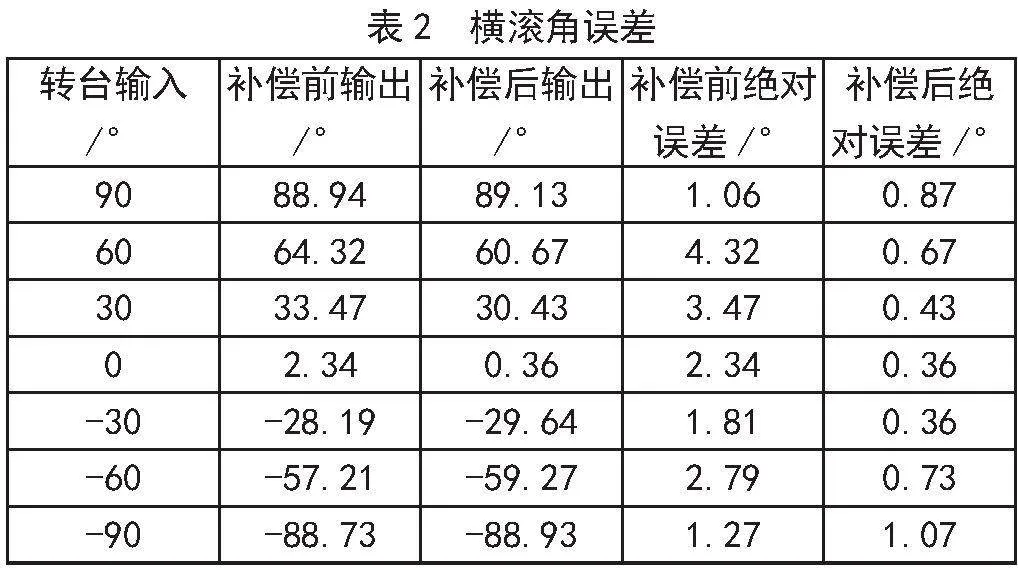
MEMS加速度计的输出数据可用于计算搭载该MEMS-IMU设备的部分姿态角(俯仰角和横滚角)。为验证本文补偿方法的效果,在-90°~+90°范围内逐一设置转台,以横滚角为例,控制设备的横滚角分别为90°,80°,70°,…,0°,-10°,-20°,…,-90°,并记录了经过加速度计补偿前和补偿后的输出值,部分结果如表2所示。从表2可知,经补偿方法后得到的横滚角值更接近实际转台输入的角度。在+90°~-90°范围内,平均绝对误差仅为0.64°。相比之下,在补偿前,平均绝对误差约为2.44°。这进一步证实了补偿方法的有效性和可行性。
3 结 论
尽管MEMS传感器面临较大的误差挑战,但通过采用基于Kalman滤波和六位置法的标定补偿算法,成功提高了MEMS加速度计的测量精度。实验结果清晰地展示,通过补偿处理,MEMS加速度计的输出值更为接近标准值,横滚角的绝对误差也明显减小。本文验证了采用标定补偿算法在提升MEMS加速度计测量精度方面的可行性,并凸显了其在理论和实际工程应用中的价值。成功应用Kalman滤波和六位置法的结合,为克服MEMS传感器误差带来的挑战提供了一种有效而可行的解决方案。
未来的研究方向可以进一步深化该算法,以提升在不同应用场景中的测量准确性和可靠性。可能的改进方向包括对更复杂运动模式和环境条件的适应性增强,以及更为精细的误差模型建立。这样的深化研究将有助于推动MEMS传感器技术在各个领域中的更广泛应用,为实际工程和科学研究提供更为可靠的测量解决方案。
参考文献:
[1] 王淑华.MEMS传感器现状及应用 [J].微纳电子技术,2011,48(8):516-522.
[2] 何昆鹏.MEMS惯性器件参数辨识及系统误差补偿技术 [D].哈尔滨:哈尔滨工程大学,2009.
[3] PODDAR S,KUMAR V,KUMAR A. A Comprehensive Overview of Inertial SeXk9G2BBm5nARyfM2KVL6GF7UcYtjpZFAPe04tcenhlQ=nsor Calibration Techniques [J/OL].Journal of Dynamic Systems, Measurement, and Control,2017,139(1):011006[2023-10-26].https://doi.org/10.1115/1.4034419.
[4] 陈林.低成本MEMS惯性测量组件复合标定与误差补偿方法研究 [D].沈阳:沈阳理工大学,2017.
[5] 于亚云,熊磊.加速度计标度因数的测量不确定度研究 [J].计测技术,2018,38(2):47-49.
[6] 贾继超,王萌,刘鑫,等.一种石英挠性加速度计非线性误差系统级标定方法 [J].中国惯性技术学报,2023,31(1):67-71+79.
[7] 鹿珂珂,刘陵顺,寇昆湖,等.不依赖精密转台的MEMS-IMU误差标定补偿方法 [J].仪器仪表学报,2022,43(4):129-136.
[8] 宋丽君,秦永元.MEMS加速度计的六位置测试法 [J].测控技术,2009(7):11-13+17.
[9] 王学斌,徐建宏,张章.卡尔曼滤波器参数分析与应用方法研究 [J].计算机应用与软件,2012,29(6):212-215.
[10] 朱凯,张艳东.基于MPU6050的高精度钻孔应力计安装杆设计 [J].电子技术与软件工程,2021(10):59-61.