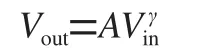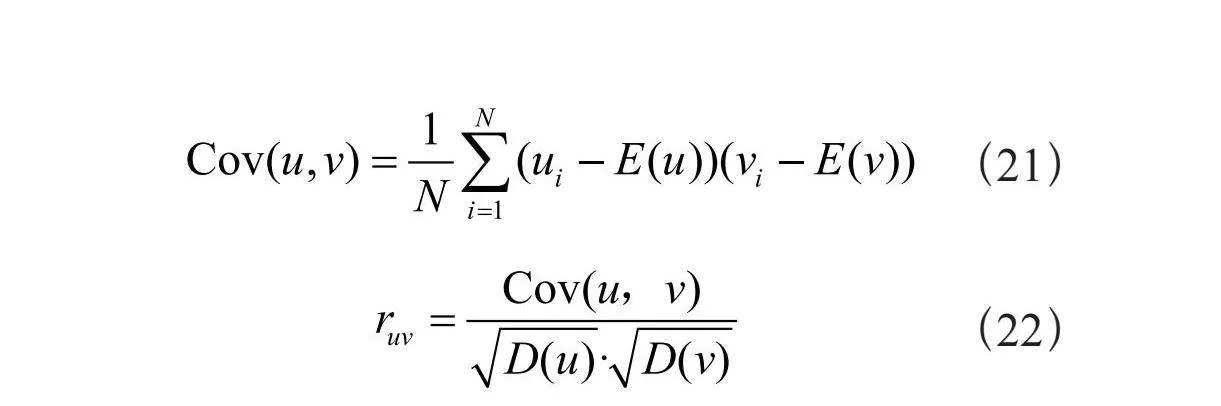




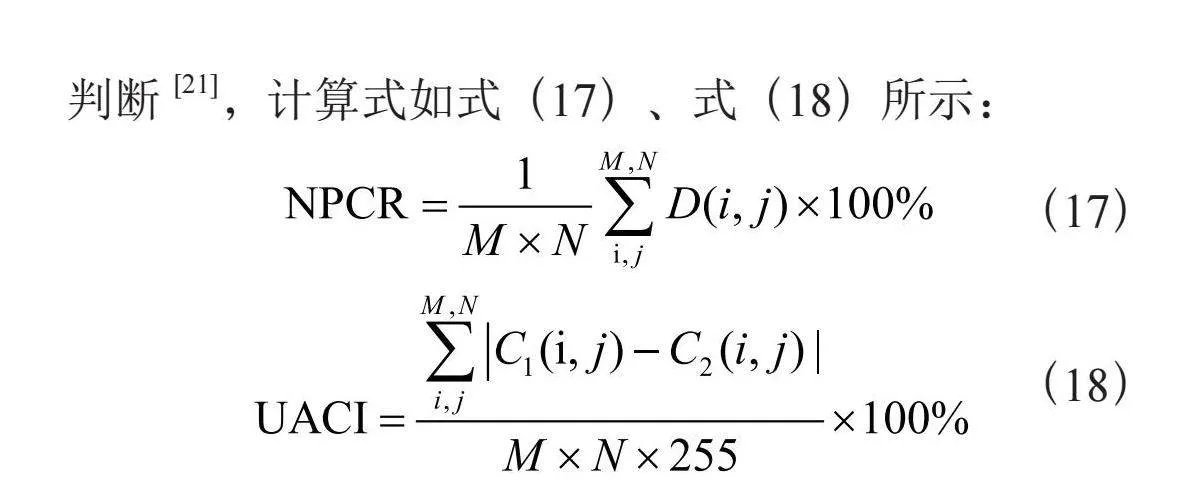







摘 要:图像加密算法研究在确保图像信息安全方面至关重要,图像中包含的信息量较大,相邻像素间存在较强的关联性,在传输过程中容易造成信息泄露。为了打破图像相邻像素间较强的关联性以及提高抗攻击性,提出了基于四维混沌系统DNA编码的彩色图像加密算法。采用四维混沌系统模型产生混沌序列,利用产生的混沌序列和DNA编码等方法对加密图像进行置乱处理,最后对图像加密效果和抗攻击性能进行对比验证。仿真结果表明,通过该算法对图像加密后,相邻像素间的关联性大大削弱。相较于对比算法,该算法能够对彩色明文图像进行有效的加密,同时算法具备抵御干扰和攻击的能力,显著提高了图像的安全性,在彩色图像加密领域具有一定的发展前景。
关键词:图像加密;四维混沌系统;DNA编码;抗攻击性
中图分类号:TP301.6 文献标识码:A 文章编号:2096-4706(2024)15-0142-08
Colour Image Encryption Algorithm Based on 4D Chaotic System
ZHANG Chenglong, ZHANG Chaoxia, LIU Qianwei
(School of Mechatronic Engineering and Automation, Foshan University, Foshan 528225, China)
Abstract: The research on image encryption algorithms is crucial in ensuring image information security. Images contain a large amount of information, and there is strong correlation between adjacent pixels, which can easily cause information leakage during transmission. In order to break the strong correlation between adjacent pixels in images and improve their resistance to attacks, a color image encryption algorithm based on 4D chaotic system DNA encoding is proposed. It uses a 4D chaotic system model to generate chaotic sequences, the encrypted images are scrambled using the generated chaotic sequences and DNA encoding methods. Finally, the image encryption effect and anti-attack capability are compared and verified. The simulation results show that after encrypting the image by using this algorithm, the correlation between adjacent pixels is greatly weakened. Compared to comparative algorithms, this algorithm can effectively encrypt color plaintext images, and has the ability to resist interference and attacks, significantly improving the security of images. It has certain development prospects in the field of color image encryption.
Keywords: image encryption; 4D chaotic system; DNA coding; anti-attack capability
0 引 言
随着互联网的快速发展,人们有了更加便捷的信息交流方式,图像作为一种信息载体,其在我们的日常交流中占据着重要地位。同时用户在使用过程中又面临一系列的信息安全问题,例如图像信息在互联网中传输时怎么保证图像信息的安全。截至目前,多媒体通信领域已采用信息隐藏、图像加密、数字签名、认证、篡改[1-2]等加密技术。数字图像作为一种重要的信息载体,有效保护其中的信息尤为重要,而解决这一问题的关键就是对图像进行加密存储与传输。因此,数字图像传输和存储过程中的信息安全问题也越来越受到广大群众的关注。
由于图像的固有特性,传统加密方法(如国际数据加密算法(IDEA))不能应用于图像信息加密。由一组非线性确定性动力学方程所描述的混沌系统的特性与密码学设计的两个基本原理(扩散和混淆)有关。因此,混沌系统在图像加密中得到了广泛的应用[3-5]。其中,混沌系统的加密方法有两种,分别为一维混沌加密和多维混沌加密。一维混沌映射结构简单,易于实现,且生成混沌序列所需的时间较短。但它也有一些缺点[6-9],如混沌行为的范围很小,李雅普诺夫指数很低。同时因为混沌系统具有错综复杂的相空间和伪随机性等特点,可以用来修改图像的像素位置和像素数值,从而使混沌加密技术在图像加密中得以广泛使用。基于混沌理论的图像加密还能延伸到变换域,例如常见的傅里叶变换、小波变换等。而将变换域加密与空域加密相结合,能进一步增强加密算法的抗攻击性[10-11]。通过变换域加密的图像在解密时都要进行逆变换操作,而经逆变换得到的解密图像相较于原始图像会有一定的信息损失,考虑到人眼对图像失真有比较高的容错性,所以在某些情形下有损的图像加密是可以被接受的。
近年来的研究发现,DNA编码由于可以同时操作图像的像素位置和像素值,在图像加密领域得到了广泛的应用。DNA序列的排列组合并不是唯一的,同时DNA序列还存在着数据存储密度大等优点,因此混沌系统结合DNA编码技术是一个不错的选择。目前国内外许多研究者提出将混沌系统和DNA编码两种方法合二为一的图像加密算法[12]。Wang [13]提出一种基于双混沌和DNA编码技术的图像加密方法。Zhang [14]提出一种基于超混沌和DNA序列的图像加密方法。这些加密方法具有良好的安全性,在图像加密领域得到广泛的应用。因此将混沌系统与DNA编码技术相结合的方案在优化图像加密性能方面是切实可行的。
本文提出一种基于四维混沌系统的彩色图像加密算法,通过实验数据分析得出,本文加密算法具有良好的安全性能,使用场景也比较广泛。
1 基本理论
1.1 小波变换
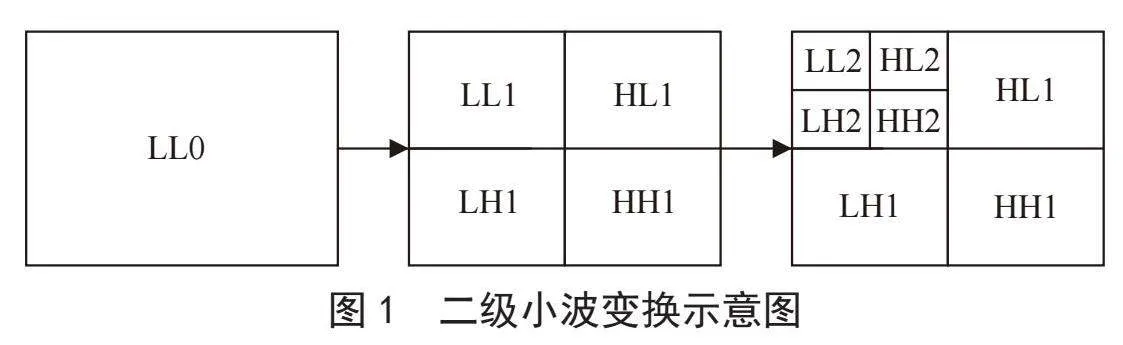
这里采用Mallet算法对大小为512×512的原始灰度图像I进行第一次小波变换分解,经过第一次小波变换分解后得到4个大小为256×256的子块图像,分别为低频近似分量LL、水平高频细节分量HL、垂直高频细节分量LH及对角高频细节分量HH,其中低频信号存储着原文图像的主要信息。因此,可以对低频部分多次应用小波变换,将L1分解为L2,H2,将L2分解为L3,H3,…,依此类推,可以获得多个层次上的信号分量。本文对原始图像进行两次小波变换,图1为二级小波变换示意图。
在本文中,采用二维连续小波变换的方法。二维连续小波变换表达式如式(1)所示:
(1)
1.2 DNA基本理论
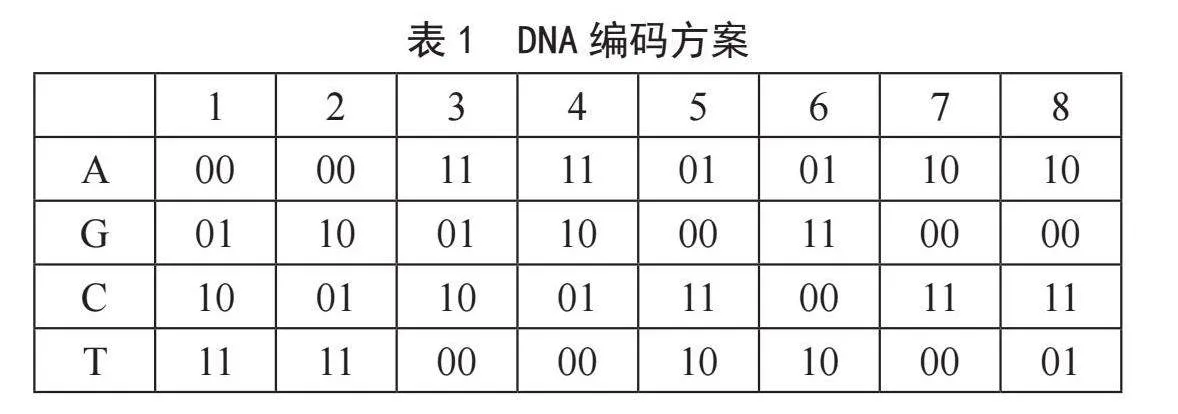
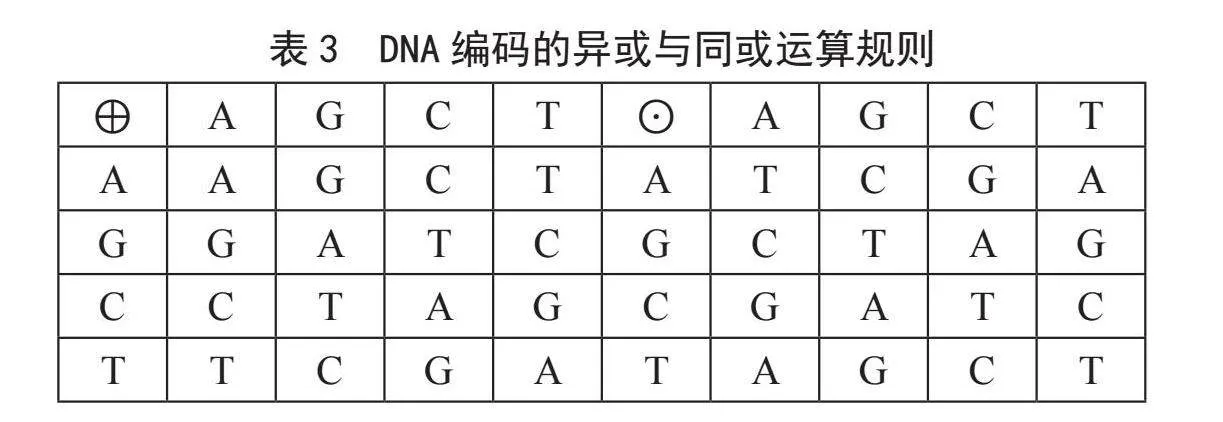
在生物学中,每条DNA分子链都会包含A、C、G、T四种核酸碱基,按照配对规则A与T配对,C与G配对[15]。A、C、G、T四个碱基编码分别采用00、01、10、11的方式进行DNA编码,根据这种编码组合方式组合的结果有24种,其中符合Watson-Crick规则的仅有8种,编码组合如表1所示。
1.3 DNA运算规则
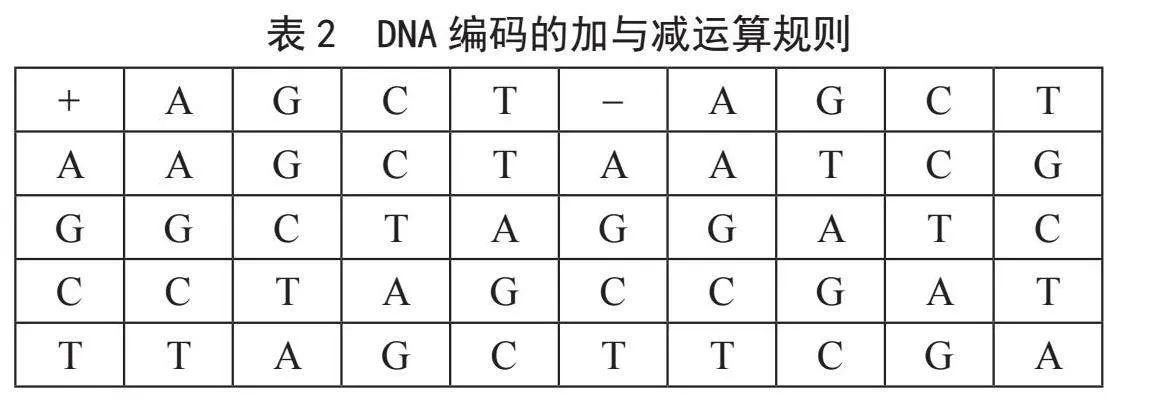
对于满足DNA编码规则的这8种编码方式,每种编码方式都有自己的运算规则,分别是加法、减法、同或、异或四种DNA编码运算规则。本文定义的DNA运算规则如式(2)所示:
(2)
当a = 0时,取用DNA的加运算;当a = 1时,取用DNA的减运算;当a = 2时,取用DNA的异或运算;当a = 3时,取用DNA的同或运算。表2和表3分别介绍了DNA编码的4种运算规则。
1.4 Logistics映射
Logistic混沌映射是加密体系中最常用到的一个系统,同时它也是一种经典的一维混沌映射,起源于虫口模型,其表达式如式(3)所示:
(3)
其中,μ为分支参数,Xn为得到的混沌序列。研究表明,当μ ∈ [3.569 945 627 4]时,序列Xn处于混沌状态[16]。
1.5 Zigzag变换
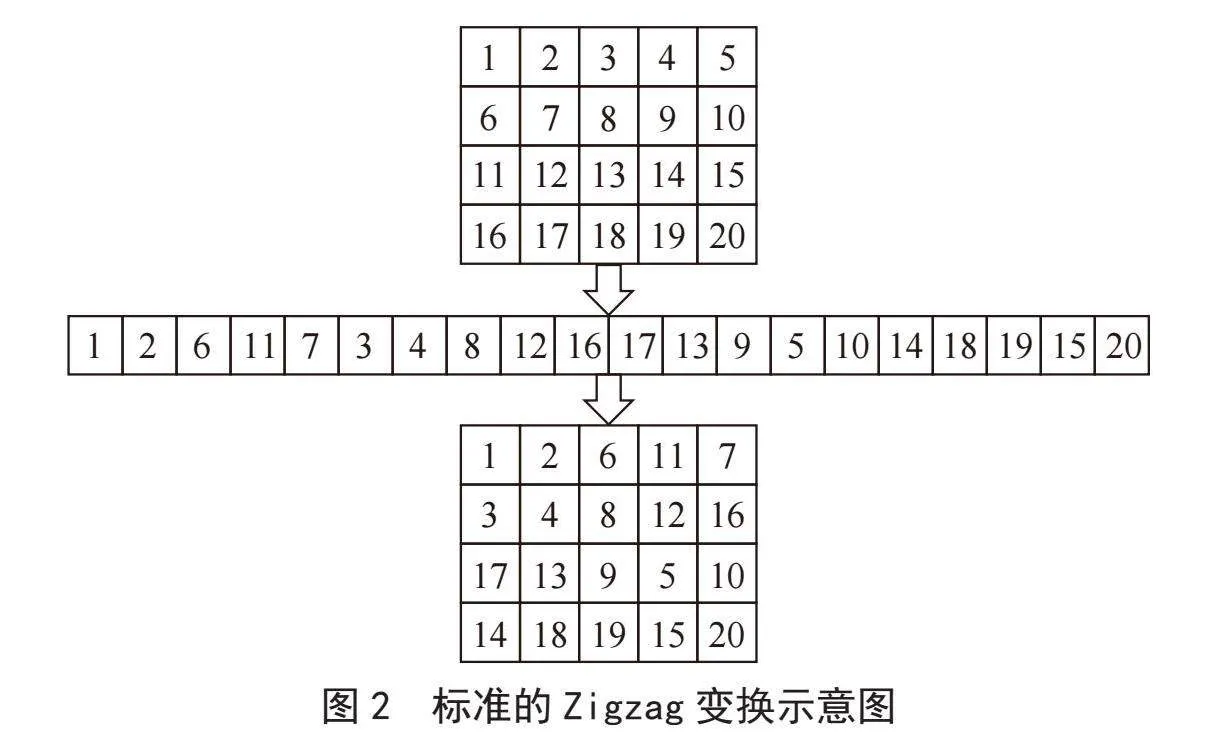
Zigzag变换[17]是一种常用置乱方法,其本质是元素之间的互换。Zigzag变换即从矩阵左上角开始按“之”字形对矩阵中的每一个元素进行遍历,按照遍历元素的顺序排列成一个一维矩阵,随后按一定的规则将一维矩阵转变为二维矩阵。同理,采用Zigzag的反变换规则进行Zigzag反置乱,即可将Zigzag置乱后的矩阵复原。Zigzag变换过程以5×4的矩阵为例,变换过程如图2所示。
2 混沌系统
四维混沌系统方程如式(4)所示:
(4)
其中,a = 20,b = 80,c = 10,d = 560,e = 5,f = 0.5,g = 0.1。
2.1 Lyapunov指数分析
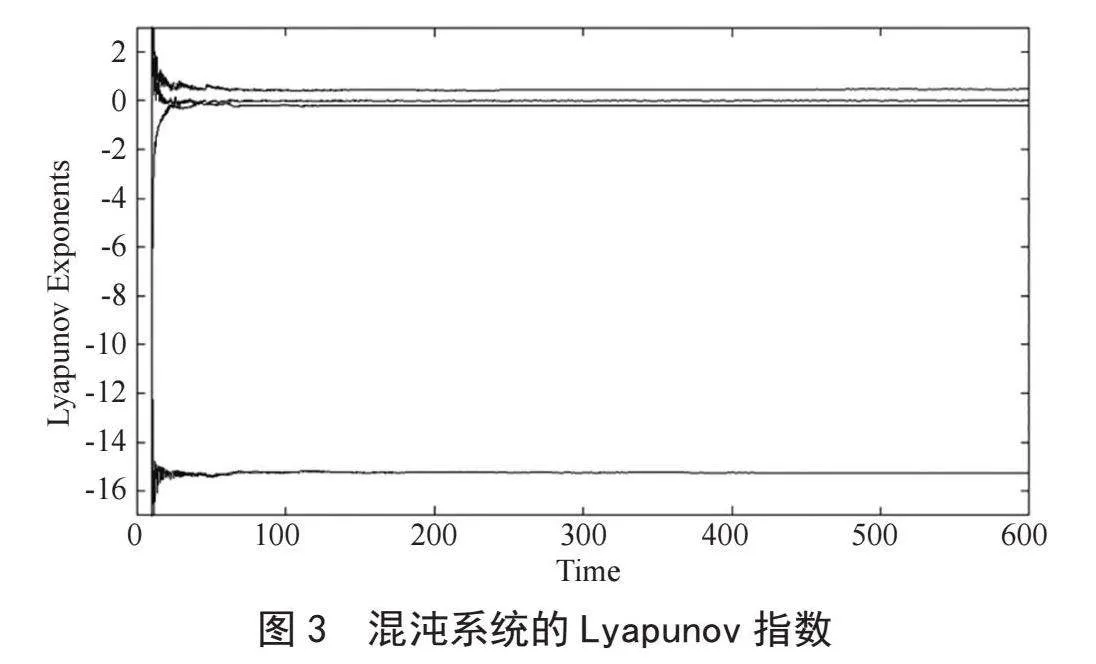
新构造的四维系统是否具有混沌特性,主要通过Lyapunov指数的计算来分析。当系统参数a = 20,b = 80,c = 10,d = 560,e = 5,f = 0.5,g = 0.1时,该系统的Lyapunov指数如图3所示。从图3中可以看出,有一个正的Lyapunov指数,为0.467,有一个为零的Lyapunov指数,有两个负的Lyapunov指数,分别为-0.206和-15.255,因此该系统处于混沌状态。
2.2 平衡点分析
令 = = = = 0,即:
(5)
(6)
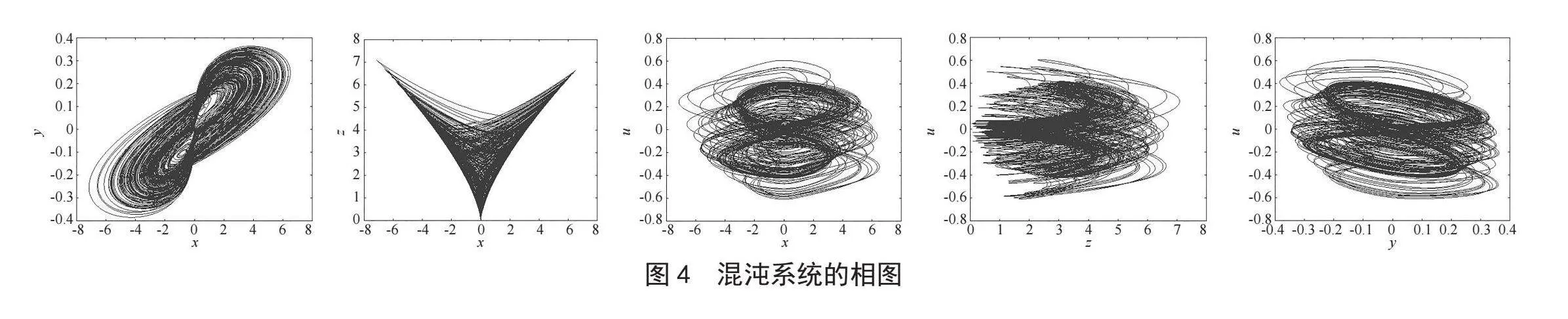
2.3 四维混沌系统的相图
当系统参数为a = 20,b = 80,c = 10,d = 560,e = 5,f = 0.5,g = 0.1时,系统产生的四维相图如图4所示。
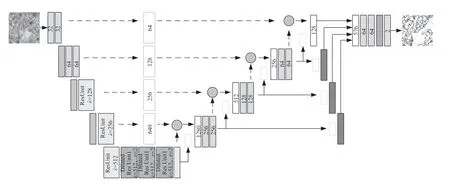
3 基于四维混沌模型的图像加密算法
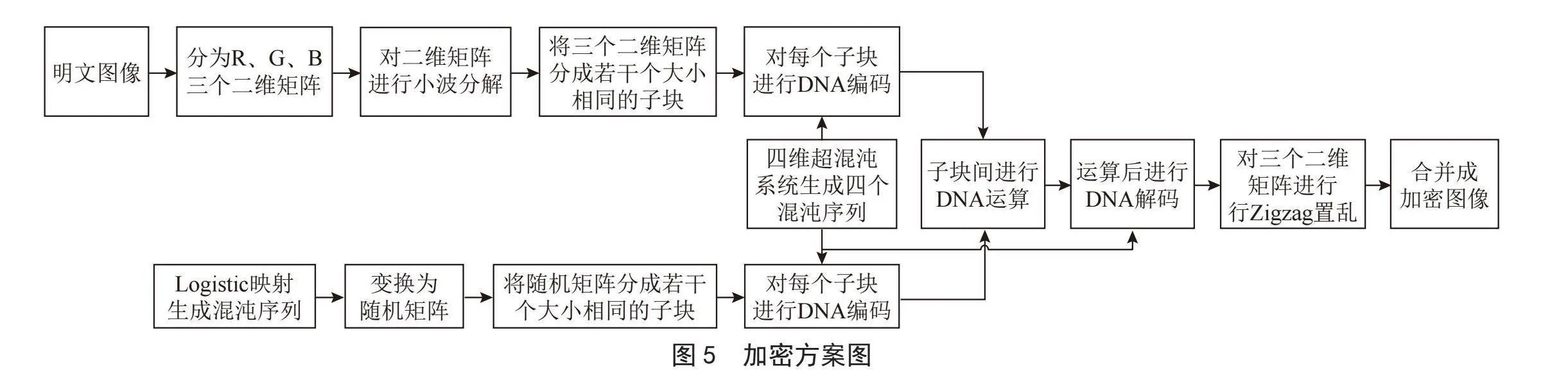
总体加密方案图如图5所示,该方案将彩色数字图像分为RGB三个二维矩阵,对每个二维码矩阵进行两次小波变换,随后分块进行DNA编码和运算,利用四维混沌系统方程生成随机序列进行DNA编码,加密后进行Zigzag置乱,最后合并三个通道得到彩色加密图像。
详细的加密步骤如下:
1)按照式(7)将彩色图像I分为R、G、B三个二维矩阵,称为I1、I2、I3。
(7)
2)将I1、I2、I3三个二维矩阵进行两次小波变换。
(8)
其中,I1_CA_2为第一次小波变换的低频部分,主要信息都集中在低频段,可以再次对低频段进行小波变换,这里将以广泛应用的哈尔小波作为小波基。
3)设定初值X0和参数μ。根据式(3)对Logistic映射连续迭代得到序列{ki},其中μ设定为3.999 9,作为加密时的密钥之一。由此可获得混沌序列,初值X0根据式(9)产生:
(9)
4)按式(10)将序列{Ki}转换为与I1大小相同的M×N二维矩阵,并将矩阵的值转化为0至255的范围内进行DNA运算:
(10)
5)设定好初值和参数后,利用MATLAB内置的龙格-库塔函数ode45计算四维混沌系统的初值,得到四个长度均为(M×N) / t2的序列{Xi}、{Yi}、{Zi}、{Hi}。四维混沌系统的四个初值X(0)、Y(0)、Z(0)、H(0)由式(11)计算得出:
(11)
6)DNA编码共有8种方式,因此需要将序列{Xi}和序列{Yi}的值转化为1至8范围内的整数。按式(12)将{Xi}和{Yi}序列进行转化:
(12)
转化后的序列{Xi}的值为1到8之间的随机整数,I1、I2、I3中第i个子块的DNA编码方式为Xi,混沌矩阵R中第i个子块的DNA编码方式为Yi。
7)本算法中共采用四种DNA运算法则,所以需要按式(13)将序列{Zi}进行变换,转化为0到3范围内的整数:
(13)
8)对经过DNA运算后的矩阵分块进行DNA解码。DNA解码过程实则为DNA编码的逆过程,DNA解码即将A、G、C、T解码成具体的数值,同时DNA解码规则仍然是由序列{Hi}决定的。
9)获得两个Logistic混沌序列。其中,μ统一设定为3.999 9,两个初值X01和X02根据式(14)产生:
(14)
其中,X01为待加密图像R通道与B通道的灰度平均值,X02为G通道与B通道的灰度平均值,X01和X02的值随图像而变化,因此作为此加密算法的密钥。
10)根据式(15)将经过DNA解码后的I1、I2、I3三个二维矩阵进行Zigzag置乱。此步骤主要是提升密文图像抗裁剪攻击的能力。
(15)
11)将经过Zigzag置换的三个二维矩阵合并为一个三维矩阵,得到密文图像。
4 实验测试
实验选取Lena和Pepper两幅彩色图像进行测试验证,大小均为512×512,加解密图像效果如图6所示。
5 安全性分析
5.1 密钥空间分析
密钥空间的大小是评价一个图像加密算法性能的重要因素之一。本文使用了Logistic混沌系统和四维混沌系统,混沌系统的初值用精确到小数点后15位的浮点数表示,其中μ、X0,系统参数a、b、c、d、e、f、g及四维混沌系统参数X(0)、Y(0)、Z(0)、H(0)作为密钥,此加密算法的密钥容量为10195。如果一种图像加密算法的密钥空间大于2100,那么它就是安全的[18]。本算法的密钥空间远大于2100,因此本算法足够安全。
5.2 直方图分析
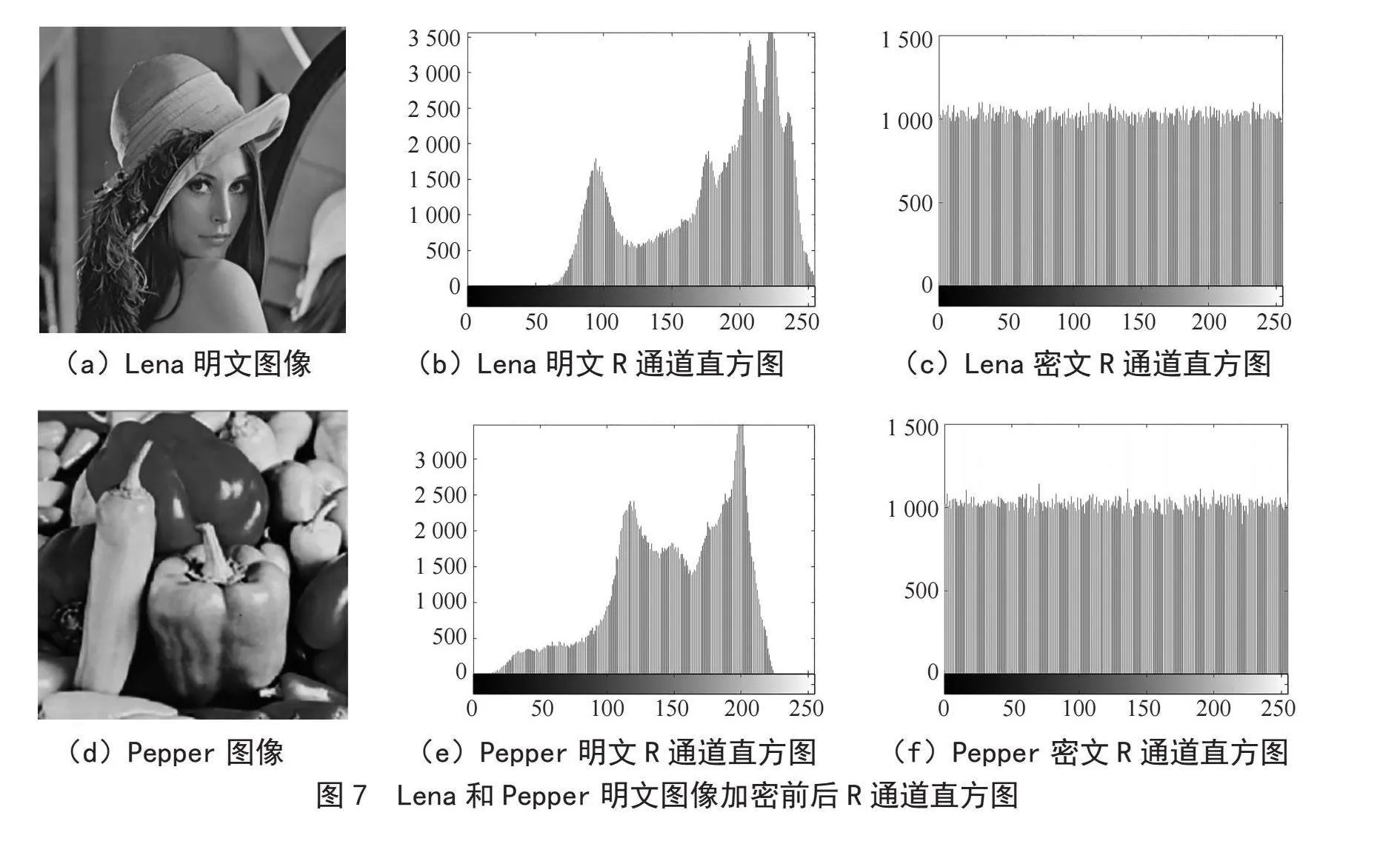
在图像直方图当中,直方图的纵坐标趋势越平坦,表示整个图像的像素值分布越均匀[19]。因此我们可以通过直方图清楚了解加密前后图像像素值的分布情况。图7分别是Lena和Pepper明文图像加密前后R通道直方图。
5.3 信息熵分析
信息熵反映一个系统中信息的混乱程度[20],计算式如式(16)所示:
(16)
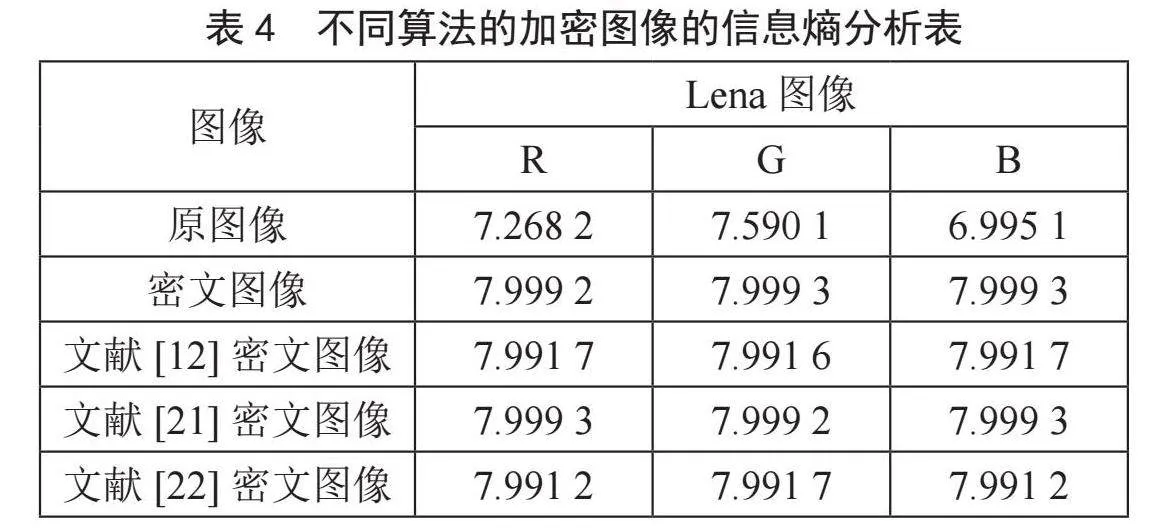
其中,p(mi)为图像当中灰度值所占比例,L为图像的灰度级。灰度图像其信息熵的理论计算最大值为8。本文中采用Lena图像作为实验图像,本文图像加密后的信息熵与文献资料[12,21,22]加密后图像的信息熵进行对比,结果如表4所示。由表5可知该算法能够有效地对图像信息进行打乱,具有良好的加密效果。
5.4 抗差分攻击能力分析
差分攻击是通过输入不同数据来查看对输出影响的攻击,一个合格的加密算法需要能抵御差分攻击。抵御差分攻击的能力主要是通过像素变化率(NPCR)和归一化平均变化强度(UACI)这两个性能指标来判断[21],计算式如式(17)、式(18)所示:
(17)
(18)
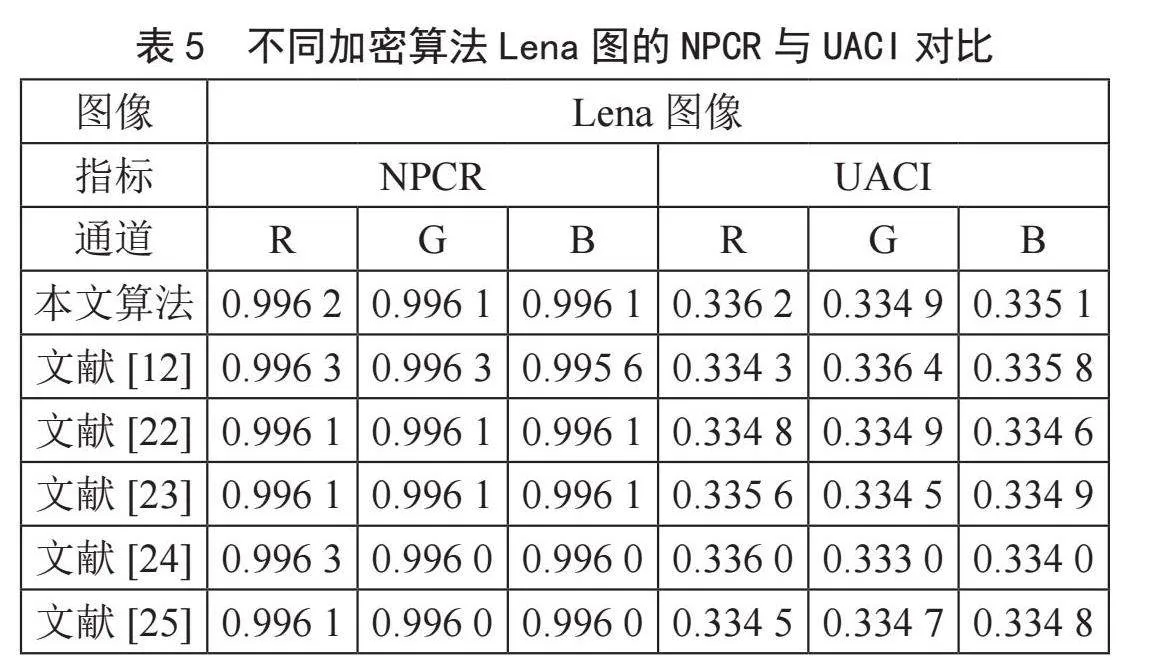
其中,M、N分别为图像矩阵D的行和列,K1(i,j)为原始图像改变一个像素点加密后密文的像素值,K2(i,j)为原始图像加密后密文的像素值。本文将原始图像的第一个像素减1,得到一个改变后的图像,再对改变后的图像进行加密。随后再对原始图像进行加密,这样就得到两个密文图像并对它们进行测试。NPCR和UACI的数值越大,说明原始图像与解密后图像的差异越大。从表5可以看出,相比于其他文献的NPCR和UACI性能指标,本文算法的密钥敏感性更强,能够有效抵御差分攻击。因此提出的加密算法具有良好的密钥敏感性。
5.5 相邻位置数据值关联性分析
图像相邻位置像素值往往与抗攻击性能有着密切关系,通常来说,图像相邻位置关联性越强,则其抵御攻击的能力就越弱[18]。本文按照式(19)至式(22)对明密文图像的水平、垂直和对角线三个方向的相关性系数ruv进行计算:
(19)
(20)
(21)
(22)
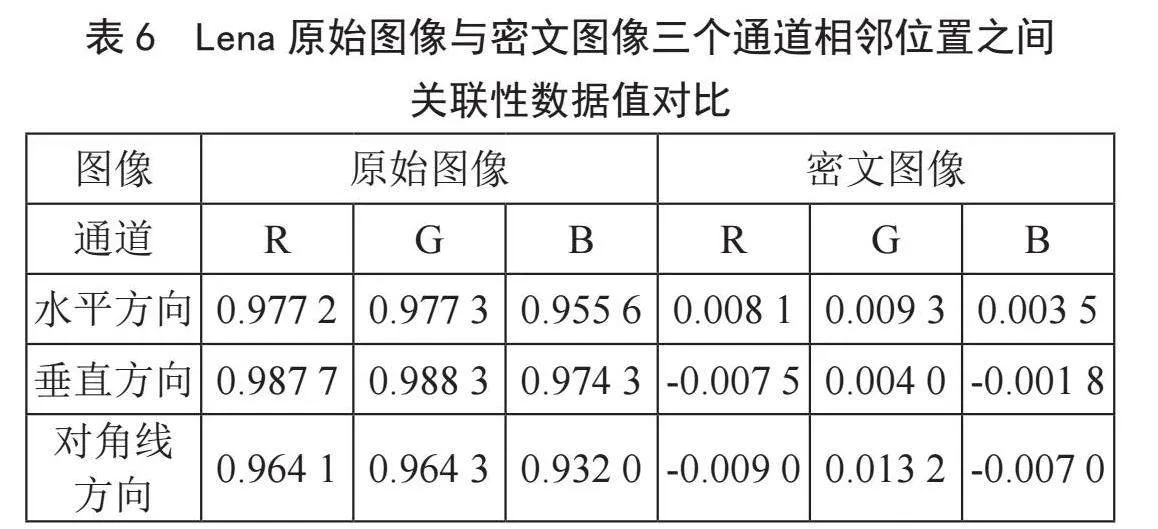
其中,u和v为相邻位置的数据值,N为所取像素点对数5 000,E(u)为N个像素点的平均值,D(u)为N个像素点的方差,Cov(u,v)为相关函数,ruv为随机变量u和v的相关系数,其绝对值越大,表示关联性越强。表6为Lena原始图像与密文图像三个通道相邻位置之间关联性的数据值对比。
可以看出,原始图像三个通道的相关性系数都趋近于1,表明其相邻位置的关联性很大,而经过本文的加密算法后相邻位置关联性接近于0。通过与文献中的数据对比,经过本文算法加密的图像效果更好一些。
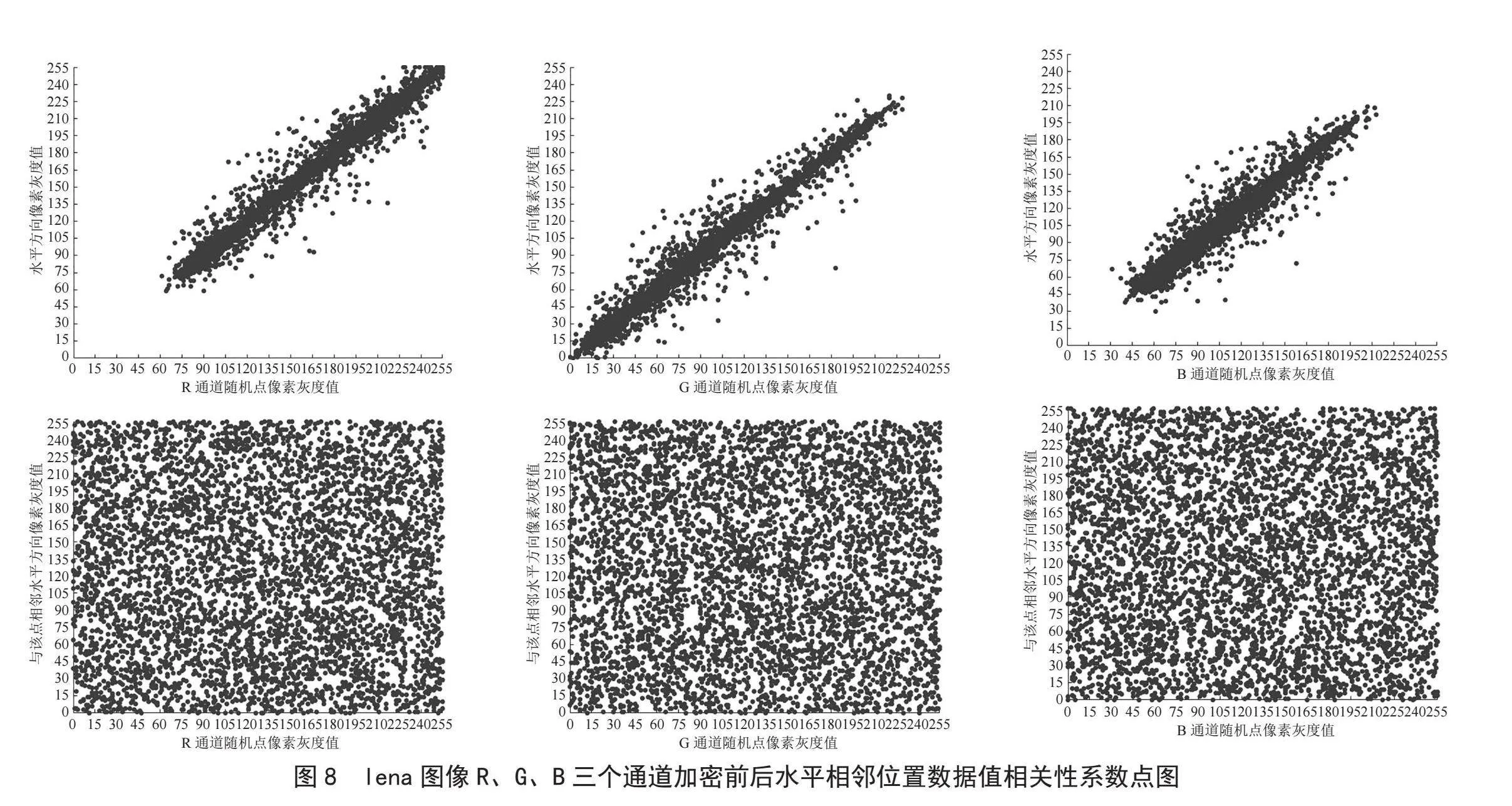
通过图8中6张相关性系数点图可以看出,明文图像三个通道水平相邻位置的数据值关联性都很强,数据点分布呈线性关系。而密文图像水平相邻位置数据值之间的关联性几乎为0,数据点分布完全随机,说明此加密算法完全改变和打乱了原图的像素点数值和位置,拥有较强的抗攻击能力。
5.6 抗剪切能力分析
当密文图像在传输过程中受到裁剪攻击时,需要尽可能保留图像当中的基本信息。这里将在Lena的密文图像当中剪掉一块大小为50×50的区域,随后对经过裁剪的密文图像进行解密。从图9中可以看出,虽然经过解密后原始图像部分像素值发生丢失,但它依然能还原原始图像的基本信息,说明该加密算法具有一定的抗剪切能力。
5.7 抗噪声能力分析
在图像的传播过程中常常会受到通道噪声的影响。本文对加密后的Lena密文图像分别加入0.05和0.15的椒盐噪声来模拟传输过程受到干扰的情形。从图10中可以看出,虽然密文图像受到椒盐噪声的干扰导致部分像素值发生了改变,但通过解密依然能还原图像的基本信息,因此本算法具有一定的抗噪声能力。
6 结 论
针对目前图像加密算法存在的不足,以改善图像加密效果为目标,提出一种基于四维混沌系统的彩色数字图像加密算法,并与经典的图像加密算法进行对比。通过实验得到加密算法加密前后的直方图、信息熵、相邻像素之间相关性等一系列图像评价指标,表明引入四维混沌系统模型能对图像进行有效的置乱处理,扩大密钥空间,大幅减弱原始图像和加密后图像之间的相关性,进而能够抵抗几种常见的攻击。同时该算法简单易用,加解密时间短,满足图像安全性分析的实时性需要,表明本文的加密算法可应用到彩色图像的加密。
参考文献:
[1] PAK C,HUANG L L. A New Color Image Encryption Using Combination of the 1D Chaotic Map [J].Signal Processing,2017,138:129-137.
[2] ZENATI A,OUARDA W,ALIMI A M. A New Digital Steganography System Based on Hiding Online Signature within Document Image Data in YUV Color Space [J].Multimedia Tools and Applications,2021,80:1-24.
[3] HAO J,MOU J,XIONG L,et al. A Novel Color Image Encryption Algorithm Based on the Fractional Order Laser Chaotic System and the DNA Mutation Principle [J/OL].Multimedia Tools and Applications,2022,81(1)[2023-11-16].https://www.researchgate.net/publication/354597060_A_novel_color_image_encryption_algorithm_based_on_the_fractional_order_laser_chaotic_system_and_the_DNA_mutation_principle.
[4] HAMDI M,MIRI J,MOALLA B. Hybrid Encryption Algorithm (HEA) Based on Chaotic System [J].Soft Computing,2020,25(3):1847-1858.
[5] MUSANNA F,DANGWAL D,KUMAR S. Novel Image Encryption Algorithm Using Fractional Chaos and Cellular Neural Network [J].Journal of Ambient Intelligence and Humanizd Computing,2022,13:2205-2226.
[6] YANG T,YANG L B. Breaking Chaotic Switching Using Generalized Synchronization: Examples [J].IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications,1998,45(10):1062-1067.
[7] AKHSHANI A,AKHAVAN A,LIM S C,et al. An Image Encryption Scheme Based on Quantum Logistic Map [J].Communications in Nonlinear Science and Numerical Simulation,2012,17(12):4653-4661.
[8] WANG B,WEI X P,ZHANG Q. Cryptanalysis of an Image Cryptosystem Based on Logistic Map [J].Optik,2013,124(14):1773-1776.
[9] NKANDEU Y P K N,PONE J R M,TIEDEU A. Image Encryption Algorithm Based on Synchronized Parallel Diffusion and New Combinations of 1D Discrete Maps [J/OL].Sensing and Imaging,2020,21(1)[2023-11-09].https://link.springer.com/article/10.1007/s11220-020-00318-y.
[10] ZHANG X,YE R S. A Novel RGB Image Encryption Algorithm Based on DNA Sequences and Chaos [J].Multimedia Tools and Applications,2021,80:8809-8833.
[11] CHAI X L,GAN Z H,CHEN Y R,et al. A Visually Secure Image Encryption Scheme Based on Compressive Sensing [J].Signal Processing,2017,134:35-51.
[12] 杨吉云,吴昊.基于混沌系统和动态DNA编码与运算的彩色图像加密算法 [J].计算机工程,2018,44(2):151-157.
[13] WANG X Y,GAO S. Image Encryption Algorithm for Synchronously Updating Boolean Networks Based on Matrix Semi-tensor Product Theory [J].Information Sciences,2020,507:16-36.
[14] ZHANG X,YE R S. A Novel RGB Image Encryption Algorithm Based on DNA Sequences and Chaos [J].Multimedia Tools and ApU59Muhp4jLIx3b8wr0AVNDeAvDQ5RxS7+0MxLAUPb04=plications,2020,80(6):8809-8833.
[15] 杜鑫昌,高瑜翔,曹远杰,等.基于混沌压缩感知和DNA编码的多图像加密算法 [J].无线电工程,2022,52(3):476-483.
[16] 韦丞婧,李国东.结合超混沌系统和Logistic映射的视频图像加密算法 [J].计算机工程,2022,48(5):263-271.
[17] 刘艮,蒋天发,蒋巍.一种基于Zigzag变换的彩色图像置乱算法 [J].计算机工程与科学,2013,35(5):106-111.
[18] 庄志本,李军,刘静漪,等.基于新的五维多环多翼超混沌系统的图像加密算法[J].物理学报,2020,69(4):50-63.
[19] 司宇晨,滕琳,孟娟.随机弹射结合DNA编码的图像加密算法 [J].软件导刊,2021,20(8):185-190.
[20] 邓文博,刘帅,刘福才,等.基于压缩感知和DNA编码的图像加密算法 [J].计算机工程与科学,2022,44(9):1574-1582.
[21] 张淑霞,李珊珊,白牡丹,等.基于混沌系统的数字彩色图像加密技术 [J].科学技术与工程,2022,22(13):5291-5298.
[22] 张赛男,李千目.一种基于Logistic-Sine-Cosine映射的彩色图像加密算法 [J].计算机科学,2022,49(1):353-358.
[23] REHMAN A U,LIAO X F,ASHRAF R,et al. A Color Image Encryption Technique Using Exclusive-OR with DNA Complementary Rules Based on Chaos Theory and SHA-2 [J].Optik,2018,159:348-367.
[24] WANG X Y,ZHANG H L,BAO X M. Color Image Encryption Scheme Using CML and DNA Sequence Operations [J].Biosystems,2016,144:18-26.
[25] KADIR A,AILI M,SATTAR M. Color Image Encryption Scheme Using Coupled Hyper Chaotic System with Multiple Impulse Injections [J].Optik,2017,129:231-238.
作者简介:张成龙(1997—),男,汉族,广东茂名人,硕士研究生在读,研究方向:计算机图像处理;通讯作者:张朝霞(1976—),女,汉族,广东佛山人,副教授,博士,研究方向:计算机图像处理;刘芊伟(2000—),男,汉族,江西上饶人,硕士研究生在读,研究方向:计算机图像处理。