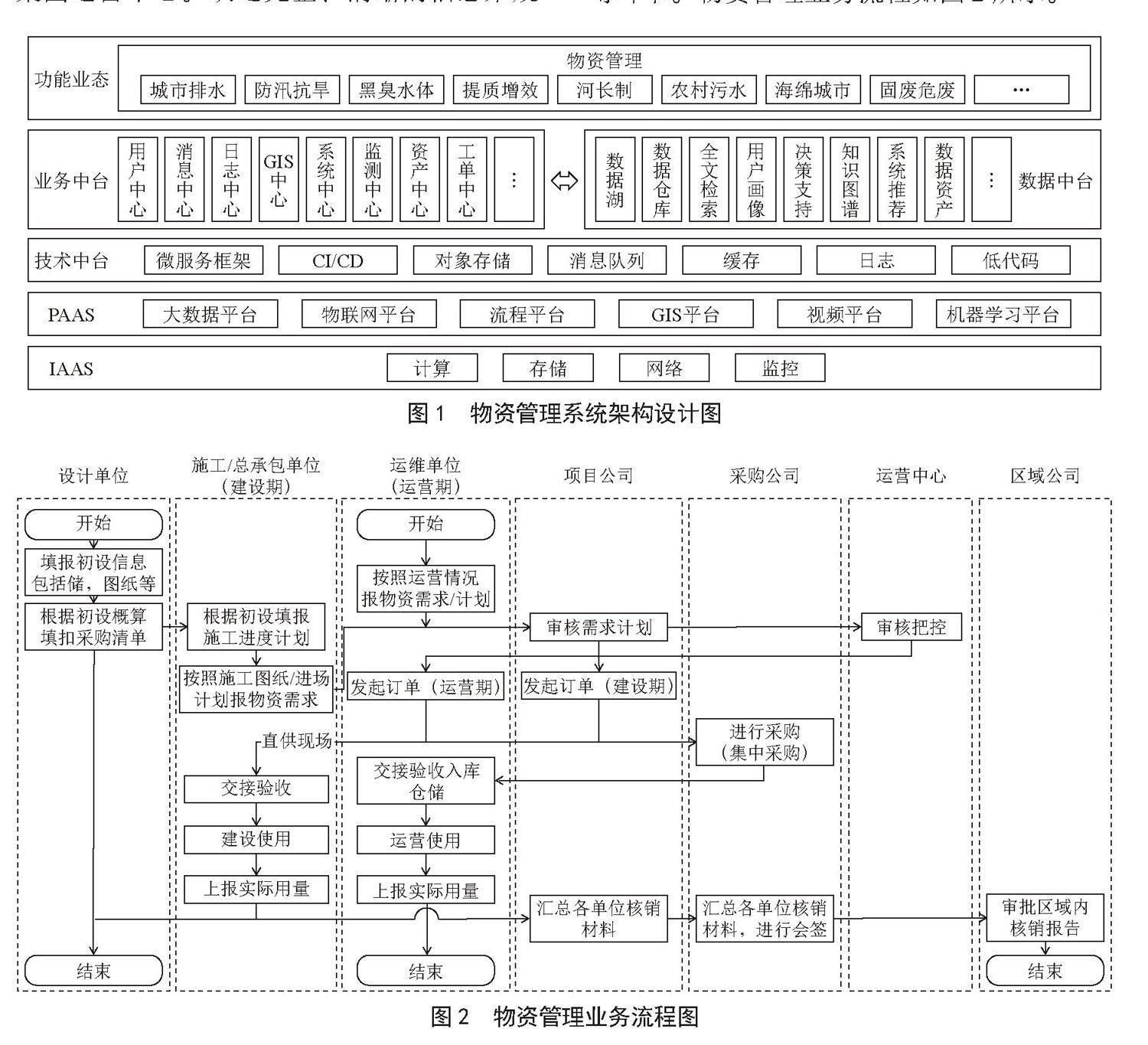




摘 要:文章基于LSTM模型预测感染人数,构建了物资需求模型,推导出应急仓库订货数量。文章首先从应急物资分类入手,为构建订货模型铺垫。然后,针对预测感染人数这一问题的特点选定LSTM作为预测模型,并搭建LSTM模型网络。最后综合各方面影响因素,建立订货数量计算公式。文章提供了重大突发公共卫生事件下单周期应急仓库订货数量量化方法,为应急物资供应链仓储订货提供了科学的数据支撑。
关键词:应急仓库订货;应急物资;LSTM模型;感染人数预测
中图分类号:TP391 文献标识码:A 文章编号:2096-4706(2024)17-0134-06
0 引 言
应急仓库订货是指在突发公共卫生事件或其他紧急情况下,为了有效地应对灾害或紧急情况,准备和储备必要的物资和资源。在面临突发事件时,快速、准确地补给所需物资对于保障人员安全和救治工作的顺利进行至关重要。通过科学的数量设定,可以确保应急仓库中始终保持足够的储备物资,以应对各种突发情况,保障社会的安全和稳定
目前仓储领域的研究主要集中在仓库补货问题,对于研究订货数量可以作为参考。Baller等[1]提出一个动态需求联合补货模型(DJRP),将传统的DJRP扩展为考虑运输成本的DJRP(DJRP-AT)。Braglia等[2]提出具有随机需求和缺货-丢失销售混合周期审查联合补货问题,使用极小极大分布无关方法应对缺乏有关需求分布完整信息的情况。Chen等[3]提出一种带有短缺和部分需求代替的联合补货问题(JRP),以预算、运输能力和装运要求等为约束条件构建模型算法。Wang等[4]将传统的模糊模拟(FS)方法和差分进化算法(DE)相结合,提出具有模糊次要补货成本和模糊库存持有的联合补货模型(JRP)。
在应急仓库订货数量确定过程中,受多方面因素影响,主要包括物资需求预测、仓库储存成本以及物资运输成本。在重大突发公共卫生事件中,物资需求预测主要体现在感染人数的预测上。因此,文章研究首先聚焦于重大突发公共卫生事件中感染人数的预测问题。随后就是将储存成本和交通成本考虑其中,构建出订货模型。最后,选取某地区作为案例,利用现有资料查询相关数据,计算验证模型。
1 前期相关研究
1.1 重大突发公共卫生事件下应急物资分类
应急物资是指为了应对用于应急突发事件所需的各种物资,涵盖了应急救援演练、灾后恢复、医疗救治等各个环节所需的基础保障设施、生活救援物资以及生命救助物资等[5]。国家发展和改革委员会主任急物资的分类,应急物资按照用途分类可分为13类,即防护用品类、生命救助类、生命支持类、救援运载类、临时食宿类、污染清理类、动力燃料类、工程设备类、器材工具类、照明设备类、通信广播类、交通运输类、工程材料类[6]。
重大突发公共卫生事件具有严重性、复杂性、不确定性、传播性、阶段性和持续性等特点。由于其严重性,会导致大量病患,因此需要充足的疫苗、药品和医疗消耗器材等。传播性使得医疗工作者和公众都需要大量医疗防护用品。事件的复杂性和阶段性不仅涉及医疗领域,还涉及社会治安等方面,需要为隔离区域的居民提供必要的生活物资。重大突发公共卫生事件存在几个阶段:初期阶段、爆发阶段、相持阶段和恢复阶段[7]。从事件的不同阶段来看,初期阶段传播速度快,病情难以控制,因此需要大量药品,特别是消毒杀菌类药品的需求会急剧增加。爆发阶段感染人数激增,需求进一步增加,消毒杀菌类药品和医疗防护用品的需求急剧上升,同时需要保障隔离区的正常生活物资供应。相持阶段疫情得到控制,但仍需消毒杀菌类药品和医疗防护用品,同时需要继续保持隔离区的物资供应。恢复阶段感染人数逐渐减少,各类物资需求量下降,居民生活逐渐恢复正常。
综合上述分析,在重大突发公共卫生事件下,所需的应急物资种类可大致可分为两类,一类为医疗处置及救护物资,另一类为基本生活保障物资两大类。医疗处置及救护物资又细分救治药品、救治物品和消杀物资。 根据《应急保障重点物资分类目录》,常见的医疗处置及救护物资有抗病毒药物、抗生素、止痛药、消炎药、呼吸机、心电监护仪、口罩、防护服、护目镜、酒精等;常见的基本生活保障物资有棉被、饮用水方便食品等。
1.2 感染人数预测
对于重大突发公共卫生事件的物资需求预测,主要体现在对感染人数的预测。近几年基于循环神经网络(RNN)的深度学习模型被广泛应用,其中具有代表性的为长短期记忆网络(Long Short-Term Memory, LSTM)。LSTM擅长处理时间序列数据,能够捕捉感染人数随时间变化的规律。其灵活的时间间隔处理能力使其适用于不同时间尺度下的数据模式学习。此外,LSTM能够处理复杂的非线性关系,更准确地预测感染人数的变化趋势。通过门控单元的设计,LSTM具有优秀的长期记忆能力,能够有效保留过去较长时间内的信息,从而提高对未来感染人数走势的预测准确性和可靠性。Shahid等[8]等人评估了自回归综合移动平均(ARIMA)、支持向量回归(SVR)、长短期记忆(LSTM)、双向长短期记忆(Bi-LSTM)在内的预测模型,得出测试结果排名顺序为Bi-LSTM、LSTM、GRU、SVR和ARIMA。综合考虑模型计算速度以及模型性能,本文将采用LSTM模型进行感染人数预测。
1.2.1 LSTM模型结构
LSTM结构如图1所示,LSTM通过三个门,即遗忘门、输入门、输出门控制信息量的传入过程,并通过引入“记忆细胞状态”对其进行长期保存[9]。
图1中,ft为遗忘门的控制函数,如式(1)所示。Wf为遗忘门染疫人数实际值的权重矩阵,ht-1隐藏层为前一天的染疫情预测值,bf为遗忘门偏差向量。参数it为输入门的控制函数,与ft类似,通过改变权重矩阵的值用于对新输入的新冠染疫数据进行选择,以避免相关性较低的数据数值加入记忆细胞,如式(2)所示,其中,Wi为输入门新冠染疫真实值的权重矩阵,ht-1为上一时刻隐藏层状态,[ht-1,xt]为两个向量连接成的长向量,bi为输入门偏差向量[10]。
(1)
(2)
对当前时刻新冠染疫数据向量进行处理,该时刻记忆细胞的存储向量是将上一时刻的存储向量和当前时刻新输入的染疫数据向量分别与遗忘门控制函数向量、输入门控制函数向量进行逐元素相乘,进而实现对较长时间的染疫数据信息的记忆存储,Ct用来更新细胞状态,即对相关性较强的历史染疫数据进行记忆,该变量通过舍弃前一天的部分记忆,将新的候选值变量加入记忆,以此不断更新与存储[10],如式(3)、式(4)所示。式(4)中⊙为向量元素乘法运算符号, 为当前时刻染疫情实际值的tanh函数转换值,作为当前时刻染疫情况向量,Wc为当前时刻染疫情况看的存储值权重矩阵,bc为当前时刻偏差向量。
(3)
(4)
通过输出门的控制函数ot对当天染疫数据预测值的输出控制,并通过转换得到预测值,计算公式如式(5)、式(8)所示:
(5)
(6)
(7)
(8)
在染疫人数预测输出中,Lt为实际值,通过输出门的控制函数ot对当天染疫人数预测值的输出控制,并通过转换得到染疫人数预测值,bo为当前时可偏差向量,Wy为输出门上一时刻染疫人数的存储值权重矩阵,Wo为控制门染疫人数真实值的权重矩阵,minJ(θ)为LSTM的损失函数。
本文构建的LSTM模型中三个门中的激活函数都采用的是Sigmoid函数,输出值在[0,1]之间,当输出值为0,此时对上一时刻的信息全部舍弃;当输出值为1,此时对上一时刻的信息全部保留。
1.2.2 模型搭建和预测
实验以新冠疫情为研究对象,获取2020年1月19日至2022年3月30日期间广东省每日新增确诊病例数作为实验数据。将2020年1月19日至2021年9月15日期间数据为训练集,搭建LSTM网络进行训练。2021年9月16日至2022年3月30日数据为测试集,对训练好的LSTM模型进行测试。
使用TensorFlow和Keras框架搭建LSTM网络模型,模型各配置参数如下:模型使用均方误差MSE作为损失函数,adam优化器。搭建的LSTM网络模型共有6层,包括3个LSTM层,2个dropout层和1个全连接层。第1个LSTM层连接输入,有100个神经元;第2、3层分别有100个神经元;为了防止过拟合现象,设置了两个dropout层,dropout率均为0.5;最后一层为输出层,只有1个神经元,使用全连接神经网络和线性激活函数linear输出预测值。
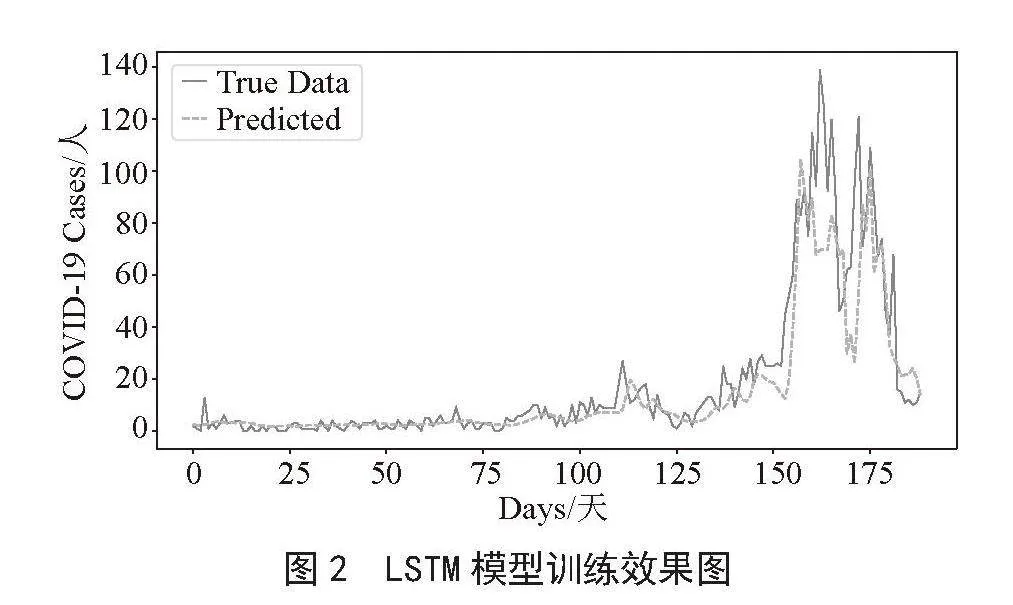
将广东省2020年1月19日至2021年9月15日期间每日新增确诊病例数为训练集,有590条数据。在训练时,时间窗口sequence_length长度为7,batch_size为32,epoch为1 500。模型测试集为广东省2021年9月16日至2022年3月30日期间的新增确诊病例数。训练结果如图2所示,其中横坐标表示预测时间,即从2021年9月16日起的预测天数,纵坐标表示新增确诊病例数,虚线表示预测结果,实线为实际数据。
训练结果的MAE与MSE值分别为6.08和139.63。以MAE和MSE两个数值作为评判指标来看,模型具有可观的预测效果;从预测值与真实值的对比图来看,预测结果与实际数据基本是吻合的,各新增高峰也进行了比较准确的预测,高峰数和出现高峰的时间与实际数据基本符合。综上说明模型获得了比较好的预测效果。
2 模型构建
2.1 场景分析
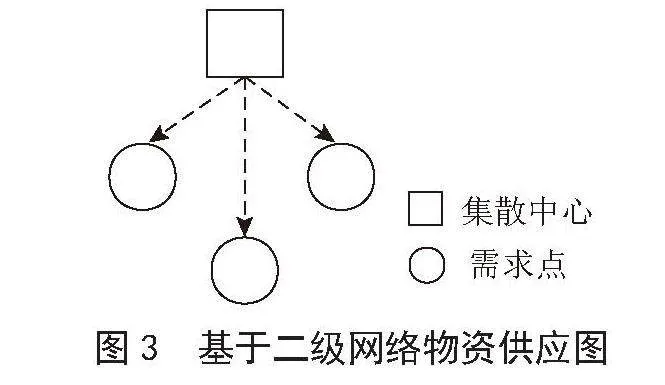
文章基于单周期二级节点网络进行研究,一个集散中心对应多个需求点,如图3所示。
每个集散中心的仓库大小、未来疫情发展等因素都存在差异。在这种情况下,需要确定每个需求点的需求,同时需要综合考虑多个因素,包括集散中心的仓库容量、物资的运输损耗以及多余物资存放产生的消耗。
2.2 物资需求模型构建
在对重大突发公共卫生事件下应急仓库订货数量建立模型之前,首先要在LSTM模型预测感染人数的基础上进行预测。按照前面对应急物资的分类,将物资分为医疗处置及救护物资和基本生活保障物资。在构建模型时,将医疗处置及救护物资分为整个病程所需要的药剂、救治类物品以及消杀类物资;将基本生活保障物资分为饮用水、食物以及其他必要生活物资。对于重大突发公共卫生事件t阶段每新增1个感染患者,对应需要的医疗处置及救护物资中整个病程所需要的药剂总量为αt,救治类物品总量βt,消杀类物资总量γt。设在重大突发公共卫生事件t阶段,每增加1个感染者对应有nt个人需要隔离,按照成人每人生活标准配置每人一套生活物资,包括饮用水w、食物f以及其他必要生活物资z。
综上所述,在重大突发公共卫生事件t阶段,每增加1个感染者所需要的物资需求量的计算公式为式(9)所示:
(9)
则在重大突发公共卫生事件t阶段每日需求量计算公式为式(10)所示,式中Ijt为重大突发公共卫生事件t阶段第j个需求点的感染人数。
(10)
2.3 仓库订货数量模型构建
综合考虑各方面因素,将以物资需求、储存成本、交通成本因素为基础,构建订货数量公式,如式(11)所示,式中Qt为重大突发公共卫生事件t阶段的物资需求量,SCk为第k种物资存储成本,TCk为第k种物资交通成本。
假设对每种物资从0开始进行编码,其中第k种物资存储成本计算式为式(12),式中Lk为第k种物资订货数量,Qi为第i天的物资消耗,θk为每单位第k种物资在仓库存放一天的物资损耗,d为存放天数,计算公式为式(13),为剩余可容纳仓储。第k种物资交通成本公式为式(14),式中λk为运输损耗率,μk为第k种物资运输数量。
(11)
(12)
(13)
(14)
3 算例分析
使用深圳市2022年10月1日至2022年10月14日物资需求情况作为算例,预测周期为7天,以10月1日至10月7日的新增病例数为基础,对10月8日至10月14日的物资需求进行预测。使用LSTM模型预测出10月8日至10月14日的每日新增病例数分别为81、73、47、23、23、23、14,共284人。
3.1 物资需求计算
根据《新型冠状病毒感染诊疗方案(试行第十版)》,基础治疗药品主要为退烧药和止咳祛痰药物,本文以布洛芬和连花清瘟胶囊为例进行需求量计算。危重症药物主要包括抗病毒药物、激素类药物等,本文以奈玛特韦片/利托那韦片、阿兹夫定片为例。按照新型冠状病毒救治经验,将上述药品设为治疗整个病程的一套用药,设病程为14天,药品病程计量如表1所示。
经计算可知,αt=46.67。对于确诊病例,每天需要进行3次核酸检测,病程内需要检测试剂42套,即βt=42。设每间病房平均面积为35平方米,每间病房住三名患者,则平均每名患者占用约12平方米,消杀类物资选取含氯消毒片,设每平方米消毒剂用量为0.1 L,参照中国医院协会发布的医院环境消毒及医疗废物等管理规范建议,每天消毒两次,则病程内需要消毒剂33.6 L,假设使用含氯消毒片配置消毒剂,每片加水1 L,则病程内每个患者需要33.6片含氯消毒片,则γt=33.6。
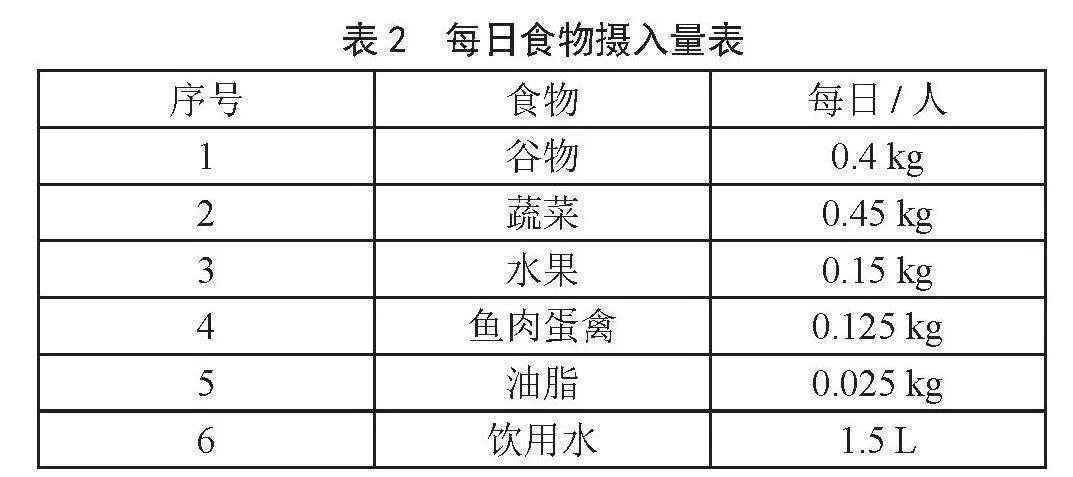
根据《中国居民膳食指南》,成年人每天应摄取至少包括谷物、蔬菜、水果、鱼肉蛋禽和油脂类食物。每种食物具体摄入量如表2所示。
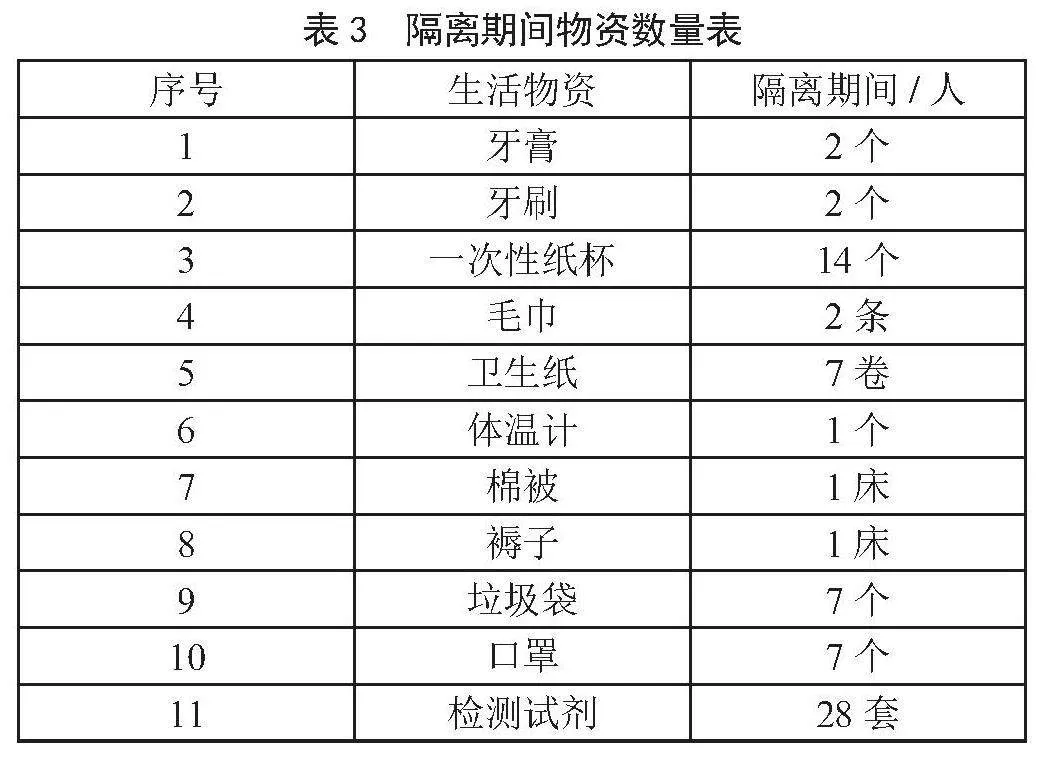
根据北京经济开发区网站发布的隔离物资准备,可知隔离点一般为隔离人员准备了牙膏、牙刷、一次性纸杯、毛巾、卫生纸、体温计、棉被、褥子、垃圾袋、口罩、检测试剂等生活必需物资,每种物资数量如表3所示。
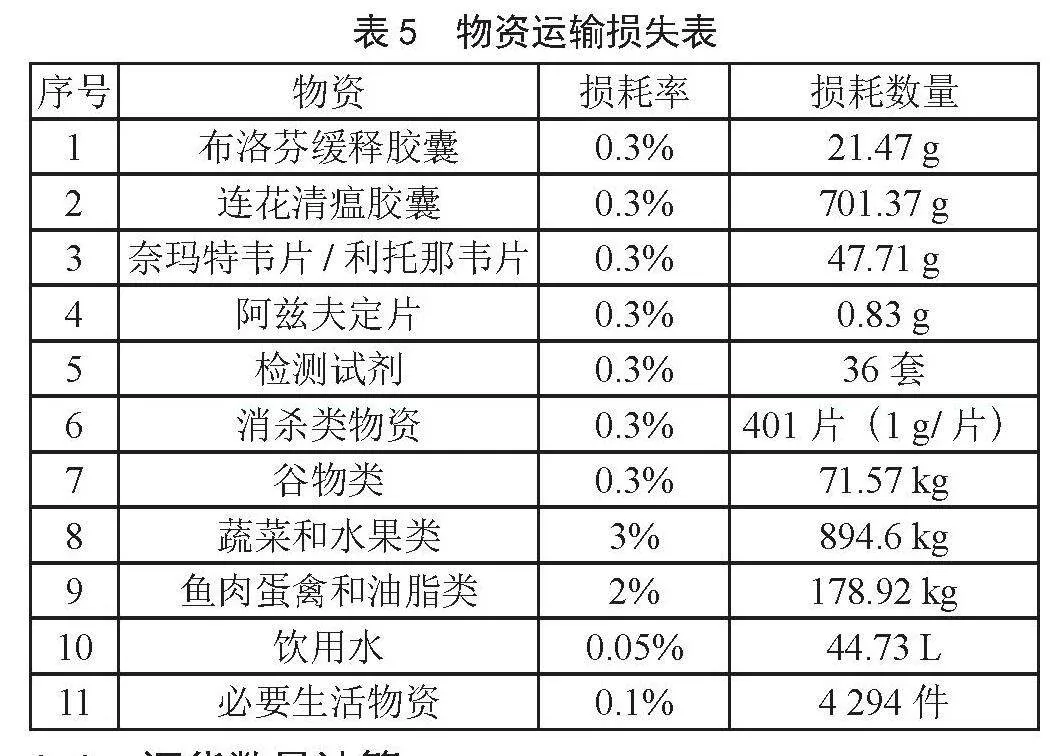
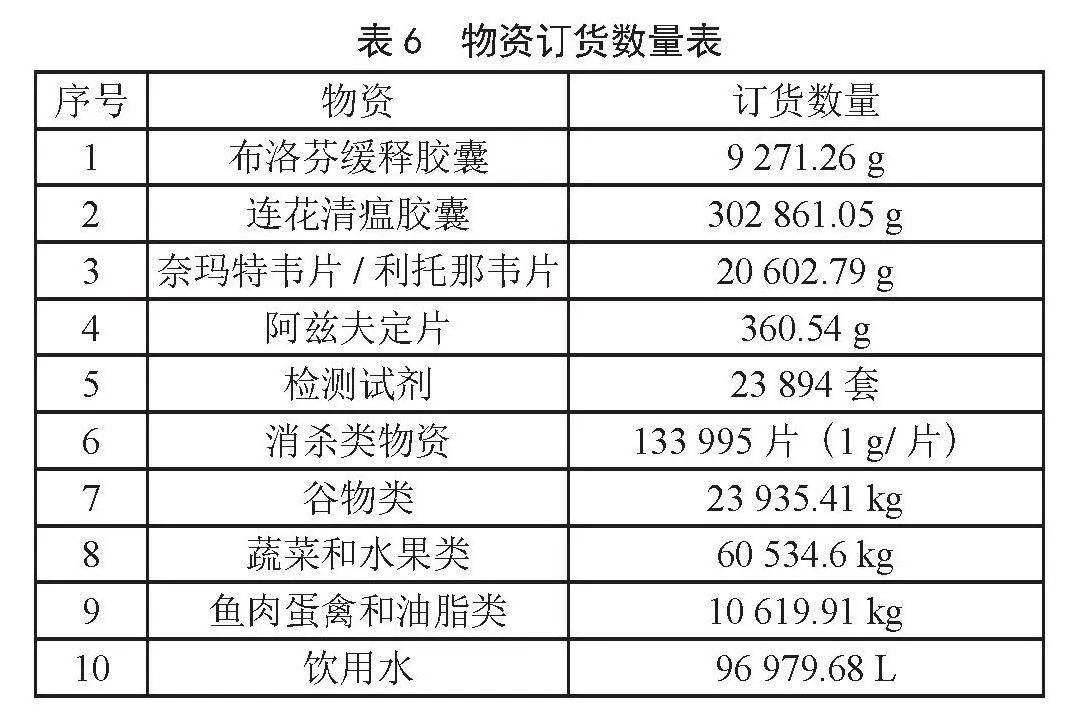
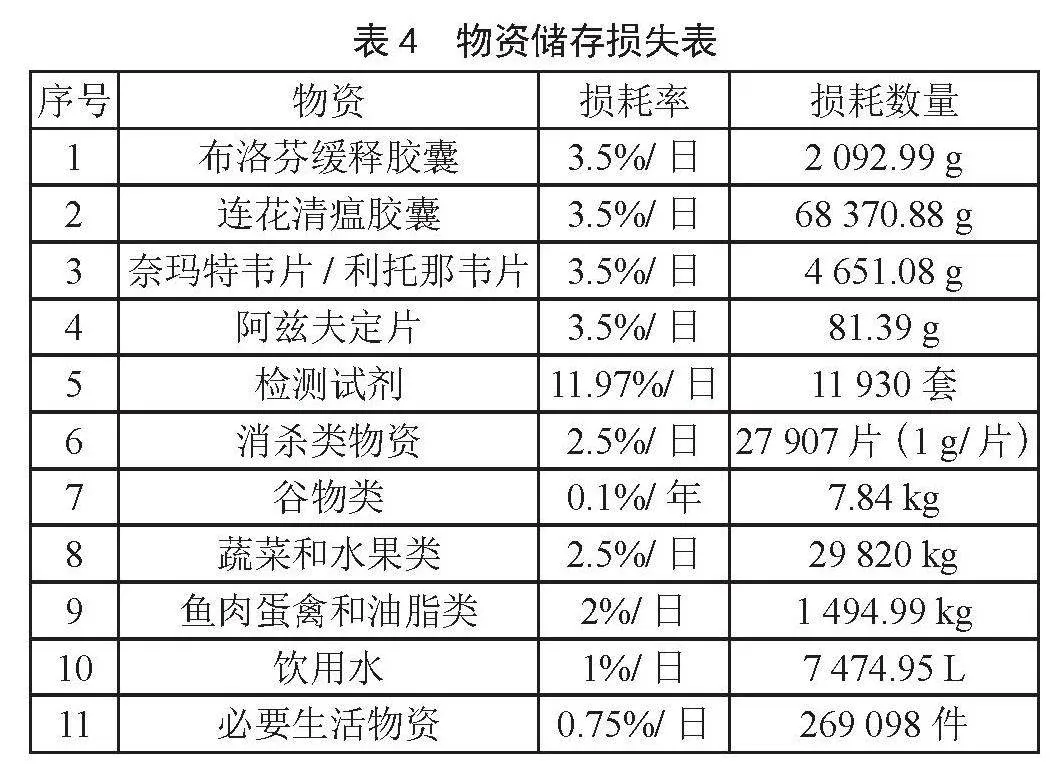
设平均每名感染者的密切接触者为15人[11]且全部被隔离,隔离时间为14天,则nt=15。按照式(13)和式(14)计算可得,需要药品:布洛芬缓释胶囊7 156.8 g,连花清瘟胶囊233 788.8 g,奈玛特韦片/利托那韦片15 904 g,阿兹夫定片278.32 g;需要检测试剂11 928套;需要含氯消毒片133 593.6片;需要饮用水89 460 L;需要谷物23 856 kg,蔬菜和水果29 820 kg,鱼肉蛋禽和油脂8 946 kg;需要必要生活物资4 294 080件。
3.2 成本计算
对于储存成本计算,假设仓库中已经储存了3.1中的物资需求量,根据《医药商品定额损耗管理办法》和《超市生鲜损耗率参考标准》等,每种物资损耗率和损耗量如表4所示。
交通成本是物资在运输过程中造成的损耗,假设每次运输的物资量为3.1中的需求量,根据商业部关于印发《商品运输定额损耗》的通知等,取平均损耗率,每种物资损耗率和损耗量如表5所示。
3.3 订货数量计算
根据3.1和3.2中的计算结果,代入到式(11)中计算可知各种物资订货数量,如表6所示。
4 结 论
本文首先研究重大突发公共卫生事件下应急物资分类,然后基于LSTM模型对感染人数进行预测,并在此基础上综合储存成本和交通成本构建订货数量模型,以深圳市为例,计算了十余种物资的订货数量。相较于传统的订货模型的研究,基于感染人数预测的订货模型研究可以掌握疫情发展趋势和明确物资需求量,有利于明确订货数值,从而为整个应急物资供应链提供可靠的数据。
参考文献:
[1] BALLER A C,DABIA S,DULLAERT W E H,et al. The Dynamic-Demand Joint Replenishment Problem with Approximated Transportation Costs [J].European Journal of Operational Research,2019,276(3):1013-1033.
[2] BRAGLIA M,CASTELLANO D,SONG D P. Distribution-Free Approach For Stochastic Joint-Replenishment Problem With Backorders-Lost Sales Mixtures, and Controllable Major Ordering Cost and Lead Times [J].Computers & operations research,2017,79:161-173.
[3] CHEN Y R,YANG L,JIANG Y S,et al. Joint Replenishment Decision Considering Shortages, Partial Demand Substitution, and Defective Items [J].Computers & Industrial Engineering,2019,127:420-435.
[4] WANG L,FU Q L,LEE C G,et al. Model and Algorithm of Fuzzy Joint Replenishment Problem Under Credibility Measure on Fuzzy Goal [J].Knowledge-Based Systems,2013,39:57-66.
[5] 谢青凌.四川省应急物资储备体系分析与优化 [D].成都:电子科技大学,2021.
[6] 李辉.应急物资分类标准与编码规范研究 [J].标准科学,2017(7):18-24.
[7] 康明.面向突发公共卫生事件的应急物资分类与调度问题研究 [D].北京:北京邮电大学,2023.
[8] SHAHID F,ZAMEER A,MUNEEB M. Predictions for COVID-19 with Deep Learning Models of LSTM, GRU and Bi-LSTM [J].Chaos, Solitons & Fractals,2020,140:110212.
[9] 孙东旭.突发疫情应急医疗物资需求预测与调度研究 [D].武汉:华中科技大学,2021.
[10] 熊红林,冀和,樊重俊,等.基于LSTM-SVR模型的航空旅客出行指数预测 [J].系统管理学报,2020,29(6):1169-1176.
[11] YANG Z F,ZENG Z Q,WANG K,et al. Modified SEIR and AI Prediction of the Epidemics Trend of COVID-19 in China Under Public Health Interventions [J].Journal of Thoracic Disease,2020,12(3):165.
作者简介:时晓旭(1999—),男,汉族,山东泰安人,硕士研究生在读,研究方向:计算机应用技术、应急数据处理、时间序列预测;郭慧(1981—),女,汉族,河北秦皇岛人,副教授,博士,研究方向:机器学习和模式识别;赖俊业(1999—),男,汉族,重庆江津人,硕士研究生在读,研究方向:计算机应用技术、强化学习、应急数据处理;王养廷(1966—),男,汉族,河北承德人,教授,硕士,研究方向:信息系统应用软件开发、数据采集、分析处理、控制系统软件开发。
DOI:10.19850/j.cnki.2096-4706.2024.17.026
收稿日期:2024-04-01
基金项目:科技创新2030-新一代人工智能重大项目(2021ZD0114203)
Research on the Order Quantity of Emergency Warehouse Based on the Prediction of the Number of Infected People
SHI Xiaoxu, GUO Hui, LAI Junye, WANG Yangting
(School of Computer Science, North China Institute of Science and Technology, Langfang 065201, China)
Abstract: This paper predicts the number of infected pRDG9nIS4zjzHvMpDkCTX0bn+R7moMR/JFGKVsoC+oY0=eople based on LSTM model, constructs material demand model, and derives the order quantity of emergency warehouse. Firstly, this paper starts with the classification of emergency materials, paving the way for building an order model. Secondly, for the characteristics of the problem of predicting the number of infected people, LSTM is selected as the prediction model, and the LSTM model network is established. Finally, this paper considers various influencing factors to establish a formula for calculating the order quantity. The paper provides a quantitative method for the order quantity of emergency warehouse in single cycles during major public health emergencies, providing scientific data support for the storage and ordering of emergency materials in the supply chain.
Keywords: emergency warehouse ordering; emergency materials; LSTM model; prediction of the number of infected people