



摘" 要:由于数据有复杂性、多样性和不确定性的特点,聚类通常存在不确定性,这种不确定性是指聚类结果的不一致性,从而影响分析的准确性,而通过三支决策方法构建不确定域,对不确定域进行延迟决策,能够带来一系列的优势。近些年来,这个研究热点涌现许多重要的工作。对聚类不确定的三支决策方法模型和研究方向进行介绍,按照三支聚类构建过程中遇到的问题进行总结。首先,给出三支聚类的表现形式。其次,分别阐述如何构建三支聚类的核心域和边界域,如何确定阈值,如何设计有效性指标,并介绍其中具有代表性的工作。最后,对聚类不确定的三支决策方法进行总结,并展望未来的研究方向。
关键词:聚类;不确定性;三支聚类;核心域;边界域;阈值;有效性指标
中图分类号:TP391" " " 文献标识码:A" " " 文章编号:2096-4706(2024)18-0025-09
Summary on Three-way Decision Method for Clustering Uncertainty
NIE Bin, JIN Haike, ZHANG Yuchao, ZHENG Xuepeng, CHEN Xingxin, MIAO Zhen, LI Huan
(College of Computer Science, Jiangxi University of Chinese Medicine, Nanchang" 330004, China)
Abstract: Due to the characteristic of complexity, diversity and uncertainty of data, clustering usually has uncertainty, which refers to the inconsistency of clustering results, thus affecting the accuracy of analysis. The Three-way Decision method can bring a series of advantages by constructing an uncertain domain and making delayed decision on the uncertain domain. In recent years, a lot of important work has emerged from this research hotspot. This paper introduces the model and the research direction of Three-way Decision method with clustering uncertainty, and summarizes the problems encountered in the construction process of Three-way Clustering. Firstly, the expression form of the Three-way Clustering is given. Secondly, the paper describes how to construct the core domain and boundary domain of the Three-way Clustering, how to determine the threshold value and how to design the validity index, respectively. It also introduces the representative work among them. Finally, the paper summarizes the Three-way Decision method of clustering uncertainty, and looks forward to the future research direction.
Keywords: clustering; uncertainty; Three-way Clustering; core domain; boundary domain; threshold value; validity index
0" 引" 言
聚类是一种典型的无监督数据分析方法,聚类分析是根据对象间的相似程度将对象集合进行分类,使得同类中的对象具有很高的相似性,而和其他类中的对象很不相似,旨在发现数据间有意义的合理划分,从而揭示数据内在的结构特征[1]。聚类在机器学习[2]、数据挖掘[3]、图像分割[4]、模式识别[5]、生物信息学[6]和自然语言处理[7]中都发挥着重要的作用。
随着数据爆炸式增长,人类面临的数据分类问题更加复杂。特别是数据的复杂性、多样性和不确定性问题的出现,导致分类结果的不一致性,从而影响分析的准确性。
数据的复杂性、多样性和不确定性主要体现在以下方面:1)因为样本类内差异大,而类间差异性小,类别多样,包含广泛。造成细粒度分类问题与粗粒度分类问题并存的状况[8],由于类别之间的相似程度大的情况存在,如何准确地对细粒度的类别进行更好的划分是目前面临的一大挑战。2)由于大量的样本靠近决策边界,甚至还有部分离群点的出现。这种样本主要包括处于不同类别重叠区域的数据以及存在较多孤立的噪声。其中,处于不同类别重叠区域的样本,它们与两个类中心之间的距离都很接近;而孤立的样本点与其他样本点之间的距离都较远,这种样本由于属性信息的不充分就难以准确地划分到确切的类别。3)建模类别数目多,导致建模难度高的问题。过去,多分类任务往往会转化为多个二分类任务,而当类别数量非常大的时候,特征空间中会出现大量的不可分的区域[9],对聚类结果会产生无法忽视的影响。4)由于训练集与测试集样本分布不一致影响模型表现。比如在薄膜包衣过程中有随机性和动态性的特点,每分钟近红外探头获得的光谱数据会存在比较大的差异[10],即用来训练目标检测模型的数据集与使用模型进行测试的数据集不一致,若使用新旧样本重新聚类,那么其预测性质已经变化,并不是原训练集模型,这也会导致聚类的不确定性。5)由于不确定数据的存在导致的聚类不确定性。从产生角度而言,不确定数据分为两种,包括客观存在和主动产生的。一些无法避免的因素,如由于设备测量误差、网络传输干扰等产生的不确定数据属于前者;而如在金融或者医疗领域里,会对用户敏感信息进行扰动等主动产生的不确定数据属于后者[11]。
面对以上情况带来的聚类不确定性,许多新的聚类策略应运而生,Höppner[12]提出了模糊聚类,定量地描述类的边界,用模糊集表示聚类结果,但不能很好地反映聚类结果的结构特征且很难刻画概念的模糊性边界。Pawlak[13]提出粗糙集理论,采用上近似和下近似来对目标集合进行逼近,从而得到一个近似描述,很好的描述了概念模糊边界问题。Lingras[14]提出了粗糙聚类,聚类结果由粗糙集的正域,边界域和负域来表示。基于概率粗糙集理论,Yao[15]提出了三支决策(Three-way Decision),结合“分而治之”“三分而至”的思想,用来处理不确定性问题[16],Yao[17]在考虑错误分类成本的条件下,证明了相比二支决策概率三支决策会更有优势,且Yao[18]给出了三级思维的基本问题和组成部分,以及一个感知-认知-行动三级概念模型。近年来,三支决策模型已成功应用在情感分析[19],医疗系统[20],属性约简[21]等领域。
Yu[22]受到三支决策思想的启发,提出了三支决策聚类方法,简称三支聚类(Three-way Clustering),将类用核心域、边界域和琐碎域来表示。利用三支决策处理聚类不确定性问题会有以下的优势:1)粗粒度空间下处理具有不确定性的信息时,只有在信息充分的情况下才会做出决策,而对于信息不充分的剩余对象将保留至更细粒度的空间,需要等到获得更多信息后再做出决策。2)将复杂多样的样本聚类问题进行分解能有效降低建模难度。3)由于现实中的决策往往是动态演变的过程,三支决策聚类能够较好改善传统二支决策的局限,这种方法能更好的符合当今社会的动态性和多元性。4)三支决策聚类能较好的处理对象与类簇之间缺乏明确归属关系的问题,能够更加精确的描述类簇的结构特征。
聚类不确定性中,根据三支决策聚类构建过程中遇到的一些问题,来设计高效的三支聚类算法,从而提高聚类质量,可以分为几点:1)三支决策聚类方法的构建,怎样合适的构建三支聚类,即应该如何构建核心域和边界域?2)三支决策聚类阈值的确定问题,如何进行优化确定阈值从而更好的估计不确定域,改进算法性能?3)三支决策聚类性能的评价,传统的评价指标是否适应于目前?如果不适用,那么如何设计新的有效性指标能够得到更好的聚类结果?
虽然Campagner[23]具体介绍了一个用三支决策处理机器学习中不确定性问题的模型,但是本文将基于以上3个基本问题进行详细分析,对现有方法进行讨论,综述现有的相关工作,分析此研究当前存在的问题,展望有待解决的问题。
1" 方法模型
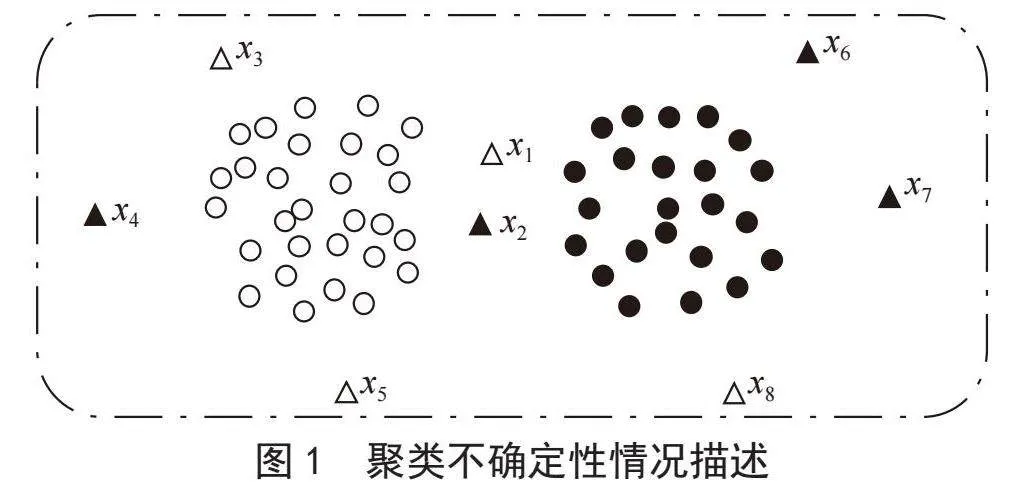
如图1所示,有两个高度集中的区域和分布在这两个区域附近的8个离散点,x1,x2,x3,…,x8。若采用传统的聚类方法,则需要将x1和x2,分配到左边或者右边的类簇中,但显然,x1和x2分到其中一个类簇而不是另外一个类簇中都是不合理的,因为它们与这两个类簇之间的距离几乎相同。而对于x3,x4,…,x8这几个离散点来说,虽然它们可以比较容易地分到某一个类蔟中,但是将它们包含在聚类中会削弱聚类的整体结构。
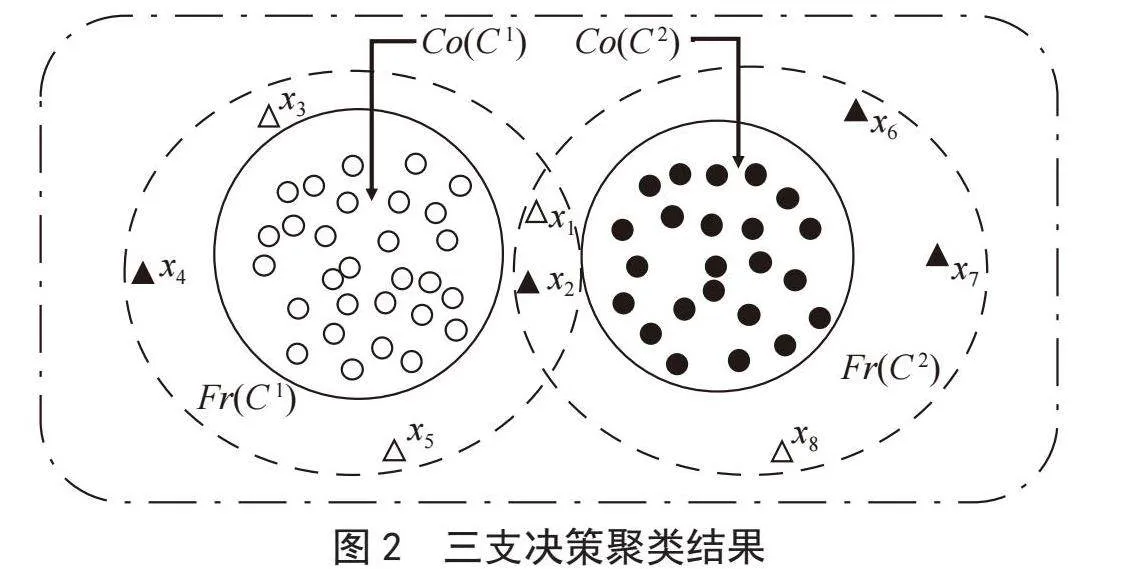
用三支决策的方法对样本进行聚类,如图2所示,将样本划分到C1和C2两个类簇,而对于不确定的样本,便将其划分到类簇C1和C2的边界域中。
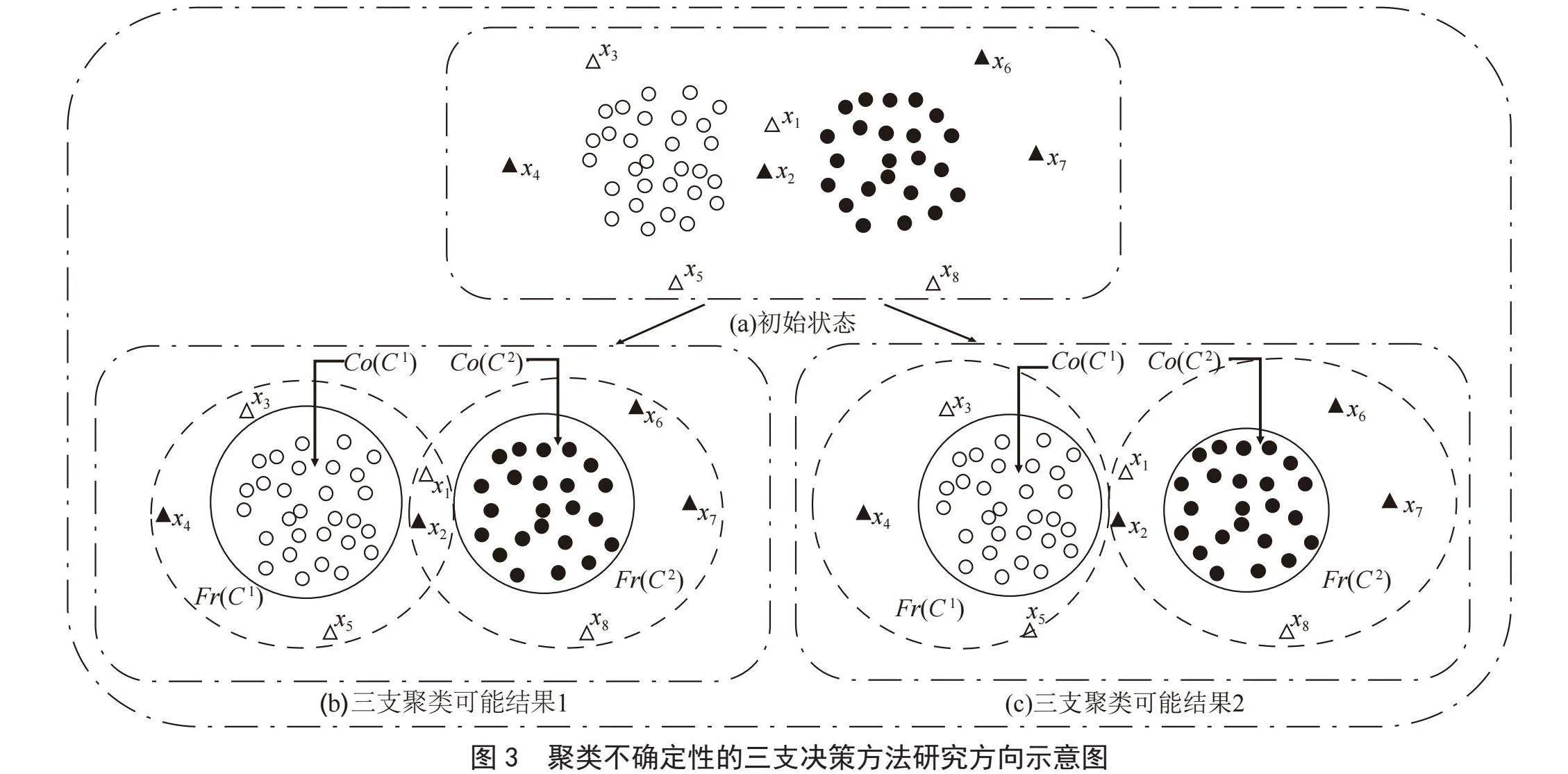
基于以上的基本问题,对现有文献进行归纳,图3描述了聚类不确定性的三支决策方法研究方向示意图,由(a)如何到(b)(c),即核心域和边界域是用怎样的方式构建,将在第3节进行介绍;若用一对阈值和评价函数得到(b)或者(c),即如何对阈值进行确定,从而更好地构建不确定域,将在第4节进行介绍;如何评价三支聚类结果,即对于(b)和(c)哪种结果能更好的体现聚类质量,将在第5节进行介绍。
2" 三支聚类表示
设讨论的对象集合为U={x1,x2,…,xi…,xN},传统的二支聚类的结果表示形式为CS={C1,C2,…,Ci,…Ck}。其中,x={x1,x2,…,xd,…,xD},k表示类的个数,D表示集合中的x具有的属性量,xd表示集合中的x在属性d上的取值,xd=n∈[1,N]。
在三支决策聚类中,对于任何数据U中的对象x,都一定属于一个类簇或多个类簇。对于任何一个类簇C中的数据对象,都将被表示为互不包含的三部分,即CL,CM,CR,又称为L域、M域和R域。在三支聚类结果中,R域中的对象对于类簇表示并没有实际意义,且有以下关系,CR=U-(CL∪CM),故类簇C可表示为C=(CL∪CM)。
基于一般的二支决策的类的表示形式,三支聚类可表示为:
C=(CL∪CM),C={Co(C),Fr(C)},其中,Co(C)⊆U,Fr(C)⊆U,设Tr(C)=U-Co(C)-Fr(C)。其中,Co(C),Fr(C),Tr(C)代表三支聚类所划分的三个域,即核心域、边界域和琐碎域。如果x∈Co(C),那么对象x确定属于类C;如果x∈Fr(C),那么对象x可能属于类C;如果x∈Tr(C),那么对象x确定不属于类C。则三支聚类结果表示为如下:
(1)
采用这种表示方式,可以更加直观体现出数据对象确定属于或可能属于某个类簇,通过对边界域中的数据进一步处理,能够更加清楚的了解到其对类簇的影响程度。
这些子集满足如下形式:
(2)
另一个方面,定义一个类,满足以下性质:
(3)
从信息融合的角度,考虑其交互程度,均体现了聚类的实际意义。从数据组合层次上来说,核心域不能为空,所有核心域、边界域和琐碎域的并集构成了整个对象集合;从数据整合层次上来说,每个类中至少有一个对象,且每个对象至少被划分到一个类中,每个类的核心域、边界域和琐碎域,其中两两相交都为空集;从数据聚合层次上来讲,每个类的琐碎域可由集合U对核心域和边缘域作差集得到。
3" 核心域和边界域的构建
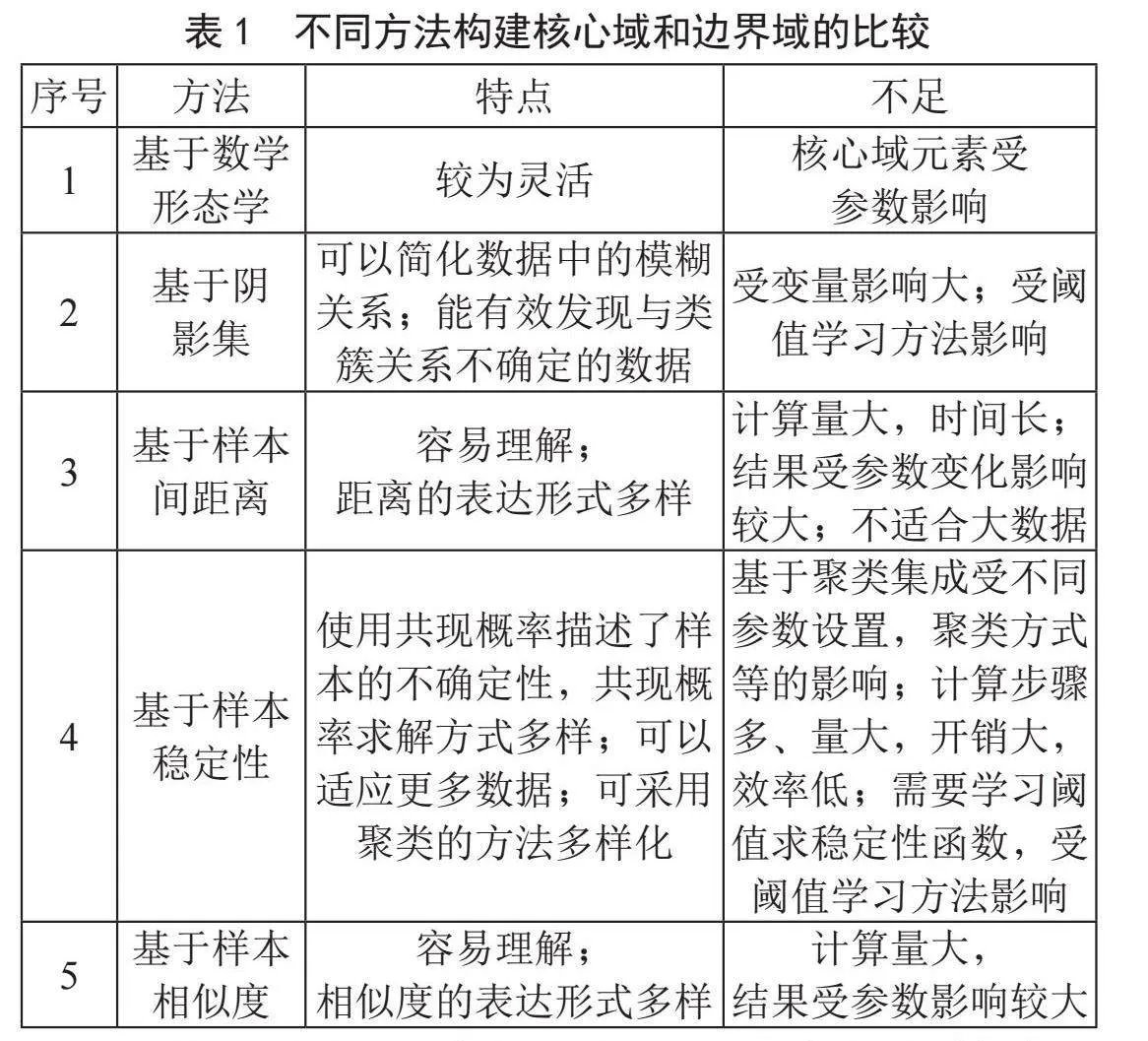
在聚类不确定性的三支决策方法中,对于如何获得核心域和边界域的相关内容是研究的关键问题,根据其采用的主要方法,大致可以分为5类。表1归纳了采用不同方法构建核心域和边界域的特点和不足。
3.1" 基于数学形态学
数学形态学最初是Matheron和Serra[24]为实现任意集合的大小改变而实现并为其奠定了理论基础,Wang[25]等将数学形态学理论中的侵蚀和膨胀思想引入聚类中,提出了一种基于数学形态学的三支聚类算法,即CE3(Contraction-and-Expansion Based Three-way Clustering)框架,其使用收缩操作得到三支聚类的核心域,使用拓展操作将聚类放大作为支撑,支撑和核心点之间的差异为边缘区域,代表一个蔟的不清晰边界。刘强[26]利用二值图像腐蚀和膨胀的思想,给出了一种将二支聚类的结果转化为三支聚类结果的方法,将对象的 邻域定义为结构算子,利用结构算子对二支聚类的结果进行收缩和扩张得到三支聚类的核心域和边界域,确定的元素划分至核心域,不确定的元素划分至边界域中进行延迟决策,聚类总体性能和平均性能都有所提升,但是该方法是在传统二支聚类基础上再进行三支聚类的,不具有动态性。
3.2" 基于阴影集
阴影集由Pedrycz[27]于1998年首次提出,是一种基于区间代数的模糊集合表示方法,通过精确的隶属度值识别类簇边界模糊的现象,可以更准确地表示模糊度,更好地处理模糊集合的差异性,并且可以处理不确定性,加强结果的可解释性。姜春茂[28]提出了一种基于阴影集的多粒度三支聚类集成算法,首先以模糊聚类(Fuzzy C-means, FCM)为基聚类,得到了一组具有差异性的基聚类成员,对象与类簇的关系以隶属度矩阵来表示,根据阴影集的三种操作构造三支聚类,将对象划分至核心域和边界域,但是该算法的结果可能会受到基聚类中个别低质量聚类成员的影响。Jiang[29]提出通过可能性C-均值聚类(Possibilistic C-Means clustering, PCM)生成一组基类成员,将所有对象根据其可能隶属度初始划分为三个域,即核心域,边缘域和琐碎域,引入多粒度粗糙集,分析对象和类簇之间的不确定性,将对象划分为4个近似区域,再利用阴影集检查以上4个区域,最终输出三支聚类结果,但是该算法的聚类结果对聚类成员尺度不敏感。William[30]提出了一种基于阴影集的三支聚类方法,利用阴影集框架,定义一系列新的基于优化的原则,包括确定域和不确定域的权衡原则、锐度平衡原则和渐进式平衡原则,并确定最佳阈值,得到三个近似区域,但是该算法没有考虑样本量对数据结构分类性能和学习的影响。
3.3" 基于样本间距离
对象x的q近邻是指距离x最近的q个对象集合,于洪[31]在基于邻域的基础上,从类内紧凑性和考虑近邻类间分离性角度出发,提出了一种自动三支决策聚类算法,根据类中对象的邻居和其他类之间的关系,以及类中对象之间的差异性,将对象分到核心域和边界域。王平心[32]提出了一种基于动态邻域的三支聚类分析方法,该方法分别采用K-means算法和谱聚类算法得到二支聚类,再利用二支聚类的结果和每个类中元素的邻域是否完全包含在该类中来对集合进行收缩,同时利用不在该类中的元素的邻域是否与该类有交集进行扩张,其中收缩的区域称为核心域,扩张域和核心域的差集称为边界域,该方法很好地提升了聚类结果的结构。于洪[33]提出了差值排序法,计算类中对象到类中距离的差值对类中对象做进一步区分,计算对象到类中心的距离,按照从小到大的顺序排列,用距离差值将对象分别划分至核心域和边界域。Fan[34]提出了一种新的基于三支密度敏感谱聚类算法,该算法提出密度敏感距离,代替欧氏距离,创建相似矩阵,将密度敏感距离度量与三支聚类结合,在密度敏感谱聚类过程中采用重叠聚类方法,引入容差参数,将核心域和边缘域的并集表示为一个蔟的上界,再进行扰动分析,将每个簇的核心域从上界中分离出来,但是该方法受参数的动态影响较大,且其中过程计算时间长,不适合大数据。
3.4" 基于样本稳定性
Li[35]在聚类集成背景下从多个划分的角度估计了两样本的共现概率,研究了样本关系的不确定性,提出了样本稳定性的概念来发现具有稳定关系的样本集,基于一组聚类结果,计算共现概率,即任意两个样本被划分在同一类的频率,当两样本的共现概率为1时,表明这两个样本始终在同一类,若为0时,表明始终不在同一类,以上两种情况都说明两样本之间具有较高的稳定关系,若介于0和1之间说明它们的关系具有一定的不确定性。花遇春[36]在样本稳定性的共现概率的基础下,给出了基于 个类簇的共现概率的三支聚类方法,根据两个样本隶属于同一类簇的共现概率刻画样本之间的关系,从而获得三支聚类的核心域和边界域。Wang[37]提出了一种基于样本稳定性的三支聚类算法,该算法以一组基聚类作为输入,利用协同矩阵和一个确定性函数来计算样本稳定性,并以样本稳定性阈值将论域分为核心域和边界域,将样本稳定性高的构成核,再利用K-means算法划分核心域,边缘域由稳定性较低的样本构成,该算法很好的揭示了聚类结构。
3.5" 基于样本相似度
样本相似度是指两个或多个样本在某些方面的相似性或接近程度。Yu[38]改进了相似度的计算,采用改进的基于密度的噪声应用空间聚类(Density-Based Spatial Clustering of Applications with Noise, DBSCAN)算法获得聚类初始结果,首先,对于每一个簇,将目标密度与阈值进行比较,构造核心域和边界域,其次,扩大类簇的边界域,最后,再获取更多信息后,将噪声点分配到类簇的边界域,得到了更好的聚类结果,有效的处理了元素和类之间的关系,但是该方法是将硬聚类算法结果提取为三支聚类,在一定程度上依赖于硬聚类算法的性能。Yu[39]改进现有的欧氏距离,提出了一种新的不完全数据之间的相似性度量,并将改进后的欧氏距离作为评价函数,且应用于三支聚类模型中。
另外更多的是结合三支聚类开发新的算法,Shi[40]首先使用谱聚类算法获取每一类簇的上界,然后根据对象和类簇的关系,更新类的上界和聚类中心,再计算新旧聚类中心的距离,将每一类蔟的上界进一步细分为核心域和边界域,用三只谱聚类方法将数据集中的样本划分为类内相似度高,类间相异度高的聚类结果,有较好的聚类效果,但是该算法有待进一步修改和完善。Du[41]在序贯三支决策的基础上提出了一种多步三支聚类,首先使用渐进侵蚀策略构建数据多层结构,以便高层次能够从低层次收集更多信息,高层数据来自核心域,可以更好地分离和聚类,而低层次数据更多可能来自边界域,然后在考虑每个侵蚀实例的邻域信息后,采用自适应方案确定每个实例的阈值,在自适应方案下,采用基于连通性的方法对高层次数据聚类,采用基于延迟决策的“两阶段”方法分配低层次数据,该方法按照从高到低的层次逐步确定了每个类簇的核心域和边界域。
4" 阈值的确定方法
在聚类不确定性的三支决策学习方法中,Yu[42]使用评估函数和评估函数的一对决策阈值(α,β)且α≥β,通过阈值和评价函数的值来构建三支聚类的三个区域,评估函数量化了一个对象和一个集群的关系,而阈值定义了不同区域的边界。基于评价函数v(x),可以得到以下的三支决策规则:
(4)
在实际的应用场景中,评价函数可以是代价函数、相似度函数等,基于全序的评价函数虽然在计算上存在优势,但仍存在一定的局限性;现有的三支聚类往往根据主观调优选择合适的阈值,或采用固定的阈值,但主观划分阈值的方法不能针对不同大小和密度的数据集而自动划分阈值,因此不能准确的揭示数据集的聚类结构。阈值的确定问题是一个优化问题,能够提高聚类的整体质量,最大化每个聚类所含样本的准确性,最小化最终聚类结果的表示的不确定性,对于准确而有效的估计不确定区域至关重要,而现有研究对阈值确定的问题研究还不够充分,对于最佳阈值的确定已经成为一大挑战。根据其采取的策略,大致可以分为2类,表2归纳了采用不同策略确定阈值的特点和不足。
4.1" 基于平衡策略
Afridi[43]利用博弈论粗糙集的原理,在精确性和类簇通用性之间取得平衡,修改阈值可以提高通用性,聚类点数量会影响通用性,通过确定阈值以实现准确性和通用性之间的平衡,再利用确定的阈值对不确定性数据进行聚类分析,对完整信息数据做划分处理,对不完整数据做延迟处理,该方法很好地提高了聚类精度,但是该方法受迭代停止条件的影响。Afridi[44]提出了一种基于方差的三支聚类方法,利用优化标准自动确认阈值,考虑评价函数值的两类方差,即区域内方差和区域间方差,前者是度量对象评价函数值在一定区域内的分布情况,后者是衡量评估函数在基于区域的平均值与评估函数值的全局平均值之间的分布,结合遗传算法并考虑两类方差的优化标准来确定阈值,该方法能很好的估计重叠区域。
4.2" 基于最小最大化策略
Jia[45]提出了一种阈值自动选择算法,基于样本相似度来定义粗糙度以此测量边缘区域的不确定度,并定义新的聚类有效性指数和分区有效性指数来度量聚类分区,首先计算所有可能对的样本相似度,选择候选阈值空间,计算有效性指数,使得最大有效性指数的阈值作为最佳阈值。李刘万[46]提出了一种阈值的自适应选择方法,首先计算样本相似度,设置恰当的步长遍历所有候选阈值,获得样本相似度最小值和最大值构成的候选阈值空间,对于每个候选阈值,计算目标子集所对应的核心域和边界域,得到当前划分的有效性指标,最后输出当前最大有效性指标值的阈值作为最优阈值。
另外,更多的是结合新的指标获取最佳阈值。Yu[47]提出了一种基于万有引力的三支聚类算法,由万有引力定律可知,核心域和边缘域之间的引力大于边缘域和琐碎域之间的引力,则使用万有引力公式作为评估函数自动获取阈值,将对象分配到相应领域的核心域、边界域和琐碎域,该方法在聚类过程中可以自动调整阈值,获得更详细的对象和聚类间的归属关系。Xiong[48]提出一种基于万有引力思想针对混合型数据的自适应三支聚类算法,在聚类过程中动态调整阈值,自适应的选择两个相邻局部质量轮廓物体之间引力最大值和最小值作为阈值,从而获得更好的聚类性能。
5" 有效性指标的设计
聚类有效指标对于产生最佳聚类结果十分重要,常用的聚类有效指标主要为内部指标和外部指标,内部指标通过考察聚类结果的紧致度、分散度、重叠度等特征来对聚类结果进行评估,常见的有DBI指数(Davies Bouldin Index)、DI指数(Dunn Index)和轮廓系数(Silhouette Coefficient),而外部指标通过将聚类结果与参考模型的输出相比较来评价聚类结果质量,常见的有纯度(Purity)、兰德系数(Rand Index, RI)、F值(F-measure)、归一化互信息(Normalized Mutual Information, NMI)和调整兰德系数(Adjusted Rand Index, ARI)。传统的聚类有效指标大部分是基于二支划分的,更多的关注聚类实例模型上的准确性,具有倾向性。
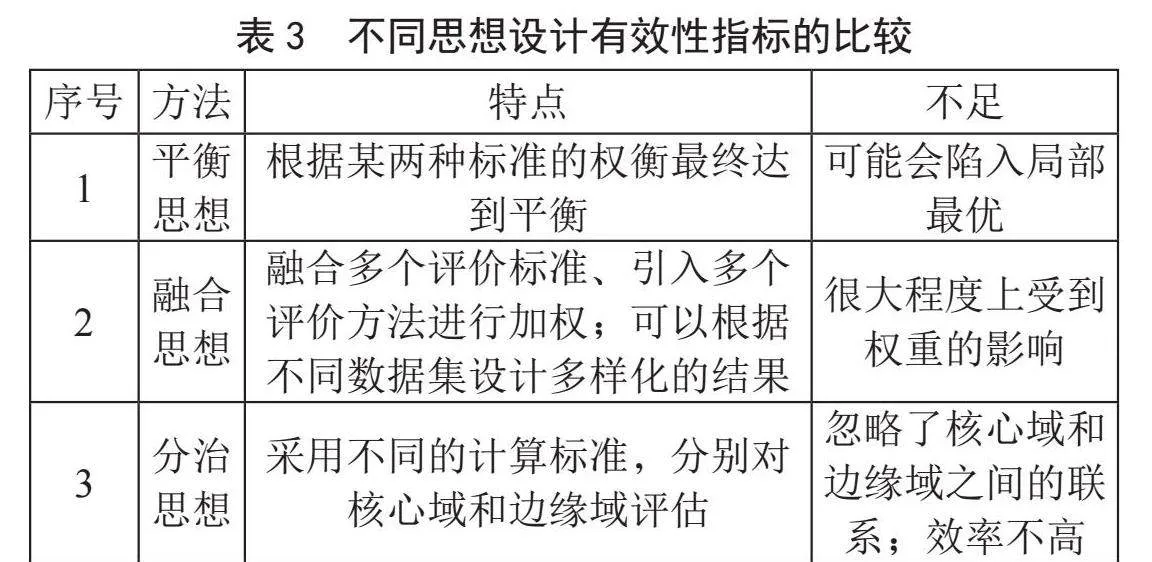
在基于三支决策的聚类不确定性问题中,很难体现数据在划分过程中的不确定性[49],评估他们的指标应该考虑实例聚类的准确性和算法的覆盖率之间的权衡,也就是边界域中的实例。根据其采用的主要思想,大致可以分为3类。表3归纳了采用不同思想设计有效性指标的特点和不足:
1)基于平衡思想。Beni[50]针对模糊聚类提出一种常用的模糊聚类有效指标XB,引入模糊因子,找到紧致度和分散度之间的平衡点,而确认最佳聚类数。
2)基于分治思想。夏月月[51]基于三支决策理论,提出了一种能有效评估样本空间且确认最佳聚类数的一种有效指标TVCI,该指标分别对核心域和边缘域评估,采用不同的计算规则。该指标对于评估聚簇质量有一定的效果,但存在数据量大时效率不高的问题。
3)基于融合思想。Sun[52]基于集成思想,引入多个有效性指标,首先通过三支聚类生成不同k值的聚类结果,并根据各评价结果与其他聚类结果的平均相似度对各评价结果进行加权,再综合多个有效性指标评价结果,选取排名最佳的k值作为可选聚类数。最终选择最有类簇数目。Jia[53]定义了一个新的聚类有效性指标,首先引入样本相似度定义粗糙度,其次定义新的分区有效性指标来度量聚类分区,然后引入类内类间相似性来描述样本与聚类簇之间的定量变化,在此基础上定义了一种新的聚类有效性指标来衡量不同聚类数量下的聚类性能。
另外,更多的是提出一种新的有效性指标。Peters[54]提出了一种改进的Davis-Bouldin指数来评估三支聚类,Depaolini[55]等提出了Rand、Jaccard和fowlkes-malos指数的推广,Campagner[56]提出了聚类质量的信息论度量和分类精度度量。
6" 结" 论
聚类不确定性的三支决策学习方法通过构建不确定域,能够高效地处理复杂的聚类。本文从构建过程出发,具体阐述了构建过程中的3个基本问题:如何构建核心域和边界域,如何确定阈值,如何设计有效性指标。并讨论了其中具有代表性的相关工作。尽管在聚类不确定性问题中,三支聚类方法的处理模式已经比较成熟,但仍然存在一些问题需要深入研究:
1)从理论研究上来看,需要进一步完善三支聚类理论的数学模型和算法,现有的三支聚类很多都是在传统的二支聚类完成后再进行三支聚类的,这在很大程度上忽略了每个对象的分布关系,如何将三支聚类动态的集成在二支聚类的中间过程中,或者直接从无到有构建三支聚类是下一步研究的方向;现有的三支聚类方法仍然存在一定的局限性,对于处理大规模和高维度数据,而且对于不同的应用场景,需要设计不同的算法模型。因此,需要在理论上进行深入研究和探索,以推动三支聚类理论的发展和应用。
2)从技术难点上来看,三支聚类将数据分为三个域,但是对于某些数据集可能不够灵活,无法满足更细粒度的聚类需求。当可以获得更多信息时,三支聚类边缘域中的不确定对象需要做进一步处理,如何满足更细粒度的聚类要求和如何对不确定中的对象做进一步处理将成为一大热点;聚类数量的选择和阈值的设定对三支决策聚类算法的效率会产生很大的影响,如何确定合适的聚类数目和阈值,使同一类簇内样本距离更近,不同类簇样本距离更远,是一个研究重点。
3)从应用交叉上来看,三支聚类可以与其他领域的研究进行交叉,以发现更多的应用场景和方法改进。例如,可以将三支聚类与机器学习、风险管理、人文社会科学、气象预测和智能交通等领域的研究进行交叉,以实现更好的聚类效果和决策精度。与机器学习领域的应用交叉表现为与深度学习相结合,以更好地处理大规模数据集的不确定性。与风险管理领域的应用交叉表现在金融、保险和医疗等行业的风险评估和决策中,可以用来对风险因素进行分类和评估,并根据评估结果制定相应的决策。与人文社会科学领域的应用交叉表现在人类行为的复杂性和主观性导致数据的不确定性,例如心理学和社会学等领域。与气象领域的应用交叉表现在大气运动的每一个环节都存在某些不确定性,比如应用于天气预报中的不确定性处理,以提高决策的准确性。与智能交通领域的应用交叉可以表现在交通流量预测、路况监测和智能交通控制中。可以用来对交通数据进行聚类和分类,并根据聚类结果制定相应的交通控制策略。
参考文献:
[1] AGGARWAL C C. Data Clustering:Algorithms and Applications [M].New York:Chapman and Hall,2014:2-3.
[2] AHUJA R,AAKARSHA C,SHAURYA G,et al. Classification and Clustering Algorithms of Machine Learning with Their Applications [J].Nature-inspired computation in data mining and machine learning,2020,855:225-248.
[3] BERKHIN P A. Survey of Clustering Data Mining Techniques [J].Grouping Multidimensional Data:Recent Advances in Clustering,2006:25-71.
[4] 石雪松,李宪华,孙青,等.基于人工蜂群与模糊C均值的自适应小波变换的噪声图像分割 [J].计算机应用,2021,41(8):2312-2317.
[5] 张德丰.聚类与动态RBF网络的模式识别应用研究 [J].计算机工程与应用,2009,45(16):204-207.
[6] KARIM M R,BEYAN O,ZAPPA A,et al. Deep Learning-Based Clustering Approaches for Bioinformatics [J].Briefings in Bioinformatics,2021,22(1):393-415.
[7] 贺佳,杜建强,聂斌,等.基于多节点组合特征和模糊聚类的中文词义消歧方法 [J].计算机应用与软件,2021,38(2):152-157+220.
[8] HE X T,PENG YU X,XIE L. A New Benchmark and Approach for Fine-Grained Cross-Media Retrieval [C]//Proceedings of the 27th ACM international conference on multimedia. New York:ACM,2019:1740-1748.
[9] 胡清华,王煜,周玉灿,等.大规模分类任务的分层学习方法综述[J].中国科学:信息科学,2018,48(5):487-500.
[10] 聂斌,陈裕凤,何雁,等.基于代表率与投票机制的分类方法监测片剂包衣终点的研究[J].山东大学学报:理学版,2022,57(11):78-88.
[11] 刘晗.不确定数据聚类分类研究[D]. 大连:大连理工大学,2018.
[12] HÖPPNER F,KLAWONN F,KRUSE R,et al. Fuzzy Cluster Analysis:Methods for Classification,Data Analysis and Image Recognition [M].Chichester:Wiley Press,1999:1-48.
[13] PAWLAK Z. Rough Sets [J].International Journal of Computer amp; Information Sciences,1982,11:341-356.
[14] LINGRAS P. Rough K-Medoids Clustering Using Gas [C]//2009 8th IEEE International Conference on Cognitive Informatics.Hong Kong:IEEE,2009:315-319.
[15] YAO Y Y. Three-Way Decisions with Probabilistic Rough Sets [J].Information Sciences,2010,180(3):341-353.
[16] 张清华,支学超,王国胤,等.基于属性代表的多粒度集成分类算法 [J].计算机学报,2022,45(8):1712-1729.
[17] YAO Y Y. The Superiority of Three-Way Decisions in Probabilistic Rough Set Models [J].Information Sciences,2011,181(6):1080-1096.
[18] YAO Y Y. Tri-Level Thinking: Models of Three-Way Decision [J].International Journal of Machine Learning and Cybernetics,2020,11(5):947-959.
[19] 王磊,黄河笑,吴兵,等.基于主题与三支决策的文本情感分析 [J].计算机科学,2015,42(6):93-96.
[20] 张萌,孙秉珍,楚晓丽.基于邻域代价敏感三支决策的痛风诊断模型 [J].计算机工程与应用,2020,56(16):218-225.
[21] 胡声丹,苗夺谦,姚一豫.基于三支标签传播的半监督属性约简 [J].计算机学报,2021,44(11):2332-2343.
[22] YU H,ZHANG C,WANG G Y. A Tree-Based Incremental Overlapping Clustering Method Using the Three-Way Decision Theory [J].Knowledge-Based Systems,2016,91:189-203.
[23] CAMPAGNER A,CABITZA F,CIUCCI D. Three-Way Decision for Handling Uncertainty in Machine Learning:A Narrative Review [C]//Rough Sets:International Joint Conference, IJCRS 2020.Havana:Springer International Publishing,2020:137-152.
[24] SERRA J. Introduction to Mathematical Morphology [J].Computer Vision,Graphics,and Image Processing,1986,35(3):283-305.
[25] WANG P X,YAO Y Y. CE3: A Three-Way Clustering Method Based on Mathematical Morphology [J].Knowledge-based systems,2018,155:54-65.
[26] 刘强,施虹,王平心,等.基于ε邻域的三支决策聚类分析 [J].计算机工程与应用,2019,55(6):140-144.
[27] PEDRYCZ W. Shadowed Sets: Representing and Processing Fuzzy Sets [J].IEEE Transactions on Systems,Man,and Cybernetics, Part B (Cybernetics),1998,28(1):103-109.
[28] 姜春茂,赵书宝.基于阴影集的多粒度三支聚类集成 [J].电子学报,2021,49(8):1524-1532.
[29] JIANG C M,LI Z C,YAO J T. A Shadowed Set-Based Three-Way Clustering Ensemble Approach [J].International Journal of Machine Learning and Cybernetics,2022,13(9):2545-2558.
[30] WILLIAM-WEST T,KANA A F D,IBRAHIM M A. Shadowed-Set-Based Three-Way Clustering Methods: An Investigation of New Optimization-Based Principles [J].Information Sciences,2022,591:1-24.
[31] 于洪,毛传凯.基于k-means的自动三支决策聚类方法 [J].计算机应用,2016,36(8):2061-2065+2091.
[32] 王平心,刘强,杨习贝,等.基于动态邻域的三支聚类分析 [J].计算机科学,2018,45(1):62-66+89.
[33] 于洪.三支聚类分析 [J].数码设计,2016,5(1):31-35+30.
[34] FAN J C,WANG P X,JIANG C M,et al. Ensemble Learning Using Three-Way Density-Sensitive Spectral Clustering [J].International Journal of Approximate Reasoning,2022,149:70-84.
[35] LI F J,QIAN Y H,WANG J T,et al. Clustering Ensemble Based on Samples Stability [J].Artificial Intelligence,2019,273:37-55.
[36] 花遇春,赵燕,马建敏.基于共现概率的三支聚类模型 [J].西北大学学报:自然科学版,2022,52(5):797-804.
[37] WANG P X,YANG X B. Three-Way Clustering Method Based on Stability Theory [J].IEEE Access,2021,9:33944-33953.
[38] YU H,CHEN L Y,YAO J T,et al. A Three-Way Clustering Method Based on An Improved DBSCAN Algorithm [J].Physica A: Statistical Mechanics and its Applications,2019,535:122289.
[39] YU H. A Framework of Three-Way Cluster Analysis [C]//Rough Sets: International Joint Conference.Olsztyn:Springer International Publishing,2017:300-312.
[40] SHI H,LIU Q,WANG P X. Three-Way Spectral Clustering [C]//Foundations of Intelligent Systems: 24th International Symposium.Limassol:Springer International Publishing,2018:389-398.
[41] DU M J,ZHAO J Q,SUN J R,et al. M3W: Multistep Three-Way Clustering [J].IEEE Transactions on Neural Networks and Learning Systems,2024,35(4):5627-5640.
[42] YU H,ZHANG C,WANG G Y. A Tree-Based Incremental Overlapping Clustering Method Using The Three-Way Decision Theory [J].Knowledge-Based Systems,2016,91:189-203.
[43] AFRIDI M K,AZAM N,YAO J T,et al. A Three-Way Clustering Approach for Handling Missing Data Using Gtrs [J].International Journal of Approximate Reasoning,2018,98:11-24.
[44] AFRIDI M K,AZAM N,YAO J T. Variance Based Three-Way Clustering Approaches for Handling Overlapping Clustering [J].International Journal of Approximate Reasoning,2020,118:47-63.
[45] JIA X Y,RAO Y,LI W W,et al. An Automatic Three-Way Clustering Method Based on Sample Similarity [J].International Journal of Machine Learning and Cybernetics,2021,12:1545-1556.
[46] 李刘万,朱金,王平心.基于样本相似度的三支聚类算法 [J].扬州大学学报:自然科学版,2022,25(6):40-44.
[47] YU H,CHANG Z H,WANG G Y,et al. An Efficient Three-Way Clustering Algorithm Based on Gravitational Search [J].International Journal of Machine Learning and Cybernetics,2020,11:1003-1016.
[48] XIONG J,YU H. An Adaptive Three-Way Clustering Algorithm for Mixed-Type Data [C]//Foundations of Intelligent Systems: 24th International Symposium.Limassol:Springer International Publishing,2018:379-388.
[49] YU H. A Framework of Three-Way Cluster Analysis [C]//Rough Sets: International Joint Conference.Olsztyn:Springer International Publishing,2017:300-312.
[50] XIE X L,BENI G. A Validity Measure for Fuzzy Clustering [J].IEEE Transactions on Pattern Analysis amp; Machine Intelligence,1991,13(8):841-847.
[51] 夏月月. 基于三支决策改进的K-means算法及聚类有效性指标研究 [D].合肥:安徽大学,2021.
[52] SUN N,YU H. A Method to Determine the Number of Clusters Based on Multi-Validity Index [C]//Rough Sets: International Joint Conference.Quy Nhon:Springer International Publishing,2018:427-439.
[53] JIA X Y ,RAO Y,LI W W,et al. An Automatic Three-Way Clustering Method Based on Sample Similarity [J].International Journal of Machine Learning and Cybernetics,2021,12:1545-1556.
[54] PETERS G. Rough Clustering Utilizing the Principle of Indifference [J].Information Sciences,2014,277:358-374.
[55] DEPAOLINI M R,CIUCCI D,CALEGARI S,et al. External Indices for Rough Clustering [C]//Rough Sets: International Joint Conference.Quy Nhon:Springer International Publishing,2018:378-391.
[56] CAMPAGNER A,CIUCCI D. Orthopartitions and Soft Clustering: Soft Mutual Information Measures for Clustering Validation [J].Knowledge-Based Systems,2019,180:51-61.
作者简介:聂斌(1972—),男,汉族,江西吉安人,教授,研究生导师,CCF会员(E200028664M),研究方向:数据挖掘、中医药信息学、中药学;靳海科(1999—),女,汉族,山西晋城人,硕士研究生,研究方向:数据挖掘;张玉超(1998—),男,汉族,重庆垫江人,硕士研究生,研究方向:数据挖掘;郑学鹏(1997—),男,汉族,广东汕尾人,硕士研究生,研究方向:数据挖掘;陈星鑫(1999—),男,汉族,江西赣州人,硕士研究生,研究方向:数据挖掘;苗震(1997—),男,汉族,吉林辽源人,硕士研究生,研究方向:数据挖掘;李欢(1995—),女,汉族,江西萍乡人,助教,硕士研究生,研究方向:数据挖掘。

