


摘" 要:环路作为一种特殊的模体,在揭示图的结构特征方面发挥着不可或缺的作用,能够帮助人们深入理解图的结构特点,得出更有价值的结论和科学预测。因此,环路挖掘一直是图研究领域中的热点问题之一。文章紧扣环路挖掘问题的研究脉络,从静态图和动态图两个维度,对图上的环路挖掘算法进行了全面细致的梳理,同时选取其中部分经典算法以更直观的方式展开进一步对比分析,并列出了相关研究所涉及的数据集与其对应的下载链接,便于读者能够更便捷地获取所需资源,展开进一步的探索与研究。
关键词:图数据挖掘;有向图;时序图;环路
中图分类号:TP399" " " 文献标识码:A" 文章编号:2096-4706(2024)18-0033-06
Research Progress on Cycle Mining Algorithm for Complex Network Graphs
LIU Xiaoting
(School of Computer and Information Engineering, Henan University of Economics and Law, Zhengzhou" 450046, China)
Abstract: As a special motif, cycle plays an indispensable role in revealing the structural characteristics of graphs, which can help people deeply understand the structural characteristics of graphs and draw more valuable conclusions and scientific prediction. Therefore, cycle mining has always been one of the hot issues in the field of graph research. This paper closely follows the research context of cycle mining problems, comprehensively and meticulously sorts out the cycle mining algorithm on the graph from the two dimensions of static graph and dynamic graph. And it selects some of the classic algorithms to carry out further comparative analysis in a more intuitive way, and lists the datasets involved in related studies and their corresponding download links, so that readers can obtain the required resources more conveniently and carry out further exploration and research.
Keywords: graph data mining; directed graph; temporal graph; cycle
0" 引" 言
随着信息科技与互联网的高速发展,各行各业的信息量都呈现了爆炸性的增长趋势。图模型以为其强大的抽象能力,因可以有效表示不同实体以及它们之间的关系,而被国内外学者广泛研究和应用。
环路是图数据中常见的概念,即可以通过沿着边走的方式回到出发点,在大量的图分析应用中扮演着重要的角色。在推荐算法领域[1-2],用户的兴趣往往受他们社交圈子的影响。因此,推荐系统可以利用这种社交影响,通过分析用户的社交网络中的环路来预测他们可能感兴趣的内容或产品。在信息传播分析领域[3-4],环可以被用来描述社交媒体用户之间消息的传递。通过分析这些环路的大小和环路上的顶点特征等,可以帮助人们更好地了解消息传递的特性和传播行为。在城市交通网络领域[5-6],环可能代表着重复的车辆或人员乘坐。利用这种环路进行行人或车辆轨迹的识别和分析,可以为城市规划和道路安全提供有价值的信息。在经济金融领域[7-8],环可以用来检测多个账户之间的交易行为。如果一个由多个账户组成的环路,并且这些账户之间频繁转移资金,则可能存在欺诈行为。挖掘这些环路信息可以帮助有关部门及时发现类似不法行为。
1" 环路挖掘算法
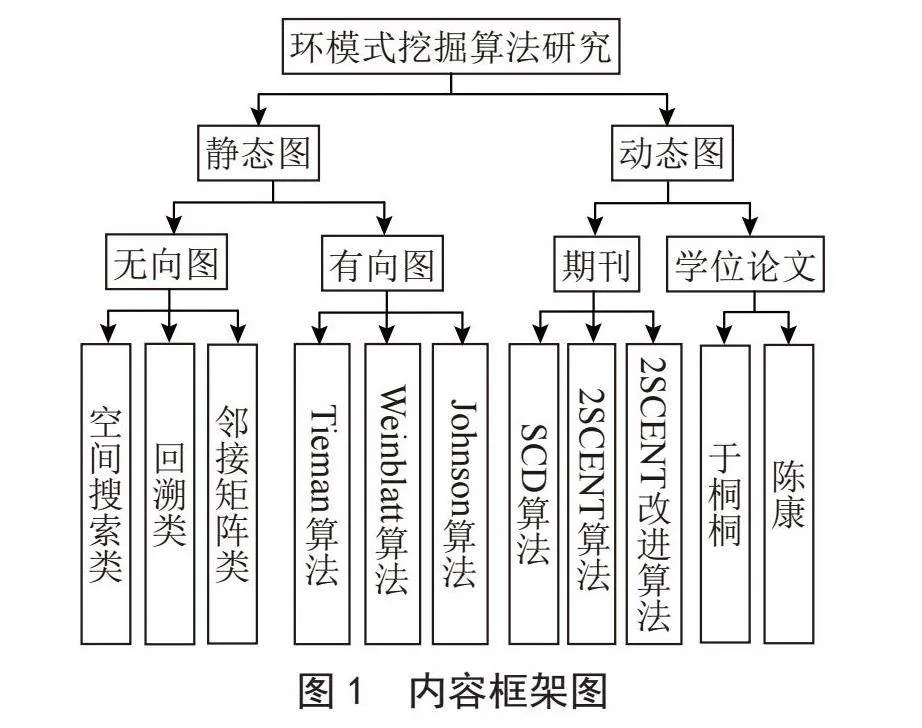
在现有的环路挖掘算法中,因为通过对整个图进行遍历就能找到任意两个顶点间的所有可达路径,故而遍历搜索成为最常采用的思想。搜索方式主要分为两类:一类是深度优先搜索(Depth-First-Search, DFS),另一类是广度优先搜索(Breadth-First-Search, BFS)。后期相关环路挖掘算法的研究大多在DFS或BFS的基础上,通过一定限制条件辅以剪枝实现。本小节根据环路挖掘问题的研究进程,按照静态图和动态图两方面对现有的典型环路挖掘算法进行分析总结,如图1所示。其中,静态图又从有向图和无向图两方面展开;由于现实生活中绝大多数的关系图均是有向图,故对无向图环路挖掘算法的相关研究,仅按照空间搜索类、回溯类和利用邻接矩阵类三种进行简要说明;最后是动态图,在1.3节中仍以时间为线索对时序图环路挖掘相关算法展开叙述;1.4节选取其中部分经典算法,对其展开进一步对比分析;1.5节中给出了相关研究所用数据集及其具体下载链接。
1.1" 基于静态有向图的环路挖掘算法
1.1.1" Tiernan算法
1970年,Tiernan[9]在静态有向图找到所有符合特定长度的简单环路方面,提出了一种新算法。该算法同样以深度优先搜索作为基础,从选定顶点作为起始点,开始顶点编号递增的顺序,依次将邻居顶点加入路径,再判断是否有环路形成。如果有环路形成,则输出环路信息,并移除该邻居路径,然后继续加入其他邻居顶点并判断是否有新的环路产生,直到依次判断完所有初始顶点。Tiernan在理论上证明了该算法的时间复杂度上限,并通过计算机依次在包含1~8个顶点的完全图上进行环路挖掘,结果表明Tiernan算法比较适用于在小规模的图上寻找环路,一旦图的顶点数超过7或者图的边数超过50,该算法将非常耗时。
1.1.2" Weinblatt算法
1972年,Weinblatt[10]提出了一种新的算法,将其适用范围拓展到更大的图。由于环路是由一组顶点和边组成,并且第一个顶点和最后一个顶点连接起来形成的,所以环路上的顶点必定同时具有出邻居和入邻居,若将只有出边和只有入边的顶点删除,那么就能有效减少后续对非必要顶点的无效搜索,提高搜索效率。因此,Weinblatt算法在进行搜索之前先对图进行预处理,删除出度和入度为0的顶点。接着在剩余的顶点中选择一个初始点,从该顶点出发搜索可行路径,碰到搜索过的顶点就回溯至上一个分支顶点,继续搜索从该顶点出发的其他未被搜索的路径。如果没有未搜索的顶点,就选择新的起始点,重复上述过程。在这个过程中,Weinblatt算法定义了TT(Trial Thread)列表,以此来保存当前初始顶点和正在搜索的路径。在回溯过程中,将经过的所有顶点和边从TT列表中删除,并判断留下的路径是否能形成环路。该算法在最坏情况下的时间复杂度为指数型,故并不适用于百万级顶点和边的图。
1.1.3" Johnson算法
1975年,Johnson[11]改进了Tiernan算法,提出了目前最有效的有向图环路挖掘算法。该算法首先利用Tarjin算法找出原始图的所有强连通分量(实现过程见算法1),然后在不同分量上依次搜索环路信息,显著提高了效率。算法采用DFS,记录顶点阻塞状态,并用三个数组A、Block和B存储搜索信息。从起始顶点s开始,按DFS规则添加路径顶点至数组A,并标记为阻塞,同时更新Block数组;若顶点i的所有出邻居均为阻塞,则将其放入B数组,停止搜索。继续添加顶点,若最后一个顶点v的邻居包含起始顶点s,则形成环路,输出。若顶点v的邻居已访问完毕,根据DFS法则退回上一级顶点v,继续搜索直至退回到顶点v的邻居顶点u。删除数组B中关于顶点v和u的指向关系,或继续搜索未访问的邻居。若起始点u的所有环路找到,删除顶点u,选定新起始顶点s1,递归执行Johnson算法,直至所有顶点的环路均被找到,算法终止。
算法1:Tarjan算法获取强连通分量
输入:起始顶点
输出:强连通分量SCC
1) Void tarjin(int s)
2) {
3) Stack。push(S);" " " nbsp; " " " " " "//把顶点S压入栈中
4) Visit[S]=1;" " " " " " " " " " " //表明节点S在栈中
5) dfn[S]=Low[S]=++flag;" " " "//初始化时间戳及先祖地位
6) For(T属于S的子节点) {" " " " " //遍历S所有的子节点
7) If(Visit[T]==0) {" " " " " " " //如果T 不在栈中
8) Tarjin(T);" " " " " " " "//继续向下搜索
9) Low[S]=min(Low[S],Low[T]) }" " " " "//更新节点S的先祖地位
10) Else if (Visit[T]==1) {" " " " " " //节点S处于栈中
11) Low[S]=min(Low[S],dfn[T]) }" " " " "//更新节点S的先祖地位
12) If(Low[S]==dfn[S]) {" " " //如果节点S先祖是自身,那么它就是一个SCC的ROOT
13) Do{
14) Pop T;" " " " " "//弹出T
15) Visit[T]=2;" " " "//表示T节点已经进入过并弹出
16) T=stack。pop;}" " "//更新T
17) While(S != T) } //一直弹到该强连通分量的ROOT为止,弹出节点便是一个SCC
18) }
19)}
1.2" 基于静态无向图的环路挖掘算法
静态有向图上的环路枚举算法中,表现最优的仍是Johnson算法,然而在面向无向图展开环路枚举时,Ferreira等[12]在2013年提出了比Johnson算法表现更优的算法,该算法令C(G)为图G上的所有环路,c为C(G)中每一条环路的边的数量,则Ferreira算法所需的时间为O(m+∑c∈C(G)c)。其中,O(m)是读图所必需的时间,而O(∑c∈C(G)c)是输入环路所必须的时间。因此,该算法是渐进最优的。除此之外,以往学者对无向图环路挖掘的相关研究,大致可分为空间搜索算法、回溯类算法和借助邻接矩阵三类,下面依次对其简要叙述:
1)空间搜索算法。根据这种方法,在适当的搜索空间中查找循环。在无向图的情况下,环路向量空间[13]被证明是最有希望的选择:从这个空间的一个基上计算所有向量,并测试它们是否是一个环路。自论文[14]中引入算法以来,已经提出了许多算法。然而,这些算法的复杂度与向量空间的维数成指数关系,因此,也与n成指数关系。
2)回溯类算法。通过这种方法,所有路径都是通过回溯生成的,并且对于每个路径都要测试它是否是一个环路。第一批算法之一是论文[15]中提出的算法,但它的η是指数的。通过添加一个简单的剪枝策略,该算法在论文[16]被修改:通过添加一个简单的剪枝策略,使其能在O(nm(η + 1))时间内列出所有的循环。论文[17-18]中提出了进一步改进,从而产生了O((η + 1)(m + n))时间的算法,这种算法同时适用于有向图和无向图。
3)借助邻接矩阵类算法。这种方法使用了所谓的可变邻接矩阵,即连接两个顶点的边的正式和。这个矩阵的p次幂的非零元素是长度为p的所有游动的和。因此,为了计算所有的循环,需要计算变量邻接矩阵的n次幂。事实上这种方法因为不是简单的遍历而不是很有效。基于这种方法的算法[19]基本上只在避免考虑既不是路径也不是循环的行走方式上有所不同。
1.3" 基于动态时序图的环路挖掘算法
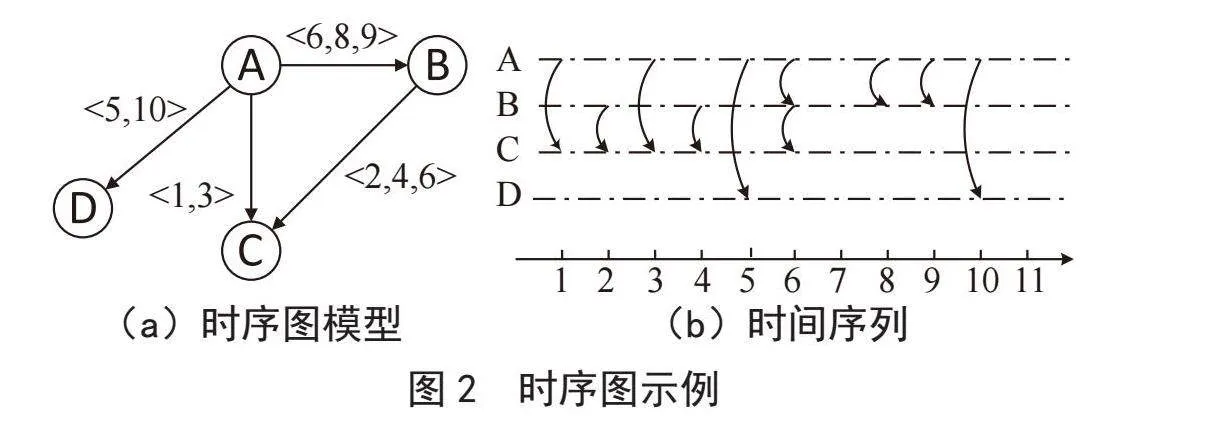
时序图(Temporal graph),即给定时序图G′(V,E),其中,V和E分别是图G′中的一组顶点和一组边。对任一条边e∈E,用四元组(u,v,t,α)表示,其中u,v是图G′中任意两个顶点,t是开始时间,α是从顶点u到顶点v的所耗费的时间,则从顶点u到顶点v的结束时间为t+α。边e的开始时间为t(e),遍历时间为α(e),也即边e的激活时间为[t,t+α]。时序图模型如图2(a)所示,图2(b)为其对应的时间序列,即各个时刻边的激活情况。
上述几种算法均是在静态有向图上的环路挖掘研究,然而近年来随着时序图的兴起,国内外学者开始研究动态时序图上环路枚举问题。
1.3.1" SCD算法
2017年时,Kumar等人首次将环路挖掘研究从静态有向图扩展至时序图,提出了较为传统的时序环路挖掘算法[20](Simple Cycle Detection Algorithm, SCD),该算法使用简单时序环路及其数量分布来展示信息的流动。具体来说,通过遍历窗口中所有可能的时序路径,以枚举方式寻找时序环路(实现过程见算法2)。该算法背后的关键思想是维护给定窗口长度ω的所有有效时间路径的列表(L),记录当前形成的时序路径,并将新的节点追加到之前的路径上,直到形成一个环路。时间路径p=,如果t-t1<ω,则认为在时间戳t内有效。如果路径无效,将它从列表中删除,因为它在后续的搜索中永远无法扩展以形成有效的循环。对于每个交互(u,v,t)所有以u结尾且不包含v的有效路径被扩展以创建一个新的时间路径。此外,从v到u的所有有效简单路径形成一个循环,其中v作为交互(u,v,t)的根节点。该算法虽然这种算法简单易懂,易于实现,但是它并不适用于大型图形,因为当路径数量增多时,算法会消耗过多的内存。
算法2: SCD算法
输入: 时间窗口ω、边ε
输出: 所有简单环路
1) L←{ }
2) for do,按时间递增顺序
3) for p=" do
4) " "if" then
5) " " " if" then
6) " " " " " 输出
7) else ifthen
8)
9) " "else
10)
11)
1.3.2" 2SCENT算法
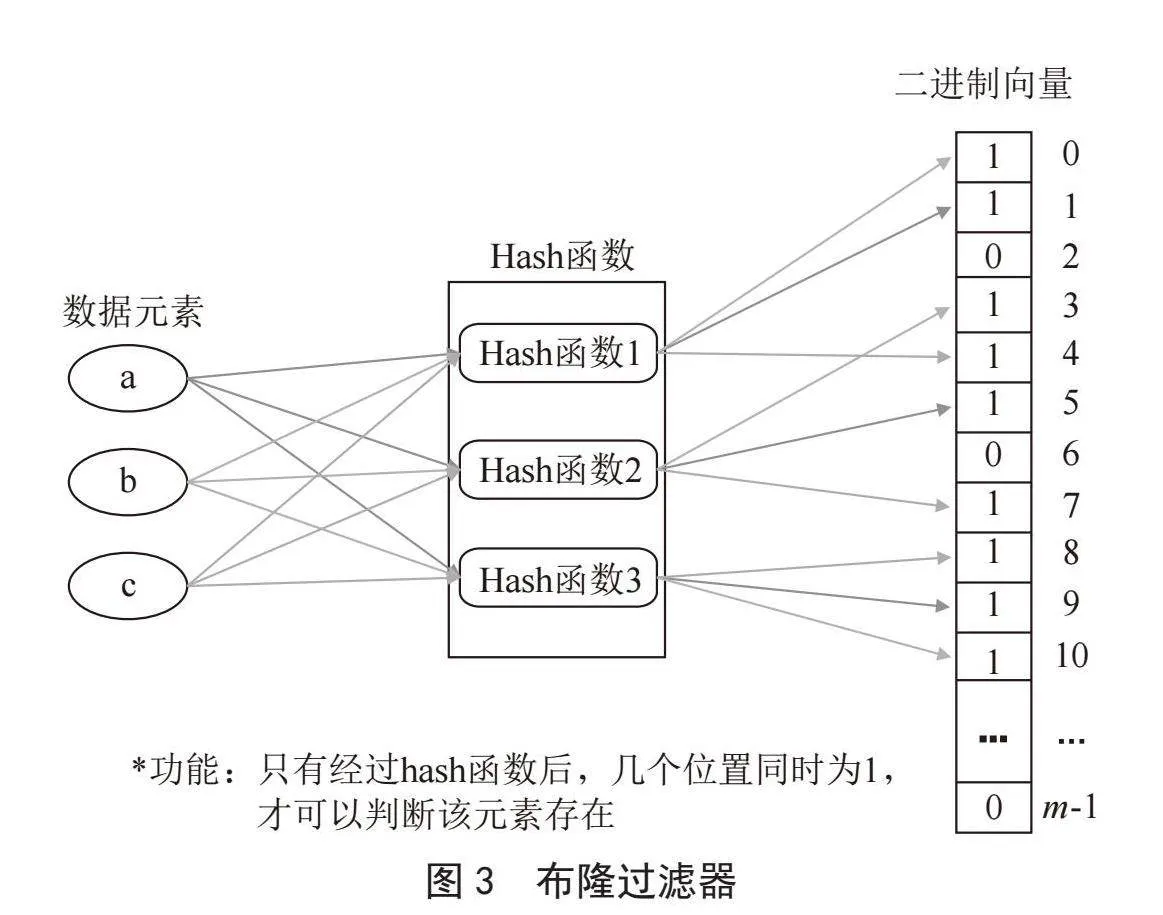
2018年时,Kumar等人提出一种时序递增的环路枚举算法2SCENT[21],也是目前为止最快的时序环路枚举算法。该算法借鉴Johnson算法的思想,属于Johnson算法在时序图上的衍生。相比于2017年提出的SCD朴素算法,2SCENT算法的时间效率提升了300倍以上,并且能够处理更大规模的图。2SCENT算法分为源检测阶段和受约束的深度优先搜索阶段两部分。在第一个阶段,找到所有可能是环路根节点的顶点信息作为候选节点,同时获得包含环路顶点、开始时间、结束时间、候选节点集合在内的四元组信息。这一阶段采用了布隆过滤器用于表示允许查询的集合,如图3所示。因为布隆过滤器不像链表查询一样需要逐个遍历,而是像数组查询,通过直接取下标即可获得所需结果。因此,引入了布隆过滤器进行信息处理后,该算法的效率大大提升,同时可以适应更大规模的图。在第二个阶段,根据第一阶段得到的候选集信息展开深度优先搜索。为减少非必要的搜索,该算法通过引入“关闭时间”的概念实现剪枝;同时使用“路径束”对有多重边和高度重复活动特点的网络进行搜索,进一步提高算法效率。
1.3.3" 2SCENT算法改进算法
2020年,潘敏佳[22]等人在2SCENT算法的基础上,通过在剪枝过程增加“最小长度”这一限制条件对环路进行约束,减少深度优先搜索的深度,最后得到限定长度且满足时序递增的环路。该算法因在加入了长度约束条件,使得在第一阶段中候选元组的数量大幅度减少,搜索效率进一步提升;此外,在对某一长度范围内的环路及逆行检索时,该算法所需的时间更短,且这种差距会随着图规模的增大而越发显著。然而,该算法在搜索过程中,仍然存在重复遍历同一路径的问题,若能解决这一弊端,算法效率将再次得到提升。
1.3.4" 基于矩阵代数运算与广度优先搜索相结合的图算法
2022年,于桐桐[23]在其论文中对有限长的简单环路枚举问题进行了研究。他进行了关于有向图强连通分量的图代数计算,并提出了一种基于矩阵代数运算与广度优先搜索相结合的图算法。该算法首先将图分割成若干个强连通分量,以减少无效搜索量。与经典算法以及潘敏佳等人的算法相比,该作者将图算法的计算对象转换成了邻接矩阵,从而实现多个矩阵的同时运算,提高检索效率。同时,针对基于栈的深度优先搜索只适用于小规模图的缺陷,提出了基于队列的融合搜索,将深度优先搜索与多层广度优先搜索相结合,极大地减少计算时间。然而,这也是该算法的局限性所在,因为该算法的多层深度优先搜索方法仅适用于较短环路的枚举,无法解决枚举所有简单环路的问题。
1.3.5" 时序图强连通分量
2023年,陈康[24]在其发表的论文中首次提出了时序图强连通分量的概念。针对时序图环路的特点,作者构建了以边为基础的新的图存储索引结构,建立了边与边之间的直接关系。这一索引结构能够通过预计算来剪枝大部分计算空间,可用于解决时序图下的简单环路枚举问题,同时为解决其他时序图相关问题提供了良好的基本思路。在边候选集索引的基础上,作者提出了利用优先队列进行边的反向源点可达性计算方法。该方法具有较低的时间复杂度,通过理论分析与实验验证,证明了其巨大的剪枝能力,可以显著提升后续环路枚举过程的运行效率,解决了环路候选集合过滤的痛点问题。
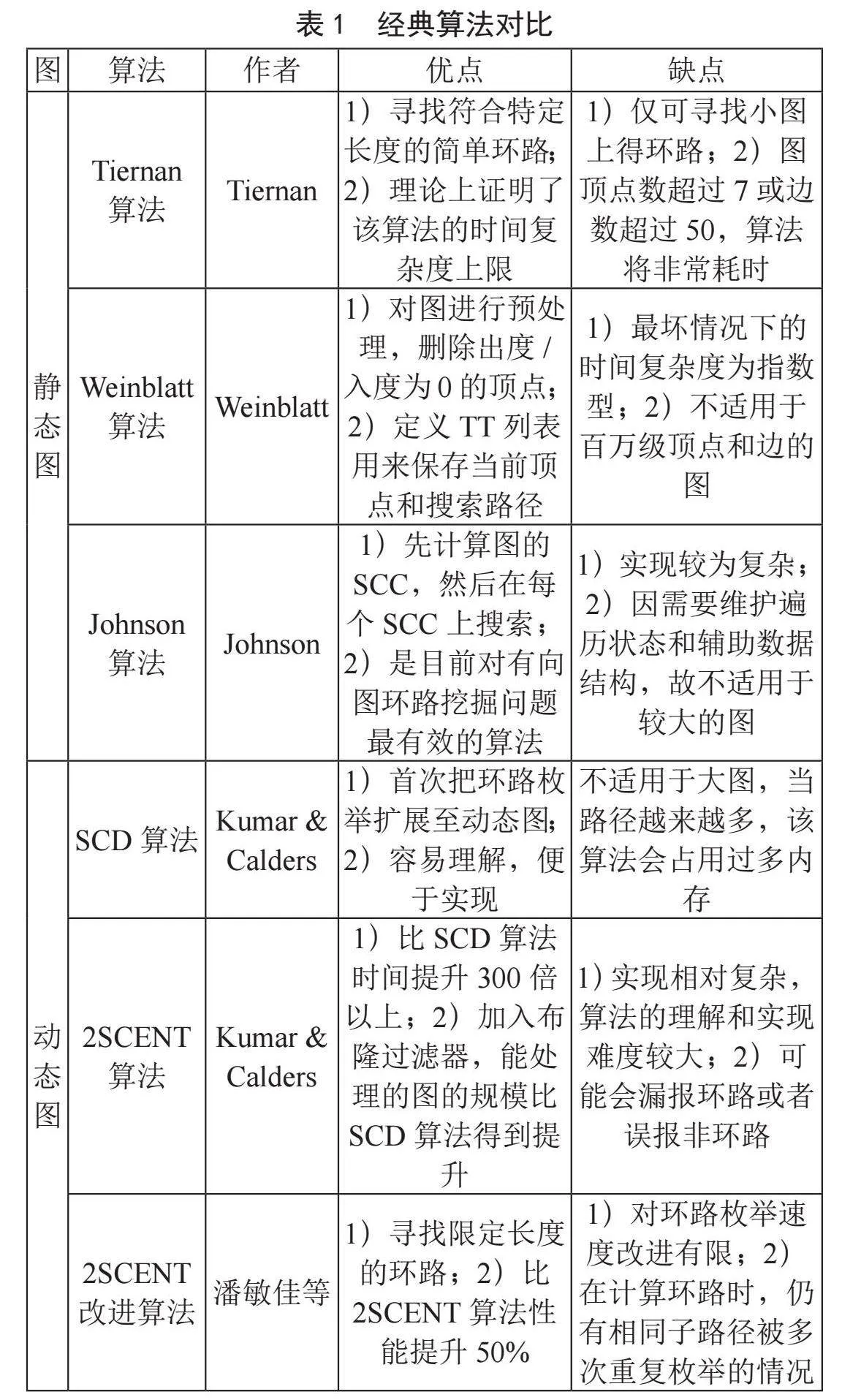
1.4" 经典算法对比
上一节从静态图和动态图两方面对现有的环路挖掘算法的思想进行了简要概述,本节选取其中具有代表性的算法,通过更直观的形式对各个算法的优缺点进行对比分析,以便读者可以对以下经典算法有更深入的理解,详细情况如表1所示。
1.5" 相关数据集
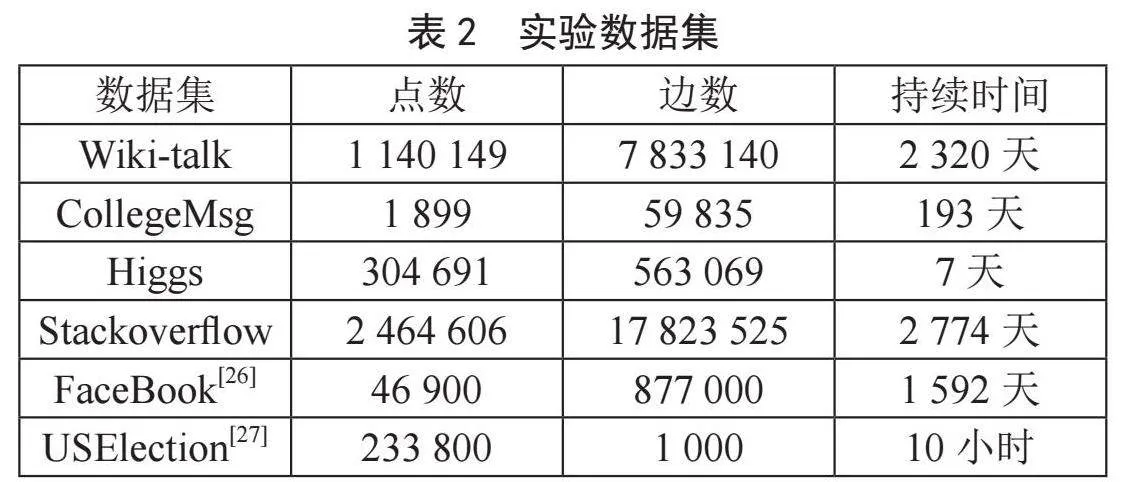
本小节详细介绍了环路挖掘相关论文中用到数据集的具体情况,并给出了各个数据集对应的下载链接,如表2所示(其中前4个数据集均来自SNAP大型网络数据集网站[25])。具体内容如下:
1)Wiki-talk。该数据集记录了Wikipedia用户修改其他用户的讨论页的行为。
2)CollegeMsg。该数据记录了加州大学欧文分校在线社交网络中的信息发送情况。
3)Higgs-twitter。该数据集记录了twitter上用户的信息往来行为(Higgs数据集于2015年更新,故下载链接数据与论文中摘录的数据有些许出入)。
4)Stack-overflow。该数据集记录了stackoverflow网站上的用户往来行为。
5)FaceBook。该数据集记录了FaceBook网站上的用户往来行为。
6)USElection。该数据集记录了美国历史选举结果。
2" 结" 论
大数据时代的悄然来临,掀起了人们对图模型的研究热潮,环路因其在推荐算法、路网规划和金融反欺诈等领域的广泛应用,成为备受瞩目的研究问题之一。本文按照时间顺序,从静态图和动态图两方面,对现有的环路挖掘算法的原理进行了总结,选取其中具有代表性的算法展开了进一步的对比分析,并给出了相关研究所用的数据集及其下载链接,希望能对图研究领域的初学者有所帮助,尽可能推动该问题的研究与发展。
参考文献:
[1] XIA L H,HUANG C,ZHANG C X. Self-Supervised Hypergraph Transformer for Recommender Systems [J/OL].arXiv:2207.14338 [cs.IR].(2022-07-28).https://arxiv.org/abs/2207.14338.
[2] WANG C Y,YU Y Q,MA W Z,et al. Towards Representation Alignment and Uniformity in Collaborative Filtering [J/OL].arXiv:2206.12811 [cs.IR].(2022-06-26).https://arxiv.org/abs/2206.12811.
[3] 胡长军,许文文,胡颖,等.在线社交网络信息传播研究综述 [J].电子与信息学报,2017,39(4):794-804.
[4] 李洋,陈毅恒,刘挺.微博信息传播预测研究综述 [J].软件学报,2016,27(2):247-263.
[5] RUSEK K,SUÁREZ-VARELA J,ALMASAN P,et al. RouteNet: Leveraging Graph Neural Networks for Network Modeling and Optimization in SDN [J].IEEE Journal on Selected Areas in Communications,2020,38(10):2260-2270.
[6] XIE Z Y,HUANG Y H,FANG G Q,et al. RouteNet: Routability Prediction for Mixed-Size Designs Using Convolutional Neural Network [C]//2018 IEEE/ACM International Conference on Computer-Aided Design(ICCAD).San Diego:IEEE,2018:1-8.
[7] ALTMAN E,BLANUŠA J,NIEDERHÄUSERN L V,et al. Realistic Synthetic Financial Transactions for Anti-Money Laundering Models [J/OL].arXiv:2306.16424 [cs.AI].(2023-06-22).https://arxiv.org/abs/2306.16424.
[8] WEN D,HUANG Y L,ZHANG Y,et al. Efficiently Answering Span-Reachability Queries in Large Temporal Graphs [C]//2020 IEEE 36th International Conference on Data Engineering(ICDE).Dallas:IEEE,2020:1153-1164.
[9] TIERNAN J C. An Efficient Search Algorithm to Find the Elementary Circuits of a Graph [J].Communications of the ACM,1970,13(12):722-726.
[10] WEINBLATT H. A New Search Algorithm for Finding the Simple Cycles of a Finite Directed Graph [J].Journal of the ACM,1972,19(1):43-56.
[11] JOHNSON D B. Finding all the Elementary Circuits of a Directed Graph [J].SIAM Journal on Computing,1975,4(1):77-84.
[12] ETIENNE B,RUI F,ROBERTO G,et al. Optimal Listing of Cycles and St-paths in Undirected Graphs [C]//Proceedings of the 24th Annual ACM-SIAM Symposium on Discrete Algorithms. Society for Industrial and Applied Mathematics,2013:1884-1896.
[13] BROWN R. Singular Homology Theory (Graduate Texts in Mathematics, 70) [J].Bulletin of the London Mathematical Society,1981,13(4):373-374.
[14] WELCH J W.A Mechanical Analysis of the Cyclic Structure of Undirected Linear Graphs [J].Journal of the ACM (JACM),1966,13(2):205-210.
[15] TIERNAN J C. An Efficient Search Algorithm to Find the Elementary Circuits of a Graph [J].Communications of the ACM,1970,13(12):722-726.
[16] TARJAN R E. Enumeration of the Elementary Circuits of a Directed Graph [J].SIAM Journal on Computing,1973,2(3):211-216.
[17] JOHNSON D B. Finding all the Elementary Circuits of a Directed Graph [J].SIAM Journal on Computing,1975,4(1):77-84.
[18] SZWARCFITER J L,LAUER P E. A Search Strategy for the Elementary Cycles of a Directed Graph [J].BIT Numerical Mathematics,1976,16(2):192-204.
[19] PONSTEIN J. Self-avoiding Paths and the Adjacency Matrix of a Graph [J].SIAM Journal on Applied Mathematics,2006,14(3):600-609.
[20] KUMAR R,CALDERS T. Finding Simple Temporal Cycles in an Interaction Network [C]//Proceeding of the Workshop on Large-Scale Time Dependent Graphs, Co-Located with the European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases.Macedonia:CEUR,2017:3-6.
[21] KUMAR R,CALDERS T. 2Scent: An Efficient Algorithm to Enumerate All Simple Temporal Cycles [J].Proceedings of the VLDB Endowment,2018,11(11):1441-1453.
[22] 潘敏佳,李荣华,赵宇海,等.面向时序图数据的快速环枚举算法 [J].软件学报,2020,31(12):3823-3835.
[23] 于桐桐.时序网络中环路检测算法的研究 [D].济南:山东大学,2022.
[24] 陈康.基于时序图的简单环路枚举研究 [D].广州:广州大学,2023.
[25] LESKOVEC J,KREVL A. SNAP Datasets: Stanford Large Network Dataset Collection [EB/OL].[2024-01-26].https://snap.stanford.edu/data.
[26] MISLOVE A. Social Computing Research a MPI-SWS [EB/OL].[2024-01-26].https://socialnetworks .mpi-sws.org/datasets.html.
[27] TUNGGUZ B. Kaggle [EB/OL].[2024-01-26].https://www.kaggle.com/tunguz/us-elections-dataset.
作者简介:刘笑婷(1996—),女,汉族,河南洛阳人,硕士在读,研究方向:图数据挖掘与分析。