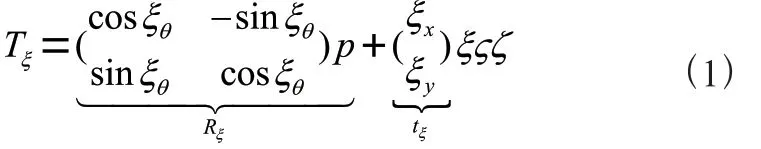




摘" 要:基于阵列流形分离(MST)的共形阵列空间谱估计技术,采用快速傅里叶变换(FFT)来降低谱搜索的计算复杂度,但是在该方法中,空间谱搜索的俯仰角和方位角均为0~360°,存在计算搜索冗余问题。针对共形阵列空间谱估计问题,提出基于联合阵列流形分离技术和频谱细化技术的空间谱估计技术,避免计算搜索冗余问题,相比阵列流形分离技术计算复杂度显著降低。采用一个32阵元球面共形阵列进行计算机仿真,验证了所提出方法的估计性能和计算复杂度。
关键词:DOA估计;MUSIC算法;频谱细化技术;Chirp-Z变换;低复杂度;
中图分类号:TN911.7" " " 文献标识码:A" " " 文章编号:2096-4706(2024)18-0010-06
Low-complexity DOA Estimation Method Based on Manifold Separation and Spectrum Refinement Technique
JIANG Keliang, HUANG Zhijiang, XIE Nan
(Institute of Electronic Engineering, China Academy of Engineering Physics, Mianyang" 621900, China)
Abstract: Conformal array spatial spectrum estimation technique based on MST uses FFT to reduce the computational complexity of spectral search, but in this method, elevation angle and azimuth angle of the spatial spectrum search are both 0°~360°, and there is a problem of computational search redundancy. To address the problem of conformal array spatial spectrum estimation, spatial spectrum estimation technique based on joint MST and spectrum refinement technique is proposed to avoid computational search redundancy problem, reducing the computational complexity significantly compared to MST. A 32-element spherical conformal array is used for computer simulation to verify the estimation performance and computational complexity of the proposed method.
Keywords: DOA estimation; MUSIC algorithm; spectrum refinement technique; Chirp-Z transform; low-complexity
0" 引" 言
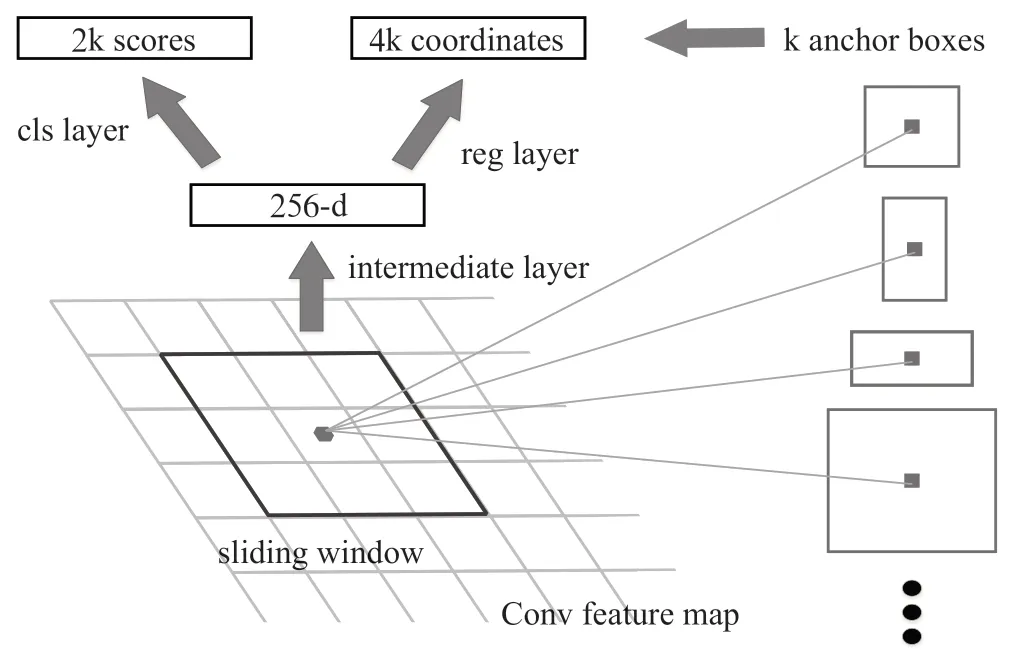
波达方向(Direction of Arrival, DOA)估计是阵列信号处理中一个普遍的问题,需要通过分析阵列天线之间的相位差来估计目标方向。美国学者Schmidt等人于1979年开创性得提出多重信号分类(Multiple Signal Classification, MUSIC)算法[1],推动了DOA估计算法的进步。MUSIC算法可以直接从一维推广到二维,运算量巨大使得二维MUSIC算法有着局限性。为了减少二维DOA估计算法的计算量,人们研究了许多方法,例如流形分离技术[2](Manifold Separation Technique, MST)。2018年Jie Zhuang等人提出利用流形分离技术将二维MUSIC谱估计公式转换为标准的二维离散傅里叶变换(2D DFT)形式,再利用二维快速傅里叶变换(2D FFT)算法就可以有效地计算出二维空间频谱,还提出高并行度的算法,不仅减轻了计算负担,还易于硬件实现[3]。
当再入飞行器以大于10马赫的速度返回地球大气层时,会在地球上空一定高度区间中发生与地面联络失效或中断的现象,即为黑障现象[4-5]。2023年间返回的神州十五、十六号载人飞船返回舱均出现了长达数十秒甚至数百秒的黑障现象。黑障区非常危险,如果地面不能实时跟踪测量返回舱的位置,容易出现返回舱偏离预定的着陆区域,延误对返回舱的及时搜索和救援。在返回舱穿过黑障区后,由于飞行速度较快和落地前时间有限,就需要地面的雷达系统立马捕获目标并稳定跟踪,这就对DOA估计的时性提出更高的要求。
在2D FFT中,俯仰角的谱搜索范围是[0,2π),在三维坐标系中,只需要对[0,π]的俯仰角范围进行谱搜索,就能实现全空域搜索,其余范围包含的都是重复的信息。而且对于一些特殊场景的应用,例如对突破黑障区的再入飞行器的探测,结合先验信息仅需对有限角度围进行搜索,从而进一步降低搜索范围。本文将用线性调频z变换[6-7](CZT)有选择性地取代普通的二维傅立叶变换,避免谱搜索计算中冗余的部分,减少谱搜索的计算量和时间,以实现对目标初步的快速捕获。
1" 基于流形分离与FFT的2D MUSIC算法
流形分离技术,是用二维傅立叶级数来近似阵列导向矢量的方法。利用傅立叶级数的展开,将阵列导向矢量分解成一个采样矩阵和两个范德蒙德结构向量乘积的形式:
(1)
其中,为阵列导向矢量,θ为俯仰角,0°表示指向天顶,180°表示指向地下,ϕ为方位角角,G为采样矩阵,ε为误差,L为天线数量,向量是由两个范德蒙德向量组成的傅立叶基:
(2)
(3)
(4)
其中为克罗内克积(Kronecker product),为转置运算。可以看出,只依赖于波场,当模数M足够大时,误差ε就小到可以忽略;采样矩阵 只依赖于阵列天线的构造及特性。
用二维EADF(Effective Aperture Distribution Fu-nction)来近似采样矩阵,采样矩阵的计算过程见文献[8-9]。将流形分离技术的公式(忽略误差)带入MUSIC算法的空间谱计算函数,其中为噪声子空间特征向量,得到的空间谱函数变为:
基于MUSIC技术的空间谱定义为:
(5)
其中为噪声子空间特征向量,将式(1)代入式(5),得到:
(6)
其中和为范德蒙德结构向量,为共轭转置运算,矩阵为系数矩阵。
要计算系数矩阵C,首先要将矩阵写成分块矩阵的形式,每个子矩阵都是一个M行M列的矩阵。然后计算沿所有2M-1条对角线的子矩阵的和,Di为第i条对角线的元素之和,这里分块矩阵左下角的子矩阵记为第1条对角线,主对角线为第M条对角线。再计算沿Di的所有条对角线的元素之和,Di的第q条对角线的元素之和,即为C的第(i,q)个元素[8-9]。
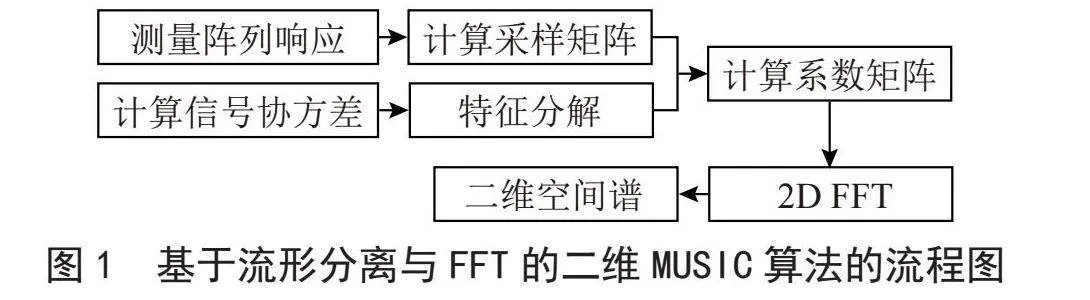
一般情况下,矩阵C的数值大部分集中在中心部分,只保留中心部分用于后续计算,Mi的取值根据Doron等人提出的经验法则Mi≈κR,κ为信号波数,R为阵列天线的阵元与系统原点之间的最大距离[10]。再将Ci补零成,其中N是2的幂,且N大于2Mi+1。之后,对CN进行2D DFT即可得到空间谱,采用FFT算法又可以很快地计算出N点DFT值,还便于硬件实现,这就是基于流形分离与FFT的二维MUSIC算法,算法流程如图1所示。
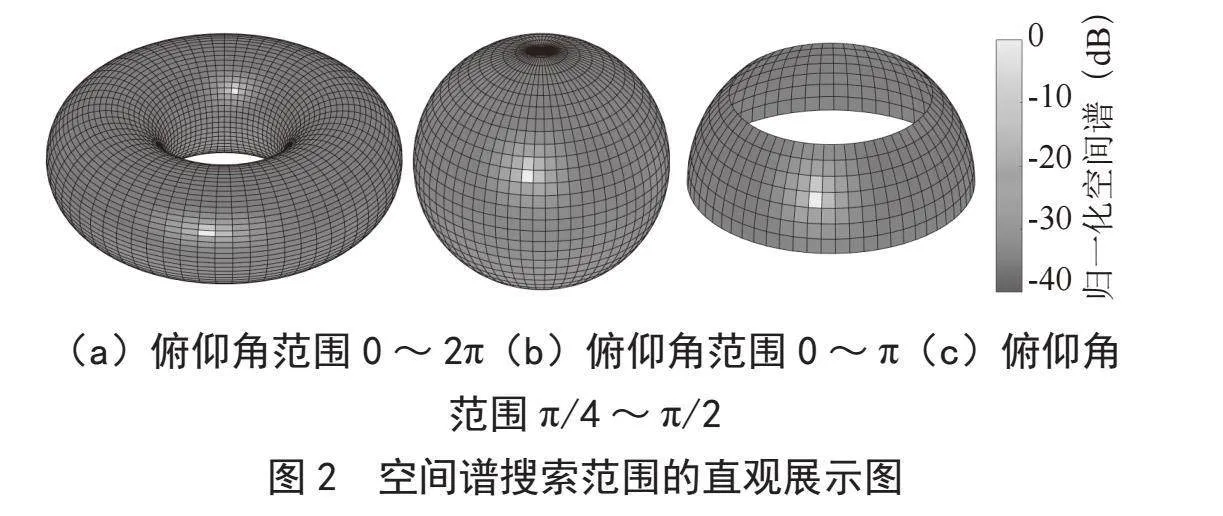
假设信源方位角的俯仰角分别为220°、60°,上述算法中的2D FFT过程必须要在θ∈[0,2π)和ϕ∈[0,2π)区间上计算空间谱,如图2(a)所示,方向角和俯仰角都是在球坐标系中,根据球坐标系的特性可知,俯仰角区间有一半是多余的,也就是说空间谱的结果中有一半是重复的,这就导致图2(a)的空间谱中有两个峰值出现,这两个峰值点在三维空间中表示的方位相同。经典MUSIC算法仅需要计算在θ∈[0,π)和ϕ∈[0,2π)区间的空间谱,如图2(b)所示。在许多实际应用场景中不需要计算整个单位圆上Z变换的取样值,例如,对于地对空雷达等特殊应用场景,通常只关心特定方向的空间谱,而不需要对地面以下或部分头顶区域进行空间谱搜索。此外,如果已知目标的大致方向,那么只需在一定范围内进行空间谱搜索。在这样的应用场景中,使用频谱细化算法就可以实现只对部分角度范围进行谱搜索,例如只计算θ∈[π/4,π/2)和ϕ∈[0,2π)区间的空间谱,如图2(c)所示。
2" 基于频谱细化技术的低复杂度DOA估计方法
基于流形分离与FFT的2D MUSIC算法在空间谱搜索计算中仍然存在冗余的问题。为了改善这一问题,引入了频谱细化分析方法,并将其与基于流形分离和FFT的2D MUSIC方法相结合。具体而言,就是把该DOA估计方法中2D FFT过程中的两个维度的FFT中的某个维度或两个维度的传统FFT替换成频谱细化FFT,需要根据空间谱搜索所需的范围进行选择,缩小空间谱搜索的范围,减少冗余计算,降低空间谱搜索计算量。这一改进使得算法更适应不同应用场景下的实时计算需求。
2.1" 基于CZT的2D MUSIC算法
常用的频谱细化技术包括Chirp-Z变换法、复调制Zoom-FFT方法、相位补偿Zoom-FFT、Yip级联Zoom-FFT方法等方法[11-12]。这些方法在处理精度、细化能力、计算效率以及适用场景等方面各有不同,频谱细化方法的具体选择应根据应用场景和实际需求来决定。本文主要运用Chirp-Z变换法实现。
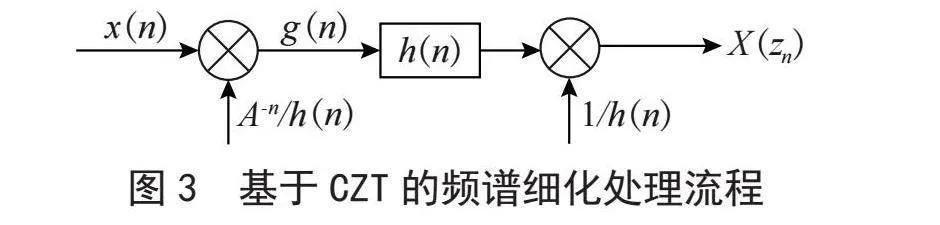
Chirp-Z变换,也就是线性调频z变换,简称CZT,是对z变换采用螺旋线采样,是一种适合于上述需求的变换。基于CZT的频谱细化处理流程如图3所示,其中,zk=AW -k,k=0,…,M-1,,A0为起始取样点的半径,θ0为起始取样点z0的相角, ,ϕ0为相邻两点间的等分角,W0为螺旋线的伸展率[12]。
基于CZT的2D MUSIC算法,就是把之前删减再补零后的矩阵CN某个维度或两个维度的FFT换成CZT,根据空间谱搜索所需的范围进行选择。CZT过程中可用循环卷积的方式计算线性卷积,但需要先将序列延长至适合循环卷积的长度,再用计算两序列的FFT序列乘积的IFFT的方式计算循环卷积,就能用FFT实现CZT的快速计算。这里使用CZT的目的是减少空间谱搜索范围,只保留z变换某一段圆弧上的采样点,并不改变采样点轨迹和采样点的间隔。令A0=1和W0=1,CZT会从螺旋线采样变成一段单位圆上圆弧的采样。令ϕ0=2π/N,即,CZT就能与FFT拥有相同的采样间隔。
基于CZT的DOA估计方法的算法主要步骤分为离线处理和在线处理。
离线处理:
1)测量每个阵元若干方向的阵列响应,并通过矩阵操作得到周期校正矩阵。
2)对不同阵元的周期校正矩阵进行2D FFT,保留中心部分,向量化后依次拼接,得到采样矩阵G。
在线处理:
1)采用接收信号快拍数据计算协方差矩阵。
2)对协方差矩阵特征分解计算得到噪声子空间。
3)计算矩阵,写成分块矩阵的形式,通过两次所有对角线方向求和得到系数矩阵C,只保留中心的2Mi+1行和列,得到矩阵C。
4)根据角度限制对Ci每行进行相应的CZT变换:
首先,根据应用场景选择合适的采样点起始相角θ0、间隔ϕ0和点数MC,计算h(n)并延长至LC长序列,LC为2的幂且LC≥N+MC-1,计算h(n)的FFT。
其次,对矩阵Ci的每一行补零为N长序列,计算g(n)并补零至LC长序列,并对每个LC长序列进行FFT处理。
再次,将每行g(n)的FFT与h(n)的FFT相乘后再做IFFT,截取对应的MC长序列。
最后,将得到的每行的MC长序列分别与1/h(n)相乘,得到每行的CZT。
5)如果还需要限制方位角的搜索范围,则对上一步的结果再按照步骤3)的方式进行每列的CZT,即可得到空间谱;如果需要360°的方位角搜索范围,则对步骤3)结果计算每列的FFT,即可得到空间谱。
2.2" 算法复杂度分析
本文提出的用于计算二维空间谱的基于CZT的DOA估计方法,在同一个天线阵列的使用过程中,离线处理部分均只需运行一遍,该部分不在本次复杂度分析的范围中,主要考虑对算法实时性有影响的实时处理部分。基于CZT的算法的运算主要是矩阵运算,因此其加法运算的数量与乘法运算的数量大致相等。鉴于复数乘法运算在整个计算过程中占据了主导地位,这里将重点放在复数乘法运算数量上,来分析基于CZT的算法的计算复杂度。
基于CZT的算法实时处理部分复杂度分析:
步骤1:快拍数为Ns,信源数K,计算协方差矩阵杂度为O(KNs)。
步骤2:特征分解使用快速子空间分解技术,得到K维信号子空间特征向量,复杂度为O(KL2)[13]。
步骤3:使用文献[3]中求迹的方法计算矩阵Ct,计算每个元素都需要KL2+L2次复数乘法,又因为矩阵Ct具有对称特性,只需要大约四分之一的元素即可得到整个Ct,因此总共需要大约(1/4)×(2Mt+1)2×(KL2+L2)次复数乘法,又因为L远大于K所以复杂度为。
步骤4:1)因为LC≥N+MC-1是2的幂,且1<MC≤N,所以取LC=2N,长度为2N的FFT需要N(logN+1)次复数乘法,复杂度为O(NlogN)。2)计算每行的g(n)需要2Mt+1次复数乘法,长度为2N的FFT需要N(logN+1)次复数乘法,2N行的复杂度为。3)每行相乘需要2N次复数乘法,长度为2N的IFFT需要N(logN+1)次复数乘法,2N行的复杂度为O(MtNlogN)。4)需要(2Mt+1)×MC次复数乘法,复杂度为O(MCMt)。
步骤4:的复杂度为O(NlogN+MtNlogN++MCMt)。
步骤5:L=10选择FFT,计算MC列长度为LC≥N+MC-1的FFT需要MC×(N/2)×logN次复数乘法,复杂度为O(MCNlogN)。因此该算法总复杂度为O(KL2+L2+(Mt+MC+1)NlogN++MCMt)。
为了将基于CZT的算法与基于FFT的2D MUSIC算法进行比较,还需进行基于FFT算法的复杂度分析:计算协方差矩阵杂度为O(KNs);快速子空间分解,复杂度为O(KL2);计算矩阵B总共需要L2(L-K)+L2M2+L2M4次复数乘法,复杂度为O(L2(L-K)+L2M2+L2M4);对大小为N×N的系数矩阵进行2D FFT总共需要N2logN次复数乘法,复杂度为O(N2logN)。基于FFT算法的总复杂度为O(L3+L2M2+LM4+N2logN)。而经典2D MUSIC算法复杂度为O(KNs+KL2+KLNaNe),其中Na、Ne分别为方位角、俯仰角方向的空间谱搜索点数,取值分别为N和N/2。
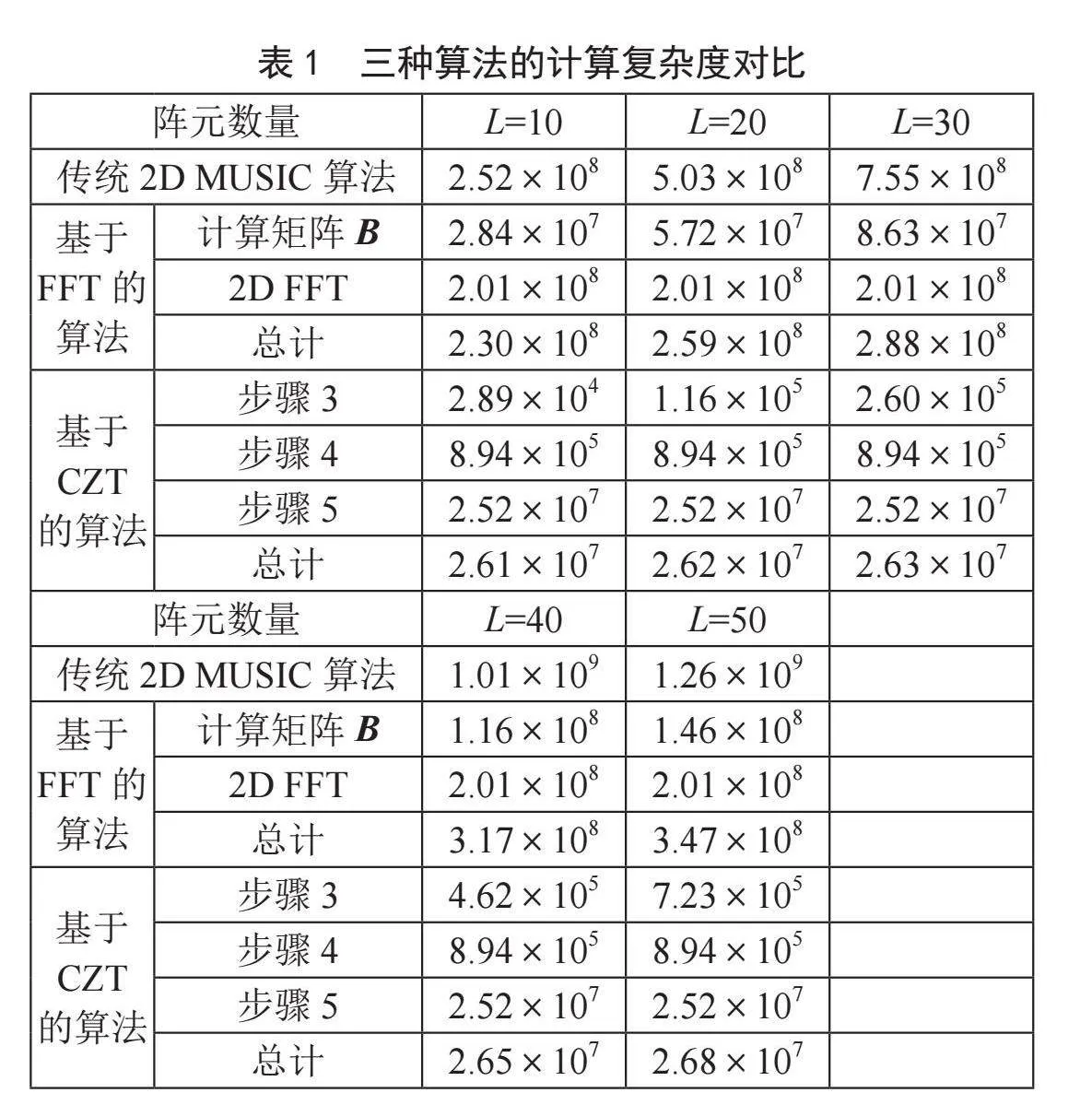
在表1中,以计算θ∈[π/4,π/2]和ϕ∈[0,2π)区间的空间谱为例,在不同阵元数量情况下,对基于CZT的算法、基于FFT的2D MUSIC算法以及经典2D MUSIC算法的算法复杂度进行比较。由于这三种方法特征分解复杂度均为O(KL2),且计算协方差矩阵杂度为O(KNs),所以在复杂度比较中不计算这两部分。这里主要考虑球面共形天线,阵列半径R=0.15 m,信源数K=3,快拍数为1 000,信号频率2.2 GHz。选择比经验法则略大的Mt≈2.5κR,这里取Mt=17,取M=41,N=4 096,MC=512。
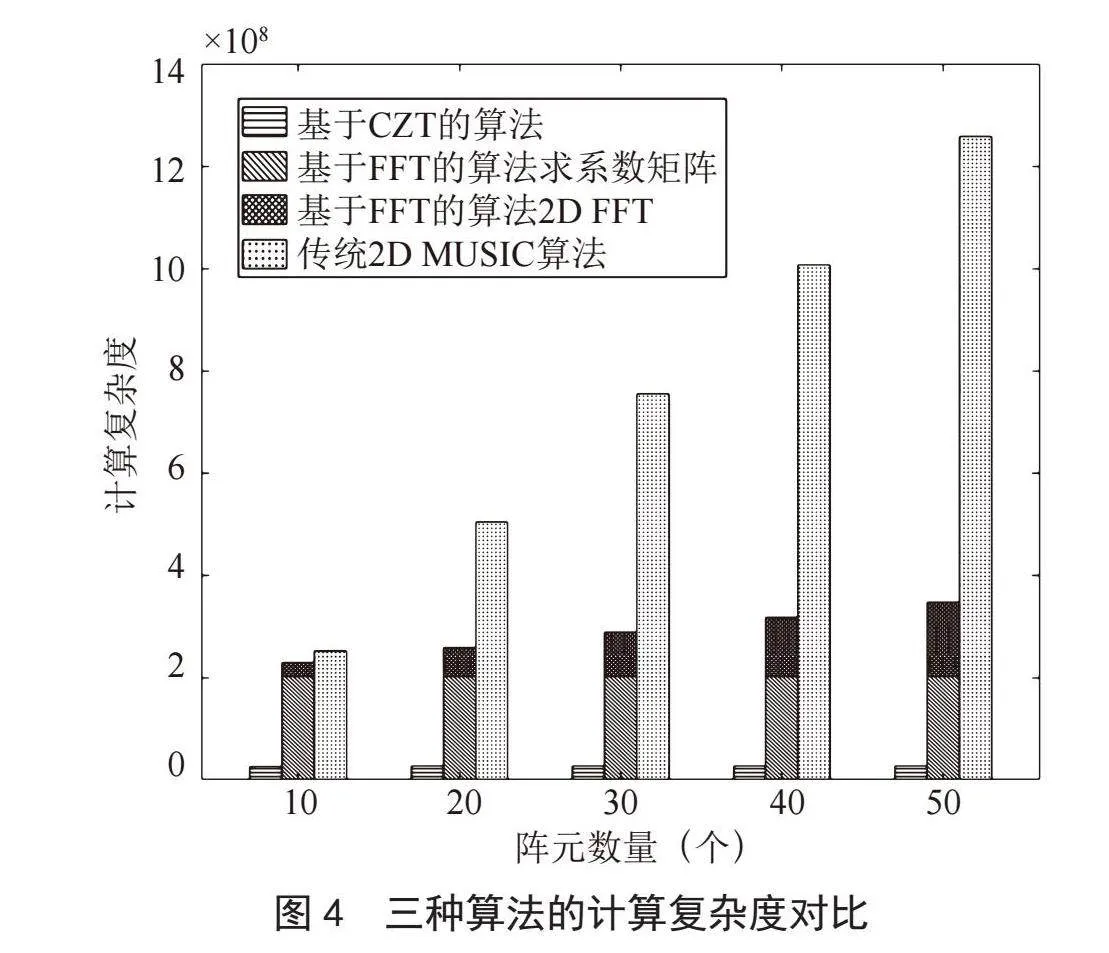
图4给出了三种算法的计算复杂度的对比图,图中基于FFT的算法的复杂度是由系数矩阵和2D FFT两部分的复杂度堆叠累加而成。由表1和图4,可以明显看出,天线数量增加,传统2D MUSIC算法和基于FFT算法的计算复杂度会随着天线数量增加而线性增长,本文提出的算法的计算复杂度受到的影响微乎其微。当阵元数量达到50时,本文提出算法的计算复杂度大约只有传统2D MUSIC算法的2.13%,或只有基于FFT算法的7.72%,可见本文提出的基于CZT的算法的计算复杂度是明显低于传统算法。
3" 仿真结果及分析
3.1" 空间谱仿真结果
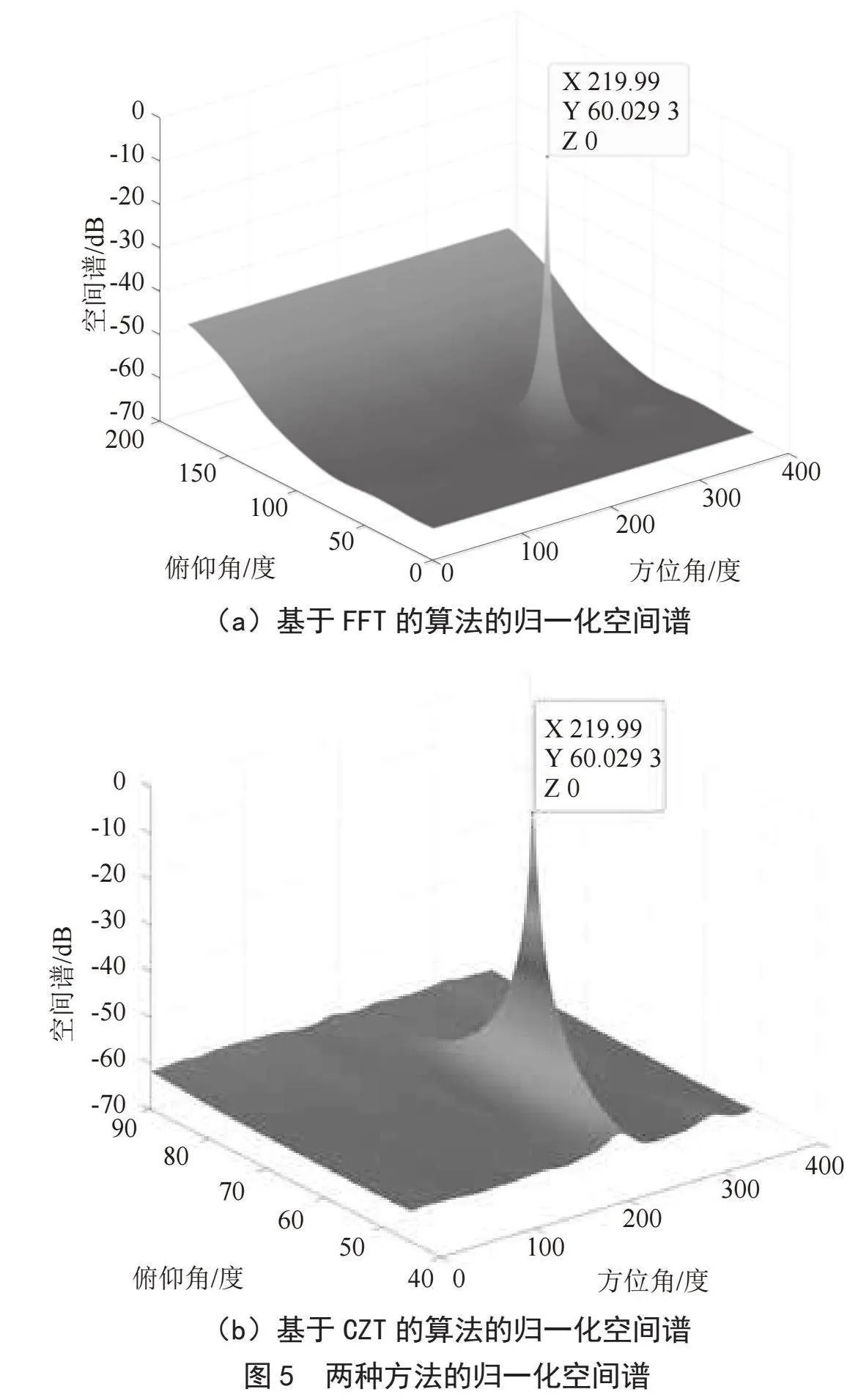
空间谱仿真实验,以计算θ∈[π/4,π/2)和ϕ∈[0,2π)区间的空间谱为例,对本文提出的两种方法与基于FFT的2D MUSIC算法的空间谱结果进行比较。这里选用的是一个32阵元的半球面共形天线,阵列半径R=0.15 m,信源数K=3,快拍数为1 000,信源方位角的俯仰角方向分别为220°、60°,信噪比为20 dB,其他参数的选取与复杂度分析的参数一样。
实验结果的归一化空间谱如图5所示,其中图5只截取了θ∈[0,π/2)范围的空间谱。可以看出提出的算法和基于FFT的算法种方法均能很好地实现DOA估计,在信噪比20 dB的情况下,误差小于为0.1°,两算法分辨率均是360°/4 096≈0.087 9°,所以该空间谱估计结果的误差主要来源于分辨率,算法具体的误差分析还需进行蒙特卡洛仿真比较统计误差来实现。
3.2" 算法误差分析
本文提出的算法、基于FFT的算法、传统MUSIC算法的分辨率均是360°/4 096≈0.087 9°。在算法误差分析中需要在不同阵元数量情况下,对基于CZT的算法、基于FFT的算法以及传统MUSIC算法的DOA估计的结果进行均方根误差(Root Mean Square Error, RMSE)对比。实验使用半球面共形天线,信号快拍数为100,其他参数的设置均与空间谱仿真实验的参数相同,用蒙特卡洛实验模拟次数为500。
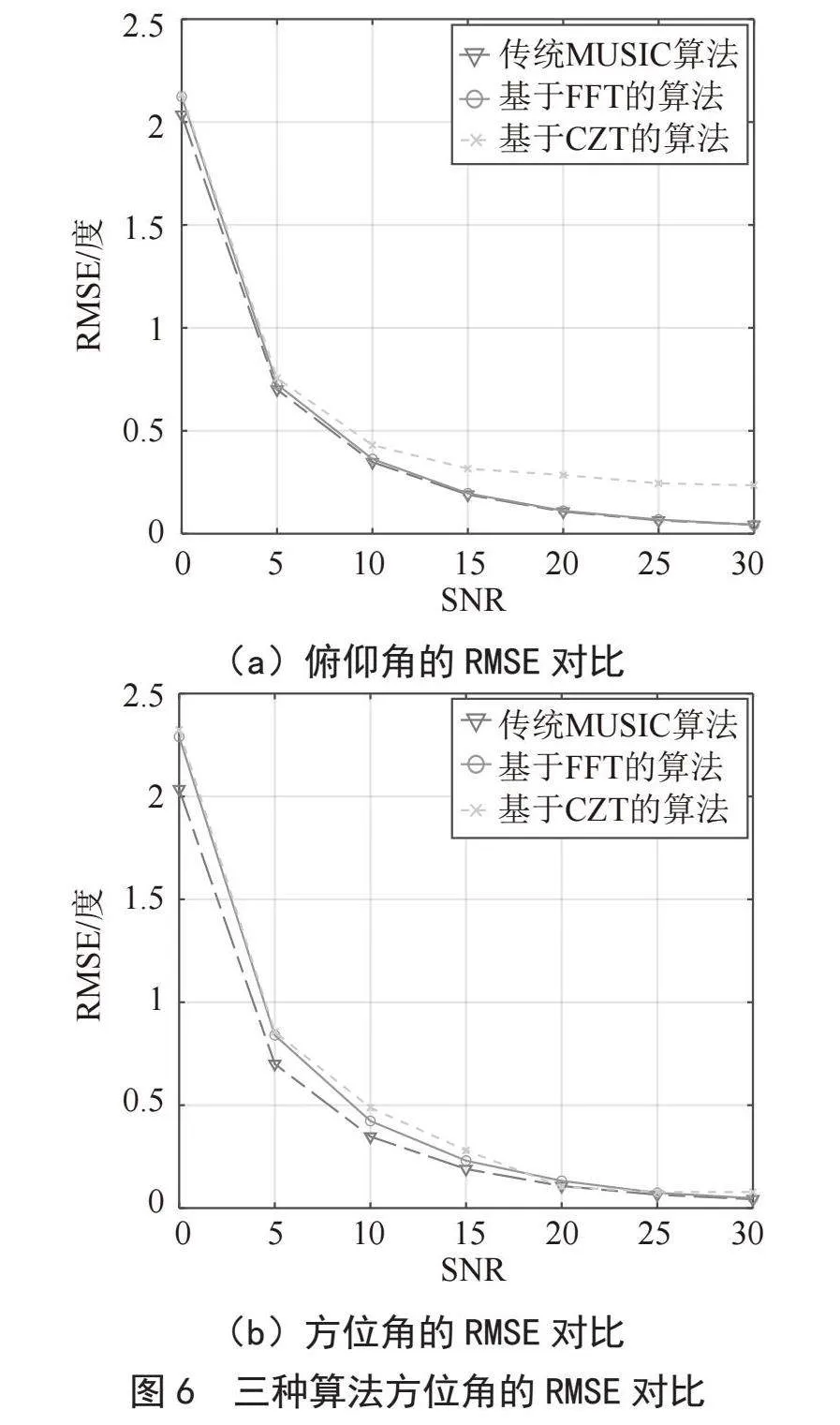
图6对三种算法的俯仰角、方位角的RMSE分别进行绘图对比。在本实验所有SNR范围内,基于FFT的算法在俯仰角和方位角上的RMSE均不超过传统MUSIC算法的6%,两方法的误差结果差距很小,得益于系数矩阵对中心重要元素的正确截取,与预期的结果相吻合。在信噪比低于10 dB时,基于CZT的算法在方位角、俯仰角上的RMSE不超过基于FFT的算法的2%、5%;信噪比在10~20 dB之间时,提出的算法在方位角和俯仰角上的RMSE均不超过0.5°;在信噪比大于20 dB时,提出的算法俯仰角的RMSE不超过0.25°,方位角的RMSE不超过0.2°;在本实验所有SNR范围内,提出的算法的RMSE和基于FFT的算法的RMSE的差距均不超过0.2°。
4" 总" 结
本文提出的两种基于频谱细化的DOA估计方法,不受阵列形状的限制,能够直接应用在任意阵列中。用频谱细化的FFT代替2D FFT,减少了冗余和无用角度范围的计算量,将计算复杂度降低至基于FFT的2D MUSIC算法的数十分之一,算法复杂度几乎不受天线数量的影响,非常适用于大规模阵列,尤其是大规模MIMO系统。这种方法还能在降低复杂度的情况下,保持较高的精准度,以较小的精准度代价换取低复杂度极大的降低,复杂度低但精度略低的方法非常适合对目标初步的快速捕获。如果要将本文提出的方法应用在工程中,要想更好地实现实时计算,还需要对算法进行并行处理的优化,降低运算规模,提高并行度,值得更加深入地研究。
参考文献:
[1] SCHMIDT R,SCHMIDT R O. Multiple Emitter Location and Signal Parameters Estimation [J].IEEE Transactions on Antennas and Propagation(0018-926X),1986,34(3):276-280.
[2] DORON M A,DORON E. Wavefield Modeling and Array Processing.Ⅱ. Algorithms [J].IEEE Transactions on Signal Process(1053-587X),1994,42(10):2560-2570.
[3] ZHUANG J,DUAN C,WANG W,et al. Joint Estimation of Azimuth and Elevation via Manifold Separation for Arbitrary Array Structures [J].IEEE Transactions on Vehicular Technology(0018-9545),2018,67(7):5585-5596.
[4] 彭龙飞.黑障的产生及消除方法 [J].大飞机,2017(3):86.
[5] 喻明浩,邱泽洋.飞行器大气再入过程中黑障缓解方法综述 [J].中国空间科学技术,2022,42(2):1-12.
[6] 邓磊磊.ZFFT和CZT频谱细化方法在频率估计中的应用 [C]//中国声学学会水声学分会2021~2022年学术会议论文集.青岛:[出版者不详],2022:83-86.
[7] DONG L J,XE W L,WANG C F,et al. Enhanced Precision in Frequency and Phase Spectrum in Optical Frequency Domain Reflectometry Using Zoom-FFT Based Spectrum Refinement [C]//2023 IEEE 15th International Conference on Advanced Infocomm Technology (ICAIT).Hefei:IEEE,2023:312-315.
[8] COSTA M,KOIVUNEN V,RICHTER A. Low Complexity Azimuth and Elevation Estimation for Arbitrary Array Configurations [C]//2009 IEEE International Conference on Acoustics, Speech and Signal Processing. Taipei,IEEE,2009:2185-2188.
[9] LANDMANN M,RICHTER A,THOMA R S. DoA Resolution Limits in MIMO Channel Sounding [C]//IEEE Antennas and Propagation Society Symposium,2004.Monterey:IEEE,2004:1708-1711.
[10] DORON M A,DORON E. Wavefield Modeling and Array Processing. Ⅰ. Spatial Sampling [J].IEEE Transactions on Signal Processing: A publication of the IEEE Signal Processing Society,1994,42(10):2549-2559.
[11] HOYER E,STORK R. The Zoom FFT Using Complex Modulation [C]//ICASSP 77. IEEE International Conference on Acoustics, Speech, and Signal Processing.Hartford:IEEE,1977:78-81.
[12] 应启珩,冯一云,窦维蓓.离散时间信号分析和处理 [M].北京:清华大学出版社,2001.
[13] XU G,KAILATH T. Fast Subspace Decomposition [J].IEEE Transactions on Signal Processing: A publication of the IEEE Signal Processing Society,1994,42(3):539-551.
作者简介:姜科良(1999—),男,汉族,山东平度人,硕士在读,研究方向:阵列信号处理;黄治江(1987—),男,汉族,重庆綦江人,副研究员,博士,研究方向:阵列信号处理、无线测控通信技术;解楠(1975—),男,汉族,山东胶东人,研究员,博士,研究方向:测控通信、卫星导航。