





摘" 要:文章以核密度估计方法对格网化的研究区域建立量化单元值,基于探索性空间数据分析(ESDA)建立城市热点聚集模型。首先以最小均方误差探索最优视宽与格网单元划分标准;其次基于“辐射衰减效应”计算格网单元核密度值;最后采用Morans I指数定量分析各类设施点的高值聚集热点,并在二三维下对热点区域进行可视化。与不同视宽下交通类热点探测结果相比,最优视宽不仅满足了交通设施点的连续分布,同时又避免了过渡平滑问题。通过工商企业数据对模型进行实验,证明了该方法能有效提取不同类型设施在城市区域中的分布热点范围。
关键词:城市热点;ESDA;地理空间分析;核密度估计
中图分类号:TP391" " 文献标识码:A" 文章编号:2096-4706(2024)18-0152-06
Establishment of Urban Hotspots Aggregation Model Based on Exploratory
Spatial Analysis Method
XU Yufeng, SUN Xiuqiao
(Beijing North-Star Technology Development Co., Ltd., Beijing" 100120, China)
Abstract: This paper uses the kernel density estimation method to establish the quantified unit values of the grid study area, and establishes the urban hotspot aggregation model based on the Exploratory Spatial Data Analysis (ESDA). First, the Minimum Mean Square Error is used to explore the optimal aspect ratio and the grid cell division standard. Then, the kernel density value of the grid unit is calculated based on the “radiation attenuation effect”. Finally, Morans I index is used to quantitatively analyze the high value aggregation hotspots of various facilities, and hotspot area is visualized in both 2D and 3D. Compared with traffic hotspots with different aspect ratio, the optimal aspect ratio not only satisfies the continuous distribution of traffic facilities, but also avoids the problem of" transition smoothing. Experiments on the model are carried out through the data of industrial and commercial enterprises, which show that the method can effectively extract the hotspot distribution of different types of facilities in urban areas.
Keywords: urban hotspot; ESDA; geospatial analysis; kernel density estimation
0" 引" 言
热点是由具有高值对象的地理要素在局部地理空间内频繁聚集出现形成的区域。城市基础设施空间点数据涵盖了城市各类设施的位置信息与属性信息,在局部地理空间下往往呈现聚集型分布特征,不同类型的城市热点数据在空间布局上存在差异,使得不同职能类型的城市中心在空间分布上也存在差异[1],如商业中心区的金融设施点、文化中心区的教育型设施点等。利用城市空间分析方法研究数据点的地理分布特征与聚集模式,可以为城市发展规划、决策以及商业布局等研究提供重要的信息服务[2]。
在热点分析领域,相关研究主要是通过融合空间密度估计、空间自相关技术和等值线方法来界定空间点数据热点的范围[3]。在传统城市和区域分析中,通过对密度计算结果简单直观地获取点群的聚集或离散等分布特征。然而该分析过程中缺少量化统计评价的干涉,即“密度值高于多少是真正意义上的热点”问题的回答[4]。胡庆武等[5]利用用户位置签到数据,采用均匀划分的网格和ESDA(Exploratory Data Spatial Analysis)方法进行热点探测与商圈挖掘;周勍等[6]以出租车上下车点数据格网化探测城市热点与非热点区域。这类方法在均匀划分格网的标准上是通过比较或者经验来划分格网单元大小,而格网大小的选取直接影响热点区域的界定,因而在理论上不具有说服力。近年来,基于时空数据进行城市热点区域挖掘是研究的热点,大多数是采用聚类算法来发现城市热点区域,如王田雨等[7]提出的改进谱聚类算法,王浩成等[8]提出的分布式多阶段网格聚类算法等都进一步为城市热点区域研究提供了有力的基础。
1" 研究区域与数据
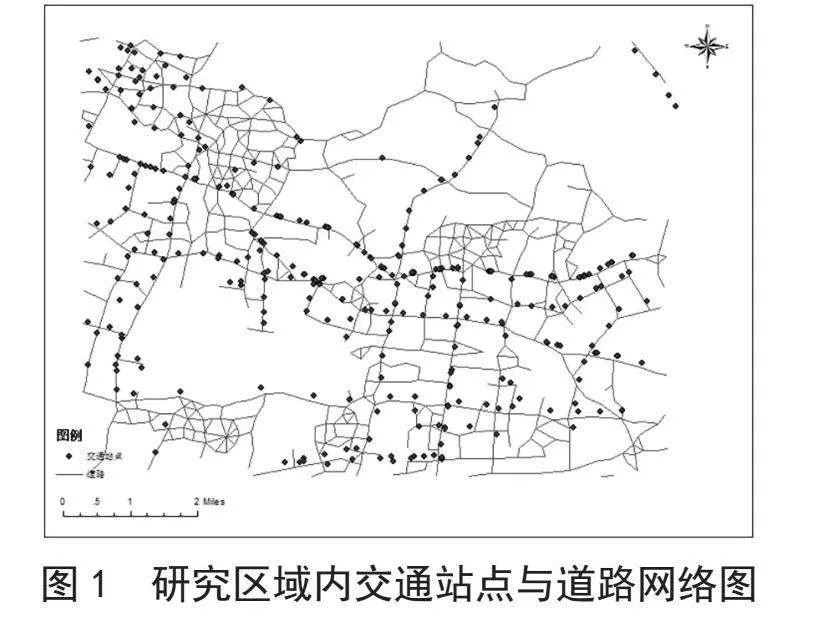
本文以武汉市洪山区光谷广场为中心,西南延伸至野芷湖,东北延伸至严西湖东的矩形区域作为测定热点的研究区域。本文选用交通站点数据和工商企业数据作为数据源研究城市热点聚集模式。全部数据来源于百度地图开放平台。交通点数据包括所在地址信息、点位置信息、站点名称、站点类型和站点经由公交信息在内的12项属性,删除站点位置缺失记录条目以及合并站点信息相同记录条目后,共有322条有效交通站点记录,如图1所示。
2" 研究方法
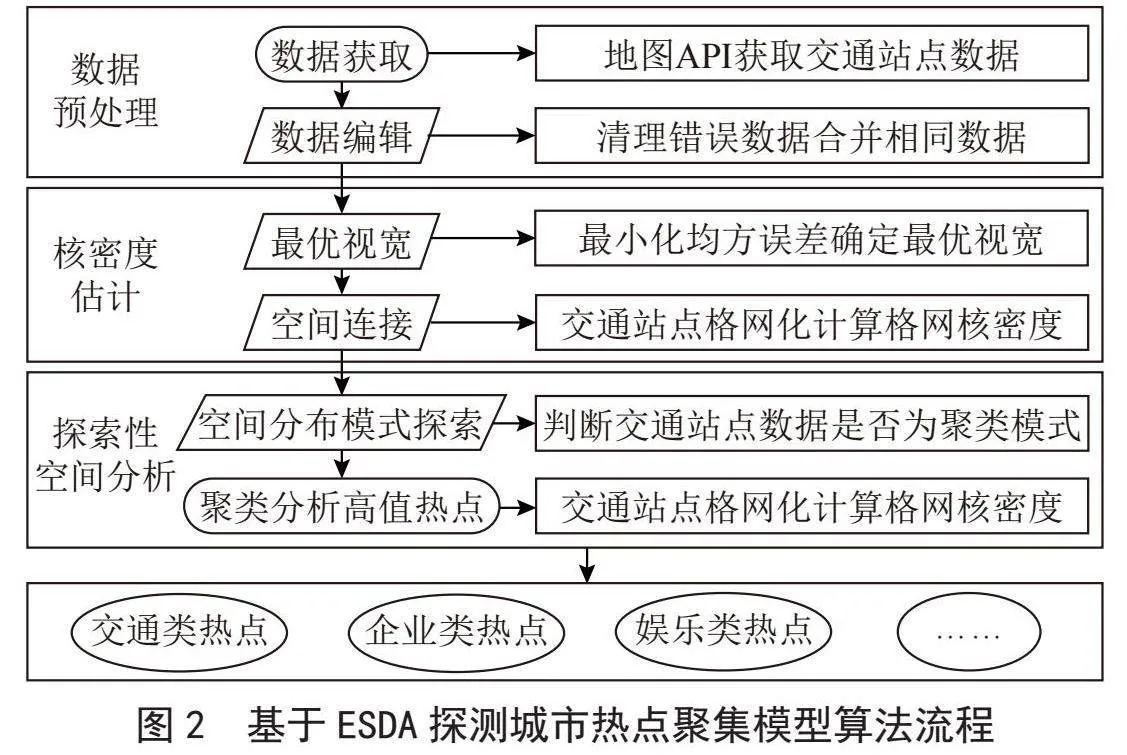
本文将核密度估计理论和探索性空间数据分析(ESDA)应用于城市热点聚集模型研究。POI点数据(包含位置与属性数据)为大量离散要素点,在空间上不具有明显的连续性和邻接性,不利于探索性空间数据分析方法度量其空间分布模式。因而构建固定像元大小的格网并对其进行空间连接,将存在空间包含关系的点状数据映射到对应的格网中。其次运用利用核密度估计方法计算得到格网单元密度值,采用全局莫兰指数(Global Morans I)统计方法来度量研究区域内格网核密度值的空间分布模式,利用局部莫兰指数(Local Morans I)探索具有统计显著性的高值聚类热点、冷点和空间异常值位置。最后实现探测结果的可视化需求。具体流程如图2所示。
2.1" 核密度估计
核密度(Kernel Density Estimation)是计算每个输出栅格像元周围的POI点要素的密度[9]。以点S为圆点、h为搜索半径的圆内样本点对点S的累计贡献值,即为点S处的密度值,而其中的核函数可以理解为点事件i距离点S的权重,点i离点S越远,对于点S处的密度值贡献越小。核函数k考虑了距离衰减效应,即距离中心越近的样本点分配的权重越大。而点S处的核密度值即是圆内所有样本点密度函数之和。设事件点S处的核密度值为f(S),如式(1)所示:
(1)
其中,f(S)为点S处的核密度值;h为搜索半径(或视宽);k为核函数;dis为点事件i距离核中心的欧式距离;n为核中心S在其视宽内样本点数量;ci为点事件i自身系数权重。
2.2" 最优视宽确定
由式(1)可知,核密度曲线形式最终取决于3个重要的参数:核函数、视宽与自身系数权重的选择。核函数的选择主要考量其权重赋值,相比于视宽的选择,不同核函数的形式对于核密度估计的影响较小,本文研究选用高斯核函数。
视宽h的选取极大地影响到核密度估计曲线的光滑程度,以及最终展现每个数据包含细节信息的程度[10]。如果r取较大的值,此时核密度曲线的图像应该是较为光滑的曲线,但同时是以损失数据包含的一些细节信息为代价;反之核密度曲线图像是不光滑的折线,但它能反映出每个数据所包含的细节信息。以最小化“均方误差”(MSE)作为衡量标准,当均方误差最小时的视宽则为最优视宽,其计算式为:
(2)
式(2)通过最小化积分均方误差可以得到最优视宽h,其中AMISE是渐进均方误差,AMISE的最小值即下微分方程等式的解,K为Gaussian核函数,得到最优视宽:
(3)
式中由样本标准差s来替代,n为样本点个数。根据交通站点数据样本可知,n=332,o由样本标准差S替代,S=3 012,带入可得hopt≈1 000 m。
自身权重系数c值主要包括经由车次数和车次类型两方面,如果站点A经由的公交车次有16趟,站点B经由的地铁车次有2趟,以承载客流量为标准,一趟地铁载客量约1 500,公交载客量约为50人,则站点A与站点B的权重指数ca:cb=4:15。因此,指标权重系数的计算式为:
(4)
式(4)中:B为公交车次数;H为地铁车次数。
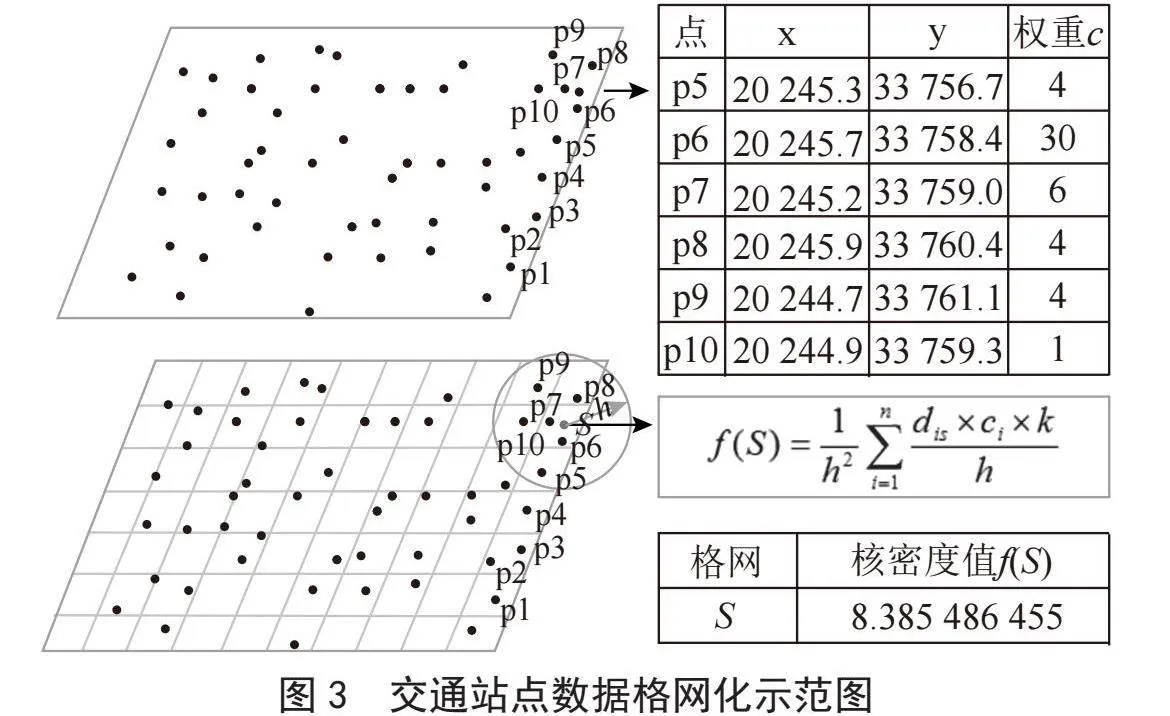
2.3" 空间格网化
以研究区域为范围,构建固定像元大小的格网,将研究区域抽象成由点状要素和线状要素组成的线性网络系统,将存在空间包含关系的交通站点数据映射到对应的格网中去[11-12],如图3所示。划分后的格网宽度一般为视宽的1/10,即将研究区域格网化为12 423个100 m×100 m大小格网单元,依据式(1)得出所有格网中心点的核密度值,作为该格网的密度值。
2.4" 空间自相关检验与分析
通过对空间自相关的测度可以检验具有空间位置的某要素的观测值是否显著地与其相邻空间点上的观测值相关联[13]。本文引入Global Morans I和 Local Morans I来测度全局和局部的空间关联特征。前者是用于度量整个研究区域的空间关联与空间差异程度的指标,评估某一属性在整个研究区域内为聚类模式、离散模式或随机模式;后者是用于分析局部地区之间是否存在相似或相异的属性值聚集在一起的指标,即测度相邻地区之间属性值的异质性[14-15]。
2.4.1" 全局空间自相关评估分布模式
基于研究区域内格网的核密度值分布值,Global Morans I的计算式为[16]:
(5)
式(5)中,N为观测值数目;Xi、Xj为区域i与j的观测值;X为整个研究区域内观测值的均值;W为空间权重矩阵,Wij为空间单元i和j的空间连接关系,基于共享边界与定点为前提,与目标元素具有邻接关系的元素值为1,否则为0。Morans I取值介于-1~1之间,在给定的显著性水平下,若Morans I>0,则表示该属性数据在空间上存在集聚效应;当Morans I指数趋向于0时,表明观测值之间不存在空间自相关,呈现出随机模式;当Morans I<0,则表明该属性数据在整体空间上呈现出分散模式[15]。
(6)
可通过式(6)计算Z得分来检验交通站点核密度值是否具有统计学上的显著性。空间自相关的零假设表明,所分析的属性在研究区域内的要素之间是随机分布的。计算交通站点核密度数据的全局自相关结果,其零假设概率p值为0,Z得分值为156.10,远大于99%置信度情况下2.58的临界值,拒绝零假设,随机产生此聚类模式的可能性小于1%,Morans I=0.994 5,说明交通站点核密度值数据符合典型聚类模式统计特征,可进行交通类热点探测分析。
2.4.2" 局部空间自相关提取高值聚类热点
基于研究区域内格网的核密度值分布值,使用Local Morans I统计量来识别具有统计显著性的热点、冷点和空间异常值。计算式为:
(7)
式(7)中,各参数与式(6)中全局指标Global Morans I参数含义相同,通过计算得到每个格网的Local Morans I指数。仍然通过式(6)计算Z得分来检验交通站点核密度值是否具有统计学上的显著性,根据Local Morans I指数、Z得分和p值进行分类标识,如表1所示。
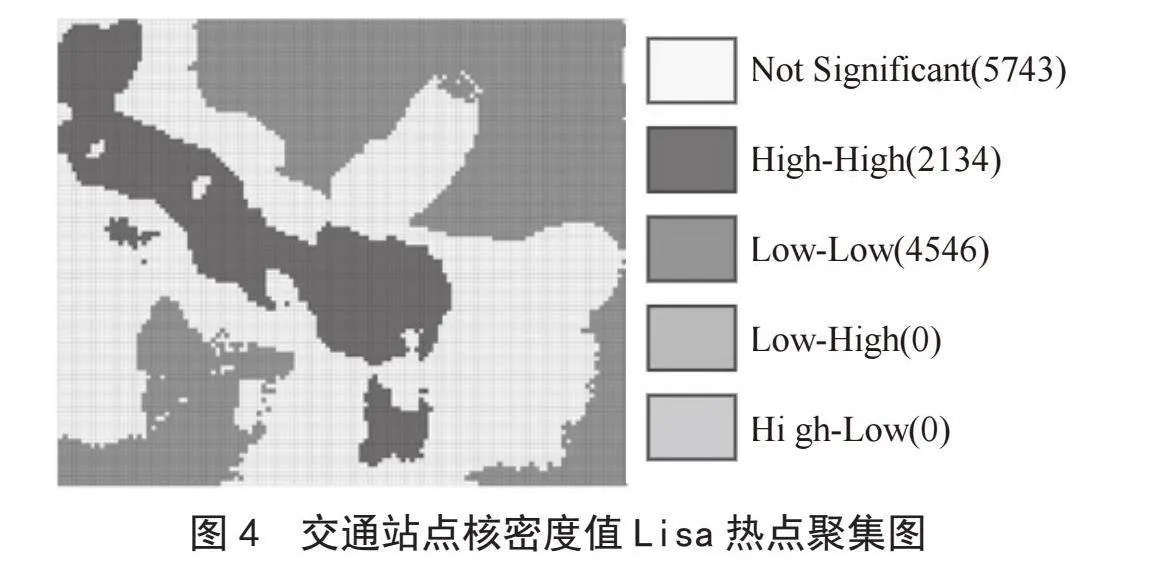
基于研究区域12 423个格网空间单元,得到具有高值聚类特征的空间单元2 146个。按照局部空间自相关指标生成的Lisa聚集图结果如图4所示,红色代表高高聚集(2134),表明其空间单元和其周边空间单元的核密度值都较高,同时也是本研究中认为对应的城市交通类热点区域所在,在整个研究区域中面积占比17%;灰色代表低低聚集(4546),表明其空间单元和其周边空间单元的核密度值都较低,这部分空间单元即核密度值低的聚集区,本研究中认为属于非城市交通类热点区域,该区域在整个研究区域中占比36.5%;灰蓝和粉色分别代表低高聚集和高低聚集,表明其空间单元和其周边空间单元的核密度值存在一定的竞争关系,从图4上看来,这两部分的空间单元个数为0,说明由交通站点空间连接形成的核密度数据不存在这种高—低的竞争关系;而无色则为不显著,造成这种分布的原因主要是其空间单元的核密度值层次不一,没有明显的空间相关性。
2.5" 不同视宽交通热点探测结果
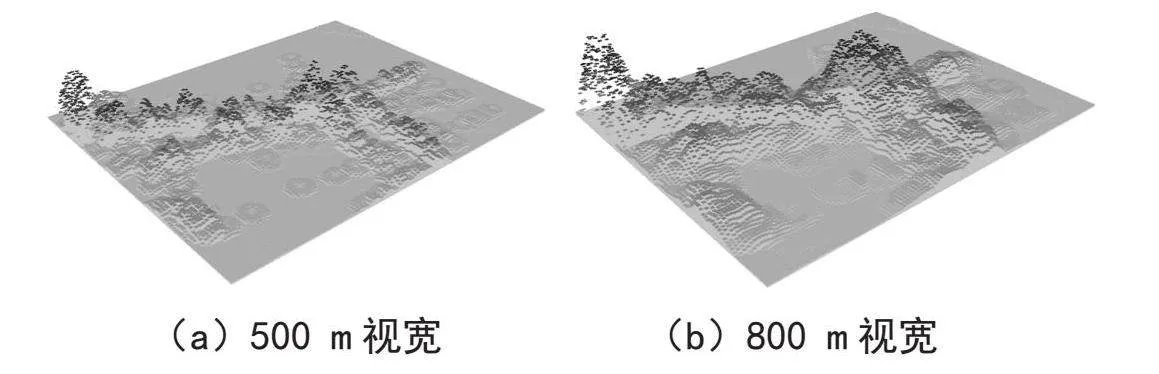
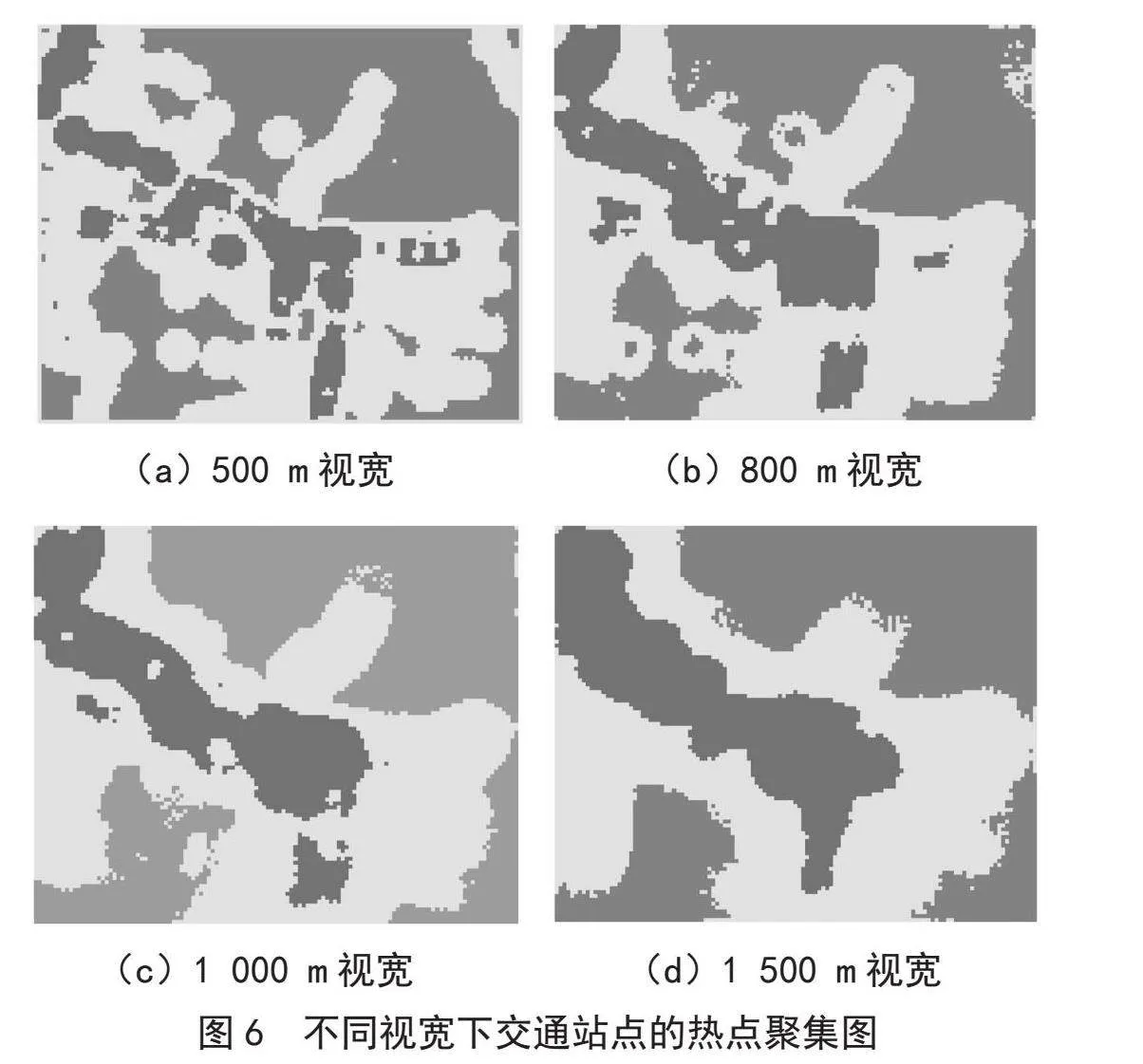
以研究区域为范围,构建100 m×100 m大小的格网时,分别生成视宽为500 m,800 m,1 000 m以及1 500 m的格网。如图5(a)中当h取500 m时,计算结果产生了很多的局部极大值,甚至于一个数据点就可以产生一个局部山峰;当h取1 500 m时,计算获得的核密度值仅有两个局部极大值,波谷变化几乎不明显,整个研究区域虽然连续分布,但过渡平滑,形成了波峰带。当核密度取800 m和1 000 m时,核密度值波峰波谷变化明显,符合热点聚集的性质,特别是在最优视宽1 000 m时,核密度高值点与低值点区分明显,形成了很强的视觉冷热效果。从图6不同视宽下产生的城市热点区域可以看出,当h较小时产生了很多的局部聚集区;当h很大时,整个研究区域将只有一个聚类中心。以上这两种情况获得的结果均不符合聚类宗旨。因此在生成格网核密度表面时,选择带宽的大小很重要,不能过大也不能过小。本文在计算研究区域密度时选用最优带宽h=1 000 m进行核心估计。
3" 结果与分析
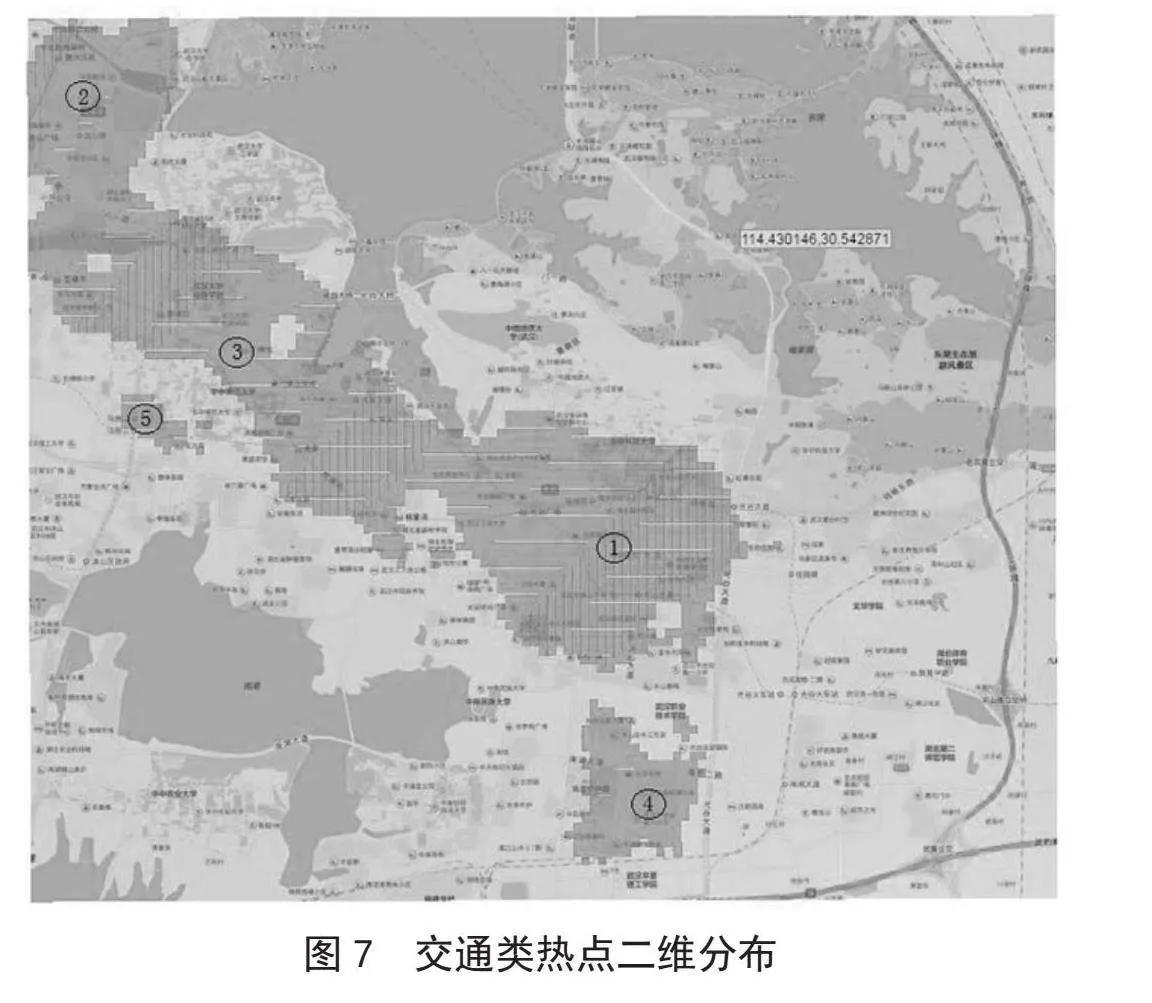
利用局部空间自相关聚类探测的交通站点高值热点(图4的Lisa热点聚集图)作为交通类热点区域,以Local Morans I指数值作为热值强度,将热点区域结合研究区域矩形条拉伸,得到交通类热点的三维立体可视化地图,结果如图7、图8所示。
可以归纳为有5块不规则区域构成了研究区域交通类热点分布,根据聚集程度先后有:
1)区域编号为1的一个广阔区域,位于光谷广场为中心的核心区域并向南、北、东、西4个方向均匀扩散形成的区域。Morans I指数在这个区域达到最高,在该区域的地理中心偏南位置,占了整个热点区域面积的34.5%,该区域内包括59个公交站点,1个地铁站点,对于原始332条数据占比18%,是发展成熟的热点聚集区域。
2)区域2位于研究区域西北角,对应地图上中南商圈地理方位,沿东北-西南方位发展的趋势。该区域的Morans I指数达到次高,热点区域面积也仅次于区域1,囊括有洪山广场与楚河汉街两个地铁站点,占整个热点区域面积的13%,是发展较为成熟的热点聚集区域。
3)带状区域3沿珞瑜路经广埠屯、街道口、宝通寺的区域。该区域Morans I指数有4次起伏,连接起区域1和区域2,包括有70个公交站点,5个地铁站点,占整个热点区域面积的40%,是发展次成熟的热点聚集区域。
4)区域4位于中南部,该区域对应光谷软件的地理方位,东临关谷大道,北侧武汉职业技术学院,共有17个公交站点分布,Morans I指数偏低,同时区域占比面积也较小。
5)小块区域5位于雄楚大道与珞狮路交界北侧,该区域是以公交站点聚集而来的交通类热点。
4" 结" 论
城市交通站点与企业点数据作为一种空间点数据,记录城市交通状况、企业分布状况,利用空间数据挖掘理论与方法研究城市各类设施的地理分布特征与聚集模式。本文以武汉市研究区域内交通站点数据为数据源,系统地研究了基于ESDA方法建立的城市热点聚集模型,将核密度估计方法运用于城市热点探测,增加了空间点数据自身权重系数,并以最小均方误差得到的最佳视宽(辐射半径)来计算格网大小,考虑原始空间点数据的离散程度,而不是凭借经验值选择格网大小尺寸。并选用企业点数据验证热点聚集模型,探索得到城市企业类热点。通过将热点结果与研究区域矢量地图进行叠加,得到了不规则大小的热点区域。该结果对城市发展规划、交通部署以及企业布局具有重要的现实意义和应用价值。
参考文献:
[1] 李胜男,刘亚静.基于多源数据的城市职能中心与空间结构识别 [J].地理空间信息,2023,21(6):89-92.
[2] COBURN T C. Statistical Methods for Spatial Data Analysis [J].Urisa Journal,2006,38(4):511-513.
[3] 禹文豪,艾廷华,刘鹏程,等.设施POI分布热点分析的网络核密度估计方法 [J].测绘学报,2015,44(12):1378-1383+1400.
[4] 禹文豪,艾廷华,杨敏,等.利用核密度与空间自相关进行城市设施兴趣点分布热点探测 [J].武汉大学学报:信息科学版,2016,41(2):221-227.
[5] 胡庆武,王明,李清泉.利用位置签到数据探索城市热点与商圈 [J].测绘学报,2014,43(3):314-321.
[6] 周勍,秦昆,陈一祥,等.基于数据场的出租车轨迹热点区域探测方法 [J].地理与地理信息科学,2016,32(6):51-56+127.
[7] 王田雨,吉立新,李邵梅,等.基于改进谱聚类的城市热点区域挖掘 [J].信息工程大学学报,2022,23(3):313-319.
[8] 王浩成,向隆刚,关雪峰,等.基于出租车上下客数据流与分布式多阶段网格聚类的城市热点区域实时探测方法 [J].地球信息科学学报,2023,25(7):1514-1530.
[9] 吴启倩,钱乐祥,吴志峰.基于多源数据的特大城市空间结构识别及空间形态研究 [J].地理信息世界,2020,27(5):32-38.
[10] SÁNCHEZ-SELLERO C,GONZÁLEZ-MANTEIGA W,CAO R. Bandwidth Selection in Density Estimation with Truncated and Censored Data [J].Annals of the Institute of Statistical Mathematics,1999,51(1):51-70.
[11] 吕安民,李成名,林宗坚,等.人口密度的空间连续分布模型 [J].测绘学报,2003(4):344-348.
[12] 吕安民,李成名,林宗坚,等.一种人口连续分布模型的研究 [J].测绘学院学报,2002(1):76-78.
[13] MICHAEL F.GOODCHILD. A Spatial Analytical Perspective on Geographical Information Systems [J].International Journal of Geographical Information Science,1987,1(4):327-334.
[14] 冯永玖,陈新军,杨铭霞,等.基于ESDA的西北太平洋柔鱼资源空间热点区域及其变动研究 [J].生态学报,2014,34(7):1841-1850.
[15] DALLERBA S,CHEN S L. Exploratory Spatial Data Analysis [J].International Encyclopedia of Human Geography,2020:357-365.
[16] 刘虹,薛东前,马蓓蓓.基于ESDA分析的关中城市群县域经济空间分异研究 [J].干旱区资源与环境,2012,26(4):55-60.
作者简介:许玉凤(1994—),女,汉族,河南周口人,中级工程师,硕士,主要研究方向:地理信息系统、空间信息应用;通信作者:孙秀巧(1990—),女,汉族,河北沧州人,中级工程师,硕士,主要研究方向:地理信息系统、空间信息应用。