
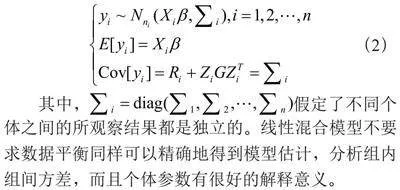

摘" 要:通过对帕金森病语音信号多重共线性纵向高维数据的预处理和分析,可为相关医疗机构提供重要信息。首先采用随机森林对数据进行预处理,得到降维数据集,通过相关性分析得知该数据存在多重共线问题;然后在BP神经网络中引入L2正则化改变其目标函数,解决临床数据经常存在的数据多重共线性,以便更好地拟合线性混合效应模型;最后对比分析引入BP-L2混合算法前后线性混合效应模型的AIC、BIC和-LogLik指标,证明引入该算法的优势。
关键词:帕金森病;随机森林;L2正则化;BP神经网络;线性混合效应模型
中图分类号:TP391" 文献标识码:A" 文章编号:2096-4706(2024)19-0158-06
Application of Linear Mixed Effects Model Based on BP-L2 Hybrid Algorithm in Speech Signals of Parkinsons Disease
LUO Chengmin1,2, WANG Tao1,2
(1.School of Mathematics, Yunnan Normal University, Kunming" 650500, China; 2.Yunnan Key Laboratory of Modern Analytical Mathematics and Applications, Kunming" 650500, China)
Abstract: By preprocessing and analyzing longitudinal high-dimensional data of multicollinearity in Parkinsons disease speech signals, important information can be provided for relevant medical institutions. Firstly, the data is preprocessed using Random Forest to obtain a reduced dimensional dataset. Through correlation analysis, it is found that the data has multicollinearity issues. Then, L2 regularization is introduced into the BP Neural Networks to change its objective function, solving the problem of data multicollinearity in clinical data, so as to better fit the linear mixed effects model. Finally, a comparative analysis is conducted on the AIC, BIC, and -LogLik indicators of the linear mixed effects model before and after the introduction of the BP-L2 hybrid algorithm, demonstrating the advantages of introducing this algorithm.
Keywords: Parkinsons disease; Random Forest; L2 regularization; BP Neural Networks; linear mixed effects model
0" 引" 言
帕金森病(Parkinsons Disease, PD)[1-5]是一种常见的神经退行性疾病,具有复杂的病理生理学,影响了全球超过600万人。PD的确诊方式主要为医生的临床确诊,但目前医护人员紧缺,医疗资源相对不足,而且该病理尚且不明。为了提升医护人员的工作效率,减少患者确诊时间,探索PD病理,在尽可能早的阶段检测PD,能大大提高效率。研究表明,大约90%以上的PD患者在疾病的早期阶段表现出某种形式的声音障碍,相比运动障碍、认知障碍、基因检测、核磁共振和CT等检测手段来说,收集受试者语音障碍纵向数据更具可行性和普遍性,但随着社会的发展,各种医疗设备在不断改进,患者被观察到的各种指标也在增加,并且收集到的纵向数据表现出多重共线性问题——解释变量之间由于存在精确相关关系或高度相关关系而使模型估计失真或难以估计准确,导致原有分析方法效果不佳,这就使得研究者们加快了针对多重共线数据建模的脚步。
针对纵向数据的建模问题,近期很多研究者借助线性混合效应模型来建模,线性混合模型也常被用于纵向的临床数据研究中。臧一腾等人[6]基于中国营养健康调查数据,使用线性混合模型树探究江苏省成年人体质指数纵向变化轨迹及分类,研究结果表明,线性混合模型树可以识别体质指数的变化轨迹,拓展了纵向数据动态变化的研究方法。但是发现纵向数据中常含多重共线性问题,为解决数据多重共线问题,许多学者采取对传统模型进行惩罚、引入机器学习等方法。L2正则化(Ridge regression,Tikhonov regularization),该方法实质上是一种经过改良的最小二乘估计方法。吴喜之等人[7]在著作第二章第7节中,详细阐述了L2惩罚方法的理论结构,并把该方法应用到糖尿病多重共线数据分析中,与lasso方法对比分析,结果表明与L1正则化不同在于,L2正则化函数是可导,可以通过对函数梯度的求解分析直接计算最优解。随着机器学习的迅速崛起,为解决复杂的数据,许多研究者提出了混合算法。Panokin等人[8]给出了一种基于L1联合神经网络的复数据表示方法的研究结果,该方法是对类神经网络在多重共线数据情况下的扩展改进,分析了激活函数的选择对方法性能的影响,数值模拟结果证明了该方法在复杂数据稀疏表示情况下的有效性。于秀君[9]在心脏病临床数据分析中提出了稀疏主成分分析和BP神经网络混合算法——SPCA-BP混合算法,并把SPCA-BP混合算法应用到Logistic模型,与原始模型作对比,引用了该混合算法的Logistic模型预测精度优于原始模型;田子文[10]在解决污水处理问题时,搭建了基于活性污泥1号仿真平台,基于L2正则化和径向基神经网络混合算法,构建了Q-RBF网络,有效提高了模型控制精度和干扰性能。
综上所述,针对具有多重共线性的纵向数据分析,我们尝试性地提出把带有L2正则化惩罚项的BP神经网络混合算法引入到线性混合效应模型中,以此来提高模型的兼容性和精度,并与传统线性混合模型建模结果做比较,阐述在医学数据领域中引用带有BP-L2混合算法的线性混合效应模型的优势,以供医学、统计相关领域分析人员参考。
1" 线性混合效应模型
线性混合效应模型[11](Linear Mixed Effects Model, LME)是Laird和Ware提出的,其一般形式为:
(1)
其中,yi表示响应变量,Xij表示固定效应β的协变量矩阵,Zij表示随机效应αi的协变量矩阵,ei表示随机误差向量,表示第i个个体的ni次测量误差,各个分量之间是相关的。β表示p*1维固定效应,αi表示个体随机效应。一般而言,Zij的列表示Xij的子集,服从多元正态分布:
(2)
其中,假定了不同个体之间的所观察结果都是独立的。线性混合模型不要求数据平衡同样可以精确地得到模型估计,分析组内组间方差,而且个体参数有很好的解释意义。
2" BP-L2混合算法
2.1" L2正则化
L2正则化[10]是一种最为常用的正则化手段,又称为权重衰减。与L1正则化不同在于,L2正则化函数是可导,可以通过对函数梯度的求解分析直接计算最优解。对于BP神经网络本身来说,它具有一定的鲁棒性,所以在每个时刻都允许有很小的误差,这对于L2正则化的应用来说非常合适。其表现形式为:
(3)
其中,λ为二范数的正则化参数,如果λ过大,会导致模型欠拟合。反之,若λ过小,模型可能过拟合;ω是被惩罚参数的二范数。
2.2" 混合算法
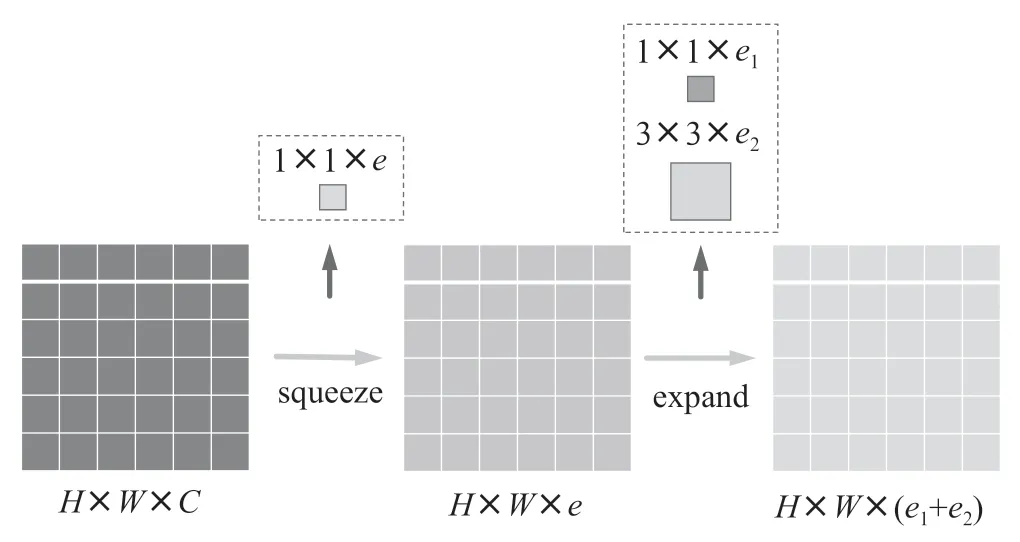
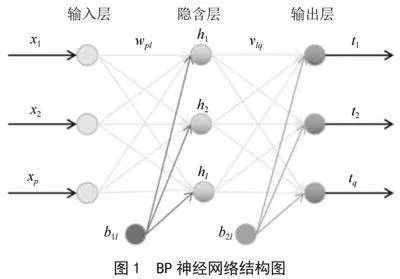
针对本文需解决的数据多重共线问题与L1和L2积分求解式的难易程度问题,选用L2正则化改变BP神经网络的目标函数,组成BP- L2混合算法,BP神经网络结果图如图1所示。
1)对原始数据进行标准化处理。
2)按照合理比例划分原始数据。
3)构建BP神经网络。确定输入层神经元个数,隐含层神经元个数,输出层个数1,设定训练次数为10 000次,根据需要设定训练目标,学习速率为0.001。
4)BP神经网络参数设置。随机在区间[-1,1]中取值,赋予网络权重w、v,阈值b11、b21作为初始值。
5)随机选取一组样本X(k)作为BP神经网络的输入值:
(4)
6)计算隐含层输入值G(k)和输出值H(k):
(5)
(6)
7)计算输出层输入值U(k)和输出值T(k):
(7)
(8)
8)计算目标函数,即均方误差E(k):
(9)
9)梯度下降法更新并计算从隐含层到输出层的权值矩阵V和输出层各神经元阈值b1i:
(10)
(11)
10)梯度下降法更新并计算从输出层到隐含层的权值矩阵W和输出层各神经元阈值b2j:
(12)
(13)
11)随机选取另一组样本提供给BP神经网络继续训练,返回3),直至m组数据训练完毕。
12)根据事先设定好的训练目标,判断训练误差是否满足要求。若满足,终止训练;否则继续。
13)更新网络的迭代次数,返回3)。
14)利用训练好的BP神经网络,对训练集和测试集进行预测。
15)重复1)至13),最终构建出网络:
(14)
在其他学者所研究的混合算法的启发下,本文提出BP-L2混合算法,在帕金森病语音信号数据的预测模型上有所创新。在BP神经网络中通过引入L2正则化方法,在最大程度保留原始数据信息的基础上,解决临床数据经常存在的数据多重共线问题。而且基于此方法训练出来的模型亦具有处理非线性数据的能力,更贴合实际数据需求。
3" 实证分析
3.1" 数据描述
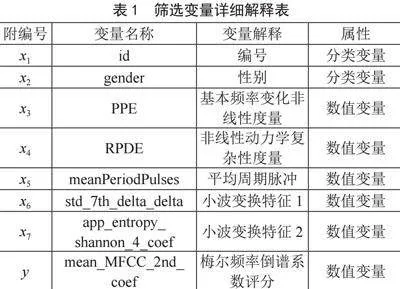
使用的数据来自UCI机器学习存储库[12-13],该数据由188名PD患者和64名健康者组成,其中PD患者由107名男性和81名女性组成,年龄在33至87岁(65.1±10.9)之间;健康个体由23名男性和41名女性组成,年龄在41至82岁之间(61.1±8.9)。经各种语音信号处理算法得到8个一级指标和754个二级指标变量,其中梅尔频率倒谱系数评分经常在临床分析中被看作是响应变量。
3.2" 建立模型并分析
3.2.1" 数据预处理
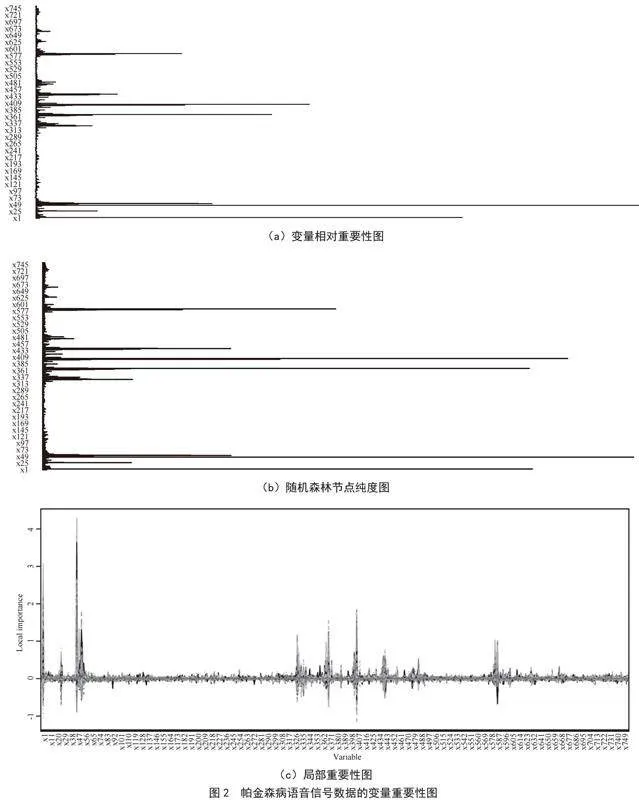
1)随机森林降维。由于本文数据为生物统计学中的高维数据,采用随机森林进行降维,结果如图2所示。
通过随机森林预处理,根据在总体中重要的变量在局部中也重要的原则,针对7个模块的帕金森病语音信号数据进行变量重要性和局部变量重要性作对比。分析图2得知:基线特征和小波变换特征在总体上对帕金森病有着特殊的意义,值得帕金森病研究人员和医疗机构重视。筛选结果如表1所示。
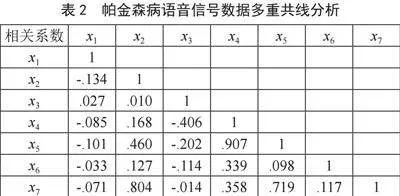
2)多重共线性分析。计算各自变量之间的相关系数,根据自变量之间的相关系数值很大(接近于1或-1)的原则,来判断可能存在共线性的变量。结果如表2所示:变量x2与x7、x4与x5、x5与x7的相关系数很高,接近于1,可能存在共线性。
3.2.2" 建立线性混合效应模型
根据上述变量筛选和分析,针对带有多重共线性的帕金森病语音信号数据进行建模分析:
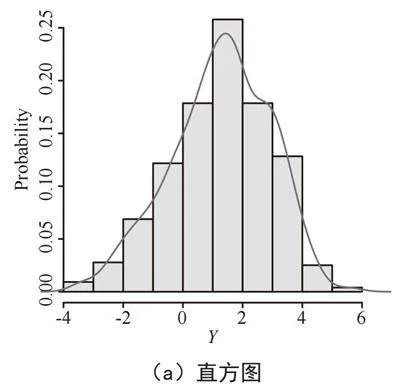
1)正态性检验。结合上述分析,在帕金森病语音信号数据分析构建线性混合效应模型之前,我们需要对响应变量做正态性检验,判断其是否服从正态分布。
观察图3得知:图3(a)直方图和图3(b)QQ图中响应变量y——梅尔频率倒谱系数近似服从正态分布。
2)模型的建立与求解。结合前述分析,构建线性混合效应模型(LME):
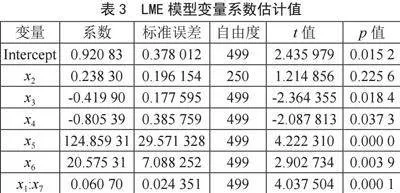
步骤一:通过计算获得LME模型各变量系数估计值,如表3所示。
其中变量x5和x6平均每变化单位1,响应变量梅尔频率倒谱系数评分就会相应增加约124.86和20.58,对梅尔频率倒谱系数评分影响甚大;x3和x4虽对梅尔频率倒谱系数评分影响绝对值不大,但其每变化单位1,梅尔频率倒谱系数评分就会减少约0.42和0.81,造成负影响。
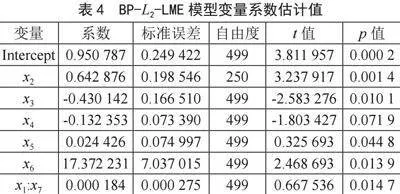
步骤二:通过计算引入BP-L2混合算法的线性混合效应模型获得各变量系数估计值,如表4所示。
其中变量x6平均每变化单位1,梅尔频率倒谱系数评分就会相应增加约17.37,对梅尔频率倒谱系数评分影响较大;x3和x4依然对梅尔频率倒谱系数评分造成负影响,其每变化单位1,梅尔频率倒谱系数评分就会减少约0.43和0.13。
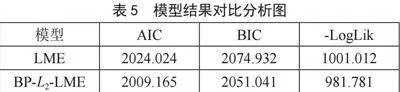
步骤三:根据如下标准来判断、对比分析两个模型:AIC赤池信息准则(AIC值越小,表示模型性能越好);BIC贝叶斯信息准则(BIC值越小,表示模型性能越好);-LogLik对数似然值(绝对值越小说明模型拟合越好),结果如表5所示。
分析表5发现:引入BP- L2混合算法后使得LME模型更有效,能更好地解释纵向数据的变化轨迹,改善数据多重共线性的问题。
4" 结" 论
本文首先从UCI机器学习存储库获取帕金森病语音信号纵向数据,通过去除异常值、随机森林可视化展示等预处理,发现帕金森病语音信号数据存在多重共线性。为解决纵向数据多重共线问题,我们尝试性地提出把带有L2正则化惩罚项的BP神经网络混合算法引入到线性混合效应模型中,以此来提高模型的兼容性和精度,并与传统线性混合模型建模结果做比较,研究数据表明:引入了BP- L2混合算法后的线性混合模型指标AIC、BIC和-LogLik值均小于传统x线性混合效应模型的指标。故本文所提出的BP- L2混合算法能够有效兼容数据多重共线性更好地拟合模型,提高了联合模型的稳健性和精确性。
参考文献:
[1] 王睿,王洪财.Miro1蛋白在帕金森病发病中的作用 [J].临床神经病学杂志,2023,36(2):151-154.
[2] 孙康明,季红,宋菲菲,等.远程医疗在帕金森病病人中的应用研究进展 [J].护理研究,2023,37(5):860-864.
[3] 赵经纬,薛峥,李静怡,等.C-C趋化因子配体5通过诱导帕金森病模型小鼠外周Th17细胞比例增加、Treg细胞比例减少及促进Th17细胞表达淋巴细胞功能相关抗原1而加重神经炎症的研究 [J].临床神经病学杂志,2023,36(2):134-141.
[4] 谭丽.中晚期帕金森病脑深部电刺激治疗前后中医证候特征研究 [D].北京:北京中医药大学,2021.
[5] 李函芮,秦丽微.经颅多普勒超声与头颅核磁检查对帕金森病患者的诊断价值 [J].医学信息,2023,36(6):106-109.
[6] 臧一腾,陈思臻,陆贝尔,等.基于线性混合模型树在体质指数纵向轨迹中的应用 [J].中国卫生统计,2024,41(1):41-44.
[7] 吴喜之,张敏. 应用回归及分类——基于R与Python的实现:第2版 [M]. 北京:中国人民大学出版社,2020,10.
[8] PANOKIN N V,AVERIN A V,KOSTIN I A,et al. Method for Sparse Representation of Complex Data Based on Overcomplete Basis,L1 Norm,and Neural MFNN-like Network [J].Applied Sciences,2024,14(5):1959(2024-02-27). https://doi.org/10.3390/app14051959.
[9] 于秀君.稀疏主成分分析与BP神经网络结合算法及其在心脏病临床数据分析中的应用 [D].昆明:云南师范大学,2022.
[10] 田子文. 基于正则化与神经网络的溶解氧浓度预测控制算法研究 [D].西安:陕西科技大学,2024.
[11] LAIED N,WARE J. Random-effects Models for Longitudinal Data [J].Biometrics,1982(38):963-974.
[12] SAKAR C O,SERBES G,GUNDUZ A,et al. A Comparative Analysis of Speech Signal Processing Algorithms for Parkinsons Disease Classification and the Use of the Tunable Q-Factor Wavelet Transform [J].Applied Soft Computing,2019,74:255-263.
[13] ROTHLIND J C,YORK M K,LUO P,et al. Predictors of Multi-Domain Cognitive Decline Following DBS for Treatment of Parkinsons Disease [J].Parkinsonism amp; Related Disorders,2021,95:23-27.
作者简介:罗成敏(1998—),女,汉族,云南临沧人,硕士研究生在读,研究方向:生物统计:王涛(1964—),男,汉族,云南昆明人,教授,硕士研究生,研究方向:生物统计。
基金项目:国家自然科学基金资助项目(81360449);云南师范大学研究生科研训练基金项目(YJSJJ23-B105)