

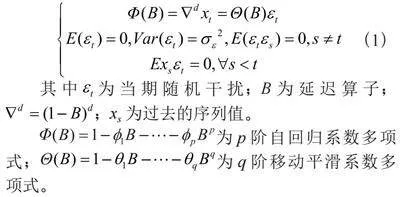
摘" 要:对金融时间序列数据的研究一直广受关注,特别是股票的价格研究。文章以上证指数的开盘价为研究对象,运用ARIMA模型、ARIMA-LSTM模型以及ARIMA和ARIMA-LSTM组合模型对股票开盘价进行10天、50天、116天预测,计算每个模型的拟合优度R2,平均绝对误差MAE和均方根误差RMSE。通过比较三个模型的三个统计指标,最后得到在10天预测值时,ARIMA模型预测较好,当预测时间加长时ARIMA-LSTM模型以及ARIMA和ARIMA-LSTM组合模型表现比ARIMA模型好。
关键词:预测;ARIMA模型;ARIMA-LSTM模型;ARIMA和ARIMA-LSTM组合模型
中图分类号:TP18" " 文献标识码:A" 文章编号:2096-4706(2024)21-0041-05
Stock Analysis Based on ARIMA and LSTM Models
HE Jie1, LI Suping2, HE Yingying1, SUN Yanan1, QIN Xiaojiang1
(1.Chongqing College of Humanities, Science and Technology, Chongqing" 401524, China;
2.Chongqing Institute of Engineering, Chongqing" 400056, China)
Abstract: The research on financial time series data has always received widespread attention, especially in the research on stock prices. Taking the opening price of the Shanghai Securities Composite Index as the research object, this paper uses ARIMA model, ARIMA-LSTM model, and ARIMA and ARIMA-LSTM combination model to predict the opening price for 10 days, 50 days and 116 days, and calculates the R2, MAE and RMSE for each model. By comparing the three statistical indicators of the three models, it is found that the ARIMA model predicts better at 10 days. When the prediction time is extended, the ARIMA-LSTM model and the ARIMA and ARIMA-LSTM combination model performs better than the ARIMA model.
Keywords: prediction; ARIMA model; ARIMA-LSTM model; ARIMA and ARIMA-LSTM combination model
0" 引" 言
目前越来越多的人选择投资股票以获得经济利益,为获得丰厚的经济利益,投资者在作出决策之前都会对选取的股票进行研究或者预测其走势。而股票价格数据是比较典型的金融时间序列,使用股票的历史价格数据建立预测模型,对未来股票价格进行预测[1]。对金融时间序列的研究出现了很多相关的模型和方法,并得到一些可靠的结论,为投资者做选择提供了参考。
王莹[2]以中国银行股票为例,运用ARMA模型对股票开盘价进行了短期分析和预测,并得出预测值与实际值相近,误差较小。刘洁[3]用ARMA模型对格力电器的股票价格进行预测,该模型在短期预测中效果较好。吴玉霞[4]等人基于ARIMA模型对“华泰证劵”的收盘价进行了短期预测,认为ARIMA模型短期动态、静态预测较好。有学者在ARIMA模型基础上衍生了其他模型,如熊政[5]构造了ARIMA-GARCH-M模型,在股票短期预测中有着良好的效果。方燕[6]等人用ARIMA-GARCH模型对传媒板块指数进行预测,认为ARIMA-GARCH模型可用于具有“尖峰厚尾”分布特征的股票进行预测。以上的研究都是基于ARIMA模型或ARIMA模型的组合模型对股票进行短期的预测,达到的效果都较好。基于金融时间序列,徐卫泽[7]比较了ARIMA模型和LSTM模型,并得出结论LSTM模型的准确性优于ARIMA模型。因此,很多学者将ARIMA模型和LSTM模型组合在一起运用,得到的预测比单一模型更好[8]。次必聪[9]等人,用ARIMA模型、线性ARIMA-LSTM模型和非线性ARIMA-LSTM模型,对道琼斯工业指数做了短期、中期和长期的预测,并得到非线性组合模型得到的预测优于单一模型。
基于以上学者的研究,在ARIMA模型和线性ARIMA-LSTM模型的基础上构造一种新的线性模型,即ARIMA和ARIMA-LSTM组合模型。用ARIMA模型和线性ARIMA-LSTM模型构造的组合模型分别预测上证指数的开盘价,得到各个模型的拟合优度(R2)、MAE、RMAE,比较统计指标,选取最优模型。
1" 模型简介
1.1" ARIMA模型
ARIMA模型称为求和自回归移动平均模型(记ARIMA(p,d,q)),ARIMA模型是在ARMA模型的基础上产生的。分析平稳时间序列用ARMA模型,非平稳时间序列若经过差分后平稳可以用ARIMA模型。
p为自回归模型的阶数,q为移动平均模型阶数,d为ARMA模型差分的阶数,模型为:
(1)
其中为当期随机干扰;B为延迟算子;;xs为过去的序列值。
为p阶自回归系数多项式;为q阶移动平滑系数多项式。
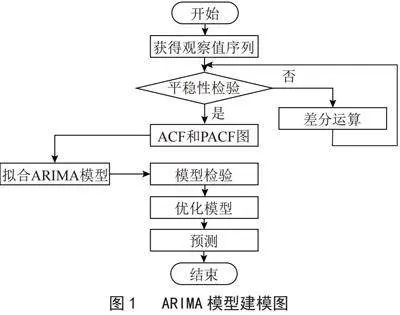
ARIMA模型建模步骤:第一步,检验时间序列数据的平稳性和纯随机性,若时间序列数据是平稳非白噪声序列则可拟合ARIMA模型;若时间序列数据是非平稳数据,可对数据进行差分运算,再进行平稳性和纯随机性检验,检验通过后则可拟合ARIMA模型。第二步,绘制自相关图和偏自相关图,根据自相关图和偏自相关图的特点对模型进行定阶,识别模型,可以识别多个合理的模型。第三步,对识别的模型进行检验(包括残差序列的纯随机性检验和参数及模型的显著性检验)。第四步,优化模型,根据AIC和BIC值选取最优模型。第五步,利用选取的模型进行预测。流程图如图1所示。
1.2" ARIMA-LSTM模型
将时间序列数据分为线性和非线性两个部分,用ARIMA模型分析线性部分得Lt,用LSTM模型分析非线性部分得Nt,则得到时间序列预测表达式[10]:
(2)
其中xt为时间序列,Lt为时间序列的线性部分的分量,Nt为时间序列的非线性部分的分量。
预测步骤如下:用ARIMA模型对原始数据进行拟合得到预测值,再用真实值xt减预测值得到残差序列,利用LSTM模型对残差序列进行预测得到 ,即:
(3)
其中为ARIMA-LSTM模型的预测值。
1.3" ARIMA和ARIMA-LSTM组合模型
基于ARIMA和ARIMA-LSTM两种模型,现构造一种ARIMA和ARIMA-LSTM组合模型,ARIMA模型拟合时间序列并得到时间序列的预测值,
可得到ARIMA模型拟合优度,ARIMA-LSTM模型拟合时间序列并得到时间序列的预测值,可得到模型拟合优度,即组合模型为:
(4)
其中为组合模型的预测值,ARIMA weight为ARIMA的权重值,ARIMA-LSTMweight为ARIMA-LSTM的权重值即:,。
1.4" 预测结果评价标准
为有效地评价模型,选取平均绝对误差、均方根误差及决定系数(拟合优度)三个指标对模型进行评价,如下所示。
平均绝对误差:
(5)
均方根误差:
(6)
决定系数(拟合优度):
(7)
其中N为时间序列长度,xi为真实值,为预测值,为真实值的平均值。平均绝对误差和均方根误差的值越小越好,决定系数(拟合优度)的值越接近1数据越真实。
2" 实证分析
2.1" 数据及软件的选取
本文选取上证指数2021年1月4日到2024年3月27日的股票数据,运用的R软件和SPSS对上证指数的开盘价进行分析和预测。利用2021年1月4日到2023年9月28日上证指数的开盘价作为试验数据建立模型,对2023年10月9日到2024年3月27日上证指数开盘价进行预测。
2.2" ARIMA模型
2.2.1" 平稳性和纯随机性检验
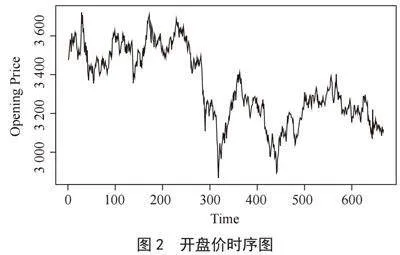
在建立模型之前,应对股票开盘价进行平稳性检验,画出时序图根据时序图的波动判断序列数据的平稳性,如图2所示。
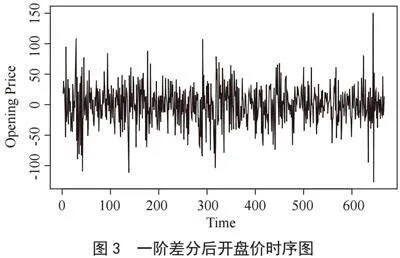
图2显示,原始数据的波动较大,即不是平稳序列,要对原始数据进行差分处理。经过一阶差分后得到图3,图3可以看出,原始数据一阶差分后的值围绕0值上下波动,即认为一阶差分后的数据是平稳的。再对差分后的数据进行白噪声检验,得到p值为0.001 624小于0.05,故差分后的股票数据是非白噪声数据,能进行ARIMA建模。
图3" 一阶差分后开盘价时序图
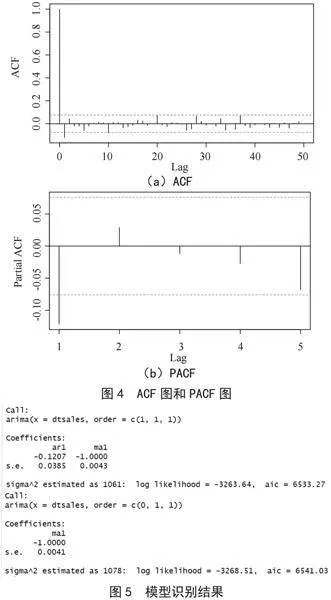
2.2.2" 自相关图、偏自相关图及模型定阶
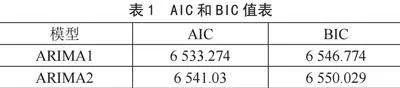
用差分后的股票数据,绘制自相关图和偏自相关图如图4所示。根据自相关图和偏自相关图,确定了模型ARIMA(1,1,1)和ARIMA(0,1,1),如图5所示。
2.2.3" 模型检验
确定模型后,对两个模型进行检验,首先由图5中的各个估计参数除以其标准差的绝对值都大于1.96,故认为两个模型系数是显著的;再对残差进行纯随机性检验,如图6所示,ARIMA(1,1,1)残差检验的p值为0.28大于0.05,故认为残差序列为白噪声序列,残差之间不存在序列相关性,该模型较好。ARIMA(0,1,1)残差检验的p值为0.02小于0.05,残差序列存在序列相关性,认为该模型提取信息不够完整,需要进一步处理。
2.2.4" 优化模型
对模型进行检验后,在两个模型中要选择最优模型,计算两个模型的AIC和BIC值,其值越小越好,如表1所示。ARIMA(1,1,1)模型的AIC和BIC值分别为6 533.274和6 546.774,都比ARIMA(0,1,1)AIC和BIC值小,进一步验证选取模型ARIMA(1,1,1)。
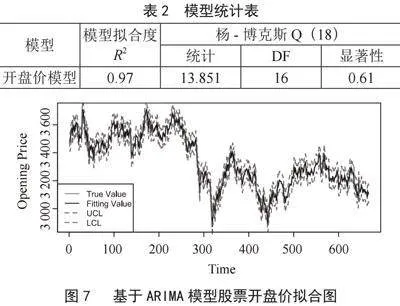
2.2.5" 模型拟合
通过以上检验及分析,最后选取的模型为ARIMA(1,1,1),用SPSS软件,运用该模型模拟上证指数2021年1月4日到2023年9月28日的开盘价,通过分析得到表2及图7。如表2所示,拟合模型的R2为0.97且显著性的概率为0.61(p值大于0.05,表示模型拟合合理)。如图7所示,股票开盘价的真实数据和拟合数据几乎重合且都在95%的置信区间内,故认为模型拟合较好。
2.3" ARIMA-LSTM模型
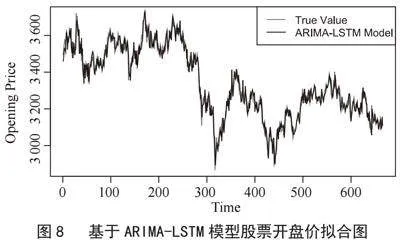
用R软件,使用ARIMA-LSTM模型模拟上证指数2021年1月4日到2023年9月28日的开盘价。计算得到拟合模型的R2为0.96,R2较大且接近1,并得到股票开盘价的真实数据和拟合数据的折线图,如图8所示,开盘价和拟合值几乎重合,故该模型拟合较好。
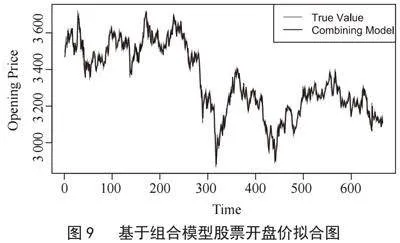
2.4" ARIMA和ARIMA-LSTM组合模型
利用ARIMA模型对原始数据进行拟合得拟合值,ARIMA-LSTM模型对原始数据进行拟合得拟合值,根据式(4)计算得到ARIMA和ARIMA-LSTM组合模型的拟合值,计算得到组合模型的R2为0.97。得到真实数据和拟合数据的折线图,如图9所示,由图显示真实开盘价和拟合开盘价波动几乎相同。
2.5" 预测结果
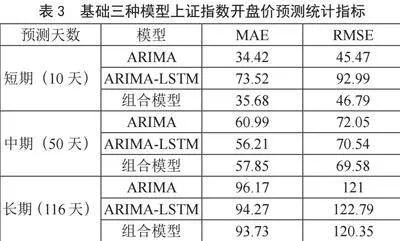
基于以上三种模型预测了上证指数10天、50天、116天的开盘价,并计算三种模型不同预测天数的MAE、RMSE值,如表3所示。
由表3可知,同一个模型,当预测的时间增加时,预测的准确度下降,MAE和RMSE值几乎都相应增大。预测天数为10天时,ARIMA模型和组合模型预测效果较好,MAE和RMSE值都相对较小,在10天的预测中效果最好的是ARIMA模型。在50天的预测中,与10天预测相比预测精度下降,但ARIMA-LSTM模型的MAE和RMSE值与10天预测相比之下变小,总体来说,与ARIMA模型相比,ARIMA-LSTM模型和组合模型预测较好。当预测天数增加到116天数时,所有模型的MAE和RMSE值都较大,相对比较组合模型的MAE和RMSE值较小,故对于长期预测更偏向选取组合模型。
3" 结" 论
上述分别用三个模型对上证指数2021年1月4日到2023年9月28日的股票开盘价进行了模拟和分析,并对以后10天、50天、116天的开盘价进行预测。在短期的预测中,使用ARIMA模型进行预测较好;在中期的预测中,可以使用ARIMA-LSTM模型或者组合模型;在长期预测中,所有模型的预测精度都下降,但组合模型的预测相对较好,对上证指数收盘价的预测有一定的指导性。
本文运用了ARIMA模型、ARIMA-LSTM模型、ARIMA和ARIMA-LSTM组合模型,利用三个模型对上证指数的开盘价进行分析和预测,并得到相应的结论。在考虑组合模型时,以ARIMA模型和ARIMA-LSTM模型的R2算比重作为系数,用线性组合的形式得到组合模型。在以往学者的研究中显示非线性组合模型的预测比线性组合模型的预测效果好,因此在以后的研究中可以考虑ARIMA和ARIMA-LSTM组合非线性的组合模型。
参考文献:
[1] HE Y,LI J M,RUAN S M,et al. A Hybrid Model for Financial Time Series Forecasting—Integration of EWT, ARIMA with the Improved ABC Optimized ELM [J].IEEE Access,2020,8:84501-84518.
[2] 王莹.基于ARMA模型的股票价格的分析及预测 [J].生产力研究,2021(9):124-127.
[3] 刘洁.ARMA模型在股票价格预测中的应用——以格力电器为例 [J].中国管理信息化,2021,24(11):153-155.
[4] 吴玉霞,温欣.基于ARIMA模型的短期股票价格预测 [J].统计与决策,2016(23):83-86.
[5] 熊政,车文刚.ARIMA-GARCH-M模型在短期股票预测中的应用 [J].陕西理工大学学报:自然科学版,2022,38(4):69-74.
[6] 方燕,耿雪洋,秦珊珊.沪深两市传媒板块指数价格预测研究——基于ARIMA—GARCH模型的分析 [J].价格理论与实践,2018(1):102-105.
[7] 徐卫泽.预测经济和金融时间序列:ARIMA与LSTM模型的比较 [J].山西农经,2020(3):36-37.
[8] SUN Y,ZHAO Z J,MA X B,et al. Short-time Scale Gravitational Microlensing Events Prediction with ARIMA-LSTM and ARIMA-GRU Hybrid Model [C]//BigSDM: International Conference on Big Scientific Data Management.Beijing:Springer,2018:224-238.
[9] 次必聪,张品一.基于ARIMA-LSTM模型的金融时间序列预测 [J].统计与决策,2022,38(11):145-149.
[10] ZHANG G P. Time Series Forecasting Using a Hybrid ARIMA and Neural Network Model [J].Neurocomputing,2003,50:159-175.
作者简介:何杰(1993—),女,汉族,重庆大足人,讲师,硕士,研究方向:应用统计;李素平(1993—),男,汉族,重庆云阳人,讲师,硕士,研究方向:应用统计;何盈盈(1994—),女,汉族,重庆涪陵人,讲师,硕士,研究方向:大数据;孙亚南(1992—),男,汉族,河南清丰人,讲师,硕士,研究方向:大数据;秦晓江(1982—),女,汉族,重庆人,副教授,硕士,研究方向:无线定位。
基金项目:重庆人文科技学院科学研究项目(JSJGC202205);重庆人文科技学院科学研究项目(JSJGC202201);重庆人文科技学院科学研究项目(JSJGC202202)