






摘" 要:针对传统安时积分法估算锂电池荷电状态(SOC)存在精度不足的问题,文章提出一种优化开路电压-安时积分法(OCV-AH)的锂电池SOC估计算法。该优化OCV-AH积分法主要包括静态SOC初始值的校正和动态安时积分法的优化。首先将静置法数据分段拟合涓流放电曲线,得到高精度的OCV-SOC特性曲线作为校正SOC初始值的依据;然后在考虑了温度、放电倍率和充放电循环次数对电池实际容量的影响后,计算出修正系数,加入安时积分法中,动态修正电池的实际容量。最后,在Simulink中搭建了优化OCV-AH积分法的模型,并在DST工况下,将优化安时积分法与传统安时积分法进行仿真对比,验证了该文设计的优化OCV-AH积分法对于SOC初始值校正和SOC动态估算的精确性。
关键词:SOC估计;优化OCV-AH积分法;OCV-SOC特性曲线;修正系数
中图分类号:TM912" " 文献标识码:A" 文章编号:2096-4706(2024)21-0011-06
SOC Estimation Based on Optimized OCV-AH Integration Method
TAO Zhengshun, HU Guanyang
(School of Internet of Things Engineering, Jiangnan University, Wuxi" 214122, China)
Abstract: In response to the problem of insufficient accuracy in estimating the State of Charge (SOC) of lithium batteries using traditional Ampere-hour integration method, this paper proposes an optimized Open Circuit Voltage-Ampere Hour integration method (OCV-AH) for SOC estimation algorithm of lithium batteries. The optimized OCV-AH integration method mainly includes the correction of static SOC initial values and the optimization of dynamic Ampere-hour integration method. Firstly, the static method data is segmented to fit the trickle discharge curve, and a high-precision OCV-SOC characteristic curve is obtained as the basis for correcting the initial SOC value. Then, after considering the effects of temperature, discharge rate, and number of charge discharge cycles on the actual capacity of the battery, a correction coefficient is calculated and added to the Ampere-hour integration method to dynamically correct the actual capacity of the battery. Finally, this paper builds a model of optimized OCV-AH integration method in Simulink, and compares the optimized Ampere-hour integration method with the traditional Ampere-hour integration method through simulation under the DST working conditions, verifying the accuracy of the optimized OCV-AH integration method designed in this paper for correction of initial SOC value and SOC dynamic estimation.
Keywords: SOC estimation; optimized OCV-AH integration method; OCV-SOC characteristic curve; correction coefficient
0" 引" 言
锂电池因其具有能量密度高、自放电率低、循环使用寿命长等优点,逐渐在储能系统和动力系统中得到广泛应用[1]。为了提升电池的使用效率,并保障安全性,实时且精准地估算锂电池的荷电状态(SOC)就显得格外重要。但是锂电池内部的化学反应是一个高度复杂的电化学系统,很容易受到充放电次数、环境温度、充放电倍率的影响,从而呈现出很强的非线性[2],这就为SOC的精确估算带来了很大挑战。目前常见的SOC估计方案主要有开路电压法、安时积分法、卡尔曼滤波法以及神经网络法等。开路电压法(Open Circuit Voltage, OCV),是用开路电压来衡量电池荷电状态的方法,需要大量时间将电池静置到电压稳定状态,故而不适用对SOC的实时估算[3-4]。滤波法和神经网络法虽然估算的精确度较高,都存在着算力要求大、计算复杂程度高、估算时间长等缺点,实用性较差[5]。
而安时积分法因其不需要复杂的计算和模型,只需实时地对电池充放电过程中的电流进行积分,因此具有很好的实时性,适用于实时监测和控制应用。但同时在实际应用中,特别是长时间运行或者频繁充放电后,安时积分法往往会受到积分误差的累积影响导致SOC估计的偏差增大[6-7],故而需要对其进行修正,以提高对SOC估计的精度。
本文针对传统安时积分法估算SOC误差大的问题,提出了优化OCV-AH积分法,分别从静态初始SOC校正和动态安时积分法的修正角度入手,解决安时积分法在实际使用中误差较大的问题。
1" 高精度OCV-SOC 特性曲线的获取
1.1" 涓流放电曲线的分段拟合
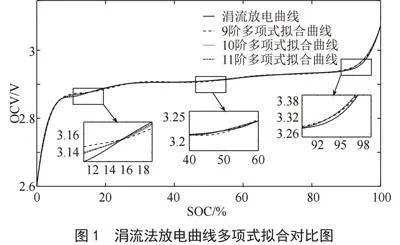
涓流放电曲线的拟合精度对OCV-SOC曲线的优化效果有着重要影响。图1给出的是锂电池涓流放电曲线及其多项式拟合结果。从结果中可以观察到,当使用多项式直接拟合锂电池的涓流放电曲线时,由于受到其中特殊电压环节(如电压平台期、电压陡变)的影响,拟合效果在局部SOC区域内往往不是很理想。
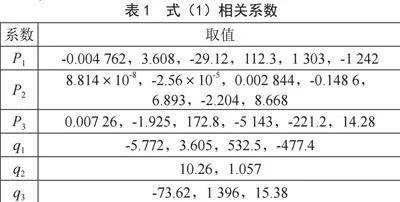
为了提升锂电池涓流放电曲线的拟合精度,采用分段拟合的方式[8],将待拟合曲线根据涓流放电曲线的特性,选取SOC在25%和90%为分段点,分为三段,分别选择拟合精度较高的拟合形式。拟合结果为式(1),相关系数如表1所示。
(1)
1.2" OCV-SOC曲线优化
在电池涓流放电过程中,由于工作电流较小,电池特性相对稳定,本文选择Thevenin模型来分析电池放电过程中的极化效应机理。
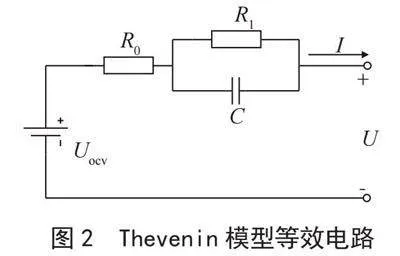
如图所示,其中Uocv表示电池的开路电压,R0、R1、C则分别表示电池的欧姆内阻、极化内阻和极化电容。
图2" Thevenin模型等效电路
在涓流法测试中,采集的涓流放电电压未包含了微小的极化电压,且由于放电前半程,电池的工作电流较小且电池特性稳定,可以将Thevenin模型的参数(R0、R1、C)视为恒定不变的值。故而可写出如下表达式:
(2)
其中w1=R0I,w2=R1I,都表示待确定的优化系数,m=R1C则表示未知常数。
(3)
其中,Q表示锂电池额定容量。Η表示充放电效率,在电池恒流放电工况下,可看作恒定,则式(3)可写为:
(4)
其中h表示常数,将式(4)带入式(2)可得:
(5)
其中,w3 = mh表示待确定的优化系数,用来模拟涓流极化电压的变化过程。
在涓流放电后期,电池特性也会发生急剧变化。R0、R1、C等参数无法保持恒定不变,这导致式(5)无法准确描述电池特性的变化趋势。在电池SOC低于30%时,电池的电压变化可以叠加经验公式来描述。
(6)
其中,Ujh表示叠加的极化电压,w4、w5为设立的待确定优化系数。则全SOC阶段的优化方程可表示为:
(7)
1.3" 目标函数及寻优算法
在以上所述的优化方程基础上,将涓流放电曲线与静置法放电在相应SOC测试点处电压差之和最小化作为优化目标,则目标函数可表示为:
(8)
其中,Ust(i)表示静置法在第i个SOC测试点处的电压值,而Uocv(i)则表示OCV-SOC优化曲线在第i个SOC测试点处的电压值。约束条件是将涓流放电曲线和静置法在相应SOC测试点处的电压进行对比。
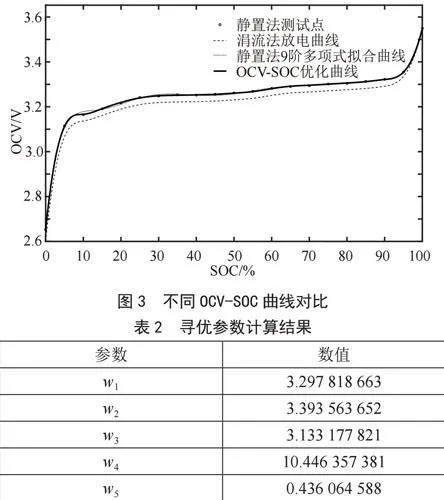
最后采用自适应遗传算法(Differential Evolution, DE)作为优化算法,求取处各个优化参数,以获取OCV-SOC优化曲线。使用上述优化算法对分段形式拟合的涓流放电曲线进行优化后,得到如图3所示的OCV-SOC优化曲线,同时求得的优化系数如表2所示。
2" 优化安时积分法估算SOC
在诸多估算SOC的算法中,安时积分法对算力要求不高,有着很好的实用性,但同时安时积分法只考虑了充放电电流对时间的积分,而忽略了外界因素的影响,估算误差会不断积累,故而须结合放电倍率、温度、循环次数等因素进行修正,以提高对SOC估计的精度[9]。
2.1" 放电倍率对锂离子电池容量的影响
由于锂电池内部存在一定的内阻,放电倍率增大会导致更多的电量被内阻消耗,因此,电池的放电倍率对其容量有显著影响。
引用如式(9)所示的Peukert公式来修正放电倍率变化引起的电池容量变化[10]:
(9)
其中:I表示放电电流,t表示时间,n和K表示常数,由电池本身决定。由式(9)可以推导出放电倍率修正系数计算公式[11],如式(10)所示:
(10)
其中:CI表示锂电池放电电流为I时,实际释放的电量。
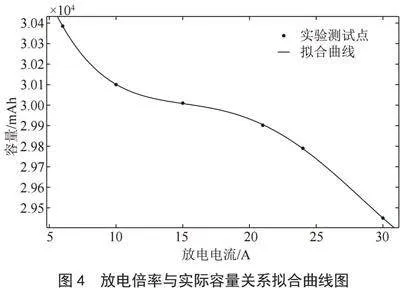
根据锂电池厂家的测试数据,可得到如图4所示的锂电池在0.2C、0.33C、0.5C、0.7C、0.8C和1C放电倍率下通过MATLAB处理得到的电池实际可用容量随放电倍率变化的拟合曲线,结合公式(10)可得到放电倍率修正系数的公式:
(11)
2.2" 温度对锂离子电池容量的影响
随着环境温度的变化,电池的实际可用容量表现出非线性的变化特性。为了修正环境温度对电池可用容量的影响,我们引入了环境温度修正系数ηT。因此,修正后的电池可用容量可表示为:
(12)
式中:CT表示环境温度为T时电池的实际可放出的容量
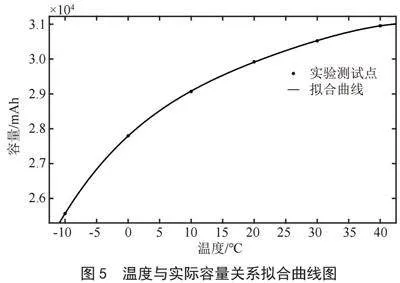
根据电池厂家温度特性测试数据,使用MATLAB对电池实际可用容量随环境温度变化的数据进行处理,得到了如图5所示拟合曲线。则可求得电池对应的环境温度修正系数:
(13)
2.3" 充放电循环次数对锂离子电池容量的影响
随着锂电池充放电循环次数的增加,活性物质慢慢损失,主要表现为SEI膜的生成、分解和增长,以及正负极内活性颗粒的损坏和内部晶格的塌陷,这也是老化电池容量减少的主要原因。
引入电池老化修正系数ηh,用以描述循环次数与电池实际可用容量之间的关系,则:
(14)
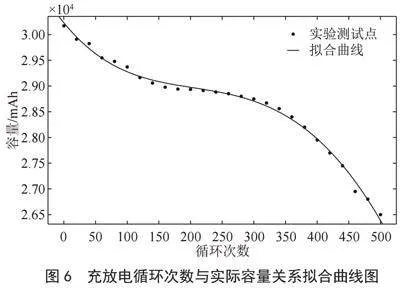
式中:Ch表示电池第h次循环后的实际可用容量。电池厂家关于电池老化特性测试的拟合曲线如图6所示。则电池老化修正系数的可表示为:
(15)
3" 优化OCV-Ah积分法估算SOC
在得到OCV-SOC特性曲线和温度、放电倍率以及循环次数对容量的修正系数后,优化OCV-Ah积分法的计算公式可表示为:
(16)
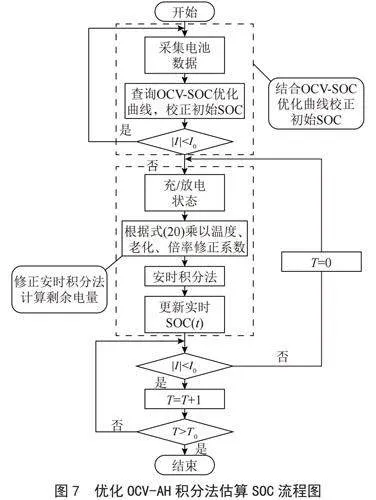
其中SOC(0)为电池的初始SOC,可根据静置的开 路电压查询OCV-SOC优化曲线获得。优化OCV-AH积分法估算锂电池SOC具体过程如图7所示。
4" 仿真验证及结果分析
为了验证本文设计的优化OCV-AH积分法对SOC的估计具有较高的精度,本文基于Simulink平台搭建优化安时积分法的估算模型,通过DST工况下的运行数据对优化OCV-AH积分法进行仿真验证,同时将传统安时积分法在DST工况下的仿真波形作为对比进行更全面的分析。本文的本论文优化安时积分法是采用高精度OCV-SOC特性曲线作为静态初始SOC校正,并结合考虑温度等因素的修正安时积分法;传统安时积分法是采用静置法的9阶拟合曲线作为静态初始SOC校正,并结合普通安时积分进行动态SOC估算。
4.1" SOC的初始值校正精度的验证
设置电池SOC的初始值为87%,来验证两种算法对SOC初始值校正的准确性。
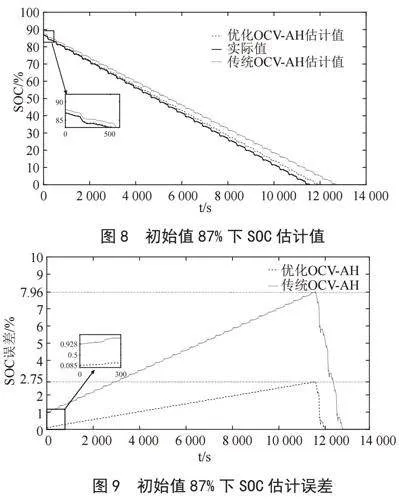
图8、9分别为SOC初始值87%时SOC真实值与两种算法的估算值对比图,以及对应的误差图。从该图中不难看出,在电池运行的初始阶段,两种算法估计的SOC曲线与真实值之间贴合的非常紧密,但是随着时间的推移估计值与真实值之间的误差逐渐显露。不过虽然两种算法的在运行后期与真实值之间都是存在偏差,相对于传统OCV-AH,优化后的安时积分法显然更加贴合SOC估计的真实值。
图9中优化OCV-AH的估算的初始值误差很小只有0.085%,而传统OCV-AH对SOC初始值估算的误差已经达到0.928%,是优化OCV-AH估算误差的10倍,这是因为87%并非静置法的采样点,故而在该点传统安时积分法对于SOC初始值的校正误差较大。而优化OCV-AH采用了本文设计的高精度OCV-SOC特性曲线,在非静置法采样点依然有着较高的精度。
4.2" 温度影响SOC估算精度的验证
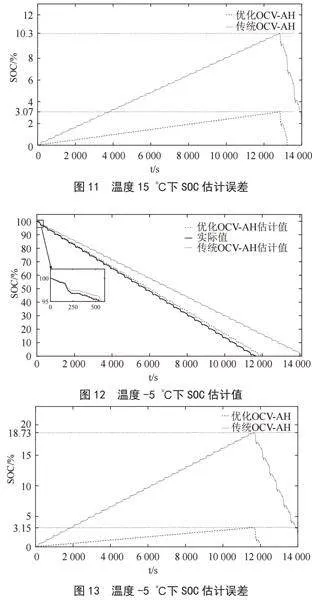
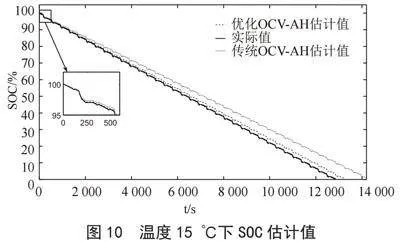
分别设置环境温度为15 ℃和-5 ℃,来验证两种算法对SOC估算精度的验证。图10、12分别为温度在15℃和-5℃时,SOC真实值与两种算法的估算值对比图,图11、13分别为对应的误差图。不难看出,温度由15℃下降到-5℃,优化OCV-AH估算估计曲线与真实值仍然是较为贴合,最大误差也只是在3.1%左右,而传统OCV-AH却逐渐偏离真实值曲线,最大误差也从10.3%增长到了18.7%体现了优化OCV-AH在温度变化时估算SOC仍有较高的精度。
5" 结" 论
本文针对传统安时积分法估算精度较差的问题,设计了基于优化安时积分法的电池管理系统,并对其工作流程进行了详细设计,包括静态SOC初始值校正和动态安时积分法的优化。通过静置法分段拟合涓流放电曲线,得到了高精度的OCV-SOC特性曲线作为校正SOC初始值的依据;而后接着在考虑了温度、放电倍率和充放电循环次数对电池实际容量的影响后,计算出修正系数,加入安时积分法中,动态修正电池的实际容量;最后在DST工况下将优化OCV-AH与传统OCV-AH进行仿真对比,验证了本文设计的优化安时积分法对于SOC初始值校正和SOC估算的精确性。
参考文献:
[1] 傅军栋,陈浩杰,孙翔,等.基于多Agent的锂电池主动均衡策略控制仿真研究 [J].华东交通大学学报,2024,41(1):96-104.
[2] 朱磊.电动汽车锂电池SOC估计及均衡控制策略研究 [D].无锡:江南大学,2022.
[3] 罗勇,祁朋伟,黄欢,等.基于容量修正的安时积分SOC估算方法研究 [J].汽车工程,2020,42(5):681-687.
[4] SNIHIR I,REY W,VERBITSKIY E,et al. Battery Open-circuit Voltage Estimation by a Method of Statistical Analysis [J].Journal of Power Sources,2005,159(2):1484-1487.
[5] 汪锋.基于修正安时积分法SOC估算的电池管理系统设计 [D].长沙:湖南大学,2020.
[6] OZCAN G,PAJOVIC M,SAHINOGLU Z,et al. Online Battery State-of-charge Estimation Based on Sparse Gaussian Process Regression [C]//2016 IEEE Power and Energy Society General Meeting (PESGM),Boston:IEEE,2016:1-5.
[7] MENG J H,LUO G Z,GAO F. Lithium Polymer Battery State-of-charge Estimation Based on Adaptive Unscented Kalman Filter and Support Vector Machine [J].IEEE Transactions on Power Electronics,2016,31(3):2226-2238.
[8] 林加顺,周娟,吴乃豪,等.一种高精度磷酸铁锂电池OCV-SOC曲线获取方法 [J].电源学报.
[9] 邢厚超.基于修正开路电压-安时积分法的电池管理系统研究 [D].盐城:盐城工学院,2022.
[10] 仝猛,卢兰光,欧阳明高,等.Peukert方程的适用性分析及基于二阶段放电法的Peukert模型修正 [J].机械工程学报,2010,46(10):121-125.
[11] 高金辉,朱元培,刘永.用一种新的优化算法估计电动汽车电池SOC [J].电源技术,2014,38(1):75-77.
作者简介:陶正顺(1998—),男,汉族,江苏盐城人,硕士研究生在读,研究方向:新能源储能技术。