


摘 要:黄河水沙通量的变化规律对沿黄流域的环境治理、气候变化和人民生活具有深远的影响。文章以黄河某水文站2016—2021年的水位、水流量与含沙量的实际监测数据为研究对象,对该水文站水沙通量的变化规律进行挖掘和分析;以此应用机器学习中的时间序列分析算法构建了一种可对黄河水沙通量趋势预测的时间序列模型SARIMAX,通过对模型的参数优化和显著性检验分析,确定了黄河水沙通量预测的最优时间序列模型SARIMAX(0,1,1,12),对该水文站未来两年的黄河水沙通量进行了分析预测,为黄河水文环境的保护和黄河水域“调水调沙”等工作提供准确的参考依据。
关键词:时间序列模型;ARIMA;水沙通量;机器学习
中图分类号:TP391.1 文献标识码:A 文章编号:2096-4706(2024)20-0159-06
Research on the Analysis of Yellow River Water and Sediment Monitoring Data Based on Time Series Model
LI Changsheng, LIU Sujun, LIU Zongcheng, LIU Xiaolong
(Lanzhou Petrochemical University of Vocational Technology, Lanzhou 730060, China)
Abstract: The variation law of water and sediment flux in the Yellow River has a profound impact on environmental governance, climate change, and peoples lives along the Yellow River basin. This paper takes the actual monitoring data of water level, water flow rate, and sediment concentration at a hydrological station on the Yellow River from 2016 to 2021 as the research object, and explores and analyzes the variation law in water and sediment flux at the hydrological station. A Time Series Analysis algorithm in Machine Learning is applied to construct a Time Series Model SARIMAX that can predict the trend of Yellow River water and sediment flux. Through parameter optimization and significance testing analysis of the model, the optimal Time Series Model SARIMAX (0, 1, 1, 12) for predicting Yellow River water and sediment flux is determined. The Yellow River water and sediment flux of the hydrological station in the next two years is analyzed and predicted, providing accurate reference for the protection of the Yellow River hydrological environment and the work of “water and sediment transfer” in the Yellow River water area.
Keywords: Time Series Model; ARIMA; water and sediment flux; Machine Learning
0 引 言
黄河是中华民族的母亲河。研究黄河水沙通量的变化规律对沿黄流域的环境治理、气候变化和人民生活具有深远的影响,同时也对优化黄河流域水资源分配、协调人地关系、调水调沙、防洪减灾等方面都具有重要的理论指导意义。
近年来在黄河水、沙、环境问题的研究方面,褚言皓等人利用最优遥感反演算法,基于小时分辨率特征开展了GOCI遥感影像研究,研究了黄河水域悬浮泥沙时空动态特征和驱动机制[1];王俊杰等人对水沙时间序列的变异性进行了分析,通过滑动T检验、曼尼-肯德尔检验法、5a滑动平均法等,研究了水沙通量的趋势[2];刘明等挖掘了水文站“调水调沙”期间黄河入海泥沙中Pb元素含量及其同位素组成的变化特征,并通过对利津水文站悬浮泥沙分析、小浪底水库表层沉积物分析、物质来源及对“调水调沙”过程的影响[3]等。
这些关于黄河水、沙、环境的统计分析方法虽然在技术方法上取得了一定的进步,但大多数研究缺少对黄河水域水沙通量的突变性、季节性和周期性的分析,或采用单变量时序预测模型未能充分考虑水沙通量的周期性变化和“调水调沙”措施等环境因素影响。因此本文旨在基于黄河流域水沙通量的实际历史监测数据的多因素相关性和时序相关性分析,首先,利用机器学习算法从水文站的水沙通量的突变性、季节性和周期性三个方面,分别应用水沙通量时序关系图、季节性分解的局部回归方法(STL)、水沙通量自相关系数(ACF)对水沙通量的变化进行了分析,挖掘了该水文站水沙通量的变化规律;其次,基于时间序列分析算法构建了该水文站水沙通量的时间序列模型SARIMAX,并通过网格搜索算法对SARIMAX模型的参数进行了优化,确定了最优模型SARIMAX(0,1,1,12);最后,根据该模型对未来两年的黄河水沙通量进行了分析预测,使水文站既能及时掌握水沙通量的动态变化情况,又能最大限度地减少监测成本资源。
1 水沙通量的探索性数据分析
1.1 数据概述
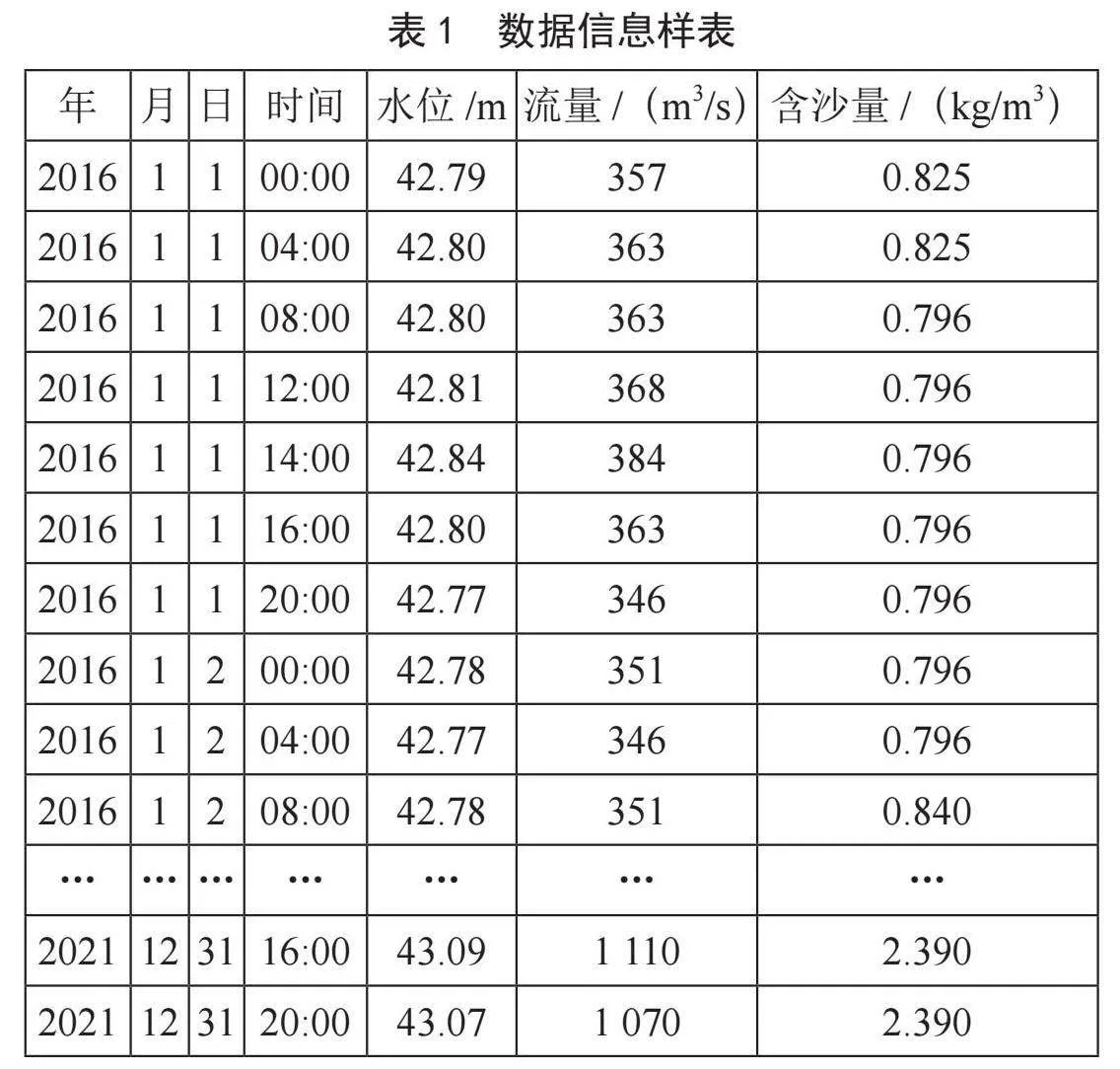
本文数据集来源于“2023年全国大学生数学建模竞赛E题[4]”中黄河小浪底水库下游某水文站近6年(2016—2021年)的实际监测数据,为确保数据的准确性和完整性,首先对该水文站近6年的实际监测数据进行清洗、预处理,通过后向插值方法填充缺失数据,构建了黄河水沙流浪的时间序列数据集,数据信息表如表1所示。
1.2 含沙量与时间、水位、水流量的定性分析
对于水文站实际监测数据中的含沙量与时间、水位、水流量的定性分析,本文应用斯皮尔曼(Spearman)相关系数[5]对含沙量、时间、水位、水流量的关系进行定性分析,结果如图1所示。
由于斯皮尔曼相关系数评估的是两个连续变量之间的单调关系,通过斯皮尔曼相关系数可以对含沙量、时间、水位、水流量进行相关性分析,发现含沙量的变化与水流量,水位,时间都成正相关,且与水流量的相关度最强,与水位的相关度次之,含沙量与时间也有微弱的正相关性。
1.3 含沙量与时间、水位和水流量的定量分析
针对含沙量与时间、水位、水流量的具体大小变化趋势的关系,本文先以“newT(T)”“水位(Sw)”“水流量(Sl)”作为自变量,以“含沙量(Hsl)”作为因变量,通过多元线性回归分析方法[6]对含沙量与时间、水位、水流量进行了定量分析,并构建了其关系式为:
(1)
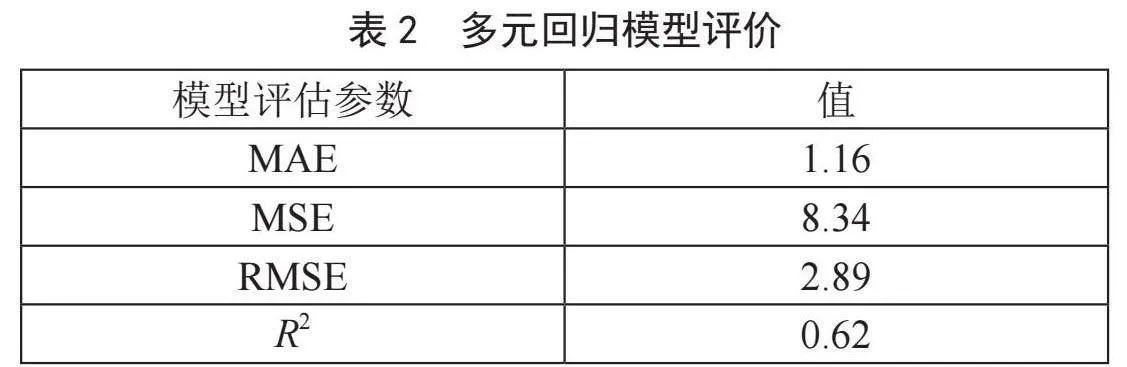
其中,C为拟合关系是常数项。根据数据集的拟合计算,分别得到其拟合系数和常数项的取值为:a=0.682 72,b=-0.004 58,c=0.000 6,C=-25.710 63。然后通过回归模型的性能指标,均方误差MSE,根均方误差RMSE,平均绝对误差MAE和拟合优度R2的评估分析,验证了本文所构建的含沙量与时间、水位、水流量的多元线性回归模型是可行的。评估如表2所示。
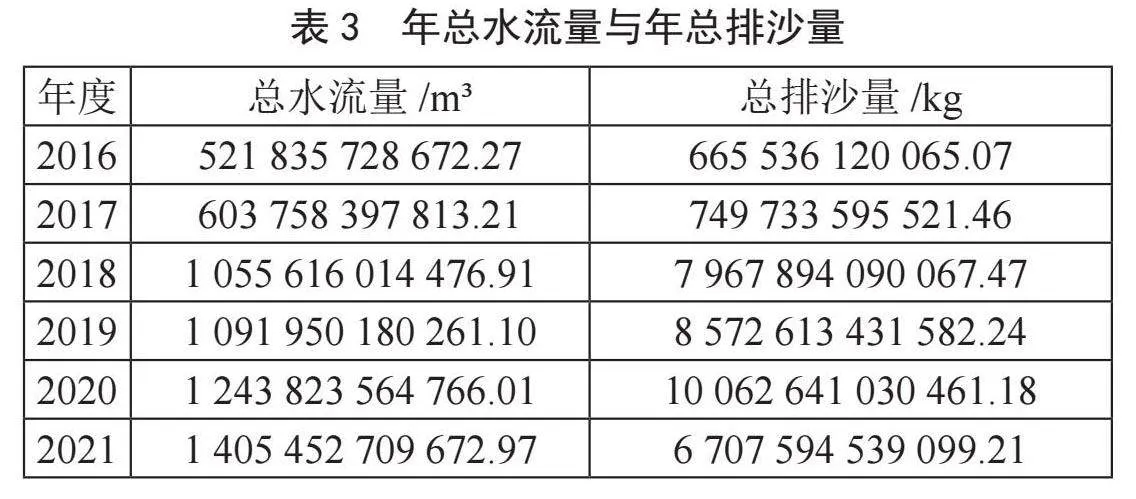
1.4 年总水流量和年总排沙量的估算
要估算该水文站近6年的年总水流量和年总排沙量,首先要计算出每一个检测时间点的排沙量(即:排沙量=水流量·含沙量),公式为:
(2)
然后,因为原始检测数据集中缺失值,填充后的数据集上各时刻点的监测数据仍然是离散型数值,要计算年总量,需以时间作为自变量,分别对水流量和排沙量做积分求和计算。最终得到每一年的年总水流量和年总排沙量。结果如表3所示。
1.5 水沙通量的变化规律分析
对近6年该水文站水沙通量的变化规律分析方面,本文从该水文站水沙通量在时间维度上的突变性,季节性和周期性变化规律进行了分析。
1.5.1 突变性分析
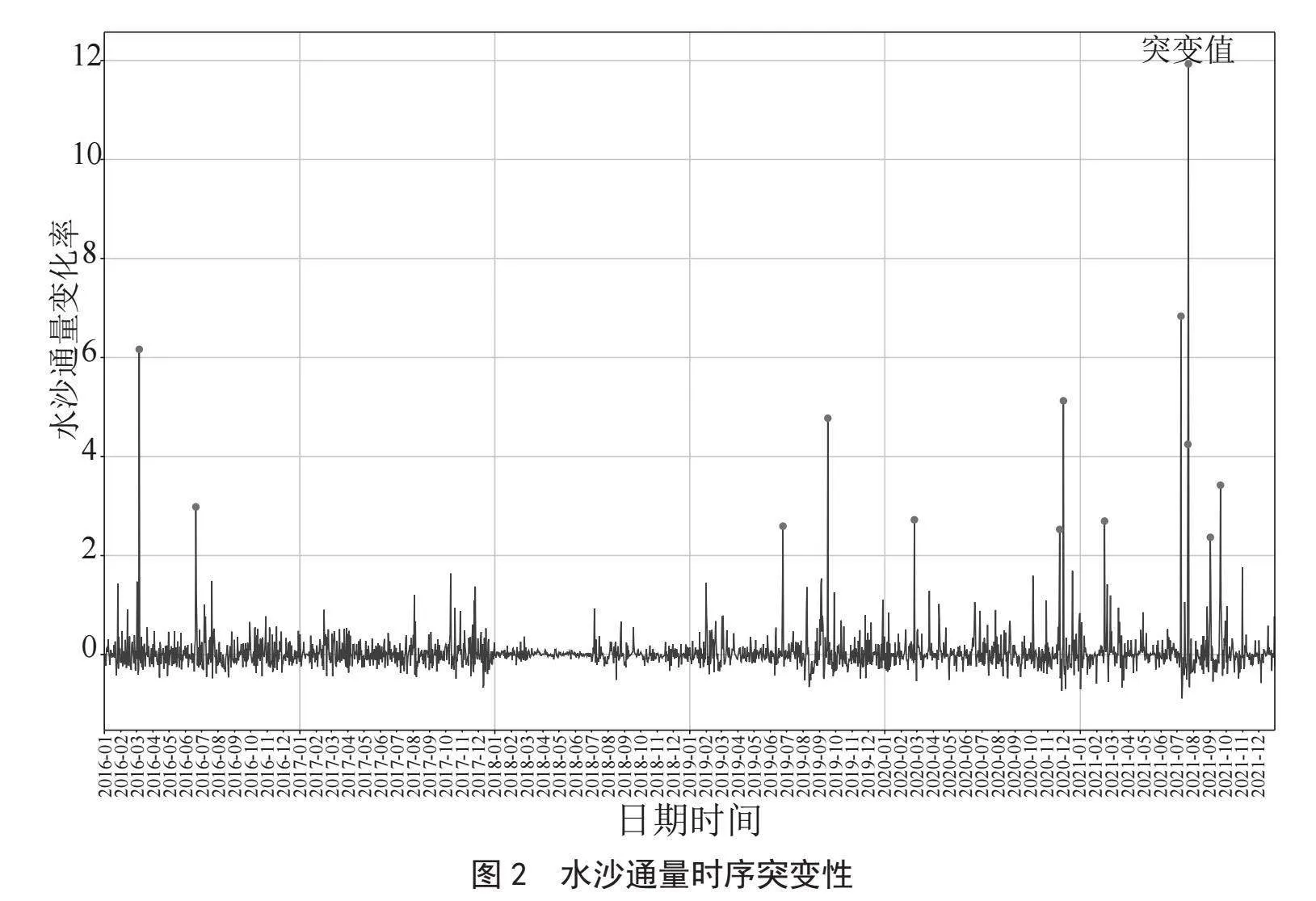
首先通过Python语言绘制水沙通量的时序图[7]对水沙通量近6年(72个月)内各时间点上的突变性进行了整体时序趋势分析,水沙通量时序突变性如图2所示。
通过对水沙通量时序图的观察发现,该水文站的水沙通量在2016年3月,2016年7月,2019年6556N0iQnlgBo+bsyU6y15w==月,2019年9月,2020年3月,2020年11月,2021年3月,2021年7月,2021年8月,2021年9月这些时间点上发生了明显的变化,特别是在2021年8月的水沙通量的突变性最为显著。
1.5.2 季节性分析
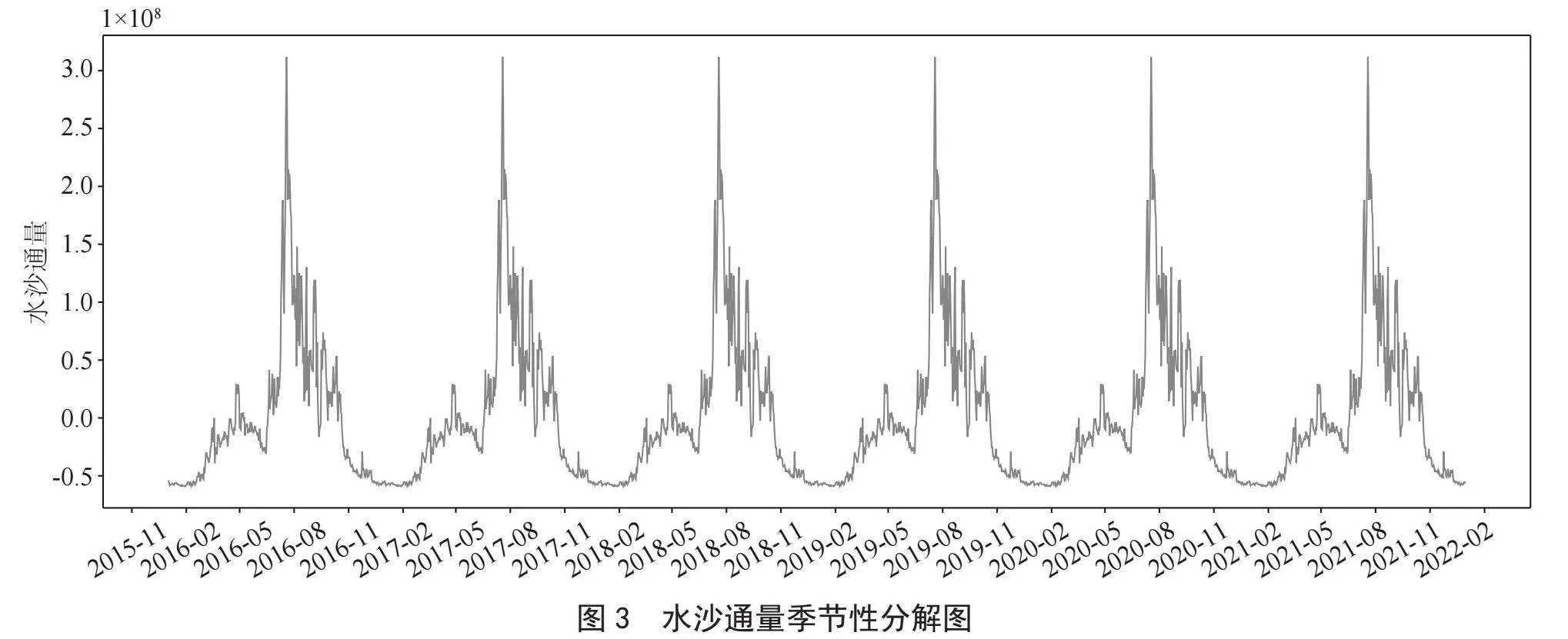
对于该水文站水沙通量的季节性变化规律,本文通过应用季节性分解的局部回归方法[8](STL)来分解水沙通量的时间序列数据,来观察并分析了该水文站的水沙通量的季节性变化趋势,如图3所示。
1.5.3 周期性分析
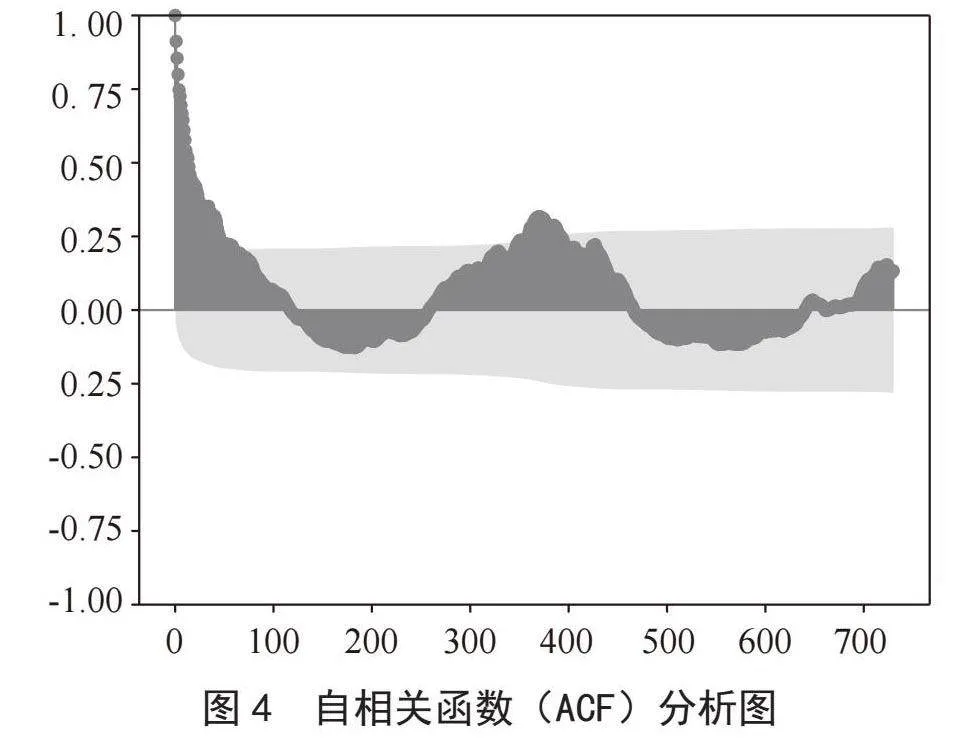
对于该水文站的水沙通量周期性变化的分析,本文应用变量自相关函数(ACF)分析方法[9]进行了分析,如图4所示。通过自相关函数(ACF)分析发现,该水文站的水沙通量与时间呈现极大的相关性,波峰与波谷的变化,极大值都很好的体现这种周期性,因此该水文站的水沙通量存在周期性变化趋势。
2 基于模型的黄河水沙监测数据分析
为了能及时掌握该水文站水沙通量的动态变化情况,又能最大限度地减少监测成本资源,本文基于时间序列算法SARIMA构建了一种对黄河水域未来两年的水沙通量进行预测的时间序列模型(SARIMAX),并通过平均绝对误差MAE、平均绝对误差百分比MAPE、均方误差MSE、根均方误差RMSE等指标对所构建的SARIMAX模型进行了性能评估分析。
2.1 构建SARIMAX模型
SARIMAX模型[10]是在差分移动自回归模型(ARIMA)的基础上加上季节(S)和外部因素(X)对时间序列数据进行分析的模型。其计算公式为:
(3)
其中,为非季节性自回归滞后多项式,捕获非季节性自回归元素。为非季节性自回归滞后多项式,捕获非季节性自回归元素。为时序数据d阶差分;季节性D阶差分:提供了时序平稳化功能。为季节性移动平均滞后多项式。
SARIMAX(p,d,q,s)模型意味着时序被差分了d次,且序列中的每个观测值都是用过去的p个观测值和q个残差的线性组合表示的。
SARIMAX模型构建步骤:
1)数据预处理。对原始数据集清洗,去噪,并对缺失值作插值处理。
2)序列平稳化。为了满足模型假设,检查序列的平稳性并执行相关转换。
3)确定差分d值。为了使序列平稳,将执行差分操作的次数确定为d值。
4)相关性分析(ACF,PACF)参数优化。网格搜索算法优化SARIMAX模型的参数。
5)确定p值和q值。从上一步的ACF和PACF图中读取p和q的值。
6)SARIMAX模型拟合。根据前面的参数值和计算结果,拟合SARIMAX模型。
7)模型验证与评估。在验证集上计算MAPE,通过分析MAPE值来检验模型的性能。
8)预测。以12个月为一个周期,预测未来两年(24个月)的值。
对于SARIMAX(p,d,q,s)模型的实现,本文通过设计Python程序,利用机器学习算法中的statsmodels库中的SARIMAX函数,对近6年该水文站的水沙通量的时间序列进行了训练,构建了水沙通量的时间序列模型SARIMAX模型。
2.2 模型参数优化与性能评估
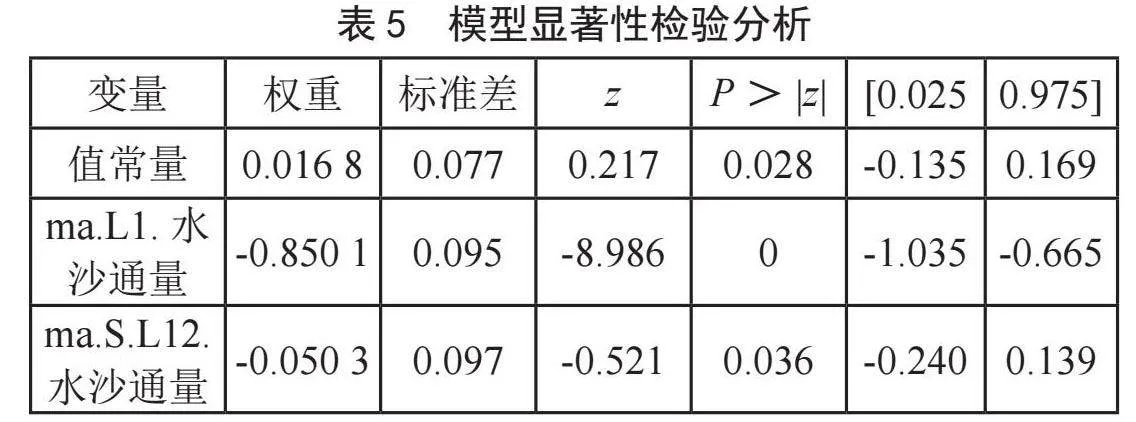
为提高SARIMAX模型的预测性能,本文对时序模型SARIMAX中的参数p,d,q,s进行了优化[11-12],通过网格搜索算法,对时序数据本身的滞后数p值和预测误差的滞后值q进行了搜索优化,最小的AIC值为780.24,对SARIMAX模型中的seasonal order参数网格搜索了最佳的季节性SARIMA的(p,d,q,s)值为(0,1,1,12),确定了分析该水沙通量的最佳的时间序列模型:SARIMAX(0,1,1,12)。所构建的SARIMAX模型相关参数及模型的显著性检验结果如表4、表5所示。
其中,权重列为每个变量的权重值;P>z列为对每个变量系数的检验。每个变量的P值均小于0.05,所以在0.05的显著性水平下,模型中每个变量的系数通过显著性检验。将模型SARIMAX(0,1,1,12)在验证集上进一步验证分析,发现模型的平均绝对百分比误差(MAPE)降到17.4%,即准确率达到了82.6%。所以此模型对水沙通量值的预测是可行并有效的。
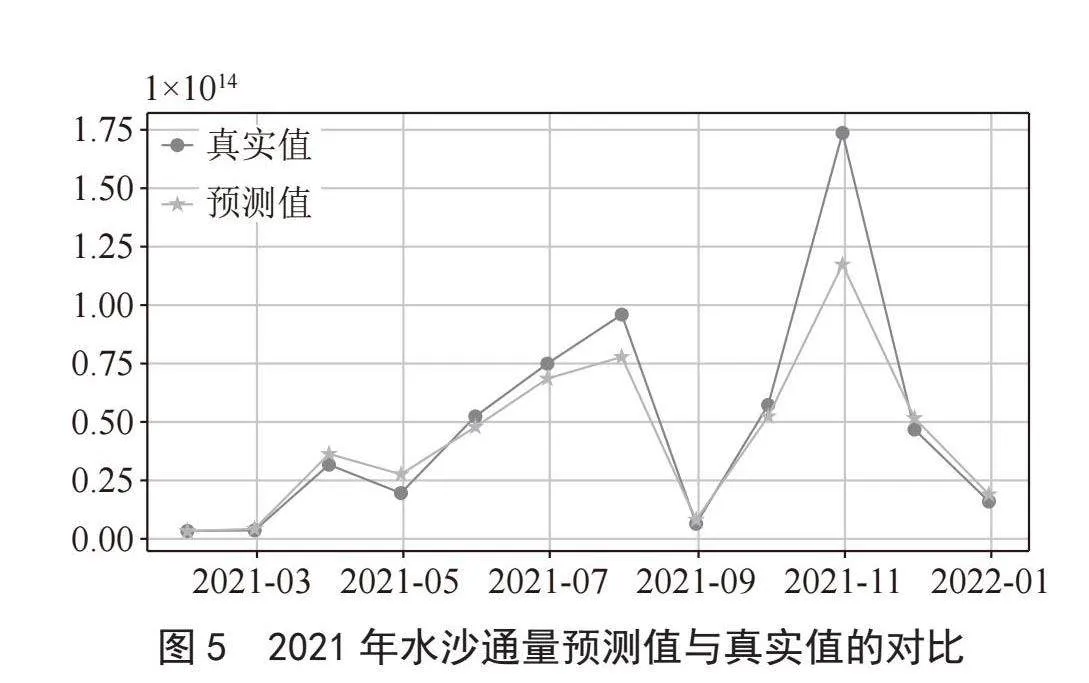
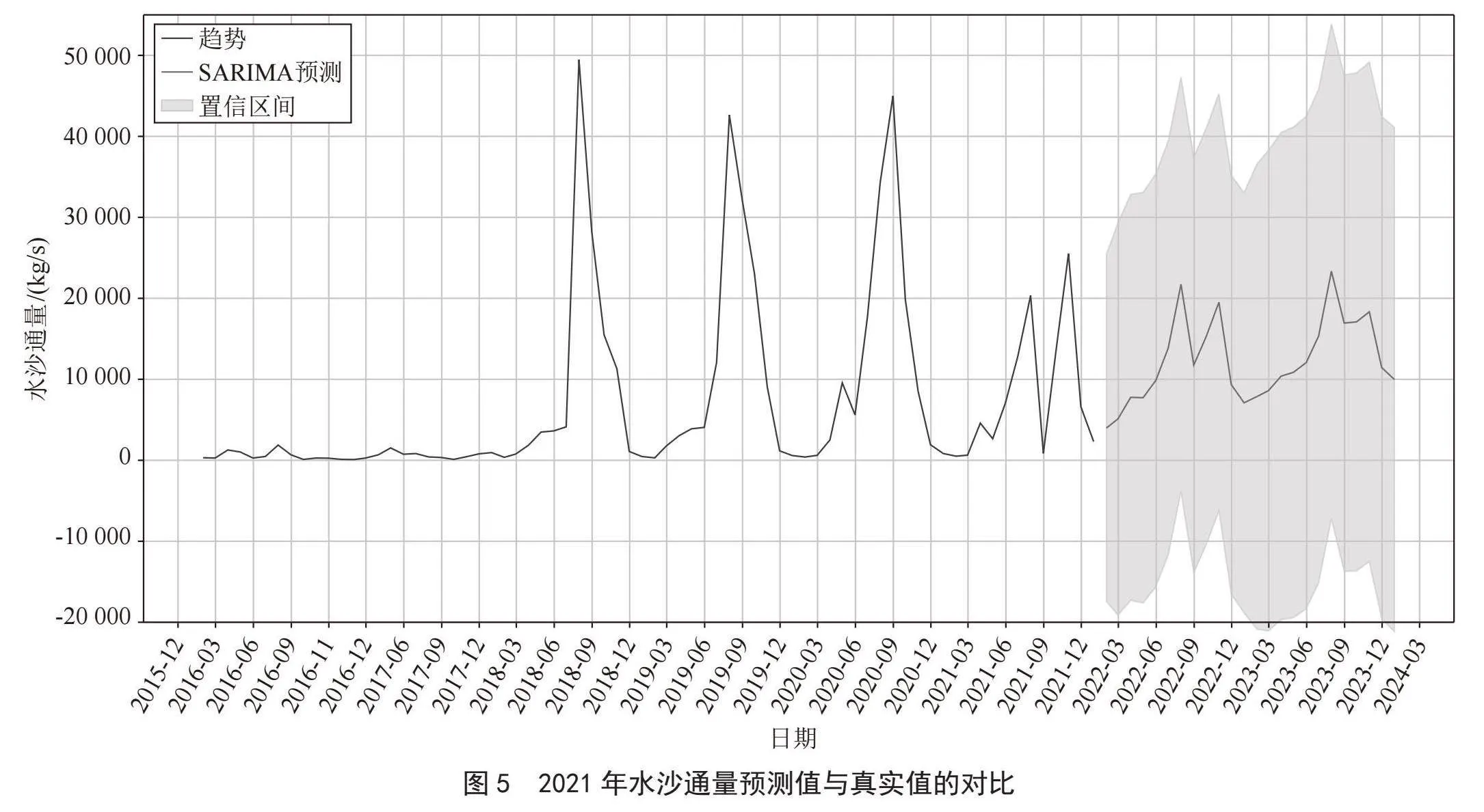
为了进一步评估SARIMAX(0,1,1,12)模型的性能,本文在原始数据集中2016—2021年间的水沙通量对模型进行验证性分析:首先以2016—2020年的水沙通量监测数据训练模型,预测2021年12个月的水沙通量情况,然后,通过对2021年实际的水沙通量监测数据和模型预测值进行比较分析如图5所示;发现SARIMAX(0,1,1,12)模型的拟合优度R2为0.89,此时的平均绝对百分比误差(MAPE)降到18.12%得出,该模型对黄河水文站的水沙通量的预测具有较高的准确性。
3 SARIMAX模型预测未来两年的水沙通量
通过前面确定的最优模型SARIMAX(0,1,1,12),本文以该水文站2016—2021年间水沙监测数据作为训练集,对SARIMAX(0,1,1,12)模型进行训练,然后以该水文站2022—2024年未知的水沙通量作为预oGhNX/5Pa4DC8oq4wluNL0sG0hTnBOBPiFyOwKJRbGQ=测值,设置SARIMAX模型的预测位移量(steps)值为24,即对2022—2024年24个月内的水沙通量数据进行预测,预测结果如图6所示。
从图5中2022—2024年两年内的水沙通量预测结果可以发现,本文所构建的SARIMAX(0,1,1,12)模型预测的水沙通量值均落在了置信区间[0.025,0.975]内,说明该预测结果是具有较高的可信度。综上分析研究得出,该模型的预测值对优化黄河流域水资源分配、协调人地关系、调水调沙、防洪减灾等方面都具有实质的理论指导意义。
4 结 论
本文通过分析黄河某水文站2016—2021年间的水位、水流量与含沙量的实际监测数据,研究了该水文站水沙通量的变化规律及其周期特性;由此应用了机器学习算法中的时间序列分析算法构建了一种对黄河水文站的水沙通量变化的预测模型SARIMAX(0,1,1,12)。通过对该模型的参数优化和显著性检验分析,得出该模型对黄河水沙通量的变化趋势的预测具有较高的准确性,其预测结果可为黄河水文环境的保护和黄河水域“调沙调水”等工作提供准确的参考依据。
参考文献:
[1] 褚言皓,吴文娟,李鹏,等.黄河口悬浮泥沙时空动态及其驱动机制 [J].海洋学报,2022,44(6):150-163.
[2] 王俊杰,拾兵,巴彦斌.近70年黄河入海水沙通量演变特征 [J].水土保持研究,2020,27(3):57-62+69.
[3] 刘明,杨雅迪,毕乃双,等.2015年调水调沙期间黄河悬浮颗粒Pb及其稳定同位素组成变化 [J].中国环境科学,2019,39(7):3009-3017.
[4] 全国大学生数学建模竞赛组委会.2023全国大学生数学建模E题[EB/OL].[2023-09-26].https://www.mcm.edu.cn.
[5] 魏光琼.级相关在综合评估法评标中的应用 [J].工程建设与设计,2014(9):156-160.
[6] 肖晓华,胡依,李贝.基于多元线性回归的高校大学生专业认同现状及影响因素研究[J].中国高等医学教育,2020(3):26-27.
[7] 彭维湘.时间序列中DF单位根检验存在的问题及方法改进 [J].统计与决策,2022,38(21):53-56.
[8] 宋长鸣,徐娟,项朝阳.基于时间序列分解视角的蔬菜价格波动原因探析 [J].统计与决策,2014(3):106-108.
[9] 蒋水华,李典庆,周创兵,等.考虑自相关函数影响的边坡可靠度分析 [J].岩土工程学报,2014,36(3):508-518.
[10] 周鑫,李燕,曾永辉,等.基于SARIMAX-SVR的光伏发电功率预测 [J].电力系统及其自动化学报,2024,36(5):1-8.
[11] 李国栋,周扬,李凯.基于SARIMAX-XGBoost模型的区域能耗预测 [J].电力信息与通信技术,2022,20(3):26-33.
[12] 邹银先,褚学伟,段先前,等.不同时间序列模型在岩溶山区矿井涌水量预测中的应用 [J].中国岩溶,2023,42(6):1237-1246.
作者简介:李长生(1990.08—),男,汉族,甘肃武威人,讲师,硕士,研究方向:数据挖掘、数据可视化。