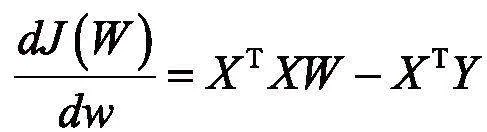
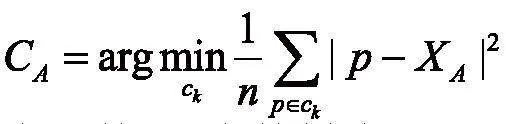

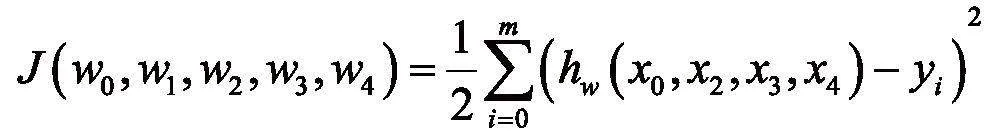

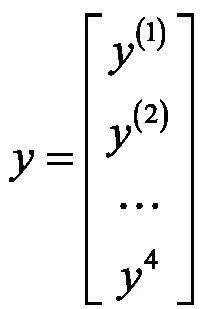
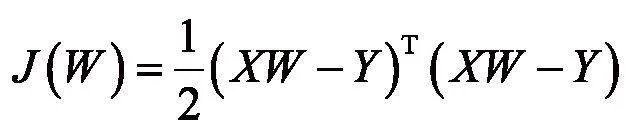
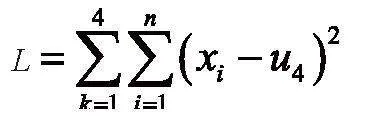

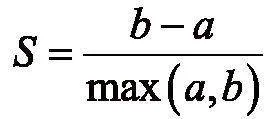

摘" 要:随着信息技术的发展,各类数据管理与数据分析技术广泛应用,为社会高质量生活带来诸多便利。在深入研究数据库技术及数据分析技术的基础上,设计了一种对学生体能训练任务智能规划系统。该系统通过设计六个核心表,实现了对人员数据的全面管理,提供了增、删、改、查等基本数据管理功能。同时,该系统还实现了智能化人员分组与成绩预测的功能,其不仅可以采用预设的判断语言进行初步分组,还引入K-means算法进行智能分组,确保了分组的科学性和准确性。此外,智能系统利用线性回归和随机森林模型进行成绩预测,为教练团队制定训练计划提供了更加科学和精准的决策参考,并对学生体能成绩的快速提高提供有效支撑。
关键词:SQL Server数据库;K-means算法;线性回归模型预测;随机森林模型预测
中图分类号:TP" " " 文献标识码:A" " " 文章编号:2096-4706(2023)22-0074-07
Design and Implementation of Intelligent Planning System for Students Physical Training Tasks
Abstract: With the development of information technology, various data management and data analysis technologies are widely used, bringing many conveniences to high-quality social life. Based on the deep research on database technology and data analysis technology, an intelligent planning system for students physical training tasks is designed. This system achieves comprehensive management of personnel data through the design of six core tables, and provides basic data management functions such as adding, deleting, modifying, and querying. At the same time, this system also realizes the functions of intelligent personnel grouping and performance prediction. It not only uses preset judgment language for preliminary grouping, but also introduces the K-means algorithm for intelligent grouping, ensuring the scientificity and accuracy of grouping. In addition, the intelligent system uses Linear Regression and Random Forest models for performance prediction, provides more scientific and accurate decision-making references for the coaching team to formulate training plans, and provides effective support for the rapid improvement of students physical performance.
Keywords: SQL Server database; K-means algorithm; Linear Regression model prediction; Random Forest model prediction
0" 引" 言
随着信息技术的发展,各类数据管理与数据分析技术广泛应用,给人们的生产生活带来诸多便利。体能训练作为学生身心健康发展的关键环节,对于塑造强健的体魄、培养坚韧的意志品质具有不可替代的作用。然而,面对学生群体的多样化特点,如何制定科学、有效的训练计划,成为教育工作者和体育教练们面临的一大难题。传统的体能训练方式往往依赖于教练的经验和直觉,缺乏精准的数据支持和个性化的指导。这不仅影响了训练的效果,还可能增加学生受伤的风险。此外,学生个体的生理条件、伤病状况以及训练环境、场地设备等外部因素,都为体能训练带来了更多的不确定性。如何在充分考虑这些因素的基础上,制定出更加科学、合理的训练计划并对学生的成绩进行合理预测、调整方案,确保学生在安全的前提下取得最佳的训练效果,成为迫切需要解决的问题。
因此,本文旨在依托数据管理与分析技术,采用SQL Server数据库、Python语言实现对数据的管理,采用K-means聚类算法、线性回归和随机森林模型实现对数据的分析挖掘,设计并实现了一种体能训练任务智能规划系统。该系统全面分析了学生的工作安排、个人特点、硬件设施以及训练规律,为教练团队提供科学、精准的训练计划建议,并预测训练成绩。通过这一系统的应用,我们希望能够解决当前体能训练中教练团队制定方案不科学、不合理的问题,以提升训练效果为核心目标,确保学生的安全与健康,从而为学生的全面发展奠定坚实的基础。
1" 系统设计架构
1.1" 研究思路、框架与主要内容
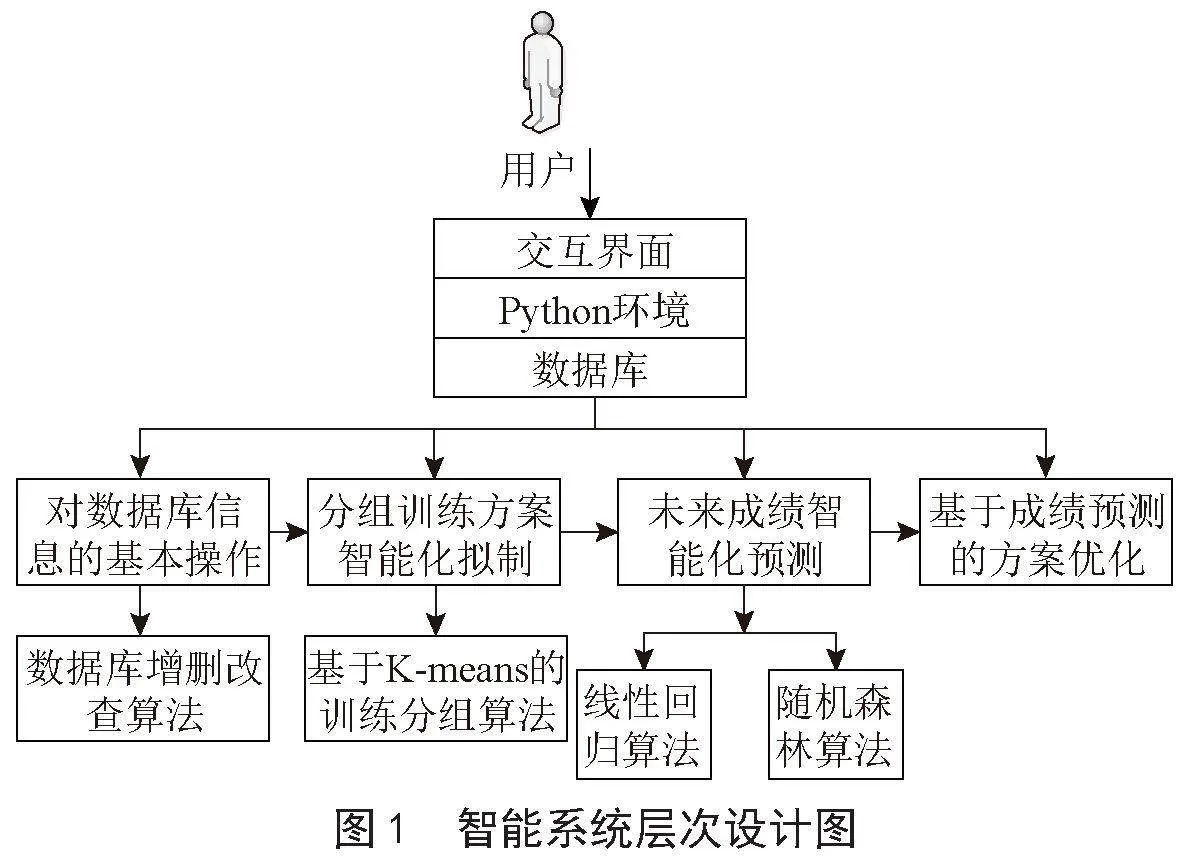
该系统的设计思路是按照SQL Server数据库设计、查询系统设计、方案系统设计、预测系统设计、界面设计与优化来进行的,如图1所示。
具体设计如下:
1)数据库构建与数据填充。系统利用SQL Server数据库软件精心构建了六个核心表:人员情况表、人员成绩表、天气情况表、场地占用表、物资占用表和工作安排表。并填入相关数据,为后续分析决策提供坚实支撑。
2)Python与SQL Server的交互。为实现与数据库的灵活交互,选用Python语言和PyCharm编辑器实现系统的增、删、改、查功能[1]。这些功能提供直观易用的操作界面,满足用户访问和修改数据的需求[2],如图2、图3所示。
3)智能人员分组及方案设计。系统依据人员薄弱科目初步分组,再借助K-means算法智能深化分组,为管理者决策提供依据。同时支持手动调整分组,满足实际管理需求。
4)成绩预测模型与运用。为了实现对人员成绩的预测,初步选择线性回归模型预测人员成绩,而后引入随机森林模型提高预测精度与智能化水平。通过集成多个决策树,实现更精细化预测,为管理者决策提供更准确参考。
1.2" 数据库设计
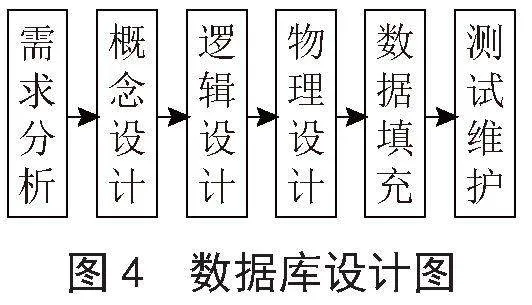
本智能系统数据库构建至关重要,数据库负责组织、存储、管理数据,确保数据的完整性、安全性、一致性,支持高效的检索和分析[3]。本节将详细解析设计流程,包括需求分析数据类型及关系,概念设计用实体-关系图展示实体关联,逻辑设计定义表结构,含字段、数据类型,具体步骤如图4所示。
1.2.1" 需求分析
旨在明确记录和管理学生信息、成绩、天气、场地、物资及工作安排的综合需求。在数据需求方面,为确保数据一致性与处理灵活性,要求所有数据以字符型存储。其中,学生信息管理需涵盖姓名、年龄、性别等基础数据,以及伤病、训练历史、体能等详细信息,为教练团队个性化训练提供依据。成绩记录包括各项体能测试成绩,用以评估训练效果和调整计划。天气、场地和物资数据助力教练团队合理安排训练,规避不良影响。同时,工作安排需明确每日计划、人员分配及物资需求,确保训练高效有序。
1.2.2" 概念设计
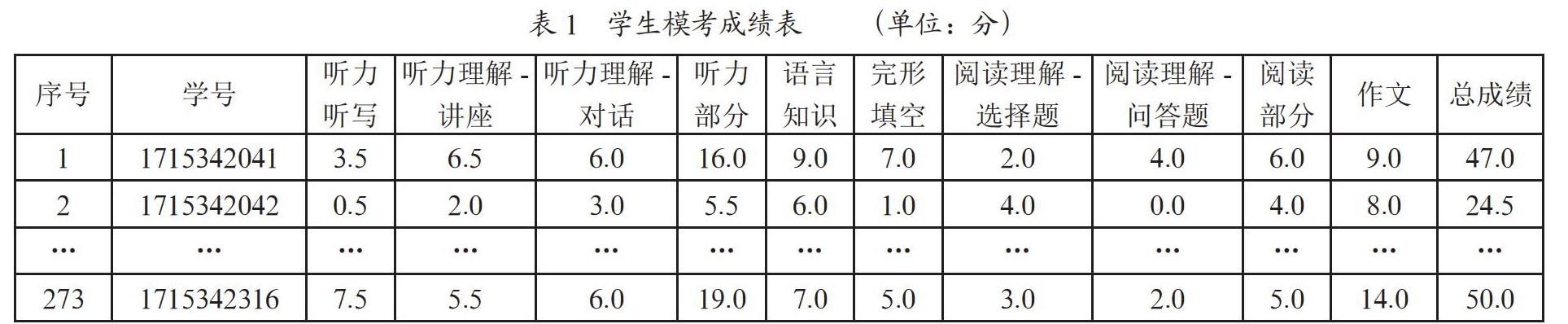
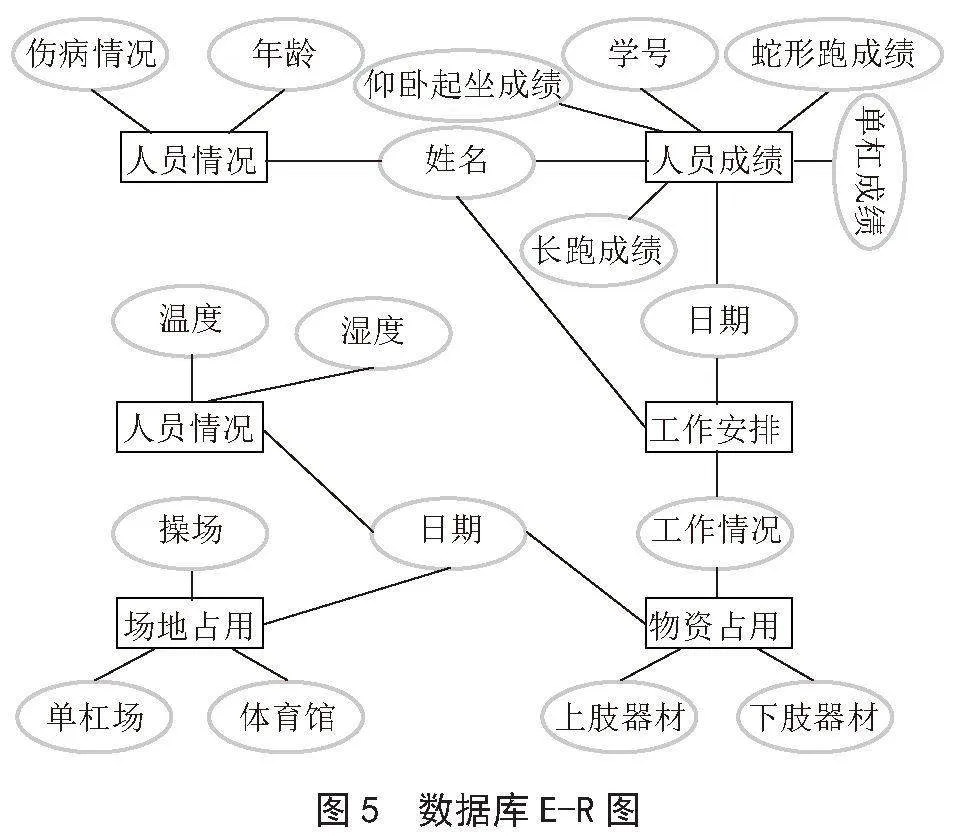
概念设计是数据库设计的关键阶段,它涉及将用户需求抽象为不依赖于特定数据库管理系统的概念模型。在本设计中,将使用实体-关系(E-R)模型来表示数据库中的各个实体及其关系,如图5和表1所示。
1.2.3" 逻辑设计
逻辑分析是数据库设计过程中的一个关键阶段,它涉及将概念设计转化为数据库管理系统能够理解的逻辑结构。在这一阶段,将根据概念模型进一步定义数据库的逻辑结构。
根据概念设计可以确定表之间的关系。虽然数据类型都被设计为char型,但在逻辑分析阶段,系统设计时需要确定哪些字段更适合作为数值型,以提高查询效率和存储空间。
2" 训练方案智能生成功能
随着大数据和人工智能技术的飞速进步,在人员分组与方案设计领域,传统的基于经验和直觉的方法已经难以满足现代管理和培训的需求。因此,本文提出“智能人员分组与方案设计”新方法,引入智能化策略,实现更科学、高效、灵活的人员分组与方案设计。系统首先基于学生薄弱科目自动分组,而后引入K-means算法进行更精准的人员分组,并注重教练团队的决策权,允许手动调整分组。
2.1" 补差分组
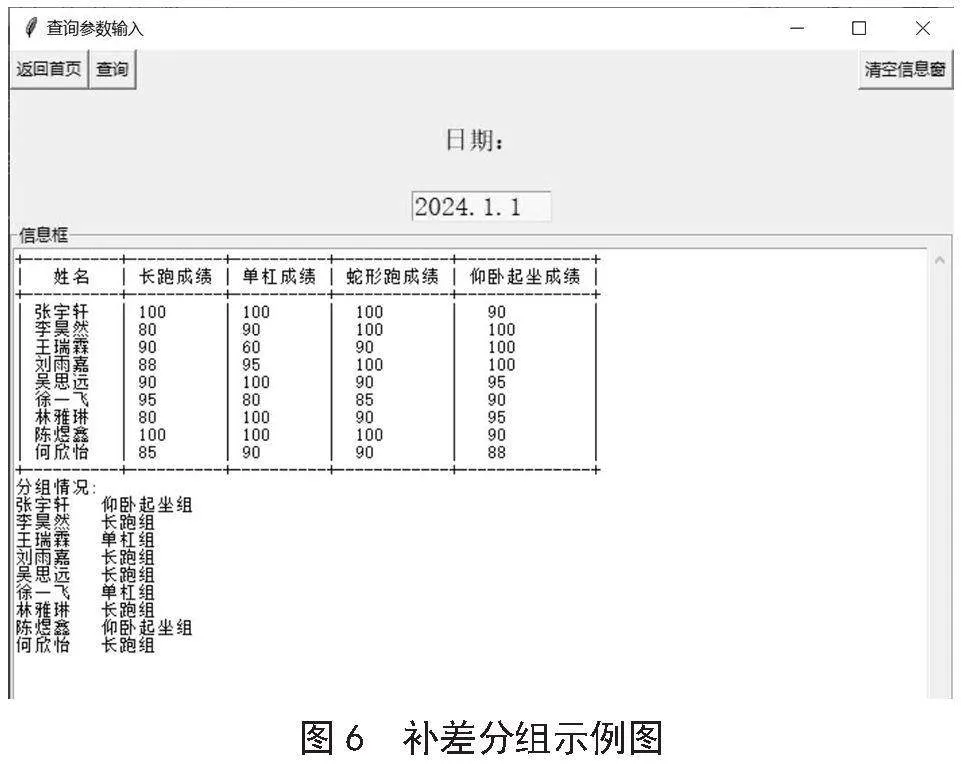
智能化系统通过Python库连接SQL Server,检索人员成绩数据并遍历每行数据,利用条件语句和MIN函数找出每个人四门科目的最低成绩,依据最弱科目成绩分组提供针对性指导。最终将分组结果展示于图形界面并保存至数据库,支持后续科学方案生成,界面如图6所示。该算法初步实现了智能化分组,提升了训练管理效率,并为学生提供科学、高效训练方法。
2.2" 综合分组
上述补差算法注重将相同薄弱科目的人员分为一组,并提出有针对性的训练方案并进行强化训练。但是该方法适合在有较强针对性的前提下实行,在此基础上系统引入K-means算法,提高了人员分组的科学化、智能化,为教练团队对所属人员体能训练水平的整体掌握和管理提供有力支撑。
2.2.1" 基于K-means算法的人员训练分组算法
在K-means算法中,通常使用肘部法则(Elbow Method)来确定k值,以最小化样本与质点平方误差作为目标函数,将每个簇的质点与簇内样本点的平方距离误差和称为畸变程度,对于一个簇,其畸变程度越低,代表簇内成员越紧密,畸变程度越高,则代表簇内结构越松散[4]。在本系统中,选定k值为4。
本系统中K-means算法用距离作为相似性指标[5],从而发现给定数据集中4个类,且每个类的中心是根据类中所有值的均值得到的,并由每个聚类中心来描述。对于给定的一个包含n个6维数据点的人员成绩数据集x,以及分得的4个类别,选取欧式距离作为相似度指标,聚类目标是使得各类的距离平方和最小,即最小化:
结合最小二乘法和拉格朗日原理,聚类中心为对应的平均值。同时,为了确保算法收敛,在迭代过程中,应使最终的聚类中心尽可能稳定不变。
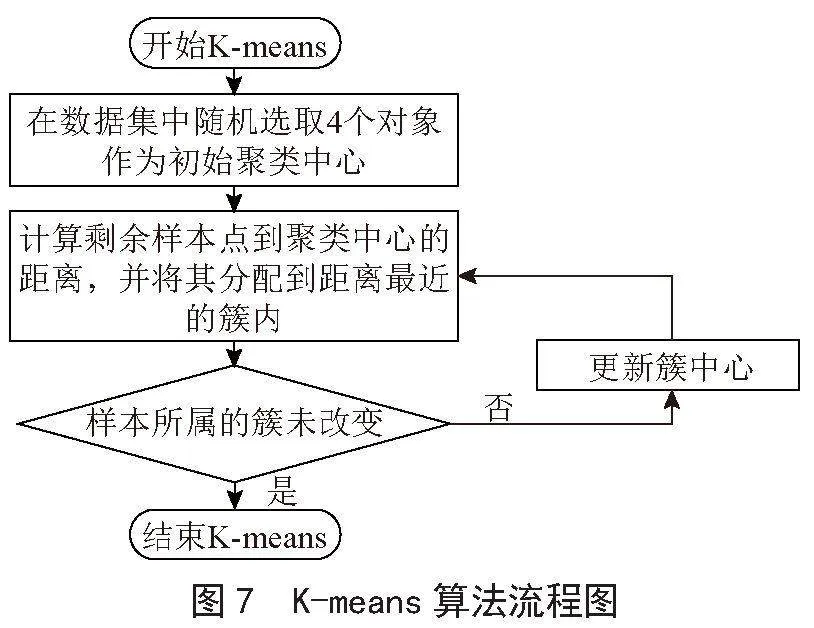
如图7所示,本算法的流程分为以下4个步骤:
1)选取数据空间中的4个对象作为初始中心,每个对象代表一个聚类中心。
2)对样本中的数据对象,根据其与这些聚类中心的欧式距离,按距离最近的准则将其分到距离最近的聚类中心所对应的类。
3)更新聚类中心,将每个类别中所有对象所对应的均值作为该类别的聚类中心,计算目标函数的值。
4)判断聚类中心和目标函数的值是否发生改变,若不变则输出结果,若改变,则返回步骤2)。
轮廓系数是类的密集与分散程度的评价指标,针对该指标,在聚类任务中,希望得到簇内尽量紧密、簇间尽量远离的结果,学生A的样本点XA的轮廓系数表达如下:
其中,a表示学生A成绩的样本点XA与同簇的其他学生样本的平均距离,称为凝聚度,b表示XA与最近簇中所有样本的平均距离,称为分离度。而最近簇为:
其中,p表示簇CA中的样本,即用学生A成绩样本XA到相关簇所有样本平均距离作为衡量该点到该簇的距离后,选择离样本点XA最近簇作为最近簇。
而后利用Calinski-Harabasz准则确定聚类评价指示:
分离度越大。
2.2.2" K-means智能分组示例
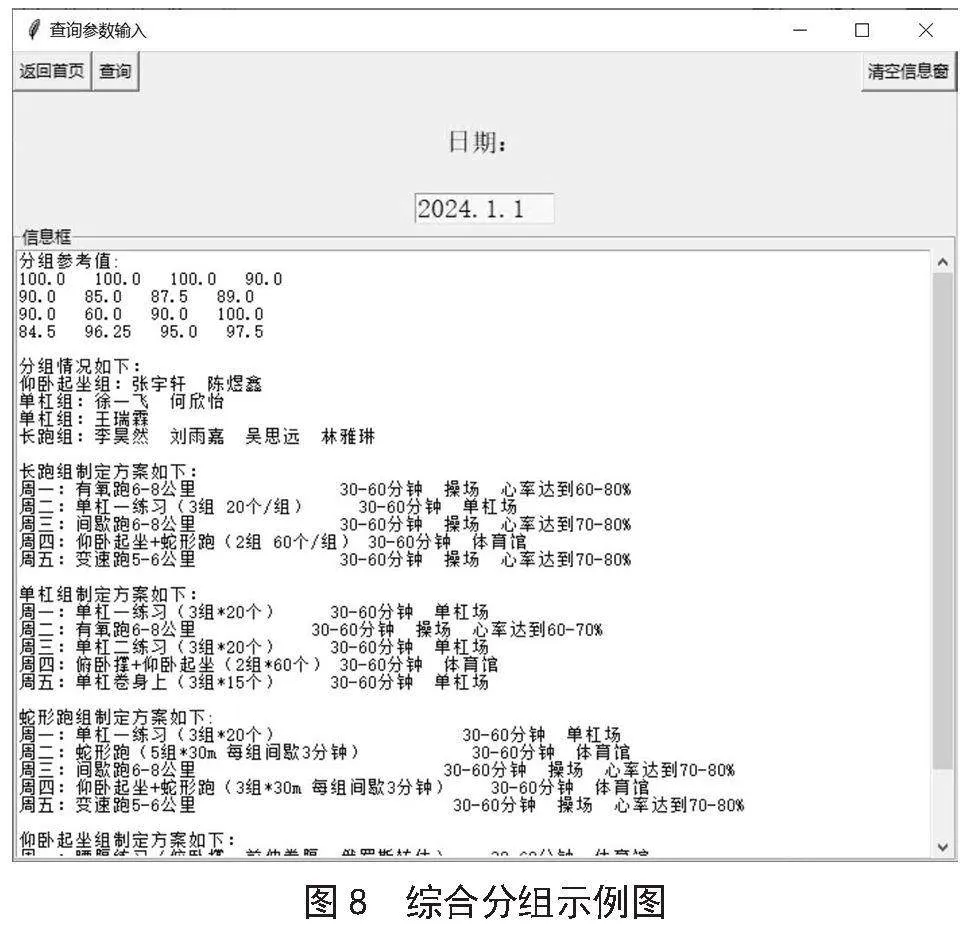
用户通过界面输入日期后,系统筛选该时间段内的人员成绩数据,并经过K-means聚类算法处理完成绩相近度分组。其中,每组的聚类中心通过比较确定最弱科目作为组别名称,为每个组别生成定制化训练方案,界面展示如图8所示。另外,教练团队可通过系统展示的聚类中心直观了解分组情况,快速把握各组的整体成绩水平和特点。此系统不仅提高了分组效率和准确性,还为教练团队提供了有价值的参考,助力他们更有效地制定训练计划,促进人员成绩提升。
3" 智能成绩预测
本部分聚焦于线性回归和随机森林模型在学生体能训练成绩预测中的应用。系统先利用了线性回归模型对四门成绩进行初步预测,该方法虽简单易行,但受限于其线性假设,难以应对复杂关系和高维特征。为提升预测精度,系统进而采用随机森林模型,通过集成多个决策树,捕捉复杂关系并增强泛化能力。随后,对比分析两种模型的预测结果,以展现随机森林模型在精确性和适用性上的优势。通过这种方式,教练团队得以更有效地掌握学生体能训练水平,制定个性化训练计划,推动学生成绩提升。
3.1" 基于线性回归的成绩预测模型
3.1.1" 理论方法
线性回归模型是基于数理统计原理,用于确定两种及以上变量之间相互依赖的定量关系的回归分析。其核心假设是变量间的关系呈线性,即通过直线或超平面来拟合变量之间的关系[6]。本系统中模型定义为:
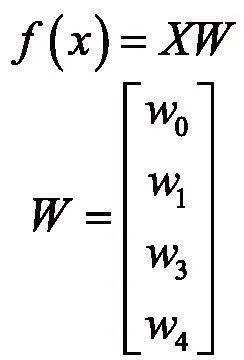
使用矩阵表示为:
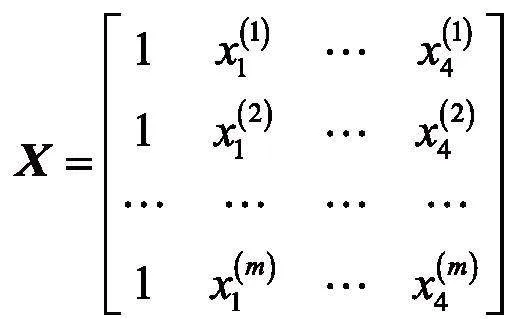
其中,W表示要求的一系列成绩预测参数,X表示学生A成绩的m次体能考核成绩样本集,用矩阵表示如下:
考虑常数项W0,因此在矩阵第一列加上了1, 代表学生A第一次的体能考核成绩, 代表A学生第m次体能考核成绩。4项体能成绩预测值为:
另外,为有效衡量并处理误差,系统使用均方误差作为损失函数,表达如下:
矩阵写法为:
利用最小二乘法[7]得:
令导函数为零,解得预测参数为:
3.1.2" 具体实现
线性回归模型依系统具体实现步骤如下:
1)数据准备。通过Pymssql库连接“训练”数据库,检索用户“吴思远”的历史成绩数据,涵盖长跑、单杠等科目及测试日期“2014.1.4”。利用Pandas处理数据,将日期格式化为datetime类型,即“year=2014,month=1,day=4”,并转换为自最早日期2024.1.1起的天数,形成结构化数据集。进而计算日期差值作为新特征“天数”,为后续的线性回归模型训练提供支持。
2)特征和目标选择。本步骤选择了“天数”作为特征,在本例中天数为3,它代表了自最早日期2024年1月1日以来的时间流逝。该特征的选择基于一个假设,即时间因素可能对“吴思远”的成绩产生影响。同时,系统确定了多个目标变量,包括“长跑成绩”“单杠成绩”“蛇形跑成绩”和“仰卧起坐成绩”,这些目标代表了不同方面的体能表现。
3)模型训练。通过数据准备与特征选择后,形成含相关特征和目标变量的数据集。为评估模型泛化能力并防止过拟合,使用train_test_split函数将上述“吴思远”的数据集随机拆分为80%训练集和20%测试集。利用训练集特征和目标数据,并通过最小二乘法训练线性回归模型,以最小化预测误差,逼近最优解。
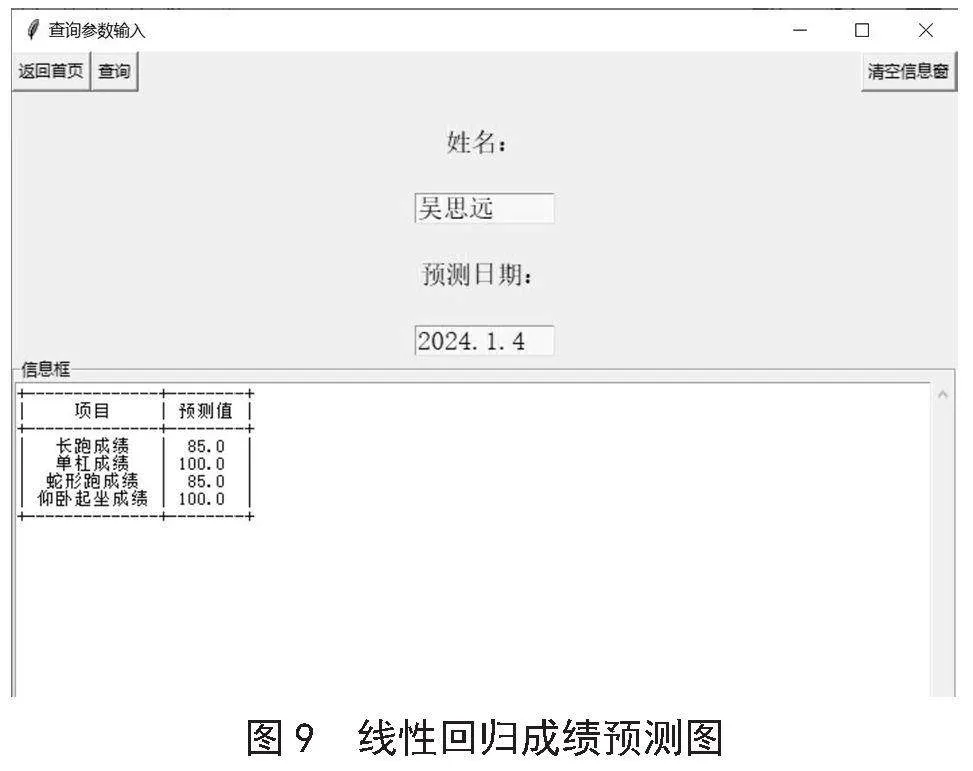
4)预测结果。完成数据准备、特征选择、数据拆分和模型训练后,得到训练好的线性回归模型。该模型通过学习训练集数据的规律,建立了特征与目标之间的线性关系。在预测阶段,系统利用该模型对连队管理者所输入的3天天数差进行计算,输出预测值依次为“85,100,85,100”。为确保预测值的合理性,系统对结果裁剪处理,以保证学生成绩在0到100的范围内。本例中,裁剪结果不变,即“85,100,85,100”。预测结果界面如图9所示。
3.2" 基于随机森林的成绩预测模型
3.2.1" 理论方法
依据系统实现随机森林算法如下:
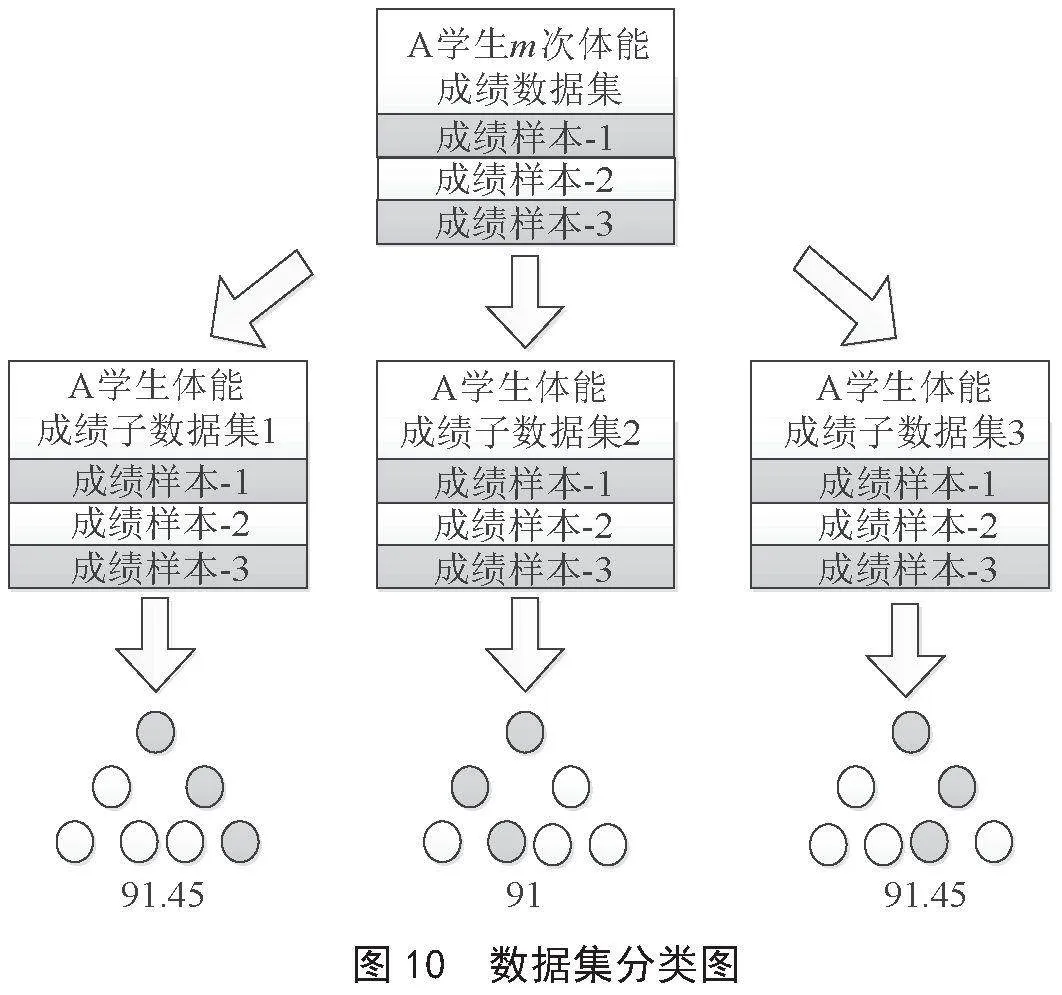
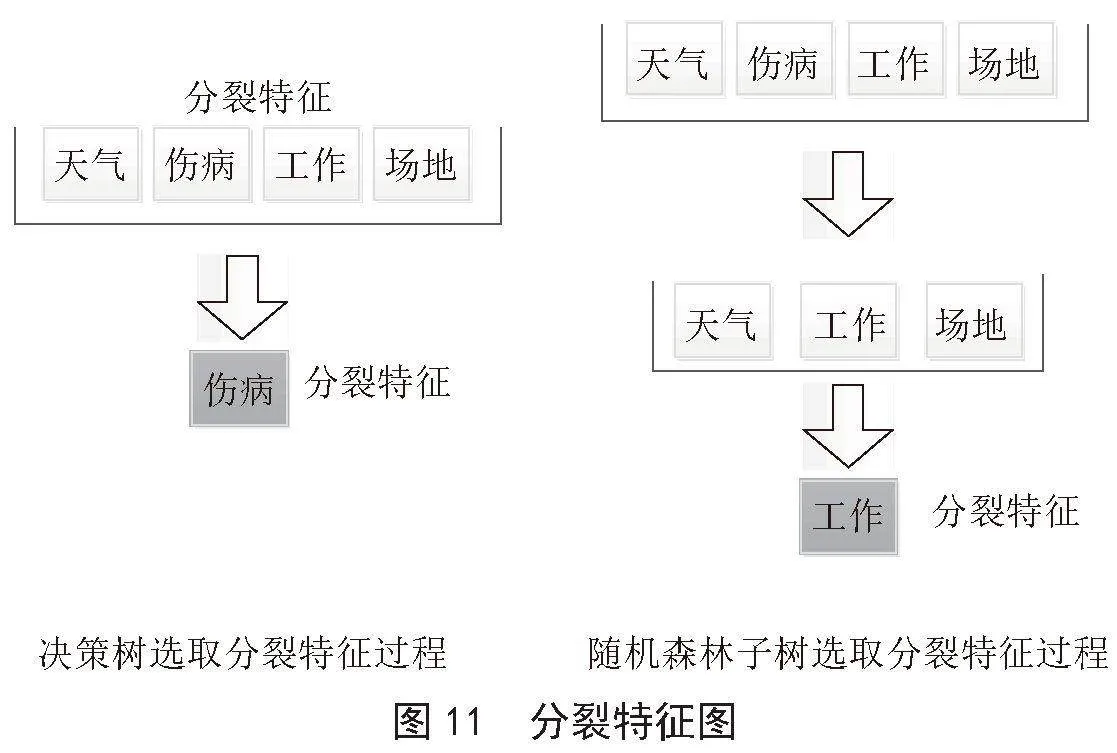
1)数据的随机选取。随机森林算法通过有放回抽样构造多个子数据集,并用于独立构建子决策树[8]。新数据输入时,每棵子树输出预测结果,通过聚合相应的结果(如投票或平均)得到随机森林的最终输出,从而提高模型的稳定性和泛化能力。如图10所示,假设学生A体能成绩数据集所构成的随机森林中有3棵子决策树,其中2棵子树的决策结果为91.45分,1棵子树的决策结果为91分,那么随机森林的决策结果则为91.45分。
3.2.2" 具体实现
随机森林模型依系统具体实现步骤如下:
1)数据准备。连队管理者输入“吴思远”,而后系统依据上述姓名访问数据库录入的成绩记录,包括日期、长跑、单杠、蛇形跑和仰卧起坐成绩等并将成绩字段转为Pandas DataFrame,将日期字段转换为datetime类型,本例中相关字段为“year=2014,month=1,day=4”。预处理阶段,系统新增“天数”特征,计算最早记录日期“2024.1.1”到用户输入日期“2024.1.4”的天数差,以捕捉时间因素对成绩的影响。
2)模型训练。系统利用随机森林回归算法构建预测模型,通过train_predict_model函数,以DataFrame、特征列名“天数差”和目标列名“长跑、单杠、蛇形跑、仰卧起坐”作为参数进行训练并返回模型。在train_models函数中,针对每个目标成绩分别调用train_predict_model函数进行独立训练,并以“天数”为特征预测目标成绩,其中本例中天数为3。
3)随机森林构建。系统利用集成学习的方法创建多个决策树模型,并将其组合成随机森林回归器。通过RandomForestRegressor实例化模型,并设置100棵决策树。在训练过程中,每棵树随机选择特征和样本进行拟合,以增加模型的多样性和减少过拟合的风险。random_state=42的设置确保了模型构建的随机性一致,从而使实验结果可复现。
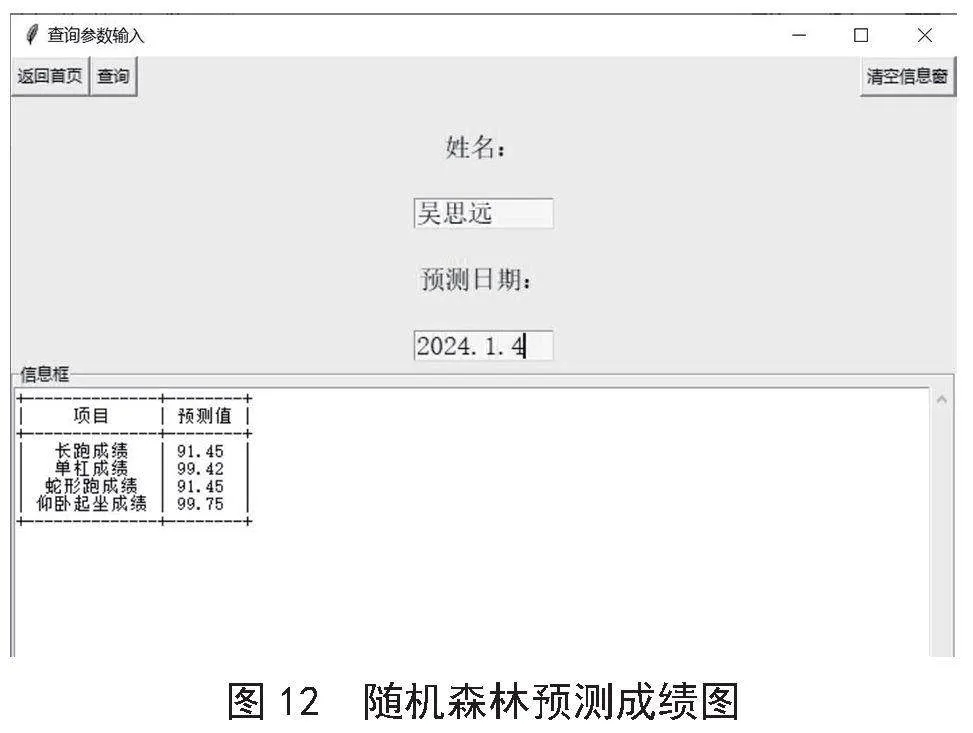
4)预测结果。用户通过输入预测日期“2024.1.4”,系统根据相关数据计算天数差并作为输入特征。而后,已训练的随机森林模型基于时间与成绩关系,对目标成绩进行预测,本例中吴思远成绩的预测值为“91.45,99.42,91.45,99.75”。另外,系统使用np.clip函数对预测值裁剪以确保其在0到100分的合理范围,本例中裁剪结果不变,即“91.45,99.42,91.45,99.75”。预测结果界面如图12所示。
4" 结" 论
本文详细阐述了智能化任务系统在体育训练领域的应用,展现了其强大的数据处理与展示能力。通过SQL Server数据库与Python的紧密集成,该系统实现了对学生体能训练数据的深度挖掘和高效处理。借助直观的可视化界面,教练团队能够直观地查看和分析学生的体能数据,从而更全面地掌握学生的训练情况。在训练方案制定方面,系统采用了先进的K-means算法,通过对学生的体能数据进行聚类分析,能够精准地将具有相似体能特点的学生划分到同一组中。此外,系统还结合了线性回归和随机森林算法,对学生成绩进行了有效的预测,通过对历史成绩和体能数据的综合分析,预测出学生在未来一段时间内的成绩变化趋势,同时为辅助教练团队制定科学合理的训练方案提供有力支撑。
智能化任务系统在体育训练领域的应用具有重要的实践意义和价值。它不仅提高了教练团队的工作效率和质量,还为学生提供了更加科学、个性化的训练体验。随着技术的不断进步和应用的不断深化,为了进一步提升系统的性能,满足用户多元化的需求,下一步的优化工作将围绕提高成绩预测精度和采用分布式架构来展开。
参考文献:
[1] 刘宇宙,刘艳.Python实战之数据库应用和数据获取 [M].北京:电子工业出版社,2020.
[2] 李小敏.基于用户体验的数字界面文字设计研究 [J].设计,2020,33(6):158-160.
[3] 杨学全.SQL Server实例教程:第4版 [M].北京:电子工业出版社,2020.
[4] 吴广建,章剑林,袁丁.基于K-means的手肘法自动获取K值方法研究 [J].软件,2019,40(5):167-170.
[5] 王建仁,马鑫,段刚龙.改进的K-means聚类k值选择算法 [J].计算机工程与应用,2019,55(8):27-33.
[6] 何晓群,刘文卿.应用回归分析:第5版 [M].北京:中国人民大学出版社,2019.
[7] 赵增炜,刘岭,王文昌.非线性回归的线性拟合加权最小二乘估计 [J].中国医院统计,2008(1):1-2.
[8] 李兵,韩睿,何怡刚,等.改进随机森林算法在电机轴承故障诊断中的应用 [J].中国电机工程学报,2020,40(4):1310-1319+1422.
[9] 李永丽,王浩,金喜子.基于随机森林优化的自组织神经网络算法 [J].吉林大学学报:理学版,2021,59(2):351-358.
[10] 张志刚,徐莹,张锦秋,等.基于随机森林的公路隧道CO气体浓度预测模型 [J].科学技术与工程,2022,22(26):11729-11735.