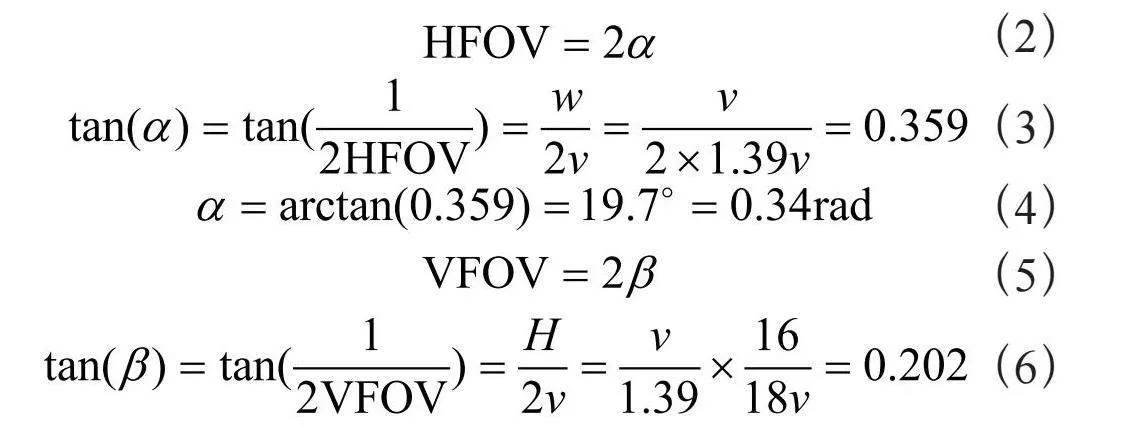
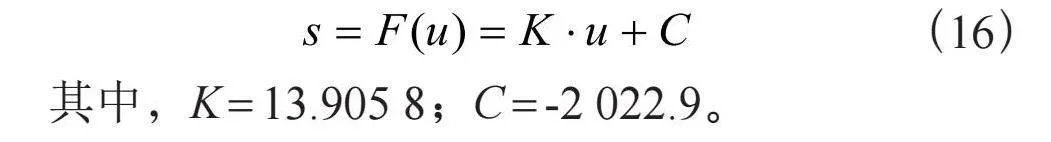



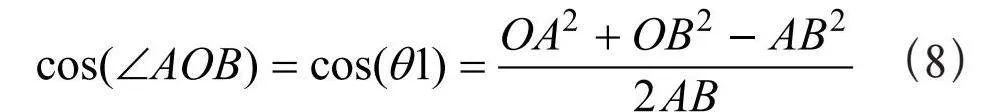
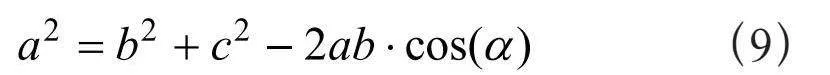

摘" 要:现有投影仪在梯形校正技术中,同时实现翻滚角、俯仰角以及偏航角三个方向下梯形校正需要使用双目摄像头或单目摄像头配合距离传感器以及陀螺仪传感器实现,且产生了成本上升、使用复杂性提升、可靠性降低等问题。现研究一种基于单目摄像头自动梯形矫正方法,实现无须人工干预的全自动图像梯形校正。通过引入几何光学建模,辅助计算投影面上的真实形变四边形投影图像以供投影仪图像校正。实验结果表明,该方法能以低廉的硬件成本,简单的计算方法完成投影仪的自动校正。
关键词:投影机;单目摄像头;几何光学建模;图像处理
中图分类号:TP391.4;TN946.1" 文献标识码:A" 文章编号:2096-4706(2024)23-0042-06
Automatic Correction Method Based on Monocular Camera Projector
ZHANG Enli, YU Yang, ZHANG Zhiqi, YU Congcong
(Shenzhen Skyworth Digital Technology Co., Ltd., Shenzhen" 518057, China)
Abstract: For the existing projector in the trapezoidal correction technology, realizing the trapezoidal correction in the three directions of roll angle, pitch angle and yaw angle simultaneously requires the use of a binocular camera or a monocular camera combined with a distance sensor and a gyroscope sensor. And this leads to problems such as increased costs, increased complexity in use, and reduced reliability. Now, an automatic trapezoidal correction method based on a monocular camera is studied to realize fully automatic image trapezoidal correction without human intervention. By introducing geometrical optical modeling, it assists to calculate the real deformed quadrilateral projection images on the projection plane for the correction of the projector images. The experimental results show that this method can accomplish the automatic correction of the projector with low hardware costs and a simple calculation method.
Keywords: projector; monocular camera; geometric optics modeling; image processing
0" 引" 言
投影作为起源较早的一种显示技术,如今逐渐成为人们学习、娱乐、交流的一种日常工具。随着社会发展和科技的进步,投影仪越来越普及,人们对显示器材设备的需求量越来越大,对其性能、体积、质量、功耗也越来越苛刻。特别是在使用的简洁性方面,反复的手动校正,严重降低消费者的使用意愿。
针对上述问题,陈建峰等[1]提出一种使用单目摄像头、测距传感器模块、三轴加速度模块的组合系统实现投影仪的自动梯度校正,但硬件成本过高;李香兰等[2]提出采用反向畸变处理方法和像素灰度调制方法通过对图像进行预校正实现梯形校正,但是对输出结果最终效果不可控制,无法进行负反馈调节。朱栋等[3]提出通过相机外参求解相机坐标系变换矩阵,构建水平姿态的虚拟相机,建立原图到虚拟相机下的透视映射关系对图像进行校正。李星军等[4]提出基于梯度粒子群的车载雷达图像校正方法,通过多尺度非均匀滤波算法去噪处理,减少噪声烦扰,以图像增益和估算误差优化二阶卡尔曼滤波器参数实现图像校准。
在上述梯形校正方法中对图像处理烦琐,计算复杂度提升,反应速度缓慢,在实际投影仪应用中影响使用效果,增加使用成本。因此提出基于单目摄像头投影仪自动校正方法优势明显。其建立马达位移与像距的关系,为自动梯形校正提供关键参数,可精确分析图像形变并确定梯形形状。采用分步骤校准策略,适应投影仪复杂位置,提高矫正准确性和效率。此外,算法具有较强适应性和扩展性,能满足不同需求并为未来技术改进留有余地。
1" 梯形校正原理
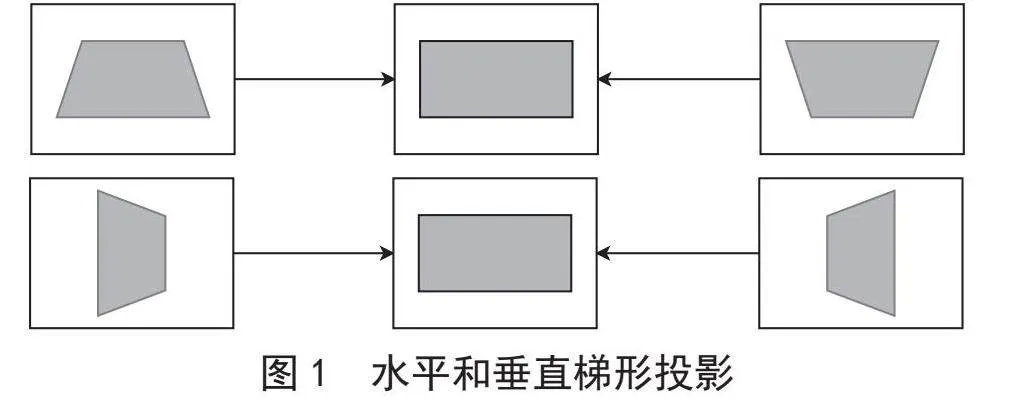
投影仪梯形校正的原理是通过调整投影图像的几何形状,来解决由于投影仪与屏幕之间的角度偏差导致的投影画面变形问题,使其恢复为矩形。当投影仪的光轴与屏幕不垂直时,投影画面会出现梯形失真,即垂直梯形或水平梯形的情况如图1所示。
梯形校正技术主要有以下两种实现方式:
1)光学梯形校正。通过调整投影仪内部的光学元件,如镜头的位置或角度,来改变光线的投射方向,从而在物理上减少梯形失真。这种方法通常需要在投影仪的设计和制造阶段进行考虑,成本较高。
2)数字梯形校正。利用图像处理技术,对投影图像进行数字变换。具体来说,投影仪会检测投影画面的四个角的位置,计算出梯形失真的程度和方向。然后,根据预设的算法,对图像的每个像素进行重新定位和插值计算,以拉伸、压缩或扭曲图像,使其恢复为矩形。
2" 系统总框架
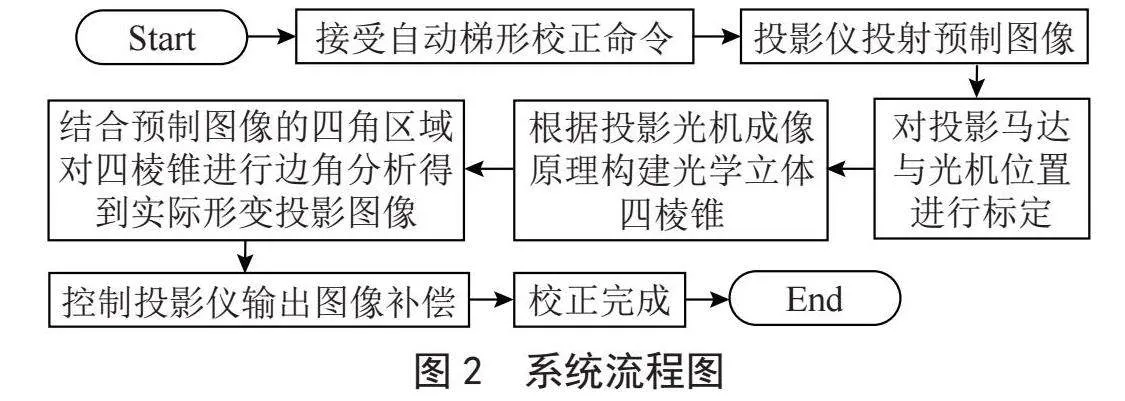
本方法的流程图如图2所示,当接收到自动梯形校正指令,投影仪投射预制图像,摄像头抓取实际投影,识别目标特征点并分区域。对投影仪马达与光机位置进行标定,建立摄像头采集图像与马达移动的联系,通过构建光学立体四棱锥和边角分析计算得到实际形变投影图像,最后控制投影仪输出图像进行补偿来达到矫正目的。
3" 梯形校正算法实现
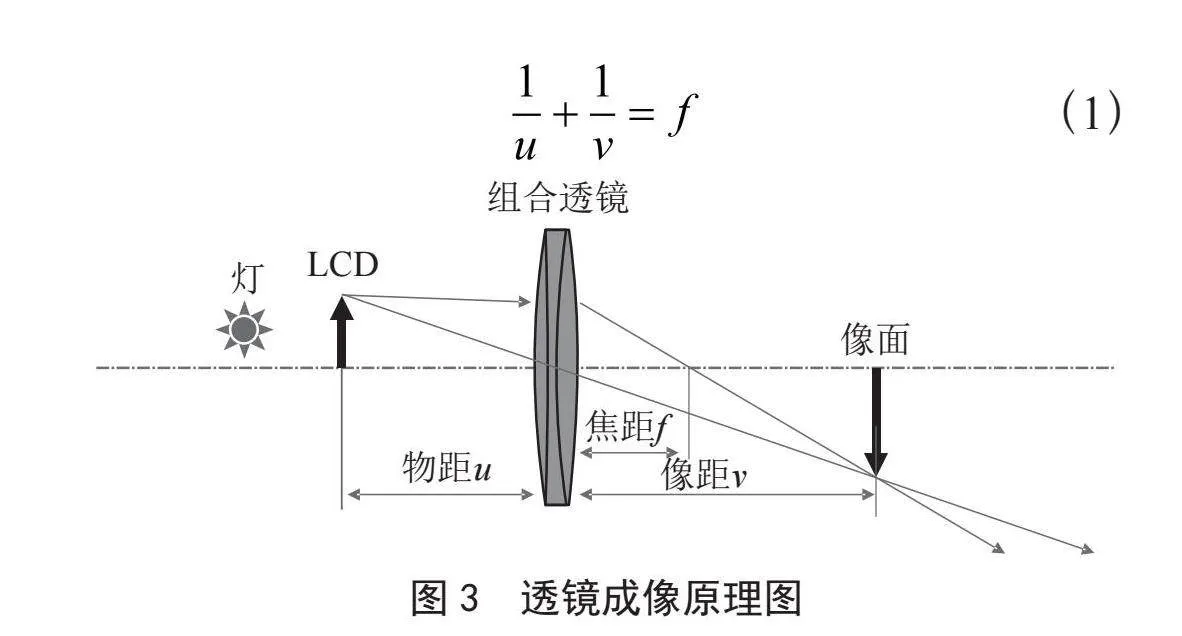
梯形校正算法基于光学成像进行研究。根据单目相机获取投影图像的清晰度确定像距与物距,进而建立投影图像与马达的运动关系。单透镜成像物象关系式如式(1)所示成像原理如图3所示,其中u表示物距,v表示像距,f表示薄透镜的焦距。距透镜u位置放置目标物,通过透镜成像,像面上成像最清晰,其对应距离称为像距v。但投影仪光机镜头非一个单透镜,其由多个单透镜组合而成,因此需要多次光学分析计算确定具体物象关系,进而在图像最清晰时建立投影像距与马达的移动关系。后续算法计算依赖此原理。
(1)
3.1" 初始投影图像标定
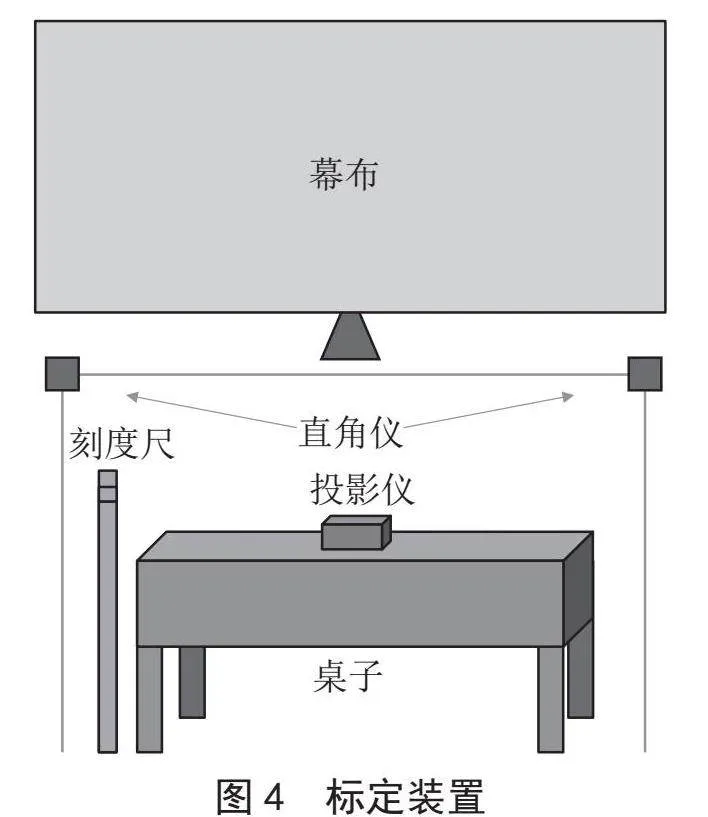
校准工作前需先标定,标定装置如图4所示,先进行投影图像标定,投影仪距墙面一定距离正投影时,对焦使整个像面对焦清晰后,测量投影预制图像中任意直线长度并标记,以实现正投影时初始投影图像校准。每次改变投影仪参数时都需进行初始校准,调整投影仪输出图像,使得投影预制图像中选定直线与标记值相等。初始校准后,用此参数计算水平视场角(Horizontal Field of View, HFOV)、垂直视场角(Vertical Field of View, VFOV)以及四棱锥水平夹角θ1,垂直夹角θ2,经过标定后上述数值将固定不变,参数为后续梯形校正提供计算基础[5]。现简要阐述上述参数计算方法。
3.1.1" 标定计算视场角
设置投影仪于2米处对焦清晰,即像距v为2 m。设投影仪距离与投影宽度比例为1.39,即投射比为1.39。宽高比为16/9。宽度ω = v/1.39,高H =(v/1.39)(9/16)。具体计算式为:
(2)
(3)
(4)
(5)
(6)
(7)
3.1.2" 标定计算光学四棱锥相邻边夹角
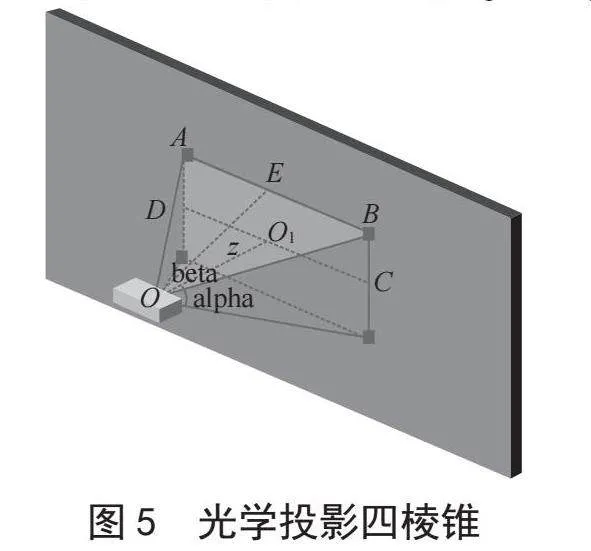
如图5所示的投影光学立体四棱锥中,利用三角关系计算光学四棱锥相邻棱边夹角θ1和θ2。
水平半场角,垂直半视场角,垂直距离为,三角形AOB中的各个边长可过边角关系计算。具体计算式为:
(8)
3.2" 马达位移与像距标定
在正投影标定过程中,像距可通过测量获取,然而物距较难直接得到,而马达移动距离则是可以确定的参数。同时,光机透镜组焦距虽为常数,但在后续参考焦距计算中需要消除其影响。
鉴于此,通过标定来确定像距和马达移动距离的关系就显得尤为重要。在这个过程中,可以利用未知的物距和焦距作为过渡。根据单透镜成像的物象关系如式(1)所示,结合已知和未知参数进行分析。通过多次实验测量不同马达移动距离下的像距,并利用数学方法进行拟合。在拟合过程中,逐步消除物距和焦距的不确定性影响,最终得到像距v和马达s移动距离的具体表达函数v = F(s)。
3.3nbsp; 构建光学立体四棱锥确定梯形形状
在投影仪的正投影初始标定过程中,垂直视场角(VFOV)、水平视场角(HFOV)以及光学四棱锥的相邻两条棱之间的夹角θ1和θ2经计算后在任何时候保持不变。
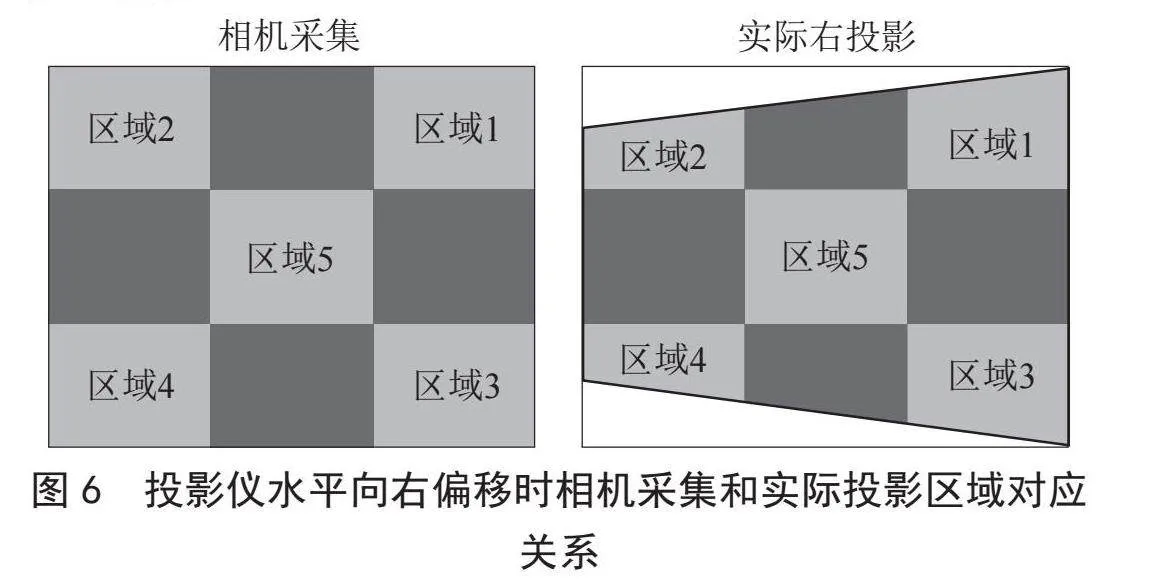
水平偏航角无法直接通过陀螺仪获取,需借助先前标定的像距与马达圈数的关系来确定光学四棱锥的四个棱长。在仅有水平偏航斜投影的情况下,投影形变图像呈现为水平方向的梯形。通过对预处理时分割的四个角的小区域进行对焦,在对焦最清晰时计算出的四个像距即为光学四棱锥的四个棱边长。当已知每两条棱边及其夹角时,利用余弦定理可算出梯形边长,从而确定唯一的水平梯形形状。同时,相机采集的图像与实际投影面的图像呈水平镜像关系。当投影仪向右偏转时,实际投影为左小右大的梯形形状,如图6所示,且选取的区域与相机给出的区域完全成水平镜像。
在向右偏斜投影下,根据马达电机所转圈数与对应像距的关系,当相机拍摄图像的四个角区域最清晰时,分别计算四个角对应的像距的大小,记为v1、v2、v3、v4,此即为光学四棱锥的四条棱长。再次利用三角关系,设光机镜头的光心为A,其对边BC(设为a边)为梯形的一个边长,邻边AC和AB(分别设为b和c)为四棱锥的棱边。依据余弦定理可得到梯形的一个边长a:
(9)
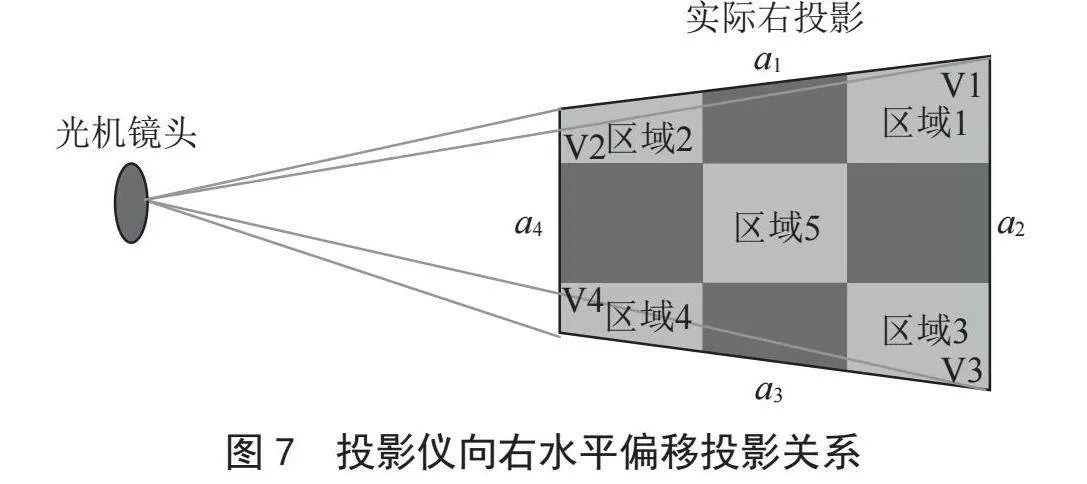
其中a = 0.5HFOV为水平方向的半视场角。当确定一个标准梯形的四个边长a1、a2、a3、a4后,可唯一确定该梯形的形状如图7所示。通过对其进行透射变换,可一次性将梯形形状矫正为矩形形状,反向求出透射变换矩阵,对LCD上显示的图像物象进行变换补偿,使得由LCD投影出去的图像为矫正好的正立矩形图像。
3.4" 全方位自动梯形校正
上述方案能将水平偏移的标准梯形矫正过来。对于投影仪同时存在俯仰角和翻滚角和偏航角情况下,投影到墙面的投影图像不是一个标准水平梯形,按照上述方法计算出四边形的四条边长,无法确定四边形的形状,此时需要陀螺仪测量位姿角辅助计算。
设翻滚角为δ1,俯仰角为δ2,偏航角为δ3,陀螺仪能够准确测得δ1和δ2,因此先对δ1和δ2两个角度形变进行校准。由于偏航角δ3无法由陀螺仪测量,因此偏航角δ3的校准采用清晰度判断像距的方式进行测量。全方位校准时对偏航角的校准应最后进行,故全方位校准步骤顺序为,先校准俯仰角δ2,其次校准翻滚角δ1,最后校准偏航角δ3。
具体操作流程为使用陀螺仪测量δ1和δ2的数值,先根据δ2矫正俯仰角,对原始预制棋盘图像做垂直梯形补偿,再通过仿射变换矫正翻滚角δ1。在翻滚角为δ1和俯仰角为δ2两个方向都校准完毕时,将投影仪输出图像为标记为image1。此时剩下偏航角δ3尚未校准,此时输出图像为一个水平的正梯形投影,根据该正梯形投影进行清晰度判断,进而得到四个角的像距,即可确定梯形的形状,反透射变换得到透射变换矩阵作用于image1上,得到的补偿图像image2通过投影仪输出到墙面即可矫正。
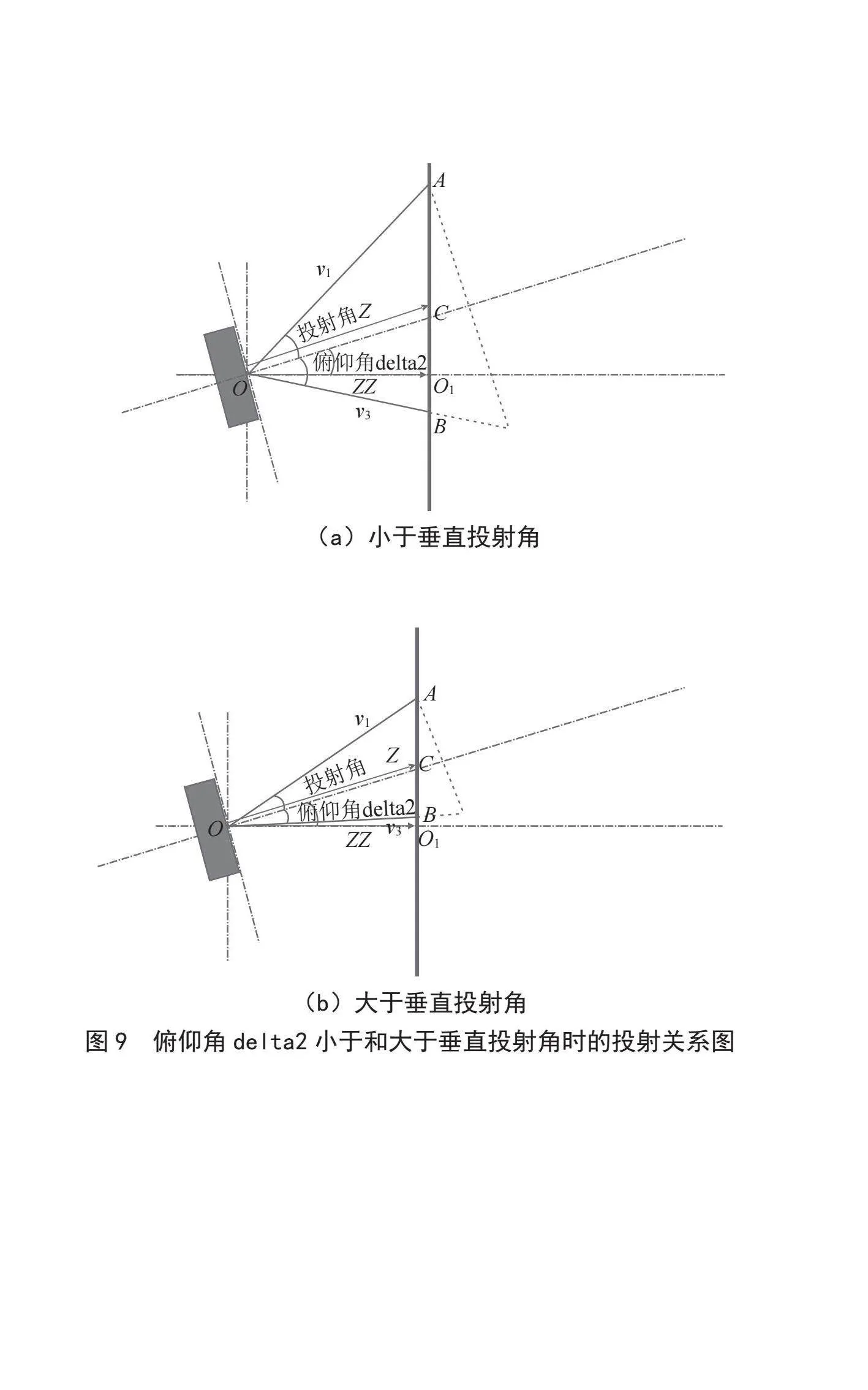
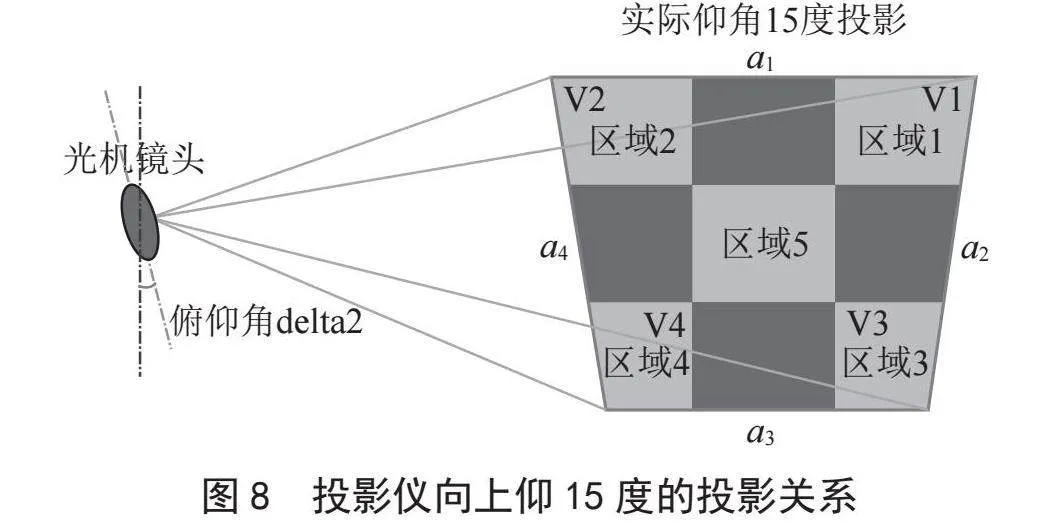
现以俯仰角的校准为例详细讲述矫正过程,设翻滚角δ1和偏航角δ3均为0,只有俯仰角δ2时,其投影图像为垂直正梯形,形状由俯仰角δ2确定。正梯形投影的特点均满足光学立体四棱锥的两两棱长相等。如图8所示为向上仰视情况下的投影视角截面图,将棋盘图像中心区域对焦清晰,记下此处马达所转的圈数,通过标定的物距和像距的关系,计算出此时的像距即为图中的长度Z。通过俯仰角δ2计算出光机镜头中心距离墙面的垂直距离ZZ,通过垂直距离即可计算v1和v3。通过四条棱关系,v1 = v2、v3 = v4,即四条棱长都已知。然后根据4条棱和投射夹角δ1和δ2,通过余弦定理确定梯形的4条边,即确定垂直梯形形状,反透射变换得到透射变换矩阵作用于投影仪输出,即得到投影仪补偿图像,投影仪通过补偿图像输出到墙面矫正。当俯仰角δ2小于垂直半视场角,其投射关系如图9(a)所示。当俯仰角δ2大于垂直半视场角,其投射关系如图9(b)所示。
4" 实验验证
4.1" 初始图像实际标定测试
校准工作之前需要进行标定,现实验环境为投影仪距离幕布2 m并保持投影清晰。
实际标定FOV:设置投影仪在2 m的位置对焦清晰,投影仪距离墙面2 m(2 000 mm)正投影的实测值测得投影高H = 810 mm,宽W = 1 440 mm。理论计算用1.39作为投射比,测得的值W = 2 000/1.39 = 1 438.8(mm),H = (2 000/1.39)(9/16) = 809.35(mm)。实际计算参数如式(10)~(15),对比看出实际值和我们理论计算值基本一致。
(10)
(11)
(12)
(13)
(14)
(15)
4.2" 标定像距v与电机移动距离s测试
在1.4~2.3 m之间做正投影标定,以10 cm为一个单位,由近到远测量10对数据,标定棋盘格中间最清晰时对应的马达电机所转的圈数s和投影仪距离v的关系,通过光学计算和数据分析,得到v和s的表达式。然后斜投影下用v和s的关系计算空间四棱锥的四个棱边,进而确定梯形的具体形状。
为了更加精确,标定阶段采集多组数据,在1.4~3.0 m之间,以10 cm步进测量,采集17对数据,标定棋盘格中间最清晰时对应的马达电机所转的圈数s和投影仪距离v的关系,通过光学计算和数据分析,得到v和s的表达式。为拟合精确,采集2~3组数据,每一组17对数选择2~3组中拟合误差最小的数据作为标定数据:
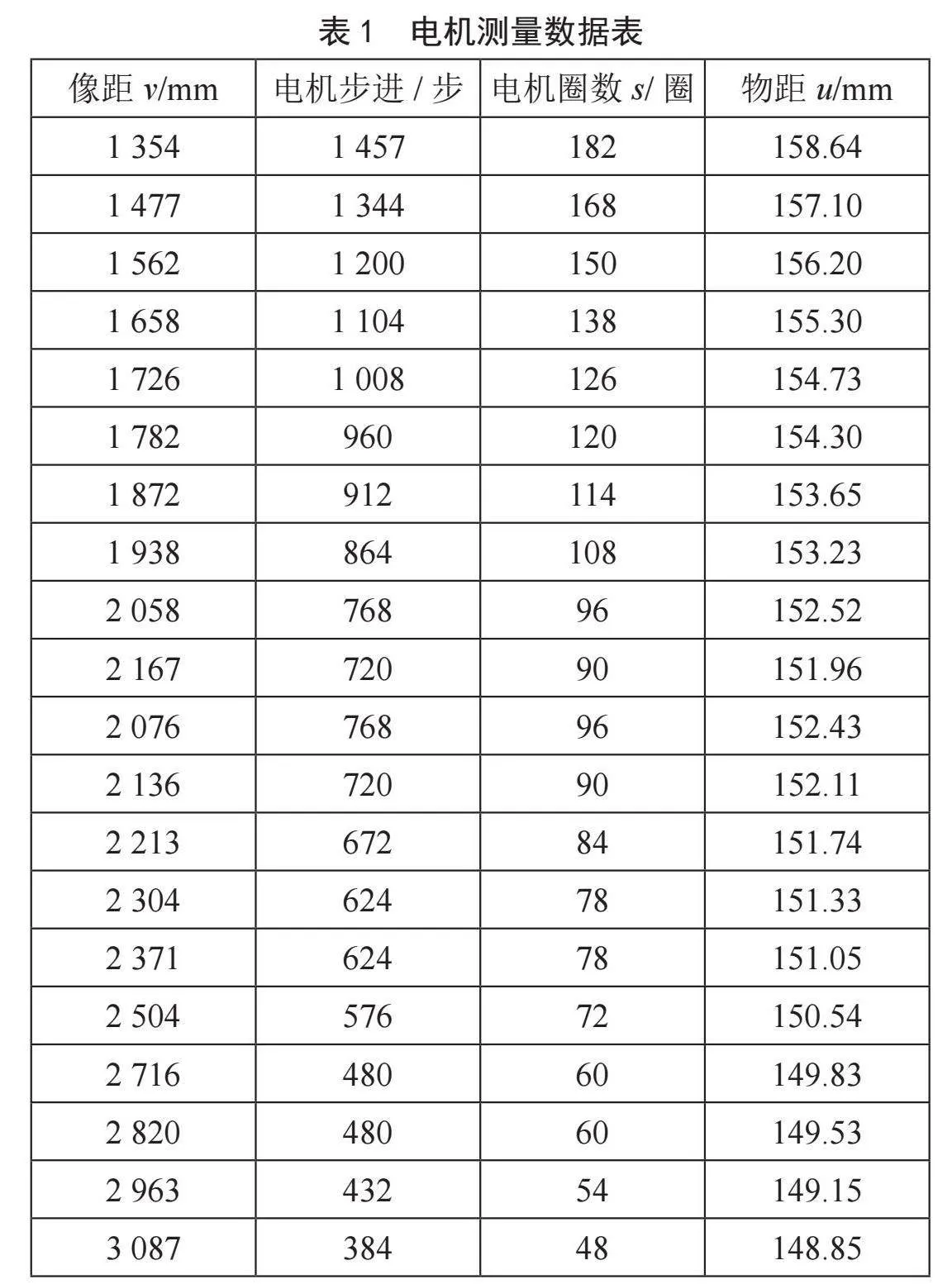
标定数据采集:电机正转,从1.3 m标定到3 m,测量数据如表1所示。
因物距u和电机移动距离s通过物象公式直接求解,而像距v与电机移动距离s无公式进行推导,为了验证像距v和电机移动距离s满足相关性,应用物距u作为中间变量,重新计算物距u与电机s的关系进而推导v与s的关系。通过式(1),将参考f和像距v值代入计算得到一个参考物距u。对以上数据进行拟合。
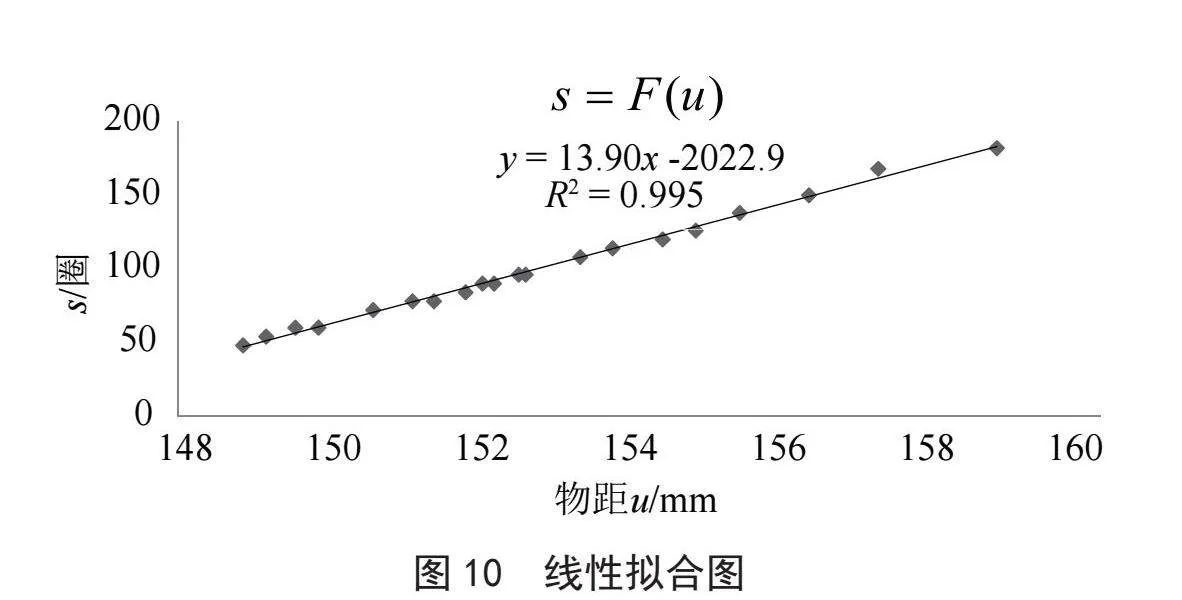
采用加权最小二乘法进行拟合,该方法能够处理异方差问题,提高回归模型的准确性[6]。对测量数据进行描点如图10所示,观察满足线性相关,即采用一元一次方程进行拟合[7],计算出K和C的值,求解线性方程后,需验证方程和数据的相关性,即计算决定系数R2,其主要反映回归模型对因变量的解释程度,随着R2值上升,回归模型对数据的拟合程度越高[8-10]。
(16)
其中,K = 13.905 8;C = -2 022.9。
可以将上述拟合关系的u = F(s)或者s = F(u)与物象关系公式联合起来计算,得到一个关于像距v和马达圈数s的表达关系式。下面将s = F(u) = K1s+C1代入式(1)中,可以得到式(17):
(17)
可见计算出的v和s不是线性关系,任意代入前面测得的(s,v)=(114,1 872),以及K = 13.905 8、
C = -2 022.9两个拟合参数,计算得到此处的f = 142.012 1,带入式(17)可得:
(18)
4.3" 自动梯形校准实际效果测试
将投影仪分别置于俯仰角、翻滚角、水平偏航角三种情况下进行校正测试,校正结果如图11所示。
5" 结" 论
本文围绕投影仪自动梯形校正方法展开,经过深入的探索与分析,取得了以下主要成果:
1)在正投影初始标定中,成功确定了垂直视场角、水平视场角以及光学四棱锥相关参数,为后续的校正工作奠定了基础。通过巧妙地建立像距与马达移动距离的关系,有效地构建了光学立体四棱锥,使得在水平偏航斜投影下能够精准地矫正梯形形状为矩形。这一方法在实际应用中大大提高了投影图像的质量,为用户带来了更好的视觉体验。
2)对于投影仪位姿同时存在俯仰角、翻滚角和偏航角的复杂情况,本研究创新性地提出了按特定顺序进行全方位校准的方法。以俯仰角校准为例进行了详细阐述,通过对焦计算像距、利用俯仰角计算垂直距离,进而确定四棱锥棱长和梯形形状,经反透射变换矫正输出。这一方法不仅具有理论上的合理性,在实际测试中也表现出了较高的准确性和稳定性。
然而,研究也存在一些尚待解决的问题。例如,在实际应用中,陀螺仪的精度可能会受到环境因素的影响,如磁场干扰、温度变化等,这可能会导致位姿检测出现偏差,进而影响自动梯形校正的效果。因此,需要进一步提高陀螺仪的稳定性和准确性,或者探索其他更可靠的位姿检测技术。此外,对于不同型号的投影仪,由于其光学特性和机械结构的差异,可能需要进行个性化的参数标定,这增加了校正工作的复杂性。
未来,可以进一步探索更先进的传感器技术,如激光测距、视觉定位等,提高位姿检测的精度和可靠性。同时,优化算法以提高校正的速度和稳定性,减少计算时间和资源消耗。为了更好地满足用户的需求,可以考虑将该技术与智能投影系统相结合,实现更加自动化和智能化的投影操作,例如自动识别投影环境、自适应调整参数等。
总之,本研究为投影仪自动梯形校正提供了一种有效的方法和思路,为进一步的研究和应用奠定了基础。尽管还存在一些问题需要解决,但相信随着技术的不断进步和创新,投影仪自动梯形校正技术将会越来越成熟和完善,为人们的生活和工作带来更多的便利和乐趣。
参考文献:
[1] 陈健锋,洪坤,郭焰芳,等.便捷式家用投影仪梯形几何校正系统的设计 [J].现代信息科技,2024,8(9):47-52.
[2] 李香兰,金霞,吕金光,等.Micro LED车灯投影光学系统设计与优化 [J].中国光学:中英文,2024,17(1):89-99.
[3] 朱栋,胡伟笑,赵腾.太阳能电池片图像校正与表面缺陷检测 [J].电子测量技术,2024,47(8):126-133.
[4] 李星军,蒋燕翔,邵志伟.基于梯度粒子群的车载雷达图像畸变校正方法 [J].激光杂志,2023,44(10):79-83.
[5] 夏晓华,李玉强,邹易清,等.圆柱曲面透视投影失真的图像校正 [J].光学精密工程,2023,31(11):1691-1699.
[6] 谢明睿,赖纪东,苏建徽,等.一种基于折息最小二乘法的PMSM磁链辨识方法 [J].合肥工业大学学报:自然科学版,2024,47(8):1049-1055+1061.
[7] 陈传玺,陈慧敏,宋韶君.基于最小二乘法的优化GM(1,1)模型及应用 [J].自动化与仪器仪表,2024(8):23-27.
[8] 袁丽,成国坤.基于偏最小二乘法对水库pH值预测与应用 [J].贵州科学,2024,42(4):62-65.
[9] 赖俊霖,王先峰.梯形校正方法、装置、设备及存储介质:CN202410532824.7 [P].2024-08-27.
[10] 高伟,邹学阳,曾建平.一种梯形校正的方法及终端:CN202410841459.8 [P].2024-07-26.
作者简介:张恩利(1979.07—),男,汉族,陕西榆林人,高级工程师,硕士,研究方向:电子信息技术;通信作者:于洋(1983.02—),男,汉族,河北秦皇岛人,高级工程师,本科,研究方向:电子信息技术;张志琪(2002.12—),男,汉族,湖北武汉人,本科,研究方向:电子信息技术;余聪聪(1994.07—),女,汉族,陕西咸阳人,中级工程师,硕士,研究方向:计算光学成像。

