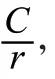
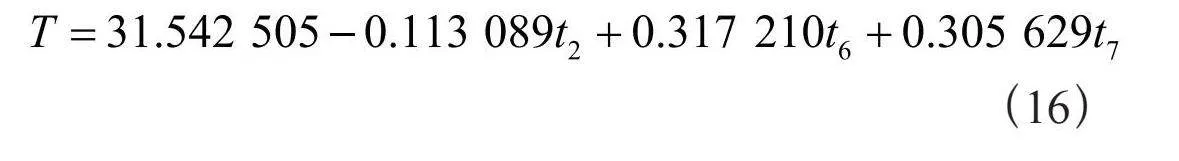
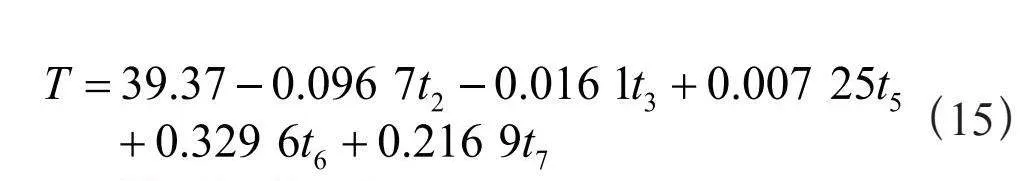





摘" 要:对华南农业大学电子工程学院电子信息工程专业三个年级进行了学情分析及学业预警的研究。使用MATLAB R2021a和SPSS软件,采用综合评价、多元线性逐步回归、决策树三种不同的建模方法对某科目是否及格进行预测。对一组学生数据分别用三种模型预测数字电子技术课程成绩,对比其预出率和预错率,通过模型集成,建立不及格等级制模型量化预测结果。依据预测结果做出合理干预,从而达到预防学生挂科的目的。
关键词:学情分析;学业预警;综合评价;逐步回归;决策树
中图分类号:TP311" 文献标识码:A" 文章编号:2096-4706(2024)23-0153-06
Academic Situation Analysis and Academic Early Warning Based on Model Integration
YIN Huili, LIU Wentao, LI Jianyu, RAO Junhua, LI Lishan
(College of Electronic Engineering and College of Artificial Intelligence, South China Agricultural University, Guangzhou" 510642, China)
Abstract: This paper conducts research on academic situation analysis and academic early warning for three grades of electronic information engineering major in college of electronic engineering of South China Agricultural University. It uses MATLAB R2021a and SPSS softwares, and uses three different modeling methods, including comprehensive appraisal, multiple linear stepwise regression, and Decision Tree, to predict whether a subject passes. For a group of student data, three models are used to predict the results of the digital electronic technology course, compare the pre-output rate and pre-error rate, and establish the failed hierarchical model to quantize prediction results through model integration. According to the prediction results, this paper makes reasonable intervention, so as to achieve the purpose of preventing students from failing.
Keywords: academic situation analysis; academic early warning; comprehensive appraisal; stepwise regression; Decision Tree
0" 引" 言
传统的高等教育侧重于以知识传授为主导的智育教育[1]。高质量发展是新时代的硬道理,全面贯彻新发展理念是高等教育发展的新动力,然而在当代社会的飞速发展和国家民族振兴的关键需求下,发展新质生产力,需要培养更多具备综合素质和创新能力的人才,因此,为高等教育赋予了新的使命[2]。在这样的时代背景下,学业预警制度的完善与改进也越来越重要。
学业预警制度是指高校以对学生学习过程监控为出发点,构建起一套日常学习、生活等多元一体的学业预先警示工作系统,针对学生学业方面存在的问题和困难,通过学校、家长与学生之间的多方沟通与协作,给予及时干预,帮助学生更好地完成学业[3]。
本研究选取数字电子技术作为分析预警的课程,基于模型集成对学生电类课程的学情进行分析,并对数字电子技术课程期末考试的合格率进行预测,依据预测结果对学生学业状况预警。分析过程中所收集的数据包括高等数学、电路、模拟电子技术、数字电子技术等科目小测成绩、期末成绩、学生某学年年级排名、缺勤次数、挂科数量等。
采用三种不同的方法建立预测模型。其中综合评价预测模型则选取收集到的数据作为评价指标,对学生个人的该科目学业情况进行评分,根据评分预测该学生是否合格。多元线性回归预测模型是将学生该科目期末成绩作为因变量,使用逐步回归方法建立多元线性回归模型预测学生该科目成绩。第三种决策树分类预测模型通过构建决策树,将学生分为合格与不合格两类,达成对学生该科成绩是否合格的预测。分别使用三种模型,对同一组数据进行预测,对比三种模型的预出率(预测出确实不合格人数占总不合格人数的比例)和预错率(预测出但实际成绩合格的人数占预测出的总人数的比例),分析模型优劣。最后将三种模型按预测结果进行模型集成,建立不及格等级制模型的预测机制,优化预测效果。
1" 综合评价预测模型
1.1" 评价指标选取与指标正向化
1.1.1" 相关性分析
将数电成绩,即待预测科目的成绩作为因变量,将学生其他评价指标作为自变量,计算两变量(定距变量、定比变量)Pearson相关系数。其表达式如式(1)所示:
(1)
其中,Xi表示学生其他评价指标,Yi表示数电成绩,r表示求得的Pearson相关系数。
1.1.2" 评价指标选取
分析因变量数电成绩T(学生待预测的电子类科目成绩,即及格与不及格)与自变量大一上学期学情排名t1、大一下学期排名t2、大二上学期排名t3、小测成绩t4、高数成绩t5、模电成绩t6、电路成绩t7、大物成绩t8、缺勤次数t9、上一学期挂科数量t10、大一下与大二上学期相比的排名进步名次t11之间的皮尔逊相关系数。
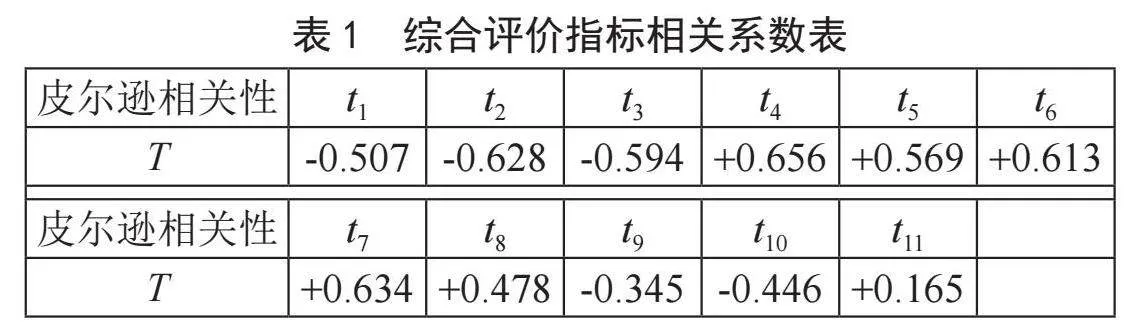
通过SPSS对搜集到的数据进行相关分析[4],得到如表1所示的相关系数表。
分析表1可知,因变量数电成绩T与自变量大一下学期排名t2、大二上学期排名t3成强负相关,与自变量小测成绩t4、模电成绩t6、电路成绩t7成强正相关。选取该五个自变量作为评价指标。
1.1.3" 指标正向化
将选出的五个指标类型转化为极大型指标。小测成绩t4、模电成绩t6、电路成绩t7本身为极大型指标无须转化。自变量大一下学期排名t2、大二上学期排名t3为极小型指标,转化为极大型指标计算式(2):
(2)
其中,max表示t2、t3中最大值,x表示t2、t3,t表示正向化后指标。
1.2" 基于TOPSIS的综合评价
1.2.1" TOPSIS优劣解距离法
TOPSIS优劣解距离法是一种多属性决策分析方法,用于确定最佳方案[5]。
假设被评价对象有m个,每个被评价对象的评价指标有n个,构建式(3)所示判断矩阵:
(3)
对判断矩阵根据式(4)进行标准化处理:
(4)
分别根据式(5)和式(6)确定最优解和最劣解:
(5)
(6)
根据式(7)和式(8)计算各方案与最优解和最劣解的欧式距离:
(7)
(8)
根据式(9)计算综合评价指数:
(9)
其中,Ci值越大代表评价对象越优。
1.2.2" 综合评价模型建立
根据式(10)得到线性加权函数[6]:
(10)
其中,Wij表示权重且所有权重视为相等。
利用MATLAB R2021a软件建模,得到综合评价模型,对m个学生的该科成绩进行综合评价,根据评价结果对学生该科是否合格进行预测。
1.3" 预测结果
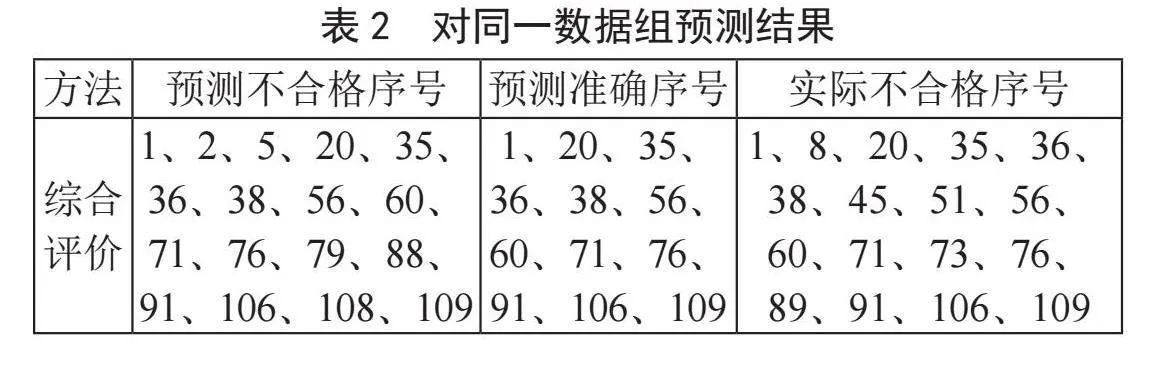
假设已知有x人不合格的情况下(数电期末成绩小于等于60都归于不及格),按综合评价的分数高低,取出其中的评价分数倒数的x人。在收集到的数据组中,对120名学生的数电成绩进行预测,预测结果如表2所示。
2" 多元线性逐步回归预测模型
2.1" 回归步骤
2.1.1" 方差齐性检验
由前面的相关性分析可知,相关性大于0.55的各学生学业指标(t2、t3、t5、t6、t7,小测成绩t4由于数据缺失弃用)与数电成绩有较强的线性关系,因此构建多元线性回归模型对学生数电成绩进行预测[7],从而预测学生数电成绩是否及格。线性回归前需要先对数据进行方差齐性检验[8]。
通过SPSS软件进行基于中位数并具有调整后自由度的方差分析,得到如表3所示的方差齐次检验表。
由于表3中的显著性均大于0.05,因此可以认为方差齐性检验通过,可以进一步进行线性回归建模工作。
2.1.2 建立多元线性回归模型
多元线性回归分析的模型如式(11)和式(12)所示:
(11)
(12)
其中,β0,β1,…,βm表示偏回归系数,与x1,x2,…,xm无相关性。ε表示随机误差项。
假设,因变量与各自变量之间存在线性关系,两者之间的线性总体回归模型可以表示为式(13)和式(14):
(13)
(14)
式(13)和式(14)中,ε表示随机误差项。
2.1.3" 求解回归系数
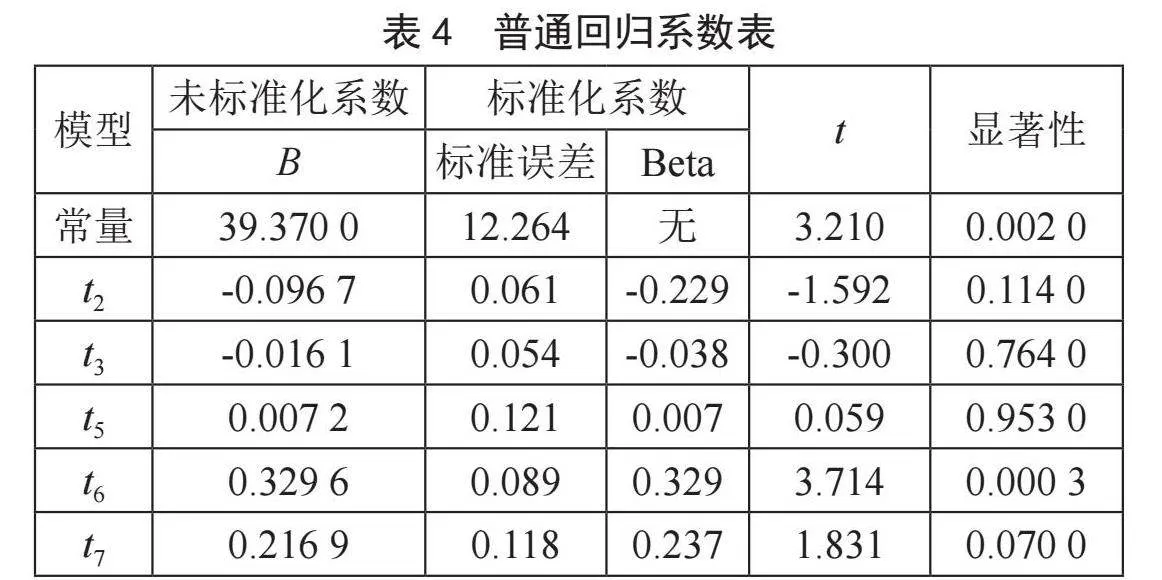
利用SPSS建立普通线性回归模型得到回归系数如表4所示。
最终得到的多元线性回归方程可表示为式(15):
(15)
2.1.4" 模型误差分析
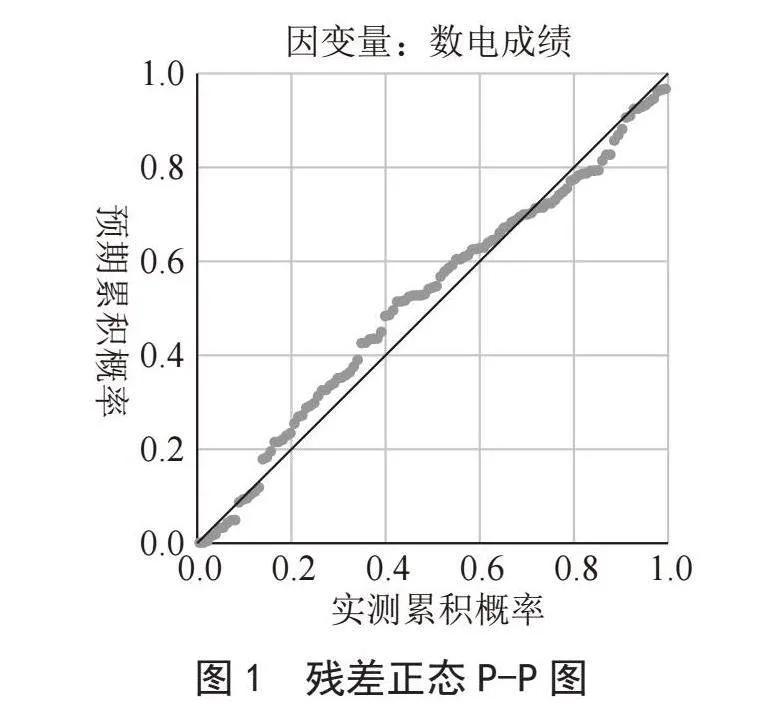
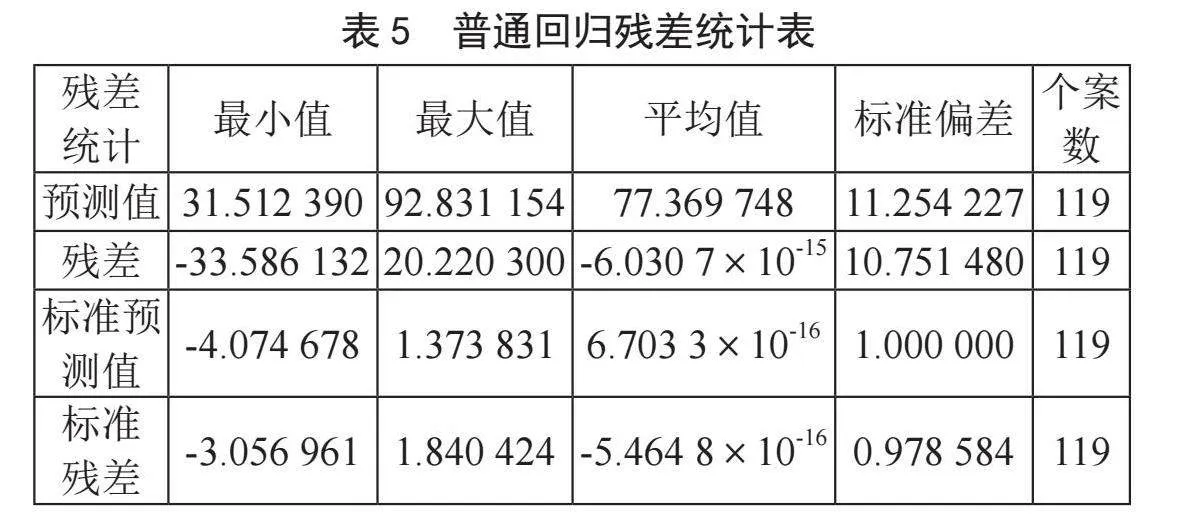
利用SPSS计算出了模型的相关系数R = 0.723和决定系数R2 = 0.523,模型残差如表5所示,回归标准化残差的正态性验证如图1所示。
由表5和图1所得的残差正态P-P可以得出,其残差最大值分别为20左右,其标准化残差分布都在直线附近,可以认为标准化残差满足正态分布,误差通过,建立的回归方程合理,且误差较小。
2.2" 逐步回归分析
建立的多元线性模型中将相关性一般的变量也建立了进去,因此我们考虑将相关性一般,显著性不足的变量剔除,建立最优多元线性回归方程[9]。
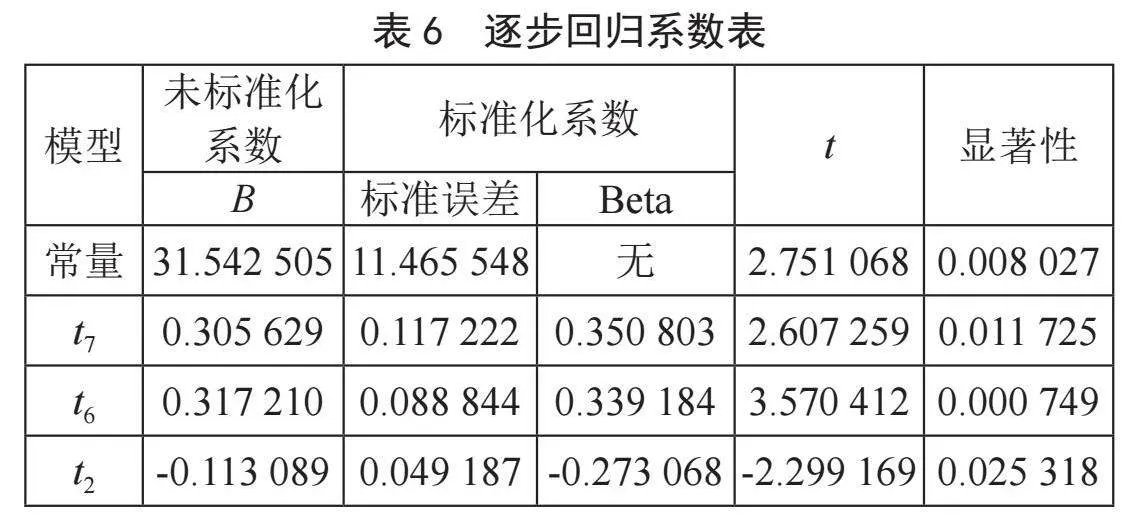
通过SPSS完成对逐步回归模型的求解,得到如表6所示的逐步回归系数表。
最终得到的多元线性回归方程可表示为:
(16)
利用SPSS计算出了模型的相关系数R = 0.853和决定系数R2 = 0.727。
普通回归模型决定系数R2 = 0.523,逐步回归模型决定系数R2 = 0.727。逐步回归模型拟合度更高,用该模型进行学情预测更合适。
2.3" 预测结果
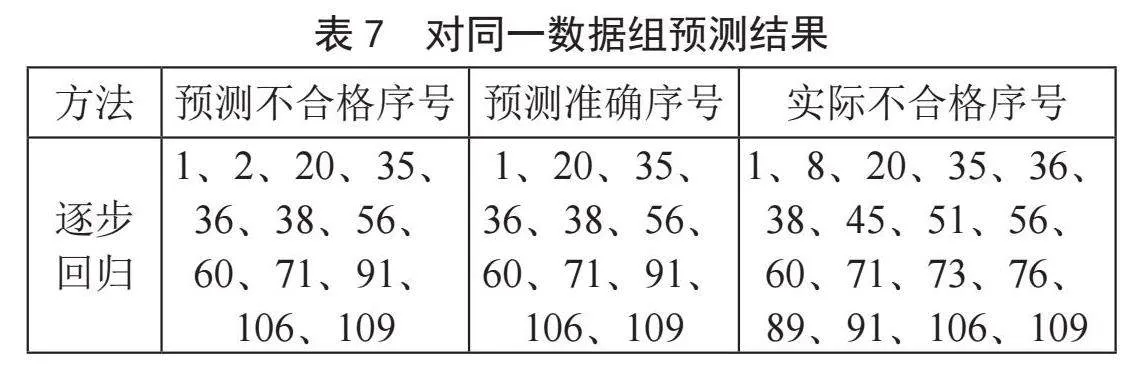
在收集到的数据组中,采用逐步回归模型对120名学生的数电成绩进行学情预测,预测结果如表7所示。
3" 决策树分类预测模型
3.1" 决策树算法
决策树是一类机器学习算法,因其结构形似一棵树而得名[10]。决策树是一种常用于数据挖掘的机器学习算法,它以树形结构表示决策过程,可用于分类和回归任务。通过反复递归选择最优特征对数据集进行分割,使最终划分的子数据集达到想要的分类结果,具有模型可视化程度高,易于理解以及时间复杂度小等特点[11]。常见的决策树算法包括ID3、C4.5、CART等。决策树学习过程包括特征选择和决策树生成,以及决策树剪枝[12]。在构建决策树模型时,使用MATLAB R2021a软件,并通过导入相关数据进行模型训练,最终采用MATLAB R2021a中的ClassificationTree.fit()函数构建ID3算法决策树模型。
3.2" 决策树构建
3.2.1" 导入数据
将全部530名学生进行随机分组,抽取300名学生数据作为训练集,剩下230名学生数据作为测试集。其中的学生数据有该学生高等数学AII成绩X1、大学物理A成绩X2、电路成绩X3、模拟电子技术成绩X4、大一上学期到大二上学期三学期加权绩点排名平均值百分比X5、不及格科目门数X6。
3.2.2" 构建决策树模型
通过MATLAB R2021a自带的ClassificationTree.plot() 函数绘制和可视化决策树模型的结构和结果,决策树根节点0表示不及格,1表示及格。生成的决策树模型如图2所示。
3.2.3" 优化决策树
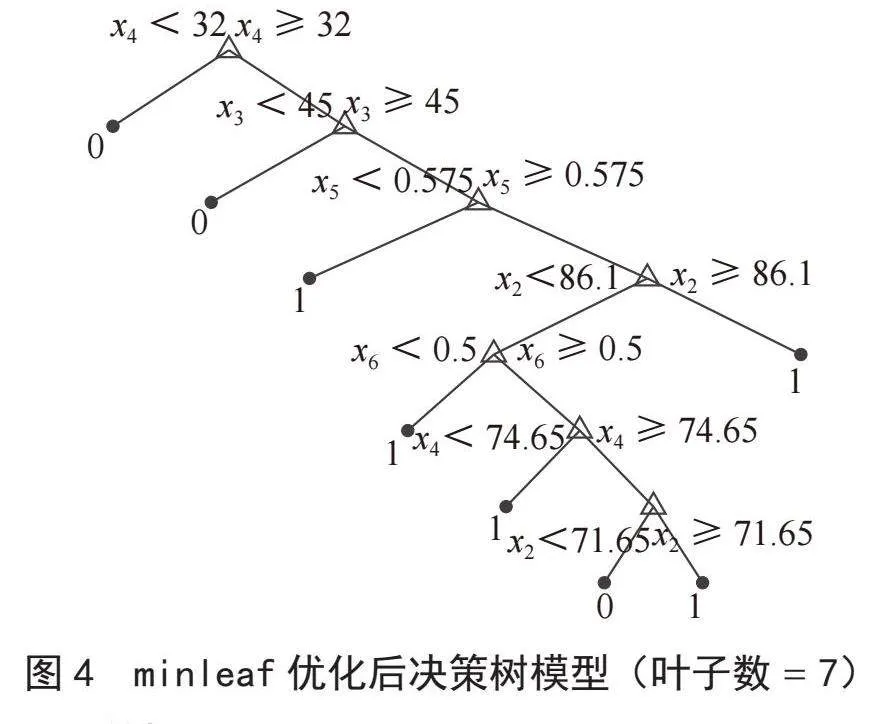
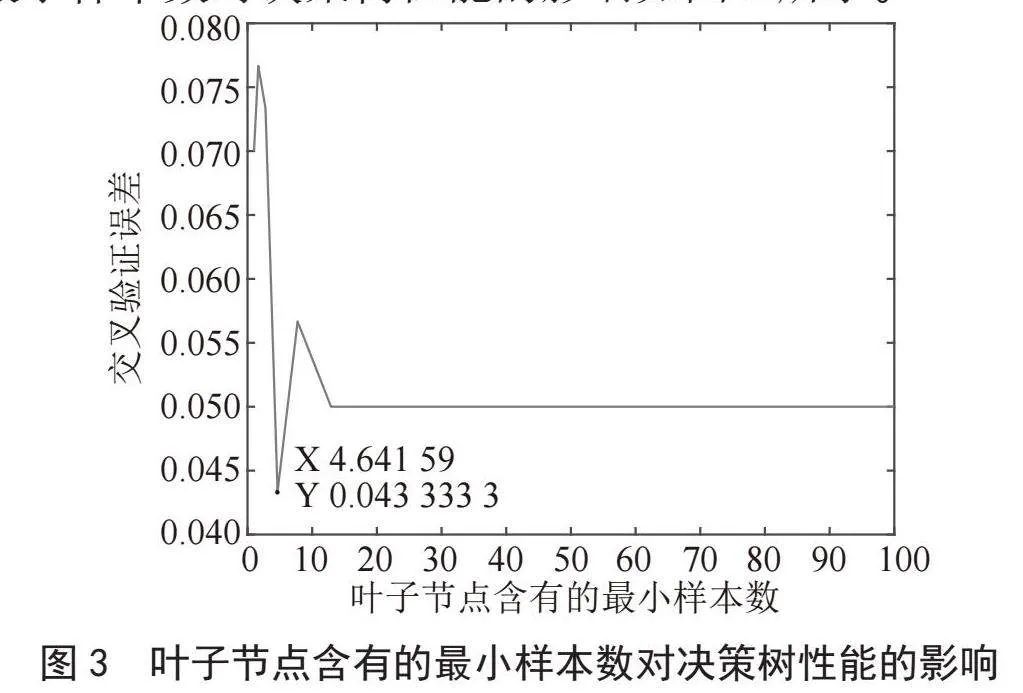
对构建好的决策树进行预处理,通过设置叶子节点最小样本数来提升决策树的性能。叶子节点含有的最小样本数对决策树性能的影响如图3所示。
根据图4以及对多种叶子节点含有的最小样本数进行试验,最终选择minleaf为4对决策树进行构建。优化后的决策树模型如图4所示。
3.3" 预测结果
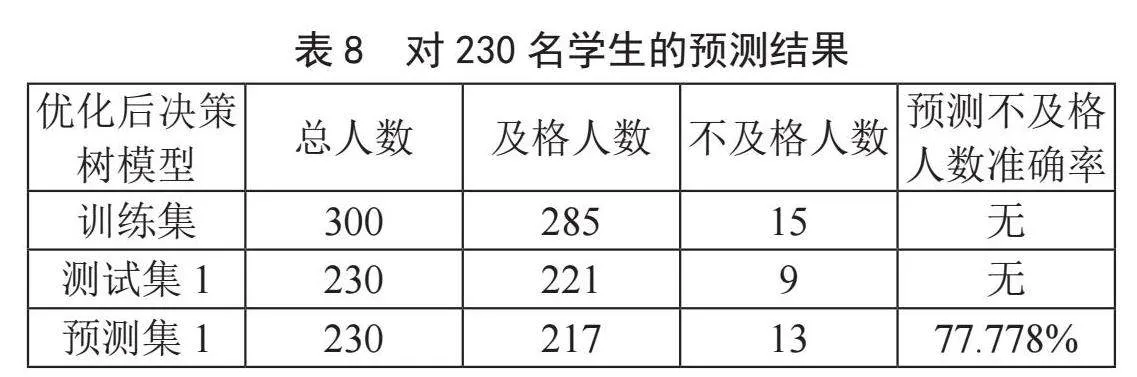
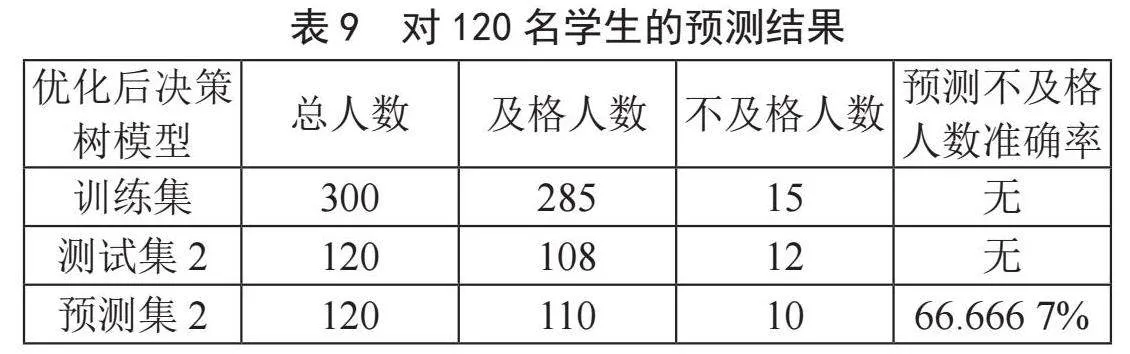
对随机抽取的230名学生数电成绩及格情况和准确率的预测结果如表8所示,对2021级120名学生数电成绩及格情况和准确率的预测结果如表9所示,将预测结果与实际结果进行对比分析,从而得出决策树模型预测的准确率。
4" 模型集成
4.1" 各模型优劣分析
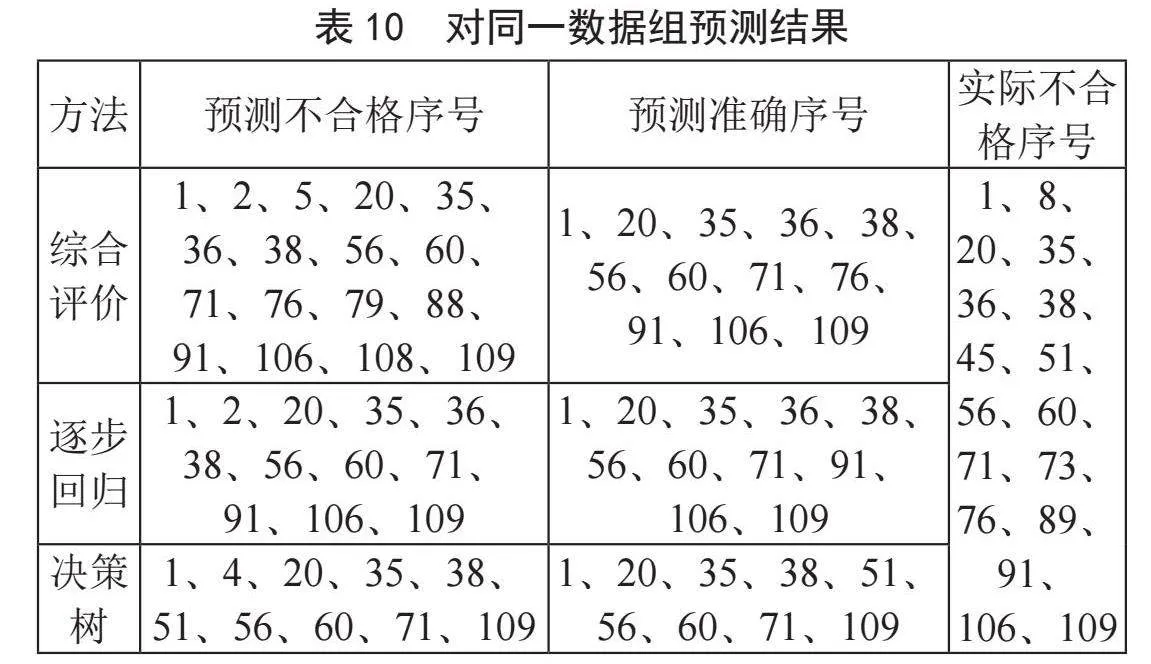
使用上述三个模型对华南农业大学120名学生样本的数电成绩是否及格进行预测,预测结果如表10所示。
综合评价预测模型在假设已知不及格人数条件下不及格学生预出率(预测出确实不合格人数比总不合格人数)和预错率(预测出但实际合格人数比预测出的总人数)分别为70.59%和29.4%,多元线性逐步回归预测模型在无须已知不及格人数条件下不及格学生预出率和预错率分别为64.7%和8.33%,决策树分类预测模型在无须已知不及格人数条件下不及格学生预出率和预错率分别为53%和10%。
由上述分析可以得出:
1)综合评价预测模型在对任意一组陌生数据预测时,预测的预出率高,但这是建立在假设不及格人数已知的条件下,而且其预测错误率较高,容易对学习成绩不差的同学产生不及格误判。
2)多元线性逐步回归预测模型对改组数据预测时,预测的预出率较高,但这组数据属于构成该逐步回归模型的拟合集,预出率有虚高风险,不过其预测错误率较低,不易产生不及格误判。
3)决策树分类预测模型对任意一组陌生数据预测时,预出率一般,但预测错误率低。其预出率一般是由于各年学生数据训练集间的数据有较显著差异,导致模型训练效果不好,多元线性逐步回归模型也会受到影响,因此要建立适用的学情预测模型,需使用待预测学校学院专业自身的各年数据作为训练集,不过综合评价预测模型有已知不及格人数条件修正受此影响小。
4.2" 基于模型集成的不及格等级制模型
为了降低模型预错率,将三种模型按预测结果集成,把三种模型预测出的不及格序号叠加,某个序号在三个模型中的一个出现时,认为是一级不及格学生;出现在两个模型中时,认为是二级不及格学生;出现在三个模型中时,认为是三级不及格学生。
三级不及格学生有1、20、35、38、56、60、71、109,其中确实全为不及格。二级不及格学生有2、36、91、106,其中只有序号2一个误判。一级不及格学生有4、51、76、79、88、108,其中51、76确实为不及格。
级别代表可信度,当为三级不及格学生时,该学生一定不及格;当为二级不及格学生时,四分之三的概率不及格;当为一级不及格学生时,三分之一的概率不及格。可以通过先分析收集到的数据,结合自身学校实际情况,判断收集到的数据是否与实际情况有较大差别,若有较大差别,一到三级的学生都纳入预警的范围,若收集到的数据与实际相符,就仅将二到三级的学生纳入预警范围。模型集成的不及格等级制模型大大降低模型预错率,也提高了预警效率。
5" 结" 论
在使用同一组学生数据预测数电成绩时,综合评价预测模型在假设已知不及格人数条件下,不及格学生预出率和预错率分别为70.59%和29.4%,多元线性逐步回归预测模型在无须已知不及格人数条件下,不及格学生预出率和预错率分别为64.7%和8.33%,决策树分类预测模型在无须已知不及格人数条件下,不及格学生预出率和预错率分别为53%和10%。使用二级的不及格等级制模型,在无须已知不及格人数条件下,不及格学生预出率和预错率分别为64.7%和8.33%。受不同年份学生学科数据波动影响,模型在预测学生不及格预出率效果一般,但模型在得出预测结果的过程中能产生学生该学科成绩排位,依据此排位能对学生不及格预警产生较好的效果。
对数电不及格预测的结果发现:数电成绩与大一下学期、大二上学期的学生绩点排名、电路、模电成绩有强正相关性。在使用集成后二级不及格等级制模型预测时,未被预测出不及格的学生,各学期排名和相关学科成绩并不差,出现不及格情况大多是由于考试状态不佳或者对该科目的学习状态出现了急剧下滑。实际及格但是被误测的学生,前面学期排名或相关学科成绩都十分一般,但对本学期该科的学习比较重视或是学习状态有所改善。
参考文献:
[1] 李晓虹,张婷婷,王梓宁,等.我国高等教育数字化转型建设路径的定性比较分析 [J].远程教育杂志,2024,42(1):32-40.
[2] 范佳洋.高等教育高质量发展的宪法叙事:规范阐释与实现路径 [J].北京理工大学学报:社会科学版,2023,25(3):179-188.
[3] 郭连生,柳贝贝.高等教育背景下大学生学业预警机制的构建与研究 [J].未来与发展,2022,46(2):64-71.
[4] 曾凡金,杨勇,冯春杰,等.“国考”成绩与学业成绩相关性分析及教学建议——以物理学科知识与教学能力科目成绩为例 [J].高教学刊,2024,10(7):89-92+97.
[5] 杜挺,谢贤健,梁海艳,等.基于熵权TOPSIS和GIS的重庆市县域经济综合评价及空间分析 [J].经济地理,2014,34(6):40-47.
[6] 张娟,许志勇.综合评价法在教学质量评价中的应用 [J].统计理论与实践,2022(8):68-72.
[7] 李小鸭,张娜,邹颖.应用型本科高校教与学过程对大学生就业力影响因素的研究——基于线性回归及结构方程模型 [J].陕西教育:高教,2022(10):76-77.
[8] 刘炯.基于多元线性回归的物流需求预测分析——以安徽省为例 [J].四川文理学院学报,2022,32(2):51-58.
[9] 张静静,马林转,张运瀚,等.基于逐步回归法对钢铁企业球团工序二氧化硫的影响因素分析 [J].云南民族大学学报:自然科学版,2023(3):1-7.
[10] 王辉,张文杰,刘杰,等.基于分类回归决策树算法的航班延误预测模型 [J].中国民航大学学报,2022,40(3):35-40.
[11] 姚亮,周晏.基于决策树算法的地灾数据可用性分类研究 [J].信息技术与信息化,2023(6):44-47.
[12] 杨小娟.决策树算法在学生课程成绩分析中的应用研究 [D].昆明:云南师范大学,2021.
作者简介:殷惠莉(1975—),女,汉族,山东东营人,讲师,硕士,研究方向:电子技术、农业信息化;刘文韬(2003—),男,汉族,湖南益阳人,本科在读,研究方向:电子信息工程;李健羽(2002—),男,汉族,广东云浮人,本科在读,研究方向:电子信息工程;饶俊华(2003—),男,汉族,广东广州人,本科在读,研究方向:电子信息工程;李丽珊(2003—),女,汉族,广东清远人,本科在读,研究方向:电子信息工程。